重力加速度在空間中有一個分佈變化

重力

萬有引力是第一個被研究的超距力

 

萬有引力公式

f = G M m / r²
以上為力的大小，方向則為吸引力

重力場

「場」在物理中指的是空間的函數，重力加速度在空間中有一個分佈變化的情形，在空間中的任一點都受重力影響，因此可以說地球重力的效應對其附近有質量的物質形成了重力場。

基本數學技能及重要結論

與距離平方成反比的作用力，作用源（在此是質量）是均勻球殼分佈，則對
(1) 球殼外空間中一個點之力的作用，等效於球殼之作用源全部集中在球心那一點上。
(2) 球殼內空間中一個點之力的作用，合力為零
本節重點：如何作球殼的引力積分

距地心不同遠近的重力大小

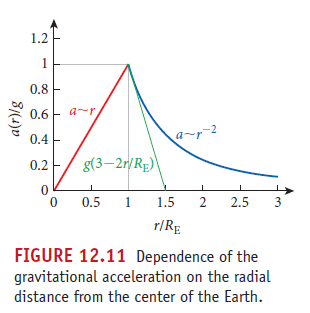
假設地球為一均勻質地的理想球體，則透過積分可得知距地心不同遠近處之重力加速度

地表附近的重力場（重力加速度）

對於一般日常物品，地球非常巨大，在人類日常居住及活動的範圍，引力也無變化，因此可視為常數。
 

在地表上空幾百公里範圍內，可合理地線性近似為

g(3 - 2r/R)
其中 r 是與地心距離、R 是地球半徑

地球內部的重力場

線性遞減至地心處為無重力
 

地球的質量是如何量到的？

卡文迪西 (Lord Cavendish)

 

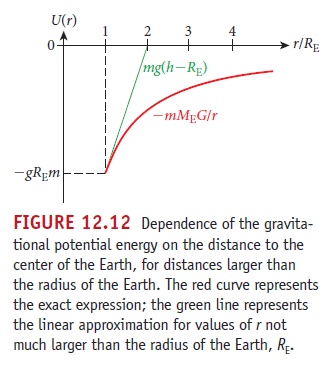
星球的重力位能

脫離速度

系統總力學能

E = 1/2 mv₁² + 1/2 m v₂² - G m₁ m₂ / |r₁ - r₂|
從地球質心的座標來看，上式成為
E = 1/2 m v² - G M m / (R+ h)
上式為零的條件是
v = √(2GM/R)
 

Example 12.3 Asteroid (小行星) 撞擊 之動能計算
 

重力拋射 (Gravitational Sling-shot) 或 重力協助 (Gravitation Assist)

探測衛星用來獲取額外動能的方法
見圖 12.3 (p.394)
（這樣是不是能量的路無中生有？）

 

 

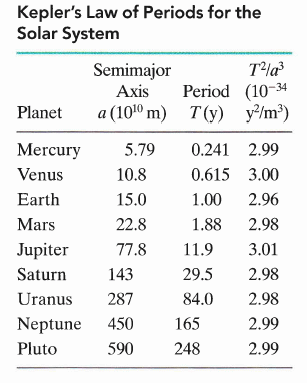
經典議題：克卜勒三大行星定律

在牛頓之前，來自其老師之大量觀測值而獲得的歸納，可完全由牛頓運動定律推得
那為什麼還要認識它？（因為它是很簡明有用的規則整理，不容易直接由牛頓定律推得）
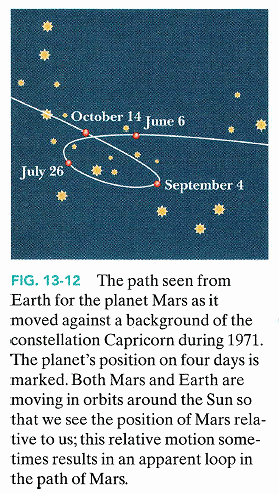
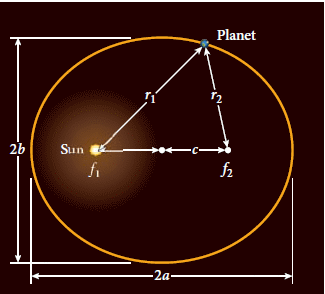
第一定律：軌道

行星軌道為橢圓

第二定律：面積

掃過面積之速率相等（即遠處繞得慢，近處繞得快）

第三定律：週期

T² / a³ = 常數 （事實上=  4π² / (GM) ）

由於正圓也是橢圓之一特例，故滿足該定律，課文示範了第二、三兩定律在正圓軌道時的推導
以其簡明單純，克卜勒行星定律深深支持地動說（太陽中心論）
例題B SP 12.1：冥外行星周期之預測
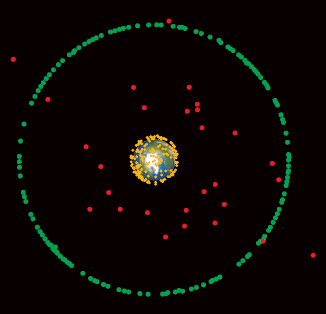
例題 B 12.4：銀河中心處的黑洞
 

克卜勒第二行星定律來自角動量守恆

課本證明
故克卜勒第二行星定律與滑冰選手快速自轉有相同的原理
 

衛星軌道

電視衛星（綠點）對地上居民而言永遠定在天空的同一點，因此它的軌道只能是固定的 5.61 倍地球半徑，且位在赤道正上方（為什麼？）
例題 Solved Problem 12.2：衛星飛行速率
例題 Solved Problem 12.3：小耳朵衛星天線調整
5.61 倍地球半徑是怎樣求出來的？（可利用第三行星定律）
 

衛星的動能與位能

推導維持軌道所需之速度，可得一通則
K = -1/2 U
 

黑暗物質與黑暗能量

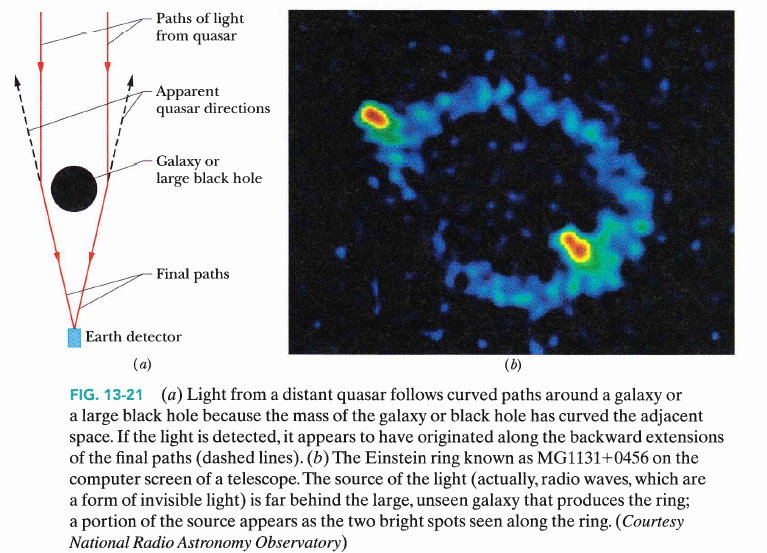
根據軌道運動推算，星系（如銀河系、仙女座）的質量比天文觀測到的大三到五倍
近幾年的新觀測甚至看到無法解測的能量注入促成宇宙加速膨脹，因而宇宙中可能尚有人類不知道的能量形式或來源
 

廣義相對論與重力

等效原理

因運動而加速與受重力場影響而加速是分不出來的。

空間的彎曲

定義距離的方式加以推廣後,，就可以有彎曲的空間了。
距離（測度）的廣義定義：

x, y, z 是任意三個點，d 為一恆正的實數值函數
d(x,x) = 0
d(x,y) = d(y,x)
d(x,z) < = d(x,y) + d(y,z)