isomorphismes
shapes, figures, and forms.
Posted on Wednesday, 8 August 2012
Just playing with


on WolframAlpha. That’s Wikipedia’s example of a function with two poles (= two singularities = two infinities). Notice how “boring” line-only pictures are compared to the the 3-D ℂ→>ℝ picture of the mapping (the one with the poles=holes). That’s why mathematicians say ℂ uncovers more of “what’s really going on”.
As opposed to normal differentiability, ℂ-differentiability of a function implies:
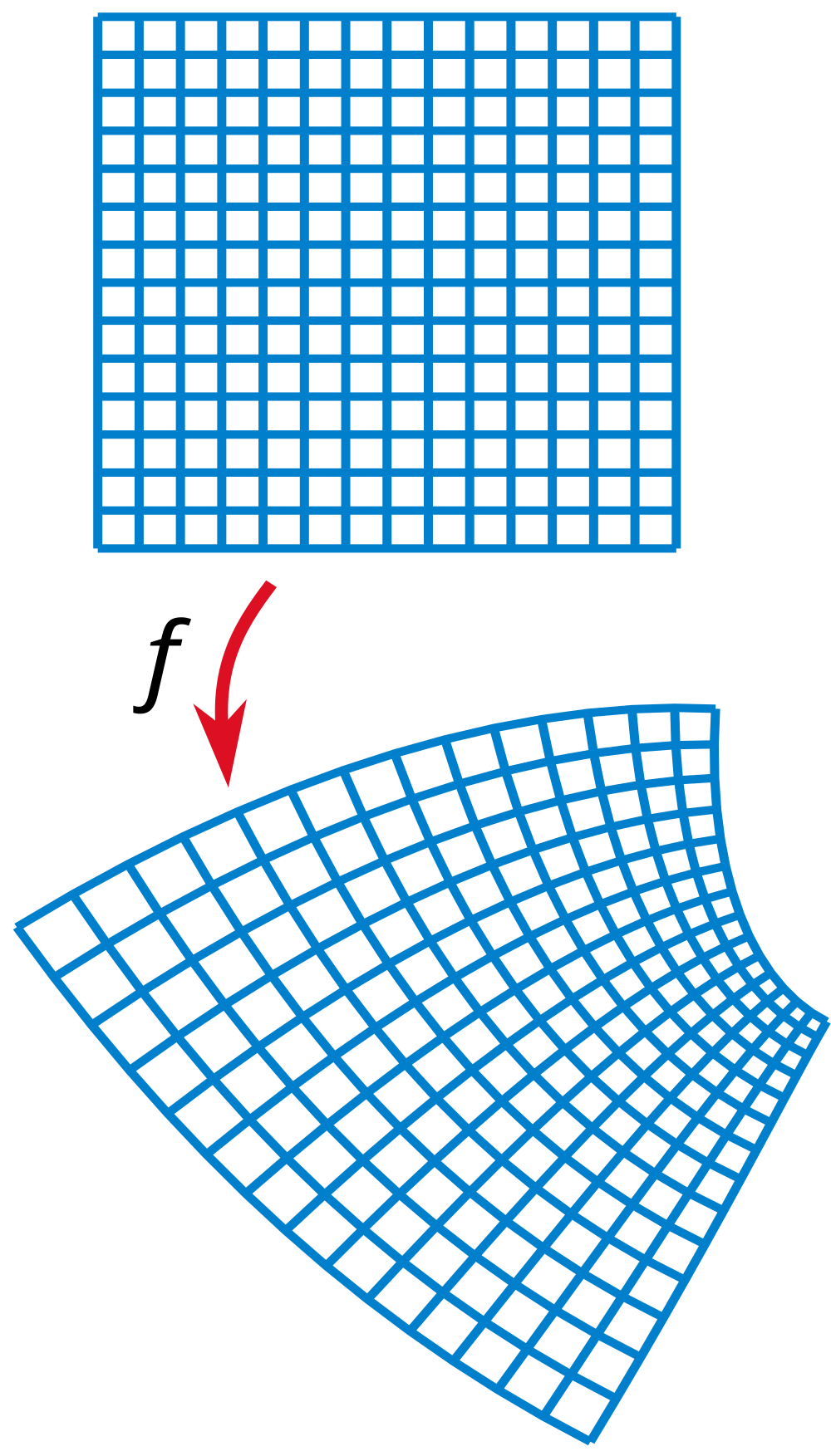
ℂ→ℂ mappings mess with my head…and I like it.
z² / z² + 2z + 2
on WolframAlpha. That’s Wikipedia’s example of a function with two poles (= two singularities = two infinities). Notice how “boring” line-only pictures are compared to the the 3-D ℂ→>ℝ picture of the mapping (the one with the poles=holes). That’s why mathematicians say ℂ uncovers more of “what’s really going on”.
As opposed to normal differentiability, ℂ-differentiability of a function implies:
- infinite descent into derivatives is possible (no chain of
C¹ ⊂ C² ⊂ C³ ... Cωlike usual)
nice Green’s-theorem type shortcuts make many, many ways of doing something equivalent. (So you can take a complicated real-world situation and validly do easy computations to understand it, because a squibbledy path computes the same as a straight path.)
Pretty interesting to just change things around and see how the parts work.
- The roots of the denominator are
1+iand1−i(of course the conjugate of a root is always a root sinceiand−iare indistinguishable) - you can see how the denominator twists
- a fraction in ℂ space maps lines to circles, because lines and circles are turned inside out (they are just flips of each other: see also projective geometry)
- if you change the
z^2/to az/or a1/you can see that. - then the Wikipedia picture shows the poles (infinities)
z are mod z • exp(i • arg z).- Apparently this is related to fluid mechanics and also QM somehow? And of course, tachyons!
- Angles. All it took was angles (angle-preserving maps = conformal maps = holomorphic = ℂ-differentiable). Compare: diffeomorphism.

ℂ→ℂ mappings mess with my head…and I like it.
No comments:
Post a Comment