物理量及微分運算有不變性(任何座標系普遍適用),
愛因斯坦方程式超簡介
距離的定義
距離,是 "兩點之間的長度",而此長度是一個實數。
距離的計算方法
直接量
由兩點分量差,利用畢氏定理
Δs2 = Δx2 + Δy2 + Δz2
( 或表示為 Δs2 = Δx12 + Δx22 + Δx32 )
可定義 距離函數 d(x, y) = [ (y1-x1)2 + (y2-x2)2 + (y3-x3)2 ](1/2) (畢氏定理)補充:
有了距離的觀念,可以分遠近。即區分那一些點在某個點的旁邊,那一些不是。能定義鄰近(neighborhood),就能定義開集合與拓撲,我們就有觀念上的工具可以描述東西大致們形體構造(如有洞的與沒有洞是不同的),即不一定有固定形體的。
宇宙正膨脹中的意涵:以前兩點之間距離較近,後來變遠了。
距離的定義的推廣
距離應有的性質單位向量與測度之間的關係
d(x, x) = 0:一個點到自己的距離為零
d(x, y) > 0:if x, y 不同點,大於零
d(x,z) < d(x,y) + d(y,z) :三角不等式(兩邊長之和大於第三邊)
滿足上述條件的定義
距離函數 d(x, y) = [ (y2-x2)2 + (y1-x1)2 ](1/2)
另一個距離函數 d'(x, y) = [ 4(y2-x2)2 + (y1-x1)2 ](1/2)
又另一個距離函數 d''(x, y) = max (| y2-x2|, | y1-x1| )
ds2 = Σij gij dxi dxj
這是在張量(幾何)的語言中,定義線段長度的方式
gij = ei · ej
其中
ei ≡ ∂/∂xi
張量與座標變化的不變性
向量、向量分量、算子與基底的形式
座標變換利用空間自已的自然參數作座標系統
需滿足什麼條件?
向量的分量值會改變
物理量不變
連(物理定律中常用的)向量微分的算子,也希望形式不變
要如何做到?
物理量由(向量或張量的)分量與基底向量所共同組成,刻意取成搭配的協變與反協變張量,例如 v = vi ei 或 A = Aij ei ej(在此已使用 summenstion convention,即成對出現的相同指標自動視為要作 Σ i=1. . . N 加總),如此一來不管參考座標系統如何更改,都自動保證所組合成的物理量 不隨座標變換而不同。
至於微分算子,則考慮不同位置點上如何"平移"一個向量的規則。從另一個角度說,是一個向量被微分時,除了分量被微分外,基底也有變化上的效應。
好處
物理量及微分運算有不變性(任何座標系普遍適用),才能讓以數學式表現的物理定律有不變性 (任何座標系普遍適用)
局部座標系協變張量與反協變張量
基底的選用
用切線作基底的必要性
自然的基底向量:切線向量
協變張量與反協變張量的互換:透過測度張量
協變微分
協同變?怎麼變?
Γij k 的特寫
從何而來?有何作用?Γij k 的重要性
函數的切線向量在彎曲空間 會有 "基底向量的改變" 之效應
函數的切線向量在平坦空間 不會有 基底向量的改變 之效應
切線向量嵌入在高維度空間才能看出有沒有改變方向
補充:曲面上,兩點間最短線的曲線又叫測地線 (geodesic line)。法方向上投影呈直線,符合兩點之間最短距離的線是直線。
剩下的觀念問題是,如何提取出(線、面、體的) "曲率" 而確定空間彎曲的程度。這在微分幾何學與黎曼幾何學中會有系統化的建立。
回憶前面幾何單元,曲率越大,單位弧長變動的切線改變越大。
Γij k 的定義
基底向量隨著座標參數之變化而變化的情形:
[∂/∂xj ] ei = Γki j ek根據 Γij k 的定義,
Aij; k = [∂/∂xk + Γij k ] Aij
上式的詮釋:(第一項)函數本身隨參數變化、加上(第二項)因基底引起的變化。
有了它,才可定義符合張量之變換行為的微分,叫協變微分。如上,能把微分的作用 "V;k"寫成為指標的一部分,意味者微分過後之結果也是一個張量。
實例:梯度、散度、旋度算子
四維時空(狹義相對論的加入)
勞倫滋轉換
羅馬字指標與希臘字指標
曲率
曲線 -> 曲面 -> 彎曲空間, 都可以定 "曲率" (切線方向的變化率,因此要用到微分)
(數學的威力:模式.推廣)(愛因斯坦需要的,黎曼已經準備好)
待補:二維曲面上的曲率如何建立、三維曲面的曲率如何建立。
測度張量的彎曲,就是空間的彎曲
彎曲的程度,Richi
Geometrically, the Ricci curvature is the mathematical object that controls the growth rate of the volume of metric balls in a manifold.
若以測地線做為參數,則測度張量會有簡單的近似下形式.測度張量以泰勒展開至第一項得
gij = δij + O(|x|2)
以泰勒展開至第二項,則出現 Ricci 曲率張量 :
gij = δij + (1/3) Rijkl xkxl + O(|x|3)
(座標系)運動造成之加速度與重力造成之加速度的等效性
核心觀念:
重力造成的加速度與運動造成的加速度,其本質上(觀察上)不可區分,如果是這樣的話,重力的效果對應到怎麼樣的運動?
重力的新圖像:慣性直線運動(本來無一物,何處惹塵埃)
重力造成的加速度不是外力推動有質量的物體,而是空間彎曲,運動軌跡是則是該空間慣性運動所該有的直線運動。
新想法的結果:
就算是沒有質量的光子,也能被質量體改變路徑。這就超越了牛頓的超距性的萬有引力,並且留下了實驗可以驗證的機會。
曲率張量待選
愛因斯坦選出來的曲率張量
情況之一:空間彎曲只在物質存在(佔有空間之處),而非包含附近(排除)
情況之另一:
時空方程式
Rmn = (4πG/c4) ( 2Tmn - Tδmn )
Gμν = k Tμν
其中 Gμν = Rμν - 1/2gμν RGμν - Λ gμν= k Tμν( Λ 宇宙常數: 愛因斯坦自稱其一生中最大的錯誤)
這裏頭含有測度張量 g μν 的微分及組合,其總的數學意義是曲率。
愛因斯坦說,等號左旁是光滑、精緻、堅固、美麗的大理石(幾何)、右邊是粗糙、脆弱、拼湊的木頭(質量、能量、動量、應力),他自己喜歡左邊的部分。
(發現宇宙的膨脹是加速中之後,有人問:難到愛因斯坦終究還是對了嗎?)
不同數學條件下的空間幾何結構
向量空間
空間點可賦予向量於其上,可對存純量、向量、張量進行座標轉換
仿射空間
引入 Γijk ,可定基底向量跨不同空間點之變化律,可作協變微分。(在此已可得廣義的斜率)
測度空間
引入測度 gμν,可定向量長度
黎曼空間
要求 "向量" 在空間中被 "平行移動" 時,其長度不變
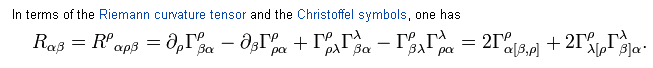
No comments:
Post a Comment