幂级数
维基百科,自由的百科全书
在数学中,幂级数是一类形式简单而应用广泛的函数级数,变量可以是一个或多个(见“多元幂级数”一节)。单变量的幂级数形式为:
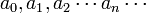 是常数。
是常数。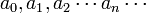 称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
如果把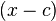 看成一项,那么幂级数可以化简为
看成一项,那么幂级数可以化简为 的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
将一个函数写成幂级数 的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
幂级数是分析学研究的重点之一,然而在组合数学中,幂级数也占有一席之地。作为母函数,由幂级数概念发展出来的形式幂级数是许多组合恒等式的来源[1]。在电力工程学中,幂级数则被称为Z-变换。实数的小数记法也可以被看做幂级数的一种,只不过这里的x被固定为 。在p-进数中则可以见到x被固定为
。在p-进数中则可以见到x被固定为 的幂级数。
的幂级数。
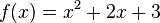 可以写成标准形式的幂级数:
可以写成标准形式的幂级数:
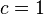 ):
):
等比级数的公式给出了对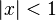 ,有
,有
幂级数里不包括负的幂次。例如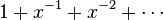 就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数
就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数 必须是和x无关,比如
必须是和x无关,比如 就不是一个幂级数。
就不是一个幂级数。
按照引理,使得幂级数 收敛的复数的集合总是某个以原点为中心的圆(不包括边界),称为收敛圆盘,其边界称为收敛圆。具体来说,就是:
收敛的复数的集合总是某个以原点为中心的圆(不包括边界),称为收敛圆盘,其边界称为收敛圆。具体来说,就是:
 被称为幂级数的收敛半径,当属于第一种情况时,规定收敛半径为零。
被称为幂级数的收敛半径,当属于第一种情况时,规定收敛半径为零。
按照定义,对一个幂级数 ,当
,当 (在收敛圆盘内)时(如果有的话),幂级数必然收敛;而当
(在收敛圆盘内)时(如果有的话),幂级数必然收敛;而当 时(如果有的话),幂级数必然发散。但是如果
时(如果有的话),幂级数必然发散。但是如果 (在收敛圆上)的话,这时幂级数的敛散性是无从判断的,只能具体分析。
(在收敛圆上)的话,这时幂级数的敛散性是无从判断的,只能具体分析。
根据达朗贝尔审敛法,收敛半径 满足:如果幂级数
满足:如果幂级数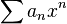 满足
满足 ,则:
,则:
 ,可以证明,幂级数在收敛圆盘上一致收敛。这个性质称为内闭一致收敛。因此,考虑幂级数函数
,可以证明,幂级数在收敛圆盘上一致收敛。这个性质称为内闭一致收敛。因此,考虑幂级数函数
 的收敛半径R。具体形式为:
的收敛半径R。具体形式为:
 为确定的常数。
为确定的常数。
如果一个函数在某处可展,那么它在这点无穷可导( ),并且在这点附近的展开式是唯一的。
),并且在这点附近的展开式是唯一的。
 ,也可以写出幂级数
,也可以写出幂级数 ,但即使这个幂级数收敛,其值也不一定等于
,但即使这个幂级数收敛,其值也不一定等于  。例如函数
。例如函数 :
:
 无穷可导,并且在0处的每阶导数都是零,因此相应的幂级数
无穷可导,并且在0处的每阶导数都是零,因此相应的幂级数 恒等于0,不等于
恒等于0,不等于  。
。
函数可以展开成幂级数的充要条件是其泰勒展开的余项趋于零: ,
,
一个更常用到的充分条件是: 如果存在正实数r,使得 在区间
在区间 上无穷可导,并且存在正数M使得对任意的 n,任意的
上无穷可导,并且存在正数M使得对任意的 n,任意的 都有
都有
 可以在c附近展开成幂级数:
可以在c附近展开成幂级数:
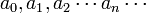 是常数。
是常数。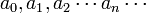 称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。
称为幂级数的系数。幂级数中的每一项都是一个幂函数,幂次为非负整数。幂级数的形式很像多项式,在很多方面有类似的性质,可以被看成是“无穷次的多项式”。如果把
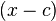 看成一项,那么幂级数可以化简为
看成一项,那么幂级数可以化简为 的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。
的形式。后者被称为幂级数的标准形式。一个标准形式的幂级数完全由它的系数来决定。将一个函数写成幂级数
 的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。
的形式称为将函数在c处展开成幂级数。不是每个函数都可以展开成幂级数。幂级数是分析学研究的重点之一,然而在组合数学中,幂级数也占有一席之地。作为母函数,由幂级数概念发展出来的形式幂级数是许多组合恒等式的来源[1]。在电力工程学中,幂级数则被称为Z-变换。实数的小数记法也可以被看做幂级数的一种,只不过这里的x被固定为
 。在p-进数中则可以见到x被固定为
。在p-进数中则可以见到x被固定为 的幂级数。
的幂级数。目录[隐藏] |
[编辑] 例子
多项式可以看做系数从某一项开始全是零的幂级数,例如多项式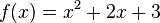 可以写成标准形式的幂级数:
可以写成标准形式的幂级数: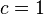 ):
):等比级数的公式给出了对
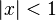 ,有
,有-
 ,
,
幂级数里不包括负的幂次。例如
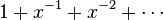 就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数
就不是幂级数(它是一个劳伦级数)。同样的,幂次为分数的级数也不是幂级数。系数 必须是和x无关,比如
必须是和x无关,比如 就不是一个幂级数。
就不是一个幂级数。[编辑] 敛散性
作为级数的一种,幂级数的敛散性也是研究幂级数的重点之一。对同一个幂级数,当变量x在复数中变化时,幂级数可能收敛,也可能发散。作为判断的依据,有:- 阿贝尔引理:给定一个幂级数
 ,如果对实数
,如果对实数 ,数列
,数列 有界,那么对任意复数
有界,那么对任意复数 ,
, 绝对收敛。
绝对收敛。
显示▼证明
 收敛的复数的集合总是某个以原点为中心的圆(不包括边界),称为收敛圆盘,其边界称为收敛圆。具体来说,就是:
收敛的复数的集合总是某个以原点为中心的圆(不包括边界),称为收敛圆盘,其边界称为收敛圆。具体来说,就是:- 要么对所有的非零复数,
 都发散;
都发散; - 要么存在一个正常数(包括正无穷)
 ,使得当
,使得当 时,
时, 绝对收敛,当
绝对收敛,当 时,
时, 发散。
发散。
 被称为幂级数的收敛半径,当属于第一种情况时,规定收敛半径为零。
被称为幂级数的收敛半径,当属于第一种情况时,规定收敛半径为零。按照定义,对一个幂级数
 ,当
,当 (在收敛圆盘内)时(如果有的话),幂级数必然收敛;而当
(在收敛圆盘内)时(如果有的话),幂级数必然收敛;而当 时(如果有的话),幂级数必然发散。但是如果
时(如果有的话),幂级数必然发散。但是如果 (在收敛圆上)的话,这时幂级数的敛散性是无从判断的,只能具体分析。
(在收敛圆上)的话,这时幂级数的敛散性是无从判断的,只能具体分析。根据达朗贝尔审敛法,收敛半径
 满足:如果幂级数
满足:如果幂级数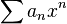 满足
满足 ,则:
,则: 是正实数时,
是正实数时, 。
。 时,
时, 。
。 时,
时, 。
。

- 或者
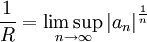 。
。
[编辑] 幂级数的运算
形式上,幂级数的加减法运算是将相应系数进行加减。

 。
。
[编辑] 一致收敛性
对一个收敛半径为R的幂级数 ,可以证明,幂级数在收敛圆盘上一致收敛。这个性质称为内闭一致收敛。因此,考虑幂级数函数
,可以证明,幂级数在收敛圆盘上一致收敛。这个性质称为内闭一致收敛。因此,考虑幂级数函数[编辑] 幂级数函数的求导和积分
可以证明,幂级数函数f在收敛区间上无穷次可导,并且可积。此外,由于幂级数函数f在收敛圆盘内一致收敛,可以进行逐项求导和积分,而且其导函数和积分函数都是在收敛区间上连续的幂级数函数。它们的收敛半径等于 的收敛半径R。具体形式为:
的收敛半径R。具体形式为:[编辑] 函数的幂级数展开
鉴于幂级数函数的良好分析性质以及对之深入的研究,如能将要研究的函数以幂级数形式来表示,将有助于对其性质的研究。然而,不是所有的函数都能展开为幂级数。一个函数在一点 c 附近可展(可以展开为幂级数),当且仅当存在正实数 R>0,使得在复平面中以 c 为圆心以 R 为半径的圆D(c,R) 内(不包括边界)有: 为确定的常数。
为确定的常数。如果一个函数在某处可展,那么它在这点无穷可导(
 ),并且在这点附近的展开式是唯一的。
),并且在这点附近的展开式是唯一的。[编辑] 函数的可展性
对于一般的无穷可导函数 ,也可以写出幂级数
,也可以写出幂级数 ,但即使这个幂级数收敛,其值也不一定等于
,但即使这个幂级数收敛,其值也不一定等于  。例如函数
。例如函数 :
:- 当 x>0时,

- 当
 时,
时, 
 无穷可导,并且在0处的每阶导数都是零,因此相应的幂级数
无穷可导,并且在0处的每阶导数都是零,因此相应的幂级数 恒等于0,不等于
恒等于0,不等于  。
。函数可以展开成幂级数的充要条件是其泰勒展开的余项趋于零:
 ,
,一个更常用到的充分条件是: 如果存在正实数r,使得
 在区间
在区间 上无穷可导,并且存在正数M使得对任意的 n,任意的
上无穷可导,并且存在正数M使得对任意的 n,任意的 都有
都有 ,
,
 可以在c附近展开成幂级数:
可以在c附近展开成幂级数: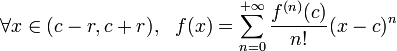 。
。
[编辑] 常见函数的幂级数展开
以下是一些常见函数的幂级数展开。运用这些展开可以得到一些重要的恒等式。


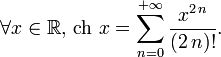

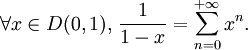
![\forall x\in(-1,1],\, \ln (1+x)=\sum_{n=1}^{+{\infty}}(-1)^{n+1}{x^{n}\over{n}}.](http://upload.wikimedia.org/math/2/9/a/29a224830e09ccd9df0592528ef1cb9d.png)
![\forall x\in[-1,1],\, \arctan \,x=\sum_{n=0}^{+{\infty}}(-1)^n\,{\frac{x^{2\,n+1}}{2\,n+1}}\;](http://upload.wikimedia.org/math/f/5/f/f5f63baa6d224122a022dbc96dd49fa8.png) ,特别地,
,特别地, 。
。

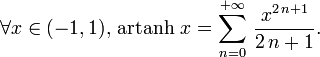

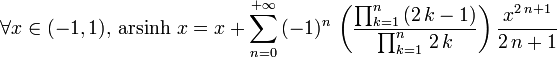
 ,其中
,其中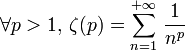



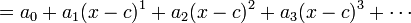


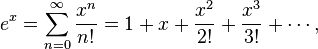

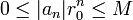 。所以:
。所以: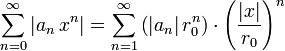
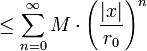

 严格小于1,因此上面的
严格小于1,因此上面的


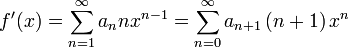

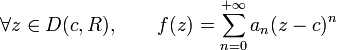


No comments:
Post a Comment