 的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離
的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離  ,可以使得O點成為拐點,則可以保證
,可以使得O點成為拐點,則可以保證  級項目為零,因此領先不均勻項目是
級項目為零,因此領先不均勻項目是  級項目。
級項目。亥姆霍茲線圈
维基百科,自由的百科全书
亥姆霍茲線圈(Helmholtz coil)是一種製造小範圍區域均勻磁場的器件。由於亥姆霍茲線圈具有開敞性質,很容易地可以將其它儀器置入或移出,也可以直接做視覺觀察,所以,是物理實驗常使用的器件。因德國物理學者赫爾曼·馮·亥姆霍茲而命名。
 的圓形線圈的中心軸都與z-軸同軸。兩個圓形線圈的z-坐標分別為
的圓形線圈的中心軸都與z-軸同軸。兩個圓形線圈的z-坐標分別為  與
與  。每一個導體線圈載有同向電流
。每一個導體線圈載有同向電流  。
。
設定 可以使得在兩個線圈中心位置O(即原點)的磁場,其不均勻程度極小化。這動作促使
可以使得在兩個線圈中心位置O(即原點)的磁場,其不均勻程度極小化。這動作促使  ,也意味著領先的非零微分項目是
,也意味著領先的非零微分項目是  ,稍後會對這論點做更詳細解釋。[1] 但是,這樣做仍舊會在線圈平面跟z-軸相交處與O點之間遺留大約 7% 磁場數值的差別。
,稍後會對這論點做更詳細解釋。[1] 但是,這樣做仍舊會在線圈平面跟z-軸相交處與O點之間遺留大約 7% 磁場數值的差別。
在某些应用中,亥姆霍茲線圈可以用來抵消地磁場,製造出接近零磁場的區域。[2]
 的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離
的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離  ,可以使得O點成為拐點,則可以保證
,可以使得O點成為拐點,則可以保證  級項目為零,因此領先不均勻項目是
級項目為零,因此領先不均勻項目是  級項目。
級項目。
在中心位置O點,磁場為
 是磁常數。
是磁常數。
 是磁場數值大小,
是磁場數值大小, 是磁常數,
是磁常數, 是電流,
是電流, 是線圈半徑,
是線圈半徑, 是檢驗位置的z-坐標。
是檢驗位置的z-坐標。
對於 匝線圈,磁場為
匝線圈,磁場為
 ,注意到每一個亥姆霍茲線圈有一對線圈,所以,總磁場為
,注意到每一個亥姆霍茲線圈有一對線圈,所以,總磁場為
 的冪級數:
的冪級數:
 。
。
現在設定 ,則
,則  項目為零,在原點附近的磁場更加均勻:
項目為零,在原點附近的磁場更加均勻:
 的關係式為
的關係式為
 ,線圈平面與z-軸相交處,磁場數值的差別為
,線圈平面與z-軸相交處,磁場數值的差別為
目录[隐藏] |
[编辑] 簡介
亥姆霍茲線圈是由一對完全相同的圓形導體線圈組成。採用直角坐標系,這兩個半徑為 的圓形線圈的中心軸都與z-軸同軸。兩個圓形線圈的z-坐標分別為
的圓形線圈的中心軸都與z-軸同軸。兩個圓形線圈的z-坐標分別為  與
與  。每一個導體線圈載有同向電流
。每一個導體線圈載有同向電流  。
。設定
 可以使得在兩個線圈中心位置O(即原點)的磁場,其不均勻程度極小化。這動作促使
可以使得在兩個線圈中心位置O(即原點)的磁場,其不均勻程度極小化。這動作促使  ,也意味著領先的非零微分項目是
,也意味著領先的非零微分項目是  ,稍後會對這論點做更詳細解釋。[1] 但是,這樣做仍舊會在線圈平面跟z-軸相交處與O點之間遺留大約 7% 磁場數值的差別。
,稍後會對這論點做更詳細解釋。[1] 但是,這樣做仍舊會在線圈平面跟z-軸相交處與O點之間遺留大約 7% 磁場數值的差別。在某些应用中,亥姆霍茲線圈可以用來抵消地磁場,製造出接近零磁場的區域。[2]
[编辑] 數學描述
關於在空間任意位置的精確磁場計算,需要應用到貝索函數或橢圓函數與其相關技巧。沿著線圈的中心軸(z-軸),涉及到的計算比較簡單,可以應用泰勒展開,將磁場展開為 的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離
的冪級數。採用直角坐標系,以亥姆霍茲線圈的中心位置為z-軸的原點O。由於對於xy-平面的對稱性,奇數冪項目必等於零。經過調整兩個線圈之間的距離  ,可以使得O點成為拐點,則可以保證
,可以使得O點成為拐點,則可以保證  級項目為零,因此領先不均勻項目是
級項目為零,因此領先不均勻項目是  級項目。
級項目。在中心位置O點,磁場為
 ;
;
 是磁常數。
是磁常數。[编辑] 推導
採用直角坐標系,設定單匝線圈的中心軸為z-軸,線圈平面與z-軸相交處為原點,則在z-軸的磁場以方程式表示為[3](這方程式可以從必歐-沙伐定律推導出來) ;
;
 是磁場數值大小,
是磁場數值大小, 是磁常數,
是磁常數, 是電流,
是電流, 是線圈半徑,
是線圈半徑, 是檢驗位置的z-坐標。
是檢驗位置的z-坐標。對於
 匝線圈,磁場為
匝線圈,磁場為 。
。
 ,注意到每一個亥姆霍茲線圈有一對線圈,所以,總磁場為
,注意到每一個亥姆霍茲線圈有一對線圈,所以,總磁場為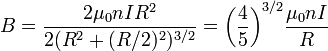 。
。
[编辑] 進階推導
更詳細地計算,沿著z-軸的磁場為兩個線圈的貢獻的疊加:[4]![\mathbf{B} =\frac{\mu_0 I R^2}{2} \left\{\left[R^2+(z-h/2)^2\right]^{-3/2}
+\left[R^2+(z+h/2)^2\right]^{-3/2}\right\}\hat{\mathbf{z}}](http://upload.wikimedia.org/math/6/3/8/638b64cd78e10d85aaa8edba108ce6d2.png) 。
。
 的冪級數:
的冪級數:![\mathbf{B} =\frac{\mu_0 I R^2}{d^3}\left[1+\frac{3(h^2-R^2)z^2}{2d^4}+\frac{15(h^4-6h^2R^2+2R^4)z^4}{16d^8}+\dots\right]\hat{\mathbf{z}}](http://upload.wikimedia.org/math/1/9/a/19a599f1f1c8bf9c0b9800f167a3a031.png) ;
;
 。
。現在設定
 ,則
,則  項目為零,在原點附近的磁場更加均勻:
項目為零,在原點附近的磁場更加均勻:![\mathbf{B} ={\left ( \frac{4}{5} \right )}^{3/2} \frac{\mu_0 I}{R}\left[1-\frac{144}{125}\ \left(\frac{z}{R}\right)^4+\dots\right]\hat{\mathbf{z}}](http://upload.wikimedia.org/math/a/6/7/a674ea67755efc51c9f0ad50b0e22405.png) 。
。
 的關係式為
的關係式為 。
。
 ,線圈平面與z-軸相交處,磁場數值的差別為
,線圈平面與z-軸相交處,磁場數值的差別為




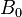 相差不超過1%。五條等值線的磁場數值分別為
相差不超過1%。五條等值線的磁場數值分別為  、
、 、
、 、
、 、
、 。
。
No comments:
Post a Comment