http://www.ck365.cn/lunwen/201207/25/19055.html
光强公式和测量公式均是从(1)式导出的,而基尔霍夫在导出(1)式时,是将光波当作标量波处理的,其核心思想是用边界上的复振幅分布来表达观察点的复振幅。如果边界上的复振幅分布相同,即使光振动的方向不同,观察点的复振幅也应该相同。严格说来,应该把光场看成矢量场,并考虑光场与衍射物质的相互作用。因此只有在满足:(1)r>>入;(2)衍射孔径>>入两个条件的情况下,标量理论才是准确的。显然,条件(1)是容易满足的,间题是对于条件(2),当衍射孔小到什么程度时标量理论不再适用。通常很难给出一个准确的下限。幸运的是,当衍射孔小到接近波长的时候,此理论还能与实际观测相当好地符合。
用夫朗和费衍射测量微小物体的尺寸
发布时间:2012-07-25来源:互联网
我要说几句 |


厉江帆
葛万福 张佃中
(长沙电力学院咬10077) (佛山太阳包装有限公司52800) (湖南医科大学)
提要:文[1〕的结论是错误的.微小物体最小可测尺寸仅由标量理论的成立范围决定,在标量理论允许的范围内,只要正确地应用实验装置和测量公式,便能得到准确的测量结果,测量的正确度与物体的尺寸和衍射角的大小无关。
关键词 衍射 夫朗和费近似 测量 正确度
在光学测量中,常用夫朗和费衍射测量微小物体的尺寸。文〔1」以单狭缝为例,讨论了用夫朗和费衍射测量微小尺寸的正确度问题。认为要获得正确的测量结果,除需要满足夫朗和费近似外,还必须对衍射角有一定的限制。所测的衍射角越大,测量的正确度越低。由于衍射角和微小物体的大小直接相关,物体尺寸越小,衍射愈甚,系统误差越大。本文认为这一结论是错误的。导致错误的原因是将一个仅在小衍射角情形下成立的近似公式,当成衍射测量必须使用的公式。本文指出测量的最小宽度仅由标量理论的适用范围所限制,在标量理论成立的范围内,只要正确地使用实验装置和测量公式,便能得到准确的结果。测量的正确度与狭缝宽度和衍射角的大小无关。
夫朗和费衍射的实验装置
图1为夫朗和费衍射的定义装置。该装置在概念上是简明的,能直观地将夫朗和费衍射和菲徨耳衍射区分开来。其意义是强调衍射场的角分布,把复杂的衍射场分解为一系列的平面波。但在实验上是抽象的。在实际中,为了缩短装置的空间长度,常用图2的焦面接收装置,得到准确的夫朗和费衍射花样,缺点是对透镜的要求较高。为简单起见,常采用图3的远扬接收装置。当衍射孔很小,Z很大时,屏上的衍射花样非常接近于夫朗和费衍射花样。激光的出现,使这一装置的实用成为可能。

 图2焦面接收装置
图2焦面接收装置
 图3远扬接收装置
图3远扬接收装置
光强公式和测量公式
不管衍射屏或被测物的形状如何,其测量原理是一样的。下面我们也以单狭缝为例进行讨论。标量理论的衍射公式为


这里I。为焦面上衍射化样中心点的光强。这种情形,在标量理论的基尔霍夫公式中,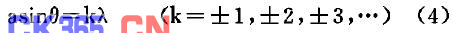
 范围内,有
范围内,有 。显然,
。显然, 为随
为随 单调缓慢减少的函数,且有
单调缓慢减少的函数,且有 从而,当
从而,当
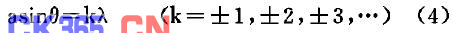 时,有
时,有 即出现第k级衍射最小。在实际测量中,通常测出两k级暗纹之间的距离
即出现第k级衍射最小。在实际测量中,通常测出两k级暗纹之间的距离 再将
再将 代入(4)得测量公式
代入(4)得测量公式
 在图3的远场装置中,当Z大到从衍射孔发出的到达考察点q的所有光线都可看成近似平行时,屏上花样即为近似的夫朗和费衍射花样。其强度分布由(3)式描述,衍射极小的位置由(4)式决定。由图3可知,此时,与(5)式相对应的测量公式为
在图3的远场装置中,当Z大到从衍射孔发出的到达考察点q的所有光线都可看成近似平行时,屏上花样即为近似的夫朗和费衍射花样。其强度分布由(3)式描述,衍射极小的位置由(4)式决定。由图3可知,此时,与(5)式相对应的测量公式为

结论
(1)孙贵林,光学技术,1995,2,36
(2)幻黄婉云编,《傅里叶光学教程》,北京师范大学出版社,第一版,1985,100
(3)M.C.哈特雷著,贾惟仪等译,《衍射光栅》,贵州人民出版社,第一版,1990,199
(长沙电力学院咬10077) (佛山太阳包装有限公司52800) (湖南医科大学)
提要:文[1〕的结论是错误的.微小物体最小可测尺寸仅由标量理论的成立范围决定,在标量理论允许的范围内,只要正确地应用实验装置和测量公式,便能得到准确的测量结果,测量的正确度与物体的尺寸和衍射角的大小无关。
关键词 衍射 夫朗和费近似 测量 正确度
在光学测量中,常用夫朗和费衍射测量微小物体的尺寸。文〔1」以单狭缝为例,讨论了用夫朗和费衍射测量微小尺寸的正确度问题。认为要获得正确的测量结果,除需要满足夫朗和费近似外,还必须对衍射角有一定的限制。所测的衍射角越大,测量的正确度越低。由于衍射角和微小物体的大小直接相关,物体尺寸越小,衍射愈甚,系统误差越大。本文认为这一结论是错误的。导致错误的原因是将一个仅在小衍射角情形下成立的近似公式,当成衍射测量必须使用的公式。本文指出测量的最小宽度仅由标量理论的适用范围所限制,在标量理论成立的范围内,只要正确地使用实验装置和测量公式,便能得到准确的结果。测量的正确度与狭缝宽度和衍射角的大小无关。
夫朗和费衍射的实验装置
图1为夫朗和费衍射的定义装置。该装置在概念上是简明的,能直观地将夫朗和费衍射和菲徨耳衍射区分开来。其意义是强调衍射场的角分布,把复杂的衍射场分解为一系列的平面波。但在实验上是抽象的。在实际中,为了缩短装置的空间长度,常用图2的焦面接收装置,得到准确的夫朗和费衍射花样,缺点是对透镜的要求较高。为简单起见,常采用图3的远扬接收装置。当衍射孔很小,Z很大时,屏上的衍射花样非常接近于夫朗和费衍射花样。激光的出现,使这一装置的实用成为可能。



光强公式和测量公式
不管衍射屏或被测物的形状如何,其测量原理是一样的。下面我们也以单狭缝为例进行讨论。标量理论的衍射公式为

这里u(p)为衍射孔 上任意一点p的复振幅,
上任意一点p的复振幅, 为倾斜因子,r为p点到达观察点q的光程。
为倾斜因子,r为p点到达观察点q的光程。
在图2的焦面接收装置中,设缝宽为a,缝中点到达焦面上q点的光程为r。,则有 。通常有
。通常有 ,故可将(1)在很高的精度上简化为
,故可将(1)在很高的精度上简化为

从而得q点的光强为

这里I。为焦面上衍射化样中心点的光强。这种情形,在标量理论的基尔霍夫公式中,
显然,当衍射角较小时,(6)式退化为文「1〕的(14)式,该式仅当所测角度不大时可以使用;当衍射角十分微小,即 时,(6)式自然简化为文[l〕的(9)式。
时,(6)式自然简化为文[l〕的(9)式。

文[2〕指出,当
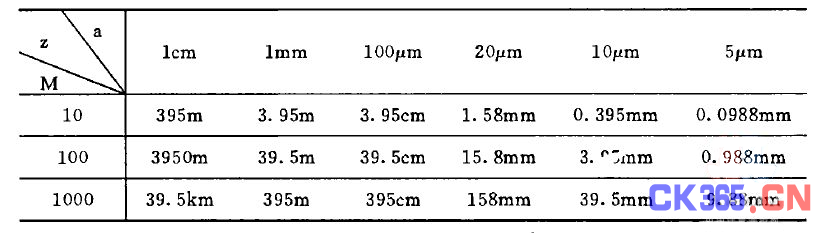
 ,(通常取M=10,精度要求较高时,亦取M=100)时,在接收屏上所观察到的衍射可看成近似的夫朗和费衍射。下面列出入=0.6528
,(通常取M=10,精度要求较高时,亦取M=100)时,在接收屏上所观察到的衍射可看成近似的夫朗和费衍射。下面列出入=0.6528 ,M取10,100,甚至大到1000,a取不同的值时,Z的取值情况。以期对夫朗和费近似条件有一较直观的理解。由上表可看出,当缝宽在厘米数量级或更大时,采用图(3)的远扬装置是欠妥当的。但利用焦面接收装置却能十分容易地得到准确的夫朗和费衍射。当a在1毫米左右时,位于5米左右的观察屏能接收到近似的夫朗和费衍射花样。当a进一步地减小,如在10微米左右时,观察屏放在很近的距离,仍能得到非常准确的夫朗和费衍射花样。
,M取10,100,甚至大到1000,a取不同的值时,Z的取值情况。以期对夫朗和费近似条件有一较直观的理解。由上表可看出,当缝宽在厘米数量级或更大时,采用图(3)的远扬装置是欠妥当的。但利用焦面接收装置却能十分容易地得到准确的夫朗和费衍射。当a在1毫米左右时,位于5米左右的观察屏能接收到近似的夫朗和费衍射花样。当a进一步地减小,如在10微米左右时,观察屏放在很近的距离,仍能得到非常准确的夫朗和费衍射花样。
最小可测宽度上述光强公式和测量公式均是从(1)式导出的,而基尔霍夫在导出(1)式时,是将光波当作标量波处理的,其核心思想是用边界上的复振幅分布来表达观察点的复振幅。如果边界上的复振幅分布相同,即使光振动的方向不同,观察点的复振幅也应该相同。严格说来,应该把光场看成矢量场,并考虑光场与衍射物质的相互作用。因此只有在满足:(1)r>>入;(2)衍射孔径>>入两个条件的情况下,标量理论才是准确的。显然,条件(1)是容易满足的,间题是对于条件(2),当衍射孔小到什么程度时标量理论不再适用。通常很难给出一个准确的下限。幸运的是,当衍射孔小到接近波长的时候,此理论还能与实际观测相当好地符合。以高分辨率的刻划光栅为例,当光栅常数十分微小时,由此理论导出的光栅方程还惊人地正确。在刻槽不太深,入射角不太大的情形下,光栅槽距等于5倍波长时,其效率反常和偏振效应还不十分严重。标量理论可以使用(3)。结论
最小可测宽度上述光强公式和测量公式均是从(1)式导出的,而基尔霍夫在导出(1)式时,是将光波当作标量波处理的,其核心思想是用边界上的复振幅分布来表达观察点的复振幅。如果边界上的复振幅分布相同,即使光振动的方向不同,观察点的复振幅也应该相同。严格说来,应该把光场看成矢量场,并考虑光场与衍射物质的相互作用。因此只有在满足:(1)r>>入;(2)衍射孔径>>入两个条件的情况下,标量理论才是准确的。显然,条件(1)是容易满足的,间题是对于条件(2),当衍射孔小到什么程度时标量理论不再适用。通常很难给出一个准确的下限。幸运的是,当衍射孔小到接近波长的时候,此理论还能与实际观测相当好地符合。以高分辨率的刻划光栅为例,当光栅常数十分微小时,由此理论导出的光栅方程还惊人地正确。在刻槽不太深,入射角不太大的情形下,光栅槽距等于5倍波长时,其效率反常和偏振效应还不十分严重。标量由以上分析可知,一般情形下,可选用焦面接收装置,准确地实现夫朗和费衍射。但当测量微小尺寸时,亦可选用较简单的远场接收装置近似地实现夫朗和费衍射。衍射孔越小,必有衍射角越大,同时也越容易在较近的距离接收到足够准确的夫朗和费衍射花样。此时必须应用公式(6)进行计算,才能得到与实际尺寸相吻合的结果。因此,文〔1〕将仅在小衍射角情形下成立的近似公式(9)当作衍射测量的通用公式,并将因使用(9)于较大角度情形而导致的偏差视为衍射法本身的系统误差是欠妥当的。另外,文〔1〕有关光栅常数的测量一例,由光栅方程 得到三次测量的光栅常数分别为
得到三次测量的光栅常数分别为 (计算时可将测量数据直接代入本文等式(6)右边而得d)。数据的微小差别是由测量的偶然误差引起的。这三次测量对应的衍射角分别为3.62。,7.28。,10.94。(文〔1〕计算有误)。并不能得出所测的衍射角越大,测量精度越低的结论。最后,还必须指出的是文[l]的表2也仅能说明,当缝宽十分微小(但在标量理论可以应用的线度内),以致可测量的最小衍射角(k一1)亦很大时,不能用(9)式甚至(14)式进行计算。但并不意味着不能用衍射法对此宽度进行准确的测量,只要测量后用(6)式进行计算便能得到正确的结果。
(计算时可将测量数据直接代入本文等式(6)右边而得d)。数据的微小差别是由测量的偶然误差引起的。这三次测量对应的衍射角分别为3.62。,7.28。,10.94。(文〔1〕计算有误)。并不能得出所测的衍射角越大,测量精度越低的结论。最后,还必须指出的是文[l]的表2也仅能说明,当缝宽十分微小(但在标量理论可以应用的线度内),以致可测量的最小衍射角(k一1)亦很大时,不能用(9)式甚至(14)式进行计算。但并不意味着不能用衍射法对此宽度进行准确的测量,只要测量后用(6)式进行计算便能得到正确的结果。
参考文献(1)孙贵林,光学技术,1995,2,36
(2)幻黄婉云编,《傅里叶光学教程》,北京师范大学出版社,第一版,1985,100
(3)M.C.哈特雷著,贾惟仪等译,《衍射光栅》,贵州人民出版社,第一版,1990,199

No comments:
Post a Comment