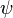Friday, April 19, 2013

qm01 對於任何位勢，都有一個明顯的簡併(•Conjugate)：假若波函數 \psi\,\! 是某薛定諤方程式的解答，則其共軛函數 \psi^*\,\! 也是這薛定諤方程式的解答

對於任何位勢，都有一個明顯的簡併：假若波函數 $\psi\,\!$ 是某薛定諤方程式的解答，則其共軛函數 $\psi^*\,\!$ 也是這薛定諤方程式的解答

http://zh.wikipedia.org/wiki/%E8%96%9B%E5%AE%9A%E8%B0%94%E6%96%B9%E7%A8%8B

實值的本徵態
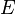不含時薛定諤方程式的波函數解答，也符合線性關係。但在這狀況，線性關係有稍微不同的意義。假若兩個波函數 $\psi_A\,\!$ 與 $\psi_B\,\!$ 都是某不含時薛定諤方程式的，能量為 $E\,\!$ 的解答，則這兩個不同的波函數解答為簡併的。任何線性組合也是能量為 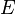$E\,\!$ 的解答。

$- \frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}(a\psi_A+b\psi_B)+V(a\psi_A+b\psi_B)=E(a\psi_A+b\psi_B)\,\!$ 。

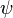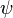對於任何位勢，都有一個明顯的簡併：假若波函數 $\psi\,\!$ 是某薛定諤方程式的解答，則其共軛函數 $\psi^*\,\!$ 也是這薛定諤方程式的解答。所以， $\psi\,\!$ 的實值部分或虛值部分，都分別是解答。我們只需要專注實值的波函數解答。這限制並不會影響到整個不含時問題。
轉移焦點到含時薛定諤方程式，兩個複共軛的波，以相反方向移動。給予某含時薛定諤方程式的解答 $\Psi(x,\,t)\,\!$ 。其替代波函數是另外一個解答：

$\Psi(x,\,t) \rightarrow \Psi^*(x,\, - t)\,\!$ 。

這解答是複共軛對稱性的延伸。稱複共軛對稱性為時間反轉。

[编辑] 么正性

在量子力學裏，對於任何事件，所有可能產生的結果的機率總和等於 1 ，稱這特性為么正性。薛定諤方程式能夠自動地維持么正性。

Difference of two squares

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (December 2009)

It has been suggested that Conjugate (algebra) be merged into this article or section. (Discuss) Proposed since January 2012.

In mathematics, the difference of two squares, or the difference of perfect squares, is a squared (multiplied by itself) number subtracted from another squared number. It refers to the identity

$a^2-b^2 = (a+b)(a-b)\,\!$

in elementary algebra.

[hide]

[edit] Proof

The proof is straightforward. Starting from the right-hand side, apply the distributive law to get

$(a+b)(a-b) = a^2+ba-ab-b^2\,\!$ ,

and set

$ba - ab = 0\,\!$

as an application of the commutative law. The resulting identity is one of the most commonly used in mathematics. Among many uses, it gives a simple proof of the AM–GM inequality in two variables.
The proof just given indicates the scope of the identity in abstract algebra: it will hold in any commutative ring R.
Conversely, if this identity holds in a ring R for all pairs of elements a and b of the ring, then R is commutative. To see this, we apply the distributive law to the right-hand side of the original equation and get

$a^2 + ba - ab - b^2\,\!$

and for this to be equal to $a^2 - b^2$ , we must have

$ba - ab = 0\,\!$

for all pairs a, b of elements of R, so the ring R is commutative.

[edit] Geometrical demonstrations

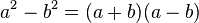
The difference of two squares can also be illustrated geometrically as the difference of two square areas in a plane. In the diagram, the shaded part represents the difference between the areas of the two squares, i.e. $a^2 - b^2$ . The area of the shaded part can be found by adding the areas of the two rectangles; $a(a-b) + b(a-b)$ , which can be factorized to $(a+b)(a-b)$ . Therefore $a^2 - b^2 = (a+b)(a-b)$
Another geometric proof proceeds as follows: We start with the figure shown in the first diagram below, a large square with a smaller square removed from it. The side of the entire square is a, and the side of the small removed square is b. The area of the shaded region is $a^2-b^2$ . A cut is made, splitting the region into two rectangular pieces, as shown in the second diagram. The larger piece, at the top, has width a and height a-b. The smaller piece, at the bottom, has width a-b and height b. Now the smaller piece can be detached, rotated, and placed to the right of the larger piece. In this new arrangement, shown in the last diagram below, the two pieces together form a rectangle, whose width is $a+b$ and whose height is $a-b$ . This rectangle's area is $(a+b)(a-b)$ . Since this rectangle came from rearranging the original figure, it must have the same area as the original figure. Therefore, 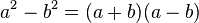$a^2-b^2 = (a+b)(a-b)$ .Any odd number can be expressed as difference of two squares.

Difference of two squares geometric proof.png

[edit] Uses

[edit] Complex number case: sum of two squares

The difference of two squares is used to find the linear factors of the sum of two squares, using complex number coefficients.
For example, the root of $z^2 + 5\,\!$ can be found using difference of two squares:

$z^2 + 5\,\!$

$= z^2 - (\sqrt{-5})^2$

$= z^2 - (i\sqrt5)^2$

$= (z + i\sqrt5)(z - i\sqrt5)$

Therefore the linear factors are $(z + i\sqrt5)$ and $(z - i\sqrt5)$ .
Since the two factors found by this method are Complex conjugates, we can use this in reverse as a method of multiplying a complex number to get a real number. This is used to get real denominators in complex fractions.^[1]

[edit] Rationalising denominators

The difference of two squares can also be used in the rationalising of irrational denominators.^[2] This is a method for removing surds from expressions (or at least moving them), applying to division by some combinations involving square roots.
For example: The denominator of $\dfrac{5}{\sqrt{3} + 4}\,\!$ can be rationalised as follows:

$\dfrac{5}{\sqrt{3} + 4}\,\!$

$= \dfrac{5}{\sqrt{3} + 4} \times \dfrac{\sqrt{3} - 4}{\sqrt{3} - 4}\,\!$

$= \dfrac{5(\sqrt{3} - 4)}{(\sqrt{3} + 4)(\sqrt{3} - 4)}\,\!$

$= \dfrac{5(\sqrt{3} - 4)}{\sqrt{3}^2 - 4^2}\,\!$

$= \dfrac{5(\sqrt{3} - 4)}{3 - 16}\,\!$

$= -\dfrac{5(\sqrt{3} - 4)}{13}.\,\!$

Here, the irrational denominator $\sqrt{3} + 4\,\!$ has been rationalised to $13\,\!$ . Any odd number can be expressed as difference of two squares.

[edit] Mental Arithmetic

The difference of two squares can also be used as a arithmetical short cut. If you are multiplying two numbers whose average is a number which is easily squared the difference of two squares can be used to give you the product of the original two numbers.
For example: $27 \times 33 = (30 - 3)(30 + 3)$
Which means using the difference of two squares $27 \times 33$ can be restated as
$a^2 - b^2$ which is $30^2 - 3^2 = 891$ .

[edit] Generalizations

Vectors

a

(purple),

b

(cyan) and

a + b

(blue) are shown with arrows

The identity also holds in inner product spaces over the field of real numbers, such as for dot product of Euclidean vectors:

${\mathbf a}\cdot{\mathbf a} - {\mathbf b}\cdot{\mathbf b} = ({\mathbf a}+{\mathbf b})\cdot({\mathbf a}-{\mathbf b})\,\!$

The proof is identical. By the way, assuming that

a

and

b

have equal norms (which means that their dot squares are equal), it demonstrates analytically the fact that two diagonals of a rhombus are perpendicular.

[edit] See also

Conjugate (algebra)

平方差

维基百科，自由的百科全书

跳转至：导航、搜索

平方差公式是數學公式的一種，它屬於乘法公式、因式分解及恆等式，被普遍使用。平方差指一個平方數或正方形，減去另一個平方數或正方形得來的乘法公式：

$a^2-b^2 \equiv \left(a+b\right)\left(a-b\right)$

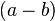$(a+b)$ 及 $(a-b)$ 的排列並不重要，可隨意排放。

phymath999