柯西-黎曼方程[编辑]
维基百科,自由的百科全书
复分析中的柯西-黎曼微分方程是提供了可微函数在开集中全纯函数的充要条件的两个偏微分方程,以柯西和黎曼得名。这个方程组最初出现在达朗贝尔的著作中。后来欧拉将此方程组和解析函数联系起来。 然后柯西采用这些方程来构建他的函数理论。黎曼关于此函数理论的论文于1851年问世。
在一对实值函数u(x,y)和v(x,y)上的柯西-黎曼方程组包括两个方程:
 ,
, 。该形式的矩阵是复数的矩阵表示。几何上,这样的一个矩阵总是一个旋转和一个缩放的复合,从而是保角(保持角度不变)的。因此,满足柯西-黎曼方程的有非零导数的函数保持平面曲线的角度不变。也即,柯西-黎曼方程是函数成为共形映射的条件。
。该形式的矩阵是复数的矩阵表示。几何上,这样的一个矩阵总是一个旋转和一个缩放的复合,从而是保角(保持角度不变)的。因此,满足柯西-黎曼方程的有非零导数的函数保持平面曲线的角度不变。也即,柯西-黎曼方程是函数成为共形映射的条件。
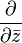 定义为
定义为
 。
。
。精确的讲,设
若该极限存在,则可以取h→0沿着实轴或者虚轴的极限;它在两种情况下应该给出同样的结果。从实轴逼近,得到
反过来,如果f:C → C作为映射到R2上的函数可微,则f复可微当且仅当柯西-黎曼方程成立。
在一对实值函数u(x,y)和v(x,y)上的柯西-黎曼方程组包括两个方程:
- (1a)

- (1b)
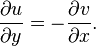
目录
[隐藏]注释和其他表述[编辑]
共形映射[编辑]
柯西-黎曼方程常常表述为其他形式。首先,它们可以写成复数形式:- (2)
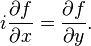
 ,
, 。该形式的矩阵是复数的矩阵表示。几何上,这样的一个矩阵总是一个旋转和一个缩放的复合,从而是保角(保持角度不变)的。因此,满足柯西-黎曼方程的有非零导数的函数保持平面曲线的角度不变。也即,柯西-黎曼方程是函数成为共形映射的条件。
。该形式的矩阵是复数的矩阵表示。几何上,这样的一个矩阵总是一个旋转和一个缩放的复合,从而是保角(保持角度不变)的。因此,满足柯西-黎曼方程的有非零导数的函数保持平面曲线的角度不变。也即,柯西-黎曼方程是函数成为共形映射的条件。复共轭的独立性[编辑]
方程组有时也被写作一个方程- (3)

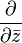 定义为
定义为 。
。复可微性[编辑]
柯西-黎曼方程是函数的复可微性(或称全纯性)的充要条件(Ahlfors 1953,§1.2)。精确的讲,设
若该极限存在,则可以取h→0沿着实轴或者虚轴的极限;它在两种情况下应该给出同样的结果。从实轴逼近,得到
反过来,如果f:C → C作为映射到R2上的函数可微,则f复可微当且仅当柯西-黎曼方程成立。
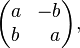



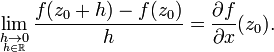
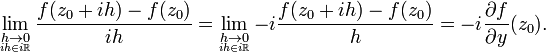

No comments:
Post a Comment