博弈论（Game theory），有时也称为对策论，或者赛局理论，应用数学的一个分支，目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。主要研究公式化了的激励结构（游戏或者博弈）间的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。也是运筹学的一个重要学科。
概述
概述
博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。表面上不同的相互作用可能表现出相似的激励结构(incentive structure)，所以他们是同一个游戏的特例。其中一个有名有趣的应用例子是囚徒困境。
具有竞争或对抗性质的行为成为博弈行为。在这类行为中，参加斗争或竞争的各方各自具有不同的目标或利益。为了达到各自的目标和利益，各方必须考虑对手的各种可能的行动方案，并力图选取对自己最为有利或最为合理的方案。比如日常生活中的下棋，打牌等。博弈论就是研究博弈行为中斗争各方是否存在着最合理的行为方案，以及如何找到这个合理的行为方案的数学理论和方法。
生物学家使用博弈理论来理解和预测进化（论）的某些结果。例如，John Maynard Smith 和George R. Price 在1973年发表于《自然》杂志上的论文中提出的“evolutionarily stable strategy”的这个概念就是使用了博弈理论。还可以参见进化博弈理论（evolutionary game theory）和行为生态学（behavioral ecology）。
数学定义
范式博弈
范式博弈又被译为正则形式的博弈、策略型赛局或标准型赛局。
是一个“参与者”(players)的集合。对于每一个“参与者”
. 博弈（游戏）是一个
也就是说，如果我们知道了参与者的策略集合是什么，那么就可以有一个实数值与之对应。 我们可以把上面的方程拆成两个方程来进一步把它一般化。一个方程是正则形式(Normal form game)的参与者程，描述策略规定结果的方式。 另外一个方程描写参与者对于结果(outcome)集合的偏好(preference)。也就是：
这里 
是游戏（博弈）的结果集合(outcome set)。对于每一个参与者
都有一个偏好函数( preference function)
是游戏（博弈）的结果集合(outcome set)。对于每一个参与者 都有一个偏好函数( preference function)
.- 展开形式的博弈
- 展开形式的博弈又可译为扩展形式的博弈、扩展式赛局或扩展型赛局。正则形式的定义为数学家们提供了“均衡”(equilibria)问题的研究一个容易使用的表达式。因为它避免了怎么计算“策略”的问题，也就是说游戏是怎么进行的问题。若要考虑游戏是如何进行的，展开形式的博弈是一个比较方便的表达式。这个形式与组合博弈论关系密切。这个定义通过一个树的形式给定。在树的每一个节点（vertex），不同的参与者选择一个边（edge）。纳什均衡如果某情况下无一参与者可以独自行动而增加收益，则此策略组合被称为纳什均衡点。例子其经典的例子就是囚徒困境。囚徒困境是一个非零和博弈。 大意是：一个案子的两个嫌疑犯被分开审讯，警官分别告诉两个囚犯，如果你招供，而对方不招供，则你将被立即释放，而对方将被判刑十年；如果两人均招供，将均被判刑两年。如果两人均不招供，将最有利，只被判刑半年。 于是，两人同时陷入招供还是不招供的两难处境。 但两人无法沟通，于是从各自的利益角度出发，都依据各自的理性而选择了招供， 这种情况就称为纳氏均衡点。 这时，个体的理性利益选择是与整体的理性利益选择不一致的。
囚犯甲的博弈矩阵 囚犯甲 招供 不招供 囚犯乙 招供 各判刑两年 甲判刑十年,乙立即释放 不招供 甲立即释放,乙判刑十年 各判刑半年 基于经济学中“理性经济人”的前提假设，两个囚犯符合自己利益的选择是坦白招供，原本对双方都有利的策略不招供从而均被判刑半年就不会出现。事实上，这样两人都选择坦白的策略以及因此被判两年的结局被称作是“纳什均衡”（也叫非合作均衡），换言之，在此情况下，无一参与者可以“独自行动”（即单方面改变决定）而增加收获。
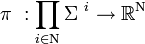
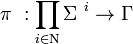
No comments:
Post a Comment