幾何與拓樸簡介
十月 7, 2011
學數學很多人都會迷失於符號與定理中。一開始數學在發展的時候,都是以相當容易理解的想法去做定義。大家或許會被這些專有名詞給嚇到了,千萬別害怕,我舉幾個例子,大家就會知道,數學其實有他簡單的概念在。幾個例子來說,何謂黎曼面?如果要以很好聽的數學術語來講,其定義為:一維的複流形。單從字面上來看,你大概不太能夠體會黎曼面是甚麼。而學數學的過程裡,你依然會遇到許多奇奇怪怪的術語。數學要用例子去看。
舉個高中生也能懂得例子,球面二維球面 就是最簡單的黎曼面。它是緊致可定向的幾何空間。但如果以高中生能懂得話來說呢?很簡單,所謂的緊致就是一個封閉的有界集合。所謂的有界,就是他是有範圍的。所謂的封閉,就是取球面上的點,不管怎麼跑,都還是會落在這個球面上(除非有外力)。所謂的曲面,請各位回想一下地球,是不是在地球的表面上,你會覺得自己是在平面,不是在彎曲的球上呢?(除了你搭外太空船,或者是到101大樓上去,才發現原來地球是彎曲的)。所以我們定義了(二維)曲面:假想人是活在這個世界上,會覺得自己是在平坦的空間中,但實際上 並不是,他是很多個平坦的平面黏貼起來的。這樣的空間會有座標的概念。舉例來說,我們有經度跟緯度。經度跟緯度就是一種座標呀!
就是最簡單的黎曼面。它是緊致可定向的幾何空間。但如果以高中生能懂得話來說呢?很簡單,所謂的緊致就是一個封閉的有界集合。所謂的有界,就是他是有範圍的。所謂的封閉,就是取球面上的點,不管怎麼跑,都還是會落在這個球面上(除非有外力)。所謂的曲面,請各位回想一下地球,是不是在地球的表面上,你會覺得自己是在平面,不是在彎曲的球上呢?(除了你搭外太空船,或者是到101大樓上去,才發現原來地球是彎曲的)。所以我們定義了(二維)曲面:假想人是活在這個世界上,會覺得自己是在平坦的空間中,但實際上 並不是,他是很多個平坦的平面黏貼起來的。這樣的空間會有座標的概念。舉例來說,我們有經度跟緯度。經度跟緯度就是一種座標呀!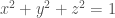 就可以用經度跟緯度去描述的。
就可以用經度跟緯度去描述的。
如果大家被數學名詞嚇到了,肯定看不出他好玩的地方在哪。在相對論中,協變微分這個名字很嚇人呀!但是,各位,千萬別害怕。我用很簡單的方式跟各位介紹。我們還是回到地球的例子。我們在地球上所做的一切運動都是內在的(除非利用了能源,用了太空船),一般的跑步,運動都是內在的行為。所謂的不是內在的,就是利用太空船或其他力量離開地球表面的活動。所以,只要一直在地球表面活動而不離開地球表面,我們都稱為內在。協變微分更好玩。微分就是研究變化率的一個方法,所謂的協變微分,講的就是內在的微分。也就是說,研究一切在地球表面上的變化,就可稱為協變微分。如果脫離了地球,就不是協變微分。
在打個比方,代數拓樸中的同調群,其實可以用高中生就能懂得方法可以解釋。因為發明同調群的人,想法是相當簡單的。記得以前高中還有所謂的補充教材。裡面有提了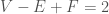 。
。 是頂點,
是頂點,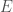 是邊,
是邊, 是面的數量。這是著名的由拉公式(Euler formula)。
是面的數量。這是著名的由拉公式(Euler formula)。
同調群,便是去計算一些多邊形或多面體的"點,線,面"的一些數量所產生的東西。進而去計算更一般的集合(或所謂的拓樸空間)。我們可以把球面用三角形的方式填出來。(當然這三角形並不一定是直線構成的,是曲線。)這是所謂的三角剖分(Triangulation)。同調群就是透過三角剖分所定義出來的量。
打個比方,三角形 是由點
是由點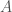 ,
, 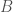 ,
, 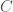 與邊
與邊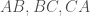 所構成。考慮任意的整數
所構成。考慮任意的整數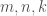 我們會考慮
我們會考慮 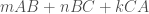 的組合(稱為一個鏈chain)。我們可以定義邊長的邊界映射
的組合(稱為一個鏈chain)。我們可以定義邊長的邊界映射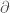 ,檢而言之,任意向量
,檢而言之,任意向量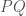 ,其邊界映射為
,其邊界映射為
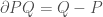
其實就是把向量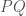 送到他的邊界,邊界就是頂點
送到他的邊界,邊界就是頂點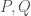 。(這是高二數學對吧)所以任意一個鍊的邊界會長怎樣呢?
。(這是高二數學對吧)所以任意一個鍊的邊界會長怎樣呢?
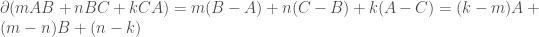
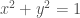 ,在平面上為一個圓。在此圓上任取三個點
,在平面上為一個圓。在此圓上任取三個點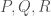 我們有
我們有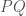 弧,
弧,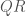 弧
弧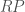 弧。一樣可以定義
弧。一樣可以定義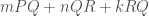 。去計算一些數。我們發現,圓的同調群一樣也是正整數。所以我們會去思考,圓跟三角形是不是有某種關係呢?講個數學的術語:圓與三角形同胚。(其實是由同胚得到同調群相等。)所謂的拓樸就是在研究集合之間的關係。看似不同的兩個東西,在某種"結構"上是相同的。所以拓樸主要是在分類不同的空間關係。
。去計算一些數。我們發現,圓的同調群一樣也是正整數。所以我們會去思考,圓跟三角形是不是有某種關係呢?講個數學的術語:圓與三角形同胚。(其實是由同胚得到同調群相等。)所謂的拓樸就是在研究集合之間的關係。看似不同的兩個東西,在某種"結構"上是相同的。所以拓樸主要是在分類不同的空間關係。
舉個高中生也能懂得例子,球面二維球面
如果大家被數學名詞嚇到了,肯定看不出他好玩的地方在哪。在相對論中,協變微分這個名字很嚇人呀!但是,各位,千萬別害怕。我用很簡單的方式跟各位介紹。我們還是回到地球的例子。我們在地球上所做的一切運動都是內在的(除非利用了能源,用了太空船),一般的跑步,運動都是內在的行為。所謂的不是內在的,就是利用太空船或其他力量離開地球表面的活動。所以,只要一直在地球表面活動而不離開地球表面,我們都稱為內在。協變微分更好玩。微分就是研究變化率的一個方法,所謂的協變微分,講的就是內在的微分。也就是說,研究一切在地球表面上的變化,就可稱為協變微分。如果脫離了地球,就不是協變微分。
在打個比方,代數拓樸中的同調群,其實可以用高中生就能懂得方法可以解釋。因為發明同調群的人,想法是相當簡單的。記得以前高中還有所謂的補充教材。裡面有提了
同調群,便是去計算一些多邊形或多面體的"點,線,面"的一些數量所產生的東西。進而去計算更一般的集合(或所謂的拓樸空間)。我們可以把球面用三角形的方式填出來。(當然這三角形並不一定是直線構成的,是曲線。)這是所謂的三角剖分(Triangulation)。同調群就是透過三角剖分所定義出來的量。
打個比方,三角形
其實就是把向量
如果把邊界送到原點(各位同學可以想一下三個點連線出來剛好是原點是有意義的吧!),我們發現 k=m=n。其實就是所謂的循環(cycle)。循環就長這樣: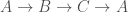 或者是
或者是 ,其中
,其中 是整數。所以三角形
是整數。所以三角形 的同調群是整數。
的同調群是整數。
取
今天的幾何與拓樸課程暫時上到這裡,有機會再繼續介紹吧!
No comments:
Post a Comment