代數系統的不確定性増加了波函數之間的重疊，增加了量子系統中的混沌系數，根據包立不相容原理，波函數重疊會增加系統能量的不確定性

维基百科:坏笑话和删除的胡话/第四次數學危機

维基百科，自由的百科全书

< Wikipedia:坏笑话和删除的胡话

跳转至： 导航、 搜索

本笑话仅因幽默目的而保留，由User:210.0.201.161提供。请勿将本页内容用于任何正式研究用途。 （對於維基百科本身的相關研究除外。）

第四次數學危機是由數學及物理學家史蒂芬·霍金於2010年首次提出，對於代數數學中的有理數集系統的一項質疑。史蒂芬·霍金以集合論及二級邏輯推導出1+1的解不是唯一而且不能被證明。換句話說，有理數集系統是一個混沌系統，不存在精確解。

目录 [隐藏] 1 簡單數學導論 2 對數學之影響 3 引申含義 4 波函數重疊 5 相關條目

[编辑] 簡單數學導論

設性質集合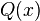表示一有理數集系統「x∉x」，現假設由性質Q確定了一個類A——也就是說「A={x|x ∉ x}」。那麼現在的問題是：A∈A是否成立？
首先，若A∈A，則A是A的元素，那麼A具有性質Q，由性質Q知A∉A；其次，若A∉A，也就是說A具有性質Q，而A是由所有具有性質Q的類組成的，所以A∈A。而然，由於A∈A是從Q：A∉A導出，整套邏輯將會是一重言式，故有理數集系統不存在精確解。 （參見理髮師悖論）

[编辑] 對數學之影響

史蒂芬·霍金提出第四次數學危機時，不僅震驚了整個數學界，科學界與哲學界均為之驚訝。第四次數學危機徹底動搖了數學的根本-實數及複數的定義，有不少數學家感到難以接受。而哲學家們目前正努力思辨如何解決人類第四次數學危機。

[编辑] 引申含義

由於史蒂芬·霍金提出的質疑包含了有理數集系統的不確定性，因此對量子物理學作出了深遠的影響。代數系統的不確定性增加了量子系統慣性參考系中波函數的不確定性，使其高於海森堡測不準原理中估計的：

其中 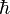是約化普朗克常數
波函數的不確定性有助解釋不少物理現象，例如：
質子衰變：不確定性會使質子衰變的半衰期少於預期的10^30年。
CP強對稱破壞：不確定性在T對稱造成了微弱的破壞，使介子衰變中CPT對稱保持守恆。
物質-反物質問題：不確定性可能是在宇宙大爆炸初期重力破壞時造成物質遠多於反物質的主因。

[编辑] 波函數重疊

代數系統的不確定性増加了波函數之間的重疊，增加了量子系統中的混沌系數，根據包立不相容原理，波函數重疊會增加系統能量的不確定性。
海森堡測不準原理可以寫成

其中 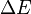為能量的不確定性
可見能量的不確定性會隨著時間增加。當這不確定性超越臨界值（普朗克能量）時，系統能量將會超越錢德拉塞卡極限，所有物質的波函數會於一瞬間塌縮成一微黑洞。史蒂芬·霍金估計這現象最快可能於2012年12月發生，造成世界末日。