只有平方反比連心勢 (
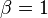 ) 與徑向諧振子勢 (
) 與徑向諧振子勢 ( )能夠造成穩定的,閉合的,非圓形的公轉軌道。
)能夠造成穩定的,閉合的,非圓形的公轉軌道。牛頓旋轉軌道定理[编辑]
牛頓旋轉軌道定理表明,對於一個感受到線性作用力或平方反比作用力的移動中的粒子,假設再增添立方反比力於此粒子,只要因子 是有理數,則粒子的軌道仍舊是閉合軌道。根據牛頓旋轉軌道定理的方程式,增添的立方反比力
是有理數,則粒子的軌道仍舊是閉合軌道。根據牛頓旋轉軌道定理的方程式,增添的立方反比力  為
為 ;
;
 是粒子原本的角動量,
是粒子原本的角動量, 是粒子的質量。
是粒子的質量。所以,
 。
。由於
 是有理數,
是有理數, 可以寫為分數
可以寫為分數 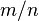 ;其中,
;其中, 和
和  都是整數。對於這案例,增添立方反比力使得粒子完成
都是整數。對於這案例,增添立方反比力使得粒子完成  圈公轉的時間等於原本完成
圈公轉的時間等於原本完成  圈公轉的時間。這種產生閉合軌道的方法不違背伯特蘭定理,因為,增添的立方反比力與粒子的原本角動量有關。
圈公轉的時間。這種產生閉合軌道的方法不違背伯特蘭定理,因為,增添的立方反比力與粒子的原本角動量有關。
Take the 2-minute tour ×
Physics Stack Exchange is a question and answer site for active researchers, academics and students of physics. It's 100% free, no registration required.
I have heard from here that stable orbits (ones that require a large amount of force to push it significantly out of it's elliptical path) can only exist in a three spatial dimensions because gravity would operate differently in a two or four dimensional space. Why is this?
| ||||
Specifically what that is referring to is the 'inverse-square law', nature of the gravitational force, i.e. the force of gravity is inversely proportional to the square of the distance:
If you expand this concept to that of general power-law forces (e.g. when you're thinking about the virial theorem), you can write: Stable orbits are only possible for a few, special values of the exponent ' Now, what does that have to do with spatial dimensions? Well, it turns out that in a more accurate description of gravity (in particular, general relativity) the exponent of the power-law ends up being one-less than the dimension of the space. For example, if space were 2-dimensional, then the force would look like Note also that 1: A 'closed' orbit is one in which the particle returns to its previous position in phase space (i.e. its orbit repeats itself). | |||||||||||||||||||||
|
I'll try to answer it by considering radial deviations from a circular orbit. First we have to assume two things about our n-dimensional universe: Newton's second law still holds, that is,
for a particle's position vector in n-dimensions and also that the law of gravity is given by Gauss' law: The solution to that pde is Since the motion will always be constrained to move in the 2-plane spanned by the initial radial vector Now we make use of the fact that gravity is always radial, so For a circular orbit at Let's check this on a radial force So for dimensions cheers. | |||||
|
I assume this is talking about Newtonian gravity (i.e., not relativity). Let's consider the effective potential:
where This first term appears from the equations of motion for a free particle. Phrasing it in terms of angular momentum is convenient because under central forces, angular momentum is a conserved quantity. Why do we use the effective potential? Because it helps us talk solely about the radial motions of a particle, lumping the angular motions in with the real potential. A local extremum of the effective potential tells us about an equilibrium distance. Now, in 3d, the potential In 2d, the potential is different. Why is this? Newtonian gravity deals with differential equations of the form Let's check for a second that this is the case. Let which is inward for all positive for two constants So At Hm. That would suggest the equilibrium point is stable. So, perhaps someone has a reference to suggest this. I'm stuck. | |||
Not the answer you're looking for? Browse other questions tagged newtonian-gravity dimensions orbital-motion stability or ask your own question.
tagged
asked
|
11 months ago
|
viewed
|
1365 times
|
active
|
Community Bulletin
Hot Network Questions
- Produce the number 2014 without any numbers in your source code
- Making these conditions shorter
- At what point is version control needed?
- Do we know if there exist true mathematical statements that can not be proven?
- Verify Brainfuck program
- How to trigger a system self destruct with a certain password is entered
- What kinds of encryption are _not_ breakable via Quantum Computers?
- Battle system in C++
- Why do people say that Peter Jackson can not make LOTR/Hobbit sequels?
- I need a program where the user inputs an array of doubles and the program outputs the array sorted
- Telling my manager that he made a huge budgeting mistake
- Proper procedure for leaving class D airspace?
- To write this norm equation better?
- Editor didn't invite for a second review
- Sort the distinct elements of a list in descending order by frequency
- Fourier - Are sinusoidals strictly required?
- Where does this part of RSA come from?
- How to parse ISO8601 dates with linux date command
- Teaching homology via everyday examples
- What are Harry Potter's Children?
- Idiom or word for a very crowded place
- Why JavaScript functions always return a value?
- What is the advantage of using the notation 'fig:' in the \label {}?
- What was Sherlock about to remark?
