或者只能說拉普拉斯轉換與線性變換
是積分變換而非微分算子,但它肯定是線性變換。事實是所有我們在大學裡學到的不管什麼XX變換都是線性變換。L變換屬於傅立葉變換家族的一員,常作為系統分析和公式推導之用。與矩陣運算有關係的是離散傅立葉轉換,其用途在訊號處理
從線性代數看微分方程
本文的閱讀等級:中級
大學理工科系經常將微分方程和線性代數分為兩門獨立課程講授,表面上兩者處理的問題對象不同,使用的分析運算技巧也相異,在這種認知下,我們很自然會將微分方程和線性代數看成平行進展的數學領域。抱持懷疑態度的學生可能發現兩者間存在一些概念和形式交集,例如,微分方程與線性代數都有特徵方程式 (characteristic equation) 一詞,難免心中納悶:究竟微分方程和線性代數有什麼關係?對多數人來說,這並不是一個顯而易見的問題,我也不認為可以三言兩語就說清楚。以下我選擇幾個重要的線性代數主題──線性函數、零空間、特徵值和特徵向量,以及齊次和非齊次方程,從這些角度檢視微分方程與線性代數的關連。開始之前,如果讀者還不能接受函數也是向量這個觀念,請先閱讀“從幾何向量空間到函數空間”。
1. 線性函數
設 是由向量空間
是由向量空間 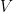 映射至另一向量空間
映射至另一向量空間 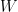 的函數,標記為
的函數,標記為  。對於
。對於 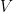 裡的任意向量
裡的任意向量  和
和 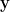 ,以及任意實數
,以及任意實數  ,如果總是滿足
,如果總是滿足
 我們稱
我們稱  是線性函數,也稱為線性算子、線性映射或線性變換,之所以有這些不同的名稱是為了配合強調
是線性函數,也稱為線性算子、線性映射或線性變換,之所以有這些不同的名稱是為了配合強調  的具體作用。
的具體作用。
下面我們看幾個建立於具有實際用途的向量空間的線性函數。
1A. 幾何向量空間
設 是
是 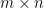 階實矩陣,
階實矩陣, ,
, 是一個由
是一個由 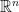 映至
映至  的線性函數,執行矩陣乘法計算可以確認
的線性函數,執行矩陣乘法計算可以確認

1B. 多項式空間
令 為所有多項式形成的向量空間,微分算子
為所有多項式形成的向量空間,微分算子  可視為由
可視為由  映至
映至  的函數,例如,
的函數,例如, 。微分算子
。微分算子 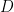 是一個線性函數,利用導數基本性質可知
是一個線性函數,利用導數基本性質可知
 求導兩次可記為
求導兩次可記為  ,不難檢查
,不難檢查  是線性函數,推廣至更高次冪,
是線性函數,推廣至更高次冪,  全部都是線性函數。
全部都是線性函數。
1C. 連續實函數空間
令 表示所有連續實函數形成的空間,設
表示所有連續實函數形成的空間,設  ,對於
,對於  ,
, ,考慮以下的例子:
,考慮以下的例子:

 是線性函數,因為
是線性函數,因為
 將微分算子
將微分算子 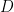 與線性函數
與線性函數  結合成一條方程式便得到微分方程
結合成一條方程式便得到微分方程
 例如,設
例如,設  ,
, ,就有
,就有  或寫為
或寫為  。求解微分方程等於尋找
。求解微分方程等於尋找 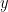 使得
使得  ,這是一個相當重要的觀念,由此可以逐步建立微分方程與線性代數的關連性。
,這是一個相當重要的觀念,由此可以逐步建立微分方程與線性代數的關連性。
2. 零空間
設 是一個線性函數,所有滿足
是一個線性函數,所有滿足  的
的  所形成的集合構成
所形成的集合構成 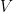 裡的一個子空間,稱為零空間 (nullspace) 或核 (kernel),記作
裡的一個子空間,稱為零空間 (nullspace) 或核 (kernel),記作  或
或  。設
。設  ,利用線性函數的基本性質,就有
,利用線性函數的基本性質,就有
 以上二式指出
以上二式指出  滿足向量加法和純量乘法封閉性,所以確定
滿足向量加法和純量乘法封閉性,所以確定  是
是 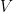 裡的子空間。
裡的子空間。
計算零空間的條件式 稱為齊次方程 (homogeneous equation),辨識特點是等號右側為零。齊次線性方程至少有一零解,
稱為齊次方程 (homogeneous equation),辨識特點是等號右側為零。齊次線性方程至少有一零解, ,也就是說零空間
,也就是說零空間  必定包含零向量,理由如下:
必定包含零向量,理由如下:  ,或者
,或者  。經常我們有興趣知道除了平凡解
。經常我們有興趣知道除了平凡解  之外,零空間是否尚包含非零向量,原因是這能讓我們檢查線性函數
之外,零空間是否尚包含非零向量,原因是這能讓我們檢查線性函數  是否為一對一 (one-to-one)。函數
是否為一對一 (one-to-one)。函數  稱為一對一,若
稱為一對一,若  僅發生於
僅發生於  。對於線性函數
。對於線性函數  ,有這個性質:
,有這個性質: 是一對一,若
是一對一,若  的零空間僅包含零向量
的零空間僅包含零向量  ,反向陳述也為真。
,反向陳述也為真。
很明顯,連續實函數空間 有無限維,因此沒有如
有無限維,因此沒有如 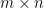 階矩陣那般有四個基本子空間的分析平台 (參見“線性代數基本定理 (二)”),但建立於
階矩陣那般有四個基本子空間的分析平台 (參見“線性代數基本定理 (二)”),但建立於  之上的線性函數
之上的線性函數  仍然有定義良好的零空間
仍然有定義良好的零空間  與值域 (range)
與值域 (range)  ,詳細請見“線性代數基本定理 (一)”。
,詳細請見“線性代數基本定理 (一)”。
下面我們探討幾個常見的線性函數的零空間。
2A. 齊次線性聯立方程
考慮以下齊次線性聯立方程
 或改寫為矩陣形式表示的線性方程:
或改寫為矩陣形式表示的線性方程:
![f(\mathbf{x})=A\mathbf{x}=\left[\!\!\begin{array}{crr} 1&1&-1\\ 1&-1&1 \end{array}\!\!\right]\begin{bmatrix} x\\ y\\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0 \end{bmatrix} f(\mathbf{x})=A\mathbf{x}=\left[\!\!\begin{array}{crr} 1&1&-1\\ 1&-1&1 \end{array}\!\!\right]\begin{bmatrix} x\\ y\\ z \end{bmatrix}=\begin{bmatrix} 0\\ 0 \end{bmatrix}](http://s0.wp.com/latex.php?latex=f%28%5Cmathbf%7Bx%7D%29%3DA%5Cmathbf%7Bx%7D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcrr%7D++++1%261%26-1%5C%5C++++1%26-1%261++++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cbegin%7Bbmatrix%7D++++x%5C%5C++++y%5C%5C++++z++++%5Cend%7Bbmatrix%7D%3D%5Cbegin%7Bbmatrix%7D++++0%5C%5C++++0++++%5Cend%7Bbmatrix%7D&bg=ffffff&fg=000000&s=0) 利用高斯消去法求出齊次解
利用高斯消去法求出齊次解  ,
,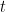 為任意實數,也就是說
為任意實數,也就是說  的零空間由向量
的零空間由向量  擴張而成,零空間
擴張而成,零空間  與其表示矩陣
與其表示矩陣  的零空間
的零空間  指的是同一回事。
指的是同一回事。
2B. 微分算子
將微分算子 施行於
施行於  ,
,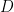 的零空間包含所有一次導數為零之實函數,由導數基本性質可知
的零空間包含所有一次導數為零之實函數,由導數基本性質可知  是一個包含所有常數函數
是一個包含所有常數函數  的子空間。
的子空間。
2C. 齊次微分方程
考慮下面的常係數齊次微分方程
 也可以用微分算子表示為
也可以用微分算子表示為
 線性算子的線性組合仍為線性算子,所以
線性算子的線性組合仍為線性算子,所以  也是線性的。求解齊次微分方程
也是線性的。求解齊次微分方程  等於是計算
等於是計算  的零空間。下面將詳細說明求解齊次常係數微分方程的過程,在此先給出結果。線性算子
的零空間。下面將詳細說明求解齊次常係數微分方程的過程,在此先給出結果。線性算子  的零空間由線性獨立的函數
的零空間由線性獨立的函數 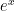 和
和  擴張而成,
擴張而成,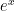 和
和  是零空間
是零空間  的基底函數,故齊次解為其線性組合
的基底函數,故齊次解為其線性組合  。從線性函數的角度,齊次解必定落在
。從線性函數的角度,齊次解必定落在  的零空間內,亦即
的零空間內,亦即

3. 特徵值與特徵向量
給定一線性變換 與向量
與向量  ,經常
,經常  和
和  沒有什麼簡單關係,但下面這種不改變向量方向的關係卻非常有用:
沒有什麼簡單關係,但下面這種不改變向量方向的關係卻非常有用:
 若
若  為非零向量,我們稱
為非零向量,我們稱  為
為  的特徵向量,而
的特徵向量,而 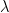 則稱為對應
則稱為對應  的特徵值。請特別注意,零向量不被視為特徵向量,既使對於任意線性變換
的特徵值。請特別注意,零向量不被視為特徵向量,既使對於任意線性變換  ,任何
,任何 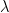 都滿足
都滿足  。但是我們接受特徵值為零的情況,只要存在
。但是我們接受特徵值為零的情況,只要存在  滿足
滿足 就行。很明顯地,若線性變換
就行。很明顯地,若線性變換  有零特徵值,則
有零特徵值,則  的零空間必定包含非零向量。這個結論非常的重要,請讀者弄清楚後再繼續往下閱讀。
的零空間必定包含非零向量。這個結論非常的重要,請讀者弄清楚後再繼續往下閱讀。
3A. 矩陣變換
設 為線性變換,以矩陣表示為
為線性變換,以矩陣表示為  。考慮下例,
。考慮下例, ,
,
 設
設 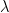 為
為  的特徵值滿足方程式
的特徵值滿足方程式  ,亦即
,亦即  ,因為我們要求特徵向量
,因為我們要求特徵向量  不得為零,矩陣
不得為零,矩陣  的零空間包含非零向量,推知
的零空間包含非零向量,推知  是不可逆的。由行列式性質,
是不可逆的。由行列式性質, ,將上例代入得到
,將上例代入得到  ,線性代數課本稱之為矩陣
,線性代數課本稱之為矩陣  的特徵方程式。由此可解出
的特徵方程式。由此可解出  有特徵值
有特徵值  ,對應的特徵向量分別為
,對應的特徵向量分別為 ![\left[\!\!\begin{array}{r} 4\\ -1 \end{array}\!\!\right] \left[\!\!\begin{array}{r} 4\\ -1 \end{array}\!\!\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++++4%5C%5C++++-1++++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0) ,
, 。注意,齊次方程
。注意,齊次方程  對應
對應  ,故特徵向量
,故特徵向量 ![\left[\!\!\begin{array}{r} 4\\ -1 \end{array}\!\!\right] \left[\!\!\begin{array}{r} 4\\ -1 \end{array}\!\!\right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Br%7D++++4%5C%5C++++-1++++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D&bg=ffffff&fg=000000&s=0) 擴張出
擴張出  的零空間。
的零空間。
3B. 微分算子
考慮以下微分算式: ,
, ,
, ,函數
,函數 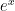 ,
, ,
, 是微分算子
是微分算子 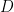 的特徵向量,對應的特徵值分別為
的特徵向量,對應的特徵值分別為 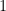 ,
,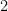 ,
,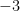 。繼續推廣,
。繼續推廣, 是任意數,
是任意數, ,得知
,得知  是
是  的特徵向量,對應的特徵值為
的特徵向量,對應的特徵值為  。
。
再考慮下面微分算子的線性組合:
 線性算子
線性算子  的特徵向量
的特徵向量 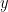 滿足
滿足  ,既然
,既然  有特徵向量
有特徵向量  ,不妨嘗試代入計算
,不妨嘗試代入計算
 我們發現
我們發現  的特徵向量也是
的特徵向量也是  ,對應的特徵值則為
,對應的特徵值則為  。
。
3C. 齊次微分方程
再次考慮上述常係數齊次微分方程,抄錄於下:
 或寫為
或寫為  ,前面說過求解齊次微分方程等於是計算
,前面說過求解齊次微分方程等於是計算  的零空間,也就是找出對應特徵值
的零空間,也就是找出對應特徵值  的特徵向量,如下:
的特徵向量,如下:
 因為
因為  ,必定有
,必定有  ,此即為微分方程教科書所稱的特徵方程式。解出
,此即為微分方程教科書所稱的特徵方程式。解出  ,特徵向量為
,特徵向量為 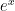 ,
, ,它們都對應特徵值
,它們都對應特徵值 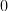 。我們得到一個重要的結論:求解齊次微分方程的本質就是問線性算子
。我們得到一個重要的結論:求解齊次微分方程的本質就是問線性算子  的那些特徵向量對應零特徵值。
的那些特徵向量對應零特徵值。
我猜想此處正是令莘莘學子困惑不已的地方,線性代數的特徵方程式是解出方陣 的特徵值所使用的條件式,而微分方程所稱的特徵方程式卻是線性微分算子
的特徵值所使用的條件式,而微分方程所稱的特徵方程式卻是線性微分算子  的特徵值
的特徵值  所必須要滿足的條件。這太奇怪了!怎麼可能兩者所稱的特徵方程式指的是不完全相同的事情?
所必須要滿足的條件。這太奇怪了!怎麼可能兩者所稱的特徵方程式指的是不完全相同的事情?
轉一個彎就可以看清原來微分方程和線性代數講的特徵方程式確實是同一個東西,關鍵在於將微分方程表示為線性系統。用上面的例子說明,令向量 ,齊次微分方程
,齊次微分方程  可用矩陣形式表示為
可用矩陣形式表示為
![\mathbf{u}'=\begin{bmatrix} y''\\ y' \end{bmatrix}=\left[\!\!\begin{array}{cr} 3&-2\\ 1&0 \end{array}\!\!\right]\begin{bmatrix} y'\\ y \end{bmatrix}=A\mathbf{u} \mathbf{u}'=\begin{bmatrix} y''\\ y' \end{bmatrix}=\left[\!\!\begin{array}{cr} 3&-2\\ 1&0 \end{array}\!\!\right]\begin{bmatrix} y'\\ y \end{bmatrix}=A\mathbf{u}](http://s0.wp.com/latex.php?latex=%5Cmathbf%7Bu%7D%27%3D%5Cbegin%7Bbmatrix%7D++++y%27%27%5C%5C++++y%27++++%5Cend%7Bbmatrix%7D%3D%5Cleft%5B%5C%21%5C%21%5Cbegin%7Barray%7D%7Bcr%7D++++3%26-2%5C%5C++++1%260++++%5Cend%7Barray%7D%5C%21%5C%21%5Cright%5D%5Cbegin%7Bbmatrix%7D++++y%27%5C%5C++++y++++%5Cend%7Bbmatrix%7D%3DA%5Cmathbf%7Bu%7D&bg=ffffff&fg=000000&s=0) 微分方程所說的齊次方程的特徵方程式
微分方程所說的齊次方程的特徵方程式  正是線性代數所說的齊次線性系統裡方陣
正是線性代數所說的齊次線性系統裡方陣  的特徵方程式
的特徵方程式
 請讀者計算
請讀者計算  的特徵向量並解釋其意義,這部份的工作就留給讀者朋友們自行發掘釐清。
的特徵向量並解釋其意義,這部份的工作就留給讀者朋友們自行發掘釐清。
4. 非齊次方程
考慮線性函數 的非齊次方程式
的非齊次方程式
 上式中我們假設
上式中我們假設  是
是  的值域
的值域  中的固定向量,因此保證必定存在解。在求非齊次方程式的通解時,函數
中的固定向量,因此保證必定存在解。在求非齊次方程式的通解時,函數  的零空間也扮演非常重要的角色。下面這個定理不僅適用於線性代數的聯立方程,也適用於線性微分方程,微分方程教科書通常叫它做疊加原理 (superposition principle):
的零空間也扮演非常重要的角色。下面這個定理不僅適用於線性代數的聯立方程,也適用於線性微分方程,微分方程教科書通常叫它做疊加原理 (superposition principle):
若 是線性方程
是線性方程  的某個合法解,稱為特解 (particular solution),則方程式可能的解所形成的集合稱為通解 (general solution,或一般解),它包含所有的
的某個合法解,稱為特解 (particular solution),則方程式可能的解所形成的集合稱為通解 (general solution,或一般解),它包含所有的  ,其中
,其中  為齊次方程
為齊次方程  的一解,稱為齊次解 (homogeneous solution)。
的一解,稱為齊次解 (homogeneous solution)。
證明非常簡單,假設 ,並有
,並有  ,因為
,因為  是線性函數,
是線性函數,
 可知
可知  ,
, 是零空間中的某一個向量,故
是零空間中的某一個向量,故  就是我們一心想得到的通解。
就是我們一心想得到的通解。
4A. 線性聯立方程
觀察以下的非齊次線性聯立方程
 不難得到一個特解
不難得到一個特解  ,對應的齊次方程解為
,對應的齊次方程解為  ,
,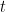 是任意實數,故通解可表示為
是任意實數,故通解可表示為  。
。
4B. 常係數微分方程
考慮這個非齊次微分方程
 將它以微分算子表示為
將它以微分算子表示為  。下面使用未定係數法求出特解,由於
。下面使用未定係數法求出特解,由於  ,對於任何解
,對於任何解  ,就有
,就有
 上式等於解一個新的齊次微分方程,所以任意特解必定有以下形式 (請讀者參閱手邊的微分方程教科書,建議閱讀“利用 Jordan form 解差分方程與微分方程”):
上式等於解一個新的齊次微分方程,所以任意特解必定有以下形式 (請讀者參閱手邊的微分方程教科書,建議閱讀“利用 Jordan form 解差分方程與微分方程”):
 由於前兩項即為齊次解,
由於前兩項即為齊次解, ,我們僅需專注於第 3 項,因此設
,我們僅需專注於第 3 項,因此設  。為求出
。為求出  ,可計算
,可計算
 一併代入原式,就有
一併代入原式,就有
 整理後得到
整理後得到  ,比較等號兩端係數於是解出
,比較等號兩端係數於是解出  ,故特解為
,故特解為  ,所以有通解
,所以有通解

最後我將本文推論得到的幾個觀念整理於下。常係數微分方程可以視為由線性微分算子 產生的方程式,
產生的方程式, ,其中
,其中  ,
, 是任意屬於
是任意屬於  的函數向量。求解齊次微方方程
的函數向量。求解齊次微方方程  的實際作用就是計算線性算子
的實際作用就是計算線性算子  的零空間,亦即計算線性算子
的零空間,亦即計算線性算子  的那些特徵向量對應零特徵值。如果又將
的那些特徵向量對應零特徵值。如果又將  改寫為齊次線性系統
改寫為齊次線性系統  ,
,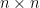 階常係數矩陣
階常係數矩陣  的特徵方程式就是我們在微分方程裡看到的同一條式子
的特徵方程式就是我們在微分方程裡看到的同一條式子  。撇開微分方程底下偽裝的線性變換、零空間和通解的結構,僅就特徵方程式而言,微分方程與線性代數確實有著密切的關係。
。撇開微分方程底下偽裝的線性變換、零空間和通解的結構,僅就特徵方程式而言,微分方程與線性代數確實有著密切的關係。
大學理工科系經常將微分方程和線性代數分為兩門獨立課程講授,表面上兩者處理的問題對象不同,使用的分析運算技巧也相異,在這種認知下,我們很自然會將微分方程和線性代數看成平行進展的數學領域。抱持懷疑態度的學生可能發現兩者間存在一些概念和形式交集,例如,微分方程與線性代數都有特徵方程式 (characteristic equation) 一詞,難免心中納悶:究竟微分方程和線性代數有什麼關係?對多數人來說,這並不是一個顯而易見的問題,我也不認為可以三言兩語就說清楚。以下我選擇幾個重要的線性代數主題──線性函數、零空間、特徵值和特徵向量,以及齊次和非齊次方程,從這些角度檢視微分方程與線性代數的關連。開始之前,如果讀者還不能接受函數也是向量這個觀念,請先閱讀“從幾何向量空間到函數空間”。
1. 線性函數
設
下面我們看幾個建立於具有實際用途的向量空間的線性函數。
1A. 幾何向量空間
設
1B. 多項式空間
令
1C. 連續實函數空間
令
2. 零空間
設
計算零空間的條件式
很明顯,連續實函數空間
下面我們探討幾個常見的線性函數的零空間。
2A. 齊次線性聯立方程
考慮以下齊次線性聯立方程
2B. 微分算子
將微分算子
2C. 齊次微分方程
考慮下面的常係數齊次微分方程
3. 特徵值與特徵向量
給定一線性變換
3A. 矩陣變換
設
3B. 微分算子
考慮以下微分算式:
再考慮下面微分算子的線性組合:
3C. 齊次微分方程
再次考慮上述常係數齊次微分方程,抄錄於下:
我猜想此處正是令莘莘學子困惑不已的地方,線性代數的特徵方程式是解出方陣
轉一個彎就可以看清原來微分方程和線性代數講的特徵方程式確實是同一個東西,關鍵在於將微分方程表示為線性系統。用上面的例子說明,令向量
4. 非齊次方程
考慮線性函數
若
證明非常簡單,假設
4A. 線性聯立方程
觀察以下的非齊次線性聯立方程
4B. 常係數微分方程
考慮這個非齊次微分方程
最後我將本文推論得到的幾個觀念整理於下。常係數微分方程可以視為由線性微分算子
9 則回應給 從線性代數看微分方程
發表迴響
%d bloggers like this:



Laplace Transformation 可以說是一種「線性微分算子」的運作嗎?
或者只能說拉普拉斯轉換與線性變換,有點類似而已?
不能化作矩陣運算?
假如可以化為矩陣,要如何作?
也許上面的問題有點幼稚,但我基於好奇心而發問。1989年我修完大一微積分之後,學校再也沒有相關課程,買書自學微分方程,只懂得粗淺概念,例題幾乎沒作過。
現在看周老師的DVD,看到Lecture 7-1,越來越精彩,可是我對例題仍無興趣,因為我不必準備考試。但是其中的思考邏輯,我覺得可以應用在很多方面,收穫良多。
逆變換為
可見L變換是積分變換而非微分算子,但它肯定是線性變換。事實是所有我們在大學裡學到的不管什麼XX變換都是線性變換。L變換屬於傅立葉變換家族的一員,常作為系統分析和公式推導之用。與矩陣運算有關係的是離散傅立葉轉換,其用途在訊號處理。
對於L變換的應用,解出微分方程的答案,
我們可否說它是「轉到另一個向量空間,作一些處理,再轉換回到原來的向量空間」?
或者,應該怎麼講,才會更適當?
我覺得 (L變換) –> (處理) –> (L逆變換) 整個過程,
真的很像線性變換,把一個問題拿到另一個地方,變得很容易處理,處理完,再拿回原來的地方,比起在原地處理,輕鬆許多,這顯出「變換」帶來的優點。
另外,老師回答提到的逆變換:
在ds左方的exp(et),是不是exp(st)才對?
‘inf’是’\int’嗎?
抱歉,Latex的語法我不熟。
(1) L變換將問題由原來的時間函數空間的物件
(2) 我的確打錯了兩個地方,應該是
非齊次的常微分方程式最後找出來的特解(就由老師本文說講的)
請問特解是不是只有一個呢(唯一),還是有很多個呢?
這跟微分方程介紹「解的存在性和唯一性的想法」一樣嗎?
如果是只有一個,那 y" + 3y’ + 2y = 2
y = ( c1 e^-t + c2 e^-2t ) + 1
怎麼看就那個"1″是唯一的特解,零空間的反倒是無限多
那這又該如何解釋呢?微分方程和線性代數的特解形式,是有差別的嗎?
程度很差問了愚蠢的問題,希望老師可以指點迷津,再次謝謝周老師!
特解的名稱很容易使人混淆,前兩天也有同學問我這個問題。所謂的特解(particular solution)其實就是"任何一個解",而不是指某個很特別的解。齊次方程式
對於非齊次方程
這個結果可以如此解讀:
(1) 齊次方程的解基為
(2) 非齊次方程的特解有無窮多個,例如,
你說的唯一特解
所以我可以說:
非齊次方程不含零空間向量的那個解,yp = 1,是唯一的特解?
我在網路上看到一個網頁,好像是在講述抽象代數的
裡面有提到ring、group、field,好像也跟線性代數有關係?
其中:
http://math.ntnu.edu.tw/~li/algebra-html/node87.html
這裡面感覺很有趣且豐富,周老師的blog好像沒有類似的文章
如果用周老師簡潔明瞭的敘述方式,相信會更好懂、好玩的!
你提到的 ring(環), group(群), field(體)的抽象代數是數學系講授的內容,台灣在1960 年代採行"新數學"時期也曾經將這些主題放進高中數學,但在我進入中學前,這些內容又被移除了。過去我一直避開引用 field 一詞,而直接稱它為數域,即
其重要關鍵,我猜想,大概是自然指數函數吧!