维基百科,自由的百科全书
数学上,利萨茹(Lissajous)曲线(又称利萨茹图形、李萨如图形或鲍迪奇(Bowditch)曲线)是两个沿着互相垂直方向的正弦振动的合成的轨迹。
纳撒尼尔·鲍迪奇在1815年首先研究这一族曲线,朱尔·利萨茹在1857年作更详细研究。
 ,
, 。
。
 称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则
称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则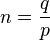 ,参数方程可以写作:
,参数方程可以写作:
 。
。
 ,
, ,
,  是奇数,
是奇数, 是偶数,
是偶数, 。
。
 , (6.1)
, (6.1)
 . (6.2)
. (6.2)
 ,
,  . (6.3)
. (6.3)
 , (6.2)
, (6.2)

 ,
,

 .
.
 . (6.4)
. (6.4)
 ,
,
 , (6. 5)
, (6. 5)
 ,
,
 . (6.6)
. (6.6)
 . (6.7)
. (6.7)
 ,
,
 .
.

 ,
,
 ,
,






 .
.

 ,
,
 ,
,
 . (6.9)
. (6.9)
 . (6.10)
. (6.10)
 ,
,
 .
.

 . (6.13)
. (6.13)

 ,
,
 ,
,
 ,
,
 ,
,
 和
和 


 , (6.14)
, (6.14)

 ,
,
 ,
,
 ,
,
 ,
,
 , (6.15)
, (6.15)
 (6.14)
(6.14)
 ,
,
 ,
,
 . (6.16)
. (6.16)
 ,
,
 , (6.17)
, (6.17)
 , (6.18)
, (6.18)
 . (6.19)
. (6.19)
 ,
,
 , (6.20)
, (6.20)
 . (6.21)
. (6.21)

纳撒尼尔·鲍迪奇在1815年首先研究这一族曲线,朱尔·利萨茹在1857年作更详细研究。
数学定义[编辑]
利萨茹曲线由以下参数方程定义: ,
, 。
。 称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则
称为曲线的参数,是两个正弦振动的频率比。若比例为有理数,则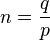 ,参数方程可以写作:
,参数方程可以写作: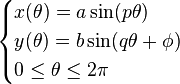 ,
,
 。
。性质[编辑]
- 若
 为偶数而
为偶数而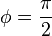 ,或若
,或若 为奇数而
为奇数而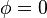 ,则曲线是第
,则曲线是第 个切比雪夫多项式
个切比雪夫多项式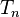 的曲线的一部份。
的曲线的一部份。
特别情况[编辑]
以下是利萨茹曲线的例子,其中 ,
, ,
,  是奇数,
是奇数, 是偶数,
是偶数, 。
。在電子學上的應用[编辑]
藉由使用利萨茹圖形可以測量出兩個信號的頻率比與相位差。§6.1 简谐振动
一 描述简谐振动的特征量
( 1 ) 简谐运动或简谐振动
若描述运动的变量x ( t ) (如物体的位移或角位移等)满足运动方程
则其解
所表示的振动,即用时间的正弦或余弦函数描述的振动。
( 2 ) 描述简谐振动的特征量
简谐振动可由振幅A、角频率w (或频率n、周期T )和相位j 这三个特征量完全确定下来。
振幅A :物体离开平衡位置的最大位移或角位移。
周期T :物体作一次完全振动所需的时间。
频率n :在单位时间内物体所作的完全振动的次数,它是周期的倒数。
角频率或圆频率w :频率n 的2p 倍。
相位j = :确定振动系统的瞬时运动状态。
:确定振动系统的瞬时运动状态。
特征量之间的关系式:
( 3 ) 描述简谐振动瞬时运动状态的特征量¾¾相位
简谐振动的振幅给出了振动的范围或幅度,简谐振动的角频率、频率或周期则给出了振动往复的快慢。
振幅和频率不能完全确定振动系统在任意瞬时的运动状态(位移、速度和加速度)。
简谐振动的位移、速度u 和加速度a:
当振幅A和角频率w 一定时,简谐振动的瞬时位移、速度和加速度都决定于量 ,这个量称为相位,用j表示,即
,这个量称为相位,用j表示,即
相位表示简谐振动在一个周期内所处的瞬时运动状态,单位是rad (弧度)。
当t = 0时,物体的初始位移和速度分别为:
式中j = j0称为初相位。由上式可解得:
相位的相对性:
对于单个简谐振动来说,我们总可以选择适当的计时零点,使初相位 为零;对于多个简谐振动来说,它们之间的相位差Dj 则起了重要的作用。
为零;对于多个简谐振动来说,它们之间的相位差Dj 则起了重要的作用。
两个同频率的简谐振动在同一时刻的相位差,恒等于它们的初相位之差,即当 时,有
时,有
相位差Dj有以下几种情况 :
:
1 )  ,两振动步调一致,同相位。
,两振动步调一致,同相位。
2 )  ,两振动步调相反,反相位。
,两振动步调相反,反相位。
3 ) 
 ,
, 超前
超前 ,
, 振动步调领先。
振动步调领先。
4 ) 
 ,
, 落后
落后 ,
, 振动步调落后。
振动步调落后。
5 )  ,可先把
,可先把 减去或加上2p的整数倍,然后再按上述方法确定相位的超前或落后。
减去或加上2p的整数倍,然后再按上述方法确定相位的超前或落后。
实际上,“x2比x1领先Dj”与“x2比x1落后(2p-Dj )”这两种说法是等价的。
二 简谐振动的合成
( 1 ) 同方向、同频率简谐振动的合成
质点同时参与了两个同方向、同频率的简谐振动,即
三角函数法:该质点的合振动为
即  , (6.8)
, (6.8)
其中  ,
,
即合成为与分振动同频率的简谐振动。
矢量图解法:简谐量对应于旋转矢量在x轴上的投影。同频简谐量的叠加,可看成是与它们对应的旋转矢量的合矢量在x轴上的投影。

图6 - 1 旋转矢量图


6 - 2 简谐振动的合成 图6 - 3 简谐振动的合成
(矢量图解法) (复数法)
复数法:简谐量对应于复数的实部,同频简谐量的叠加对应于相应复数叠加后所得到的合成复数的实部,即
注意:
① 同频简谐振动的合成,只需应用初相位。
② 简谐量本身所对应的是旋转矢量在x轴上的投影以及复数的实部。但是,在考虑简谐量的叠加时,却必须采用矢量合成以及复数加法。因为矢量和复数都分别有两个变量,即A和j,只有完整地考虑到了这两个变量,它们与简谐量的运算法则才是一致的。
③ 相位差的重要作用,合振幅。
对于
 有:
有:
1 )  ,
, ,合振幅最大;
,合振幅最大;
2 )  ,
, ,合振幅最小;
,合振幅最小;
3 ) 在一般情况下, .
.
( 2 ) 同方向、不同频率简谐振动的合成

图6 - 4 拍的形成
质点同时参与了角频率分别为w1和w2的两个同方向的简谐振动。
简化假定:两个分振动的振幅相同。
时间零点的选择:两振动相位相同的时刻。
这两个简谐振动可分别写为:
它们的合振动为
利用三角函数和差化积公式,可将式(6.9)改写为
研究这类振动合成问题的一种方法是画出振动的位移-时间关系图。只有当分振动周期之比是整数比时,才能产生周期性的非简谐的合振动。
拍(“准简谐振动”):当 时,可近似地将合振动看成是振幅
时,可近似地将合振动看成是振幅 缓慢变化的、角频率为
缓慢变化的、角频率为 的“准简谐振动”。频率都较大但两者相差很小的两个同方向简谐振动,合成时所产生的这种合振幅时而加强时而减弱的现象,称为拍。
的“准简谐振动”。频率都较大但两者相差很小的两个同方向简谐振动,合成时所产生的这种合振幅时而加强时而减弱的现象,称为拍。
拍频:这种合成振动的高频成分受到了低频调制,其包络的周期为 的周期的一半,即拍的周期和拍频分别为:
的周期的一半,即拍的周期和拍频分别为:
 ,
,
( 3 ) 垂直方向、同频率简谐振动的合成
设一质点同时参与了两个振动方向相互垂直的同频简谐振动,即
和  .
.
将式中的t消去,可得合振动的轨迹方程为
如图6-5中的第一行图形所示,质点合振动轨迹的具体形状以及质点沿椭圆轨迹的运动方向都取决于相位差 :
:
当 时,质点沿顺时针方向运动;
时,质点沿顺时针方向运动;
当 或
或 时,质点沿逆时针方向运动。此外,当A1 = A2时,正椭圆退化为圆。
时,质点沿逆时针方向运动。此外,当A1 = A2时,正椭圆退化为圆。
( 4 ) 垂直方向、不同频率简谐振动的合成
两个振动方向互相垂直的不同频率的简谐振动,合成后的运动一般来说比较复杂,而且其轨迹往往是不稳定的。

图6 - 5 垂直方向简谐振动的合成 李萨如图
如果两个简谐振动的频率之比 恰好是简单的整数比,则它们的合成运动具有稳定而闭合的轨迹,这些轨迹图形称为李萨如图。
恰好是简单的整数比,则它们的合成运动具有稳定而闭合的轨迹,这些轨迹图形称为李萨如图。
在图6 - 5所给出的图形中,选取了
其中m和n互为质数,p为正整数或零。这些图形是由两个垂直振动
合成的,它们的具体形状取决于比值 和相位差
和相位差 . 因此,可以在示波器上利用李萨如图来精确地比较频率。在数字频率计未被广泛采用之前,这是测量电信号频率的一种常用的简便方法。
. 因此,可以在示波器上利用李萨如图来精确地比较频率。在数字频率计未被广泛采用之前,这是测量电信号频率的一种常用的简便方法。
当两个振动方向相互垂直的简谐振动的频率之比是无理数时,合成的运动将永远不会重复已走过的路径,它的轨迹将逐渐密布在由振幅所限定的矩形面积内。这种非周期运动叫做准周期运动。拓扑学家证明了,准周期运动在结构上是不稳定的,参量稍有变化,例如引入微弱的耦合,构成它的两个振动的频率就会被锁定到一个相近的有理数比值上,这是一种同步锁模现象。

图6 - 6 准周期运动
三 振动的分解 傅里叶变换
( 1 ) 周期函数的频谱分析与傅里叶级数
一般情况下,振动的物理量可以具有比余弦函数复杂得多的形式。
1 ) 傅里叶定理:任一周期性函数 都可以表示为简谐函数的合成,即
都可以表示为简谐函数的合成,即
称为关于周期函数 的傅里叶级数,
的傅里叶级数, ,
, ,
, 和
和 ,
, 等称为傅里叶系数。
等称为傅里叶系数。
2 ) 正交函数系
在三角函数系
中,任意两个不同函数的乘积在区间 上的积分为零,即
上的积分为零,即
其中m和n是正整数,最后两式还要求 . 这就是说,三角函数系具有正交性,而傅里叶级数[式(6.14)]就是周期函数在正交的三角函数系中的展开式。
. 这就是说,三角函数系具有正交性,而傅里叶级数[式(6.14)]就是周期函数在正交的三角函数系中的展开式。
实际上,把任意函数分解成一组正交函数(不一定是三角函数系)的这种可能性,乃是理论物理和工程技术领域中最为重要和广泛应用的方法之一。
3 ) 傅里叶系数
由式(6.15)的正交关系以及式
可得, 的傅里叶系数分别为:
的傅里叶系数分别为:
4 ) 傅里叶级数的复数形式
利用欧拉公式(由复平面图可见, ,可导出欧拉公式):
,可导出欧拉公式):
我们还可以得到复数形式的傅里叶级数及其系数,它们分别为:
5 ) 频谱分析
利用傅里叶级数,任一复杂的周期性振动都可以分解为许多简谐振动,它们的频率为原周期性振动频率的整数倍。
在傅里叶级数中,k = 1的简谐振动与原周期性振动有相同的频率,称为基频振动;k = 2, 3 诸简谐振动称为k次谐频振动,通常还把这些振荡称为k次谐波。
诸简谐振动称为k次谐频振动,通常还把这些振荡称为k次谐波。
以这些简谐振动的频率为横坐标,以相应的振幅为纵坐标所作的图解,称为该振动的频谱。
周期性振动具有离散谱。这种将任一振动分解为许多简谐振动的方法,称为频谱分析。我们掌握了信号的内部结构¾¾“直流成分”及各次谐频,从而掌握了它在频率域上的图象,这往往比信号的波形还有用。
6 ) 分频
在利用傅里叶级数对周期性振动分解时,谐频都是基频的整数倍。然而,在另外
一些现象中,还会出现分数基频(如 ,
,
 )的谐频,通常称为次谐频。
)的谐频,通常称为次谐频。
1831年,法拉第曾观察到,当一个浅容器以频率n 在铅垂方向振荡时,其中的水会以n / 2的频率振荡。
1981年,人们用现代化手段重复了法拉第的实验,得到的不仅是1/2分频,还有1/4,1/12,1/14,1/16等一系列分频。这是一种非线性效应,但只有当非线性达到一定的程度时,才能激发起分数频率的次谐波。
分数频率意味着周期倍化,因此也称这种现象为倍周期分岔。这些现象预示着当前非线性科学的热点¾¾混沌现象的到来。
( 2 ) 非周期函数的频谱分析与傅里叶变换
非周期性的振动(如单个脉冲),可它展开为积分
或写成更普遍而对称的形式:
式(6.20)称为非周期函数 的傅里叶变换,而式(6.21)称为非周期函数
的傅里叶变换,而式(6.21)称为非周期函数 傅里叶积分。如图6-7(d)所示,非周期性振动的频谱是连续谱。
傅里叶积分。如图6-7(d)所示,非周期性振动的频谱是连续谱。

图6 - 7 离散谱和连续谱


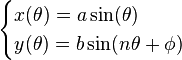
![[-a,a]\times[-b,b]](http://upload.wikimedia.org/math/f/d/f/fdf52692b1ab0250dcbfe3ec7ee70ca1.png) 中
中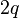 次
次![\phi \in \left(0,\frac{\pi}{2p} \right]](http://upload.wikimedia.org/math/6/3/4/634426a2c1ddf779280148ef9d654850.png) 对奇数
对奇数 对偶数
对偶数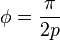 对偶数
对偶数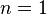 ,则曲线是
,则曲线是 (所以
(所以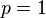 ),则曲线是
),则曲线是





No comments:
Post a Comment