http://blog.sina.com.cn/s/blog_a131787b0101dum8.html
統計力學- DemolabWiKi
www.phy.ntnu.edu.tw/wiki/index.php/統計力學
一起来学统计力学之第一篇
0.概述
统计力学的基本任务:
通过对微观状态及微观结构的研究来计算、预言宏观性质。
1.系综
一言以蔽之:系综就是吉布斯用来计算力学平均量的一个工具,有了它就可以将对时间的平均转变为系综的平均。
2.简并度
如下图,通常不同的粒子可能处于不同的能级,而处于同一能级上还存在着不同的状态,该能级上可能的状态数就叫做该能级的简并度,通常用g表示,如下图中E3能级的简并度为4。值得注意的是,在计算状态数的时候注意所研究的对象是费米子还是玻色子,费米子必须满足泡利不相容原理,而玻色子可以位于同一量子态。
3.状态数
宏观状态的确定只要求规定每一个能级上有多少个粒子,而不关心是哪些粒子。如果说有n1个粒子处于第一个能级的g1个量子态,n2个粒子处于第二个能级的g2个量子态上,那么可以用一系列数{ni}={n1,n2,n3,...,ni,....}来表示一个宏观状态,数列{ni}有时叫做一种分布。该种分布对应的微观状态数也就是一个宏观状态对应的微观状态数。家丁各种微观状态出现的几率是相同的,那么一种宏观状态下对一个的微观状态的数目越多,这种宏观转改出现的机会就越大。通常,人们称一个宏观状态对应的微观状态数目为这个宏观状态的热力学几率,这同数学上的几率有点区别,通常记作W。
4.等几率假设
在统计力学中我们通常假设体系处于任何一个微观态的几率是相等的;有了这个假设,我们一旦可以计算各种宏观状态所对应的微观状态数目,就可以找出几率最大的对应的宏观状态,即最可及状态,通常也是我们在试验中观察到的状态,这样我们就建立了从微观到宏观状态的联系。
5.计算状态数的例子
另外还可以直接利用下面推导的公式计算热力学几率:
7.统计力学中常用公式[不断更新中]
先给出最重要的一个公式:【Stirling's approximation ,斯特林近似公式】

或者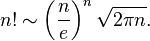
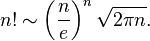
【Ref.】
李如生
刘光恒等
No comments:
Post a Comment