The Equivalence of Logistic Regression and Maximum Entropy Modeling
http://web.engr.illinois.edu/~mqian2/upload/research/notes/The%20Equivalence%20of%20Logistic%20Regression%20and%20Maximum%20Entropy%20Modeling.pdf
B. Dual Problem The dual problem of maximum entropy modeling is an unconstrained optimization problem
The Equivalence of Logistic Regression and Maximum Entropy
Modeling
Posterior probability
From Wikipedia, the free encyclopedia
| This article includes a list of references, but its sources remain unclear because it has insufficient inline citations. (November 2009) |
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence or background is taken into account. Similarly, the posterior probability distribution is the probability distribution of an unknown quantity, treated as a random variable,conditional on the evidence obtained from an experiment or survey. "Posterior", in this context, means after taking into account the relevant evidence related to the particular case being examined.
Definition[edit]
The posterior probability is the probability of the parameters  given the evidence
given the evidence  :
:  .
.
 given the evidence
given the evidence  :
:  .
.
It contrasts with the likelihood function, which is the probability of the evidence given the parameters:  .
.
 .
.
The two are related as follows:
Let us have a prior belief that the probability distribution function is 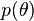 and observations
and observations  with the likelihood
with the likelihood 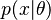 , then the posterior probability is defined as
, then the posterior probability is defined as
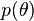 and observations
and observations  with the likelihood
with the likelihood 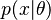 , then the posterior probability is defined as
, then the posterior probability is defined as
The posterior probability can be written in the memorable form as


No comments:
Post a Comment