Two-Stage sampling in SAS/IML software http://blogs.sas.com/content/iml/2015/05/13/sampling-hierarchical-data.html

SAS BLOGS HOME > THE DO LOOP > TWO-STAGE SAMPLING OF HIERARCHICAL DATA IN SAS

Two-stage sampling of hierarchical data in SAS

Rick Wicklin|MAY 13, 2015

• 2703
• 0
• inShare1

I always learn something new when I attend SAS Global Forum, and it often results from an informal conversations in The Quad or in a hallway. Last week a SAS customer described a scenario that he wanted to implement as part of an analysis of some genetic data. To oversimplify the problem, his data contained nested categorical variables. He wanted to randomly sample several values from the outer variable and then randomly sample values of the inner variable from within the selected levels of the outer variable.

I don't know much about genetics, but this kind of sampling is used in survey sampling. For example, a researcher can randomly select states and then randomly select counties within those states. Or a researcher can randomly select schools and teachers within those schools to assess classroom performance. In each case, the data are hierarchical because of the nested variables.

The customer suspected that he could use PROC SURVEYSELECT for this sampling scenario, but neither of us had experience with this sampling scheme. However, an email exchange with a SAS colleague provided the details. I saw the customer again at the Kickback Party on the last night of SAS Global Forum. While the band played in the ballroom, we found a quiet hallway and I described how to use the SURVEYSELECT procedure to select a random sample for this kind of nested data.

Two-stage sampling by using PROC SURVEYSELECT

The trick is to call the SURVEYSELECT procedure twice. I will illustrate the technique by using the SasHelp.Zipcode data, which contains counties (the inner variable) that are nested within states (the outer variable). For this example, the task will be to randomly select three states, then to randomly select two counties for each of the selected states.

The following call to PROC SURVEYSELECT randomly selects three states:

proc surveyselect data=sashelp.Zipcode noprint sampsize=3 seed=54321 out=ClusterSample; cluster State; /* or use PPS option for nonuniform probability */ run;   proc freq data=ClusterSample; tables StateName / nocum nopercent; run;

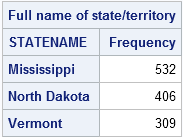
The SURVEYSELECT procedure creates an output data set named ClusterSample that contains 1,247 observations. Each observation corresponds to a zip code. The output from PROC FREQ shows that the selected states were Mississippi (which contains 532 zip codes), North Dakota (which contains 406 zip codes), and Vermont (which contains 309 zip codes). By using the CLUSTER statement, the procedure outputs allobservations for each selected state.

This output data set becomes the input data set for a second call to PROC SURVEYSELECT. In the second call, you can use the STRATA statement to specify that you want to select from within each of the three states. You can use the CLUSTER statement yet again to extract all observations for a random sample of two counties from each state:

proc surveyselect data=ClusterSample noprint sampsize=2 seed=65432 out=StrataSample; strata State; cluster County; run;     proc freq data=StrataSample; tables StateName*CountyNM / list nocum nopct norow nocol; run;

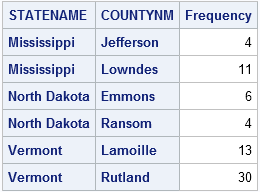
You can see that the procedure selected Jefferson and Lowndes counties for Mississippi. There are 15 zip codes in those two counties. For North Dakota, Emmons and Ransom counties were selected, which contain 10 zip codes. For Vermont, Lamoille and Rutland counties were selected, which contain 43 zip codes.

You can use all of the usual SURVEYSELECT options to produce multiple samples (REPS= option) or to change the method for sample selection (METHOD= option). Details are provided in the documentation for the SURVEYSELECT procedure.

Two-Stage sampling in SAS/IML software

The SURVEYSELECT procedure is the best choice for implementing this hierarchical sampling scheme. However, it is an interesting programming exercise to implement this two-stage sampling in the SAS/IML language. You can use the SAMPLE function to sample without replacement, and combine that technique withthe LOC-ELEMENT trick. As explained in my previous post, the following statements generate the row numbers for a random selection of three states. The row numbers are then used to form a new matrix that contains only the selected states. This matrix is analogous to the output that is produced by the first call to PROC SURVEYSELECT.

proc iml; use sashelp.Zipcode; read all var _NUM_ into X[colname=nVarNames]; read all var _CHAR_ into C[colname=cVarNames]; close sashelp.Zipcode;   call randseed(54321); uState = unique(X[, "State"]); /* state numbers in sorted order */ SampState = sample(uState, 3, "NoReplace"); /* choose 3 states at random */ ClusterIdx = loc(element(X[, "State"],SampState)); /* row numbers for states */   /* form ClusterSample = subset of selected states */ X = X[ClusterIdx,]; mattrib X colname=nVarNames; C = C[ClusterIdx,]; mattrib C colname=cVarNames;

For the next stage of sampling, you can use a DO loop to iterate over the states. For each state, the following statements randomly select two counties. The LOC-ELEMENT trick is used to generate the row numbers, and a concatenation operator is used to accumulate the row numbers for the six selected counties:

/* for each selected state, select 2 counties */ free SelIdx; do i = 1 to ncol(SampState); stateIdx = loc(X[, "State"] = SampState[i]); /* get obs for i_th state */ uCounty = unique(X[stateIdx, "County"]); /* all counties for state */ SampCounty = sample(uCounty, 2, "NoReplace"); /* choose 2 counties at random */ countyIdx = loc(element(X[, "County"],SampCounty)); /* row numbers for counties */ SelIdx = SelIdx || xsect(stateIdx, countyIdx); end;   v = {"StateName" "CountyNM"}; results = trim(C[selIdx, v]) || putn(X[SelIdx,"Zip"], "Z5."); print results[c=(v||"Zip")];

The experienced programmer will notice that concatenating vectors inside a loop is not optimally efficient. I didn't want to over-complicate this program by worrying about efficiency, so I will leave it to the motivated reader to rewrite the program without using concatenation. The REMOVE function might be useful for this task.

In summary, you can perform cluster sampling of hierarchical data by calling the SURVEYSELECT procedure twice. If you need to perform cluster sampling for data that are in a SAS/IML matrix, PROC IML provides the SAMPLE function and the LOC-ELEMENT trick, which enable you to write your own algorithm to extract random samples from nested data.