| 3. 拓樸熵 (Topological Entropy) |
連續性是自然界的基本屬性之一。數學上連續的概念是由拓樸來刻劃的。 拓樸空間
X 中由所有開集生成的 Borel 代數相當於測度空間裡的
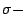
代數。 拓樸空間上的連續映射相當於測度空間裡的可測變換。 由此,我們可以將上節中所談的 Kolmogorov 熵在拓樸空間裡做相似性的定義, 來描述連續映射的不確定性。在這過程中最大的困擾是: 一般拓樸空間中,並沒有一個相似於測度空間裡的「測度」的度量。
假設
X 為一個緊緻 (compact) Hausdorff 空間,
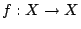
為一連續映射。由一般拓樸學知,存在有限開覆蓋 (finite open covering)。 設
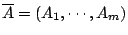
,為
X 的一個有限開覆蓋,

中能覆蓋
X 的子集族稱為

中的子覆蓋 (subcover)。 我們稱

中的子覆蓋為「極小」(minimal),如果在

中沒有一個比它元素少的子覆蓋。 通常用
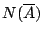
來代表

中極小子覆蓋裡元素的個數。 若把極小子覆蓋裡的每一個開集當做一個「基本事件」,大家的概率都是
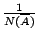
,我們則得到一個樣本空間。它的 Shannon 熵可以很輕易的算出,是
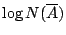
。我們稱這個數目為開覆蓋

的熵,同時用符號 H(A) 來表示。
當

為
X 上的開覆蓋時,
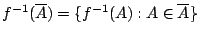
也是一個開覆蓋。 若
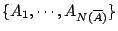
是
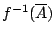
的一個子覆蓋,但不一定是極小。所以,
若 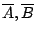 為 X 上的二個開覆蓋, 則
為 X 上的二個開覆蓋, 則 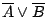 代表
代表 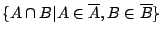 這個開覆蓋。若
這個開覆蓋。若 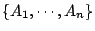 是一個
是一個  的子覆蓋
的子覆蓋 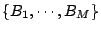 是
是 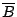 的一個子覆蓋, 則
的一個子覆蓋, 則 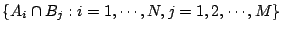 是
是 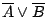 的一個子覆蓋。 因此,
的一個子覆蓋。 因此, 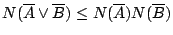 以及
我們還是用
以及
我們還是用 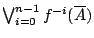 來代表
來代表 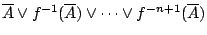 , 同時用
, 同時用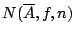 來表示覆蓋
來表示覆蓋 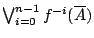 中的極小子覆蓋元素的個數。相似於定義 2-2',我們定義:
中的極小子覆蓋元素的個數。相似於定義 2-2',我們定義:
- 定義3-1:
- 連續映射 f 關於有限覆蓋
 的拓樸熵 (topolgical entropy) 定義為:
的拓樸熵 (topolgical entropy) 定義為:
- 定義3-2:
- 緊緻 Hausdorff 拓樸空間 X 上的連續映射 f 的拓樸熵為
要使上述關於拓樸熵的定義合理,我們必須證明定義3-1中的極限的存在。 為此我們求助於下列仍然是初等微積分的結果。
- 引理3-3:
- 設實數序列
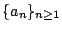 滿足條件
滿足條件 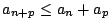 ,
, 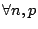 , 則
, 則 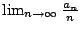 存在且等於
存在且等於 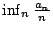 。
。
- 證明:
- 固定p > 0,每個n>0可寫成n=kp+i,其中
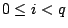 ,則
,則
當 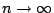 時
時 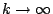 ,故有
,故有
因此, 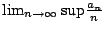
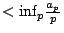 另一方面,從不等式
另一方面,從不等式
可知,極限 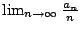 存在且等於
存在且等於 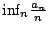 可知,極限
可知,極限 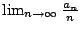 存在且等於
存在且等於 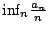
- 定理3-4:
- 設 X 為緊緻 Hausdorff 空間,
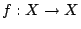 連續。任給 X 的有限開覆蓋
連續。任給 X 的有限開覆蓋  ,極限
,極限
- 證明:
- 由定義知,
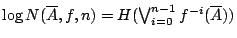 , 我們令其為 an。由(3-1),(3-2)可知
, 我們令其為 an。由(3-1),(3-2)可知
定理由結論恰由引理3-3推導。
拓樸嫡是由 R. Adler, A. Konhein 及 M. McAndrew 在1965年引進的, 它是為了研究關於拓樸共軛不變量應運而生的。 拓樸共軛的定義可如下給出。
- 定義3-5:
- 設
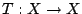 和
和 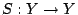 分別為緊緻拓樸空間 X 和 Y 上的連續映射。 若存在同胚 (homeomorphism)
分別為緊緻拓樸空間 X 和 Y 上的連續映射。 若存在同胚 (homeomorphism) 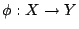 使得
使得 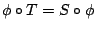 , 則稱拓樸共軛 (topologically conjugate) 於 S。 這時,
, 則稱拓樸共軛 (topologically conjugate) 於 S。 這時,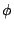 就稱為一個共軛。
就稱為一個共軛。
我們可以證明,拓樸熵是拓樸共軛性的一個不變量。也就是說,兩個拓樸共軛的連續映射有相同的拓樸熵,反之亦然。事實上兩個拓樸共軛的連續映射在本質上給出相同的遍歷性質,因此,拓樸熵數學地刻劃了不同共軛類的拓樸動力系統 (Topological dynamical system) 的性質。
我們已知拓樸空間
X 加上其全體開集張成的 Borel
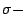
代數 β 構成一個可測空間。
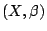
,而 β 上給定的任何一個概率測度 μ 就構成一個概率測度空間
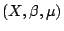
。
X 上的任一連續映射
f 同時也為
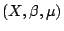
上的可測變換,因而就有一個 Kolmogorov 熵隨之確定。 另一方面,Borel 代數 β 上存在著眾多不同的概率測度,這樣就有了對應於不同概率測度的 Kolmogorov 熵組成的數集。 然而,作為連續映射
f 的拓樸熵之定義與測度無關,它是唯一確定的。我們自然發出疑問:這兩種熵有何內在聯繫? 既然拓樸嫡概念是由 Kolmogorov 熵概念衍生而來,我們有信心認為它們的確存在著情同手足的關係。 這方面的結果多采多姿。比如說,
- 定理3-8:
- 設 f 為緊緻拓樸空間 X 上的連續映射,則
本節拓樸熵中,空間為緊緻的假設並非必要。 70年代初 Dinaburg 和 Bowen 分別給出了拓樸熵的等價定義。 這些定義的優越性在於它們引導了一系列關於拓樸熵和測度熵(Kolmogorov 熵) 之間聯繫結果的證明。Bowen 的定義是對更廣泛的距離空間上一致連續映射族而言的。 且導致了
n-環面上自同構拓樸熵公式的幾何證明。 可惜,這位在遍歷理論研究中做出突出成就的數學家剛過而立之年就與世長辭了
 的拓樸熵 (topolgical entropy) 定義為:
的拓樸熵 (topolgical entropy) 定義為: 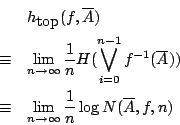
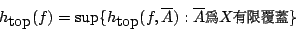
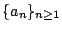 滿足條件
滿足條件 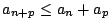 ,
, 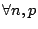 , 則
, 則 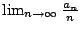 存在且等於
存在且等於 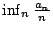 。
。 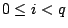 ,則
,則 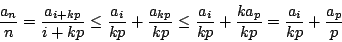 當
當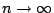 時
時 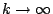 ,故有
,故有 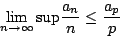 因此,
因此,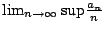
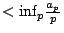 另一方面,從不等式
另一方面,從不等式 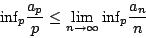 可知,極限
可知,極限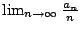 存在且等於
存在且等於 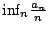 可知,極限
可知,極限 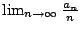 存在且等於
存在且等於 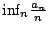
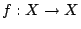 連續。任給 X 的有限開覆蓋
連續。任給 X 的有限開覆蓋  ,極限
,極限 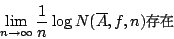
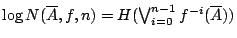 , 我們令其為 an。由(3-1),(3-2)可知
, 我們令其為 an。由(3-1),(3-2)可知 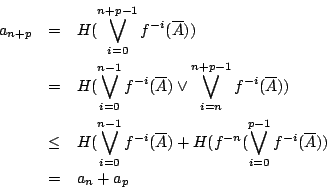
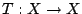 和
和 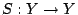 分別為緊緻拓樸空間 X 和 Y 上的連續映射。 若存在同胚 (homeomorphism)
分別為緊緻拓樸空間 X 和 Y 上的連續映射。 若存在同胚 (homeomorphism) 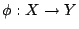 使得
使得 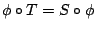 , 則稱拓樸共軛 (topologically conjugate) 於 S。 這時,
, 則稱拓樸共軛 (topologically conjugate) 於 S。 這時,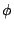 就稱為一個共軛。
就稱為一個共軛。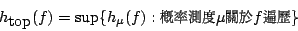
No comments:
Post a Comment