什么是熵-------第四部分
| 4. Boltzmann 熵 |
設
的非負函數了 f(x) 稱為密度函數,其集合記為 D。 易見等式
定義了
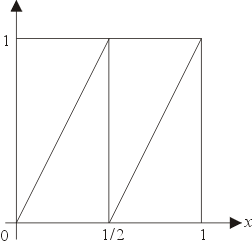 圖4-1 |
- 定義4-1:
- 設
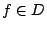 且
且 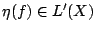 則 f 的 Boltzamann 熵定義為
則 f 的 Boltzamann 熵定義為 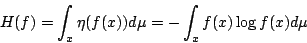
| = | 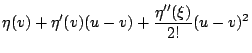 | (1) | |
| < | (2) |
即,
簡化之,我們便有有名的 Gibbs 不等式,
任給函數
由於
在有限的樣本空間 (X,p1,…,pn) 中,Shannon 熵在 p1=p2= … =pn=n 時為最大,Boltzmann 熵在概率測度空間裡也有類似的性質。
- 命題4-2:
- 設
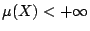 ,則密度函數
,則密度函數 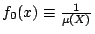 滿足
滿足 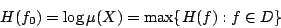
- 證明:
- 首先易見
 。其次,任給
。其次,任給 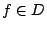 ,由不等式(4-1)
,由不等式(4-1) 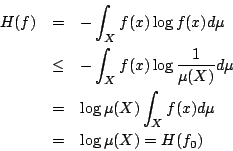
稱為 X 的期望值 (Expected Value 或 Expectation)。 而數
則稱為 X 的變異數 (variance)。期望值是關於於隨機變量 X 平均值的一個度量, 變異數則表示隨機變量偏離其平均值的程度。下列性質,可以輕易的被驗證:
- (i)
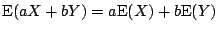
- (ii)
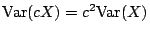
- (iii)
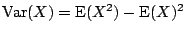
- (iv) 若 X 和 Y「獨立(independent)」則
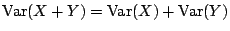
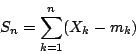
則,
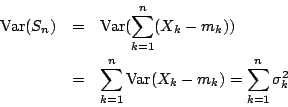
我們標準化 Sn,即令
則
其中 P 為樣本空間的概率分佈。 但是,為什麼大家都遵循的是 Gauss 分佈規律,而不是其他的分佈規律呢?事實上, 這和熱力學第二定律有異曲同工之妙。熱力學第二定律大致上說,自然界的規律是,一切動態系統都是在向「熵」高的方向發展。 從這個角度來看,在
記
- 命題4-3
- 設
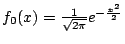 ,則
,則 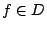 且
且 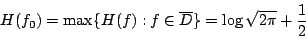
- 證明:
- 由公式
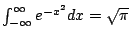 ,易知
,易知 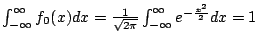 即
即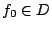 ,又由部分積分法易證
,又由部分積分法易證 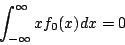 以及
以及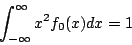 則
則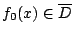 ,由不等式(4-1)
,由不等式(4-1) ![\begin{eqnarray*}H(f) &= & \int_{-\infty}^{\infty} f(x) \log{f(x)}dx\\&\leq&......sqrt{2\pi}} ]dx \\&=& \log{(\sqrt{2\pi})}+\frac{1}{2} = H(f_0)\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/img274.gif)
- 命題4-4:
- 設
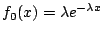 ,則
,則 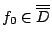 , 且
, 且 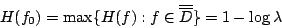
則H(f)在此約束下,最大值的密度函數應為
其中r為一常數。同樣,若有兩個約束
和
則密度函數
給出了H(f)在這兩個約束下的最大值H(f0), 其中r1,r2為兩常數。更一般地,我們有
- 命題4-4:
- 設
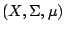 為一測度空間,非負函數
為一測度空間,非負函數 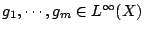 及正常數 r1,…,rm 滿足條件
及正常數 r1,…,rm 滿足條件 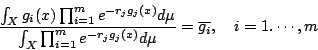 則 H(f) 在約束
則 H(f) 在約束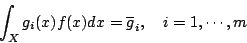 下最大密度值函數為
下最大密度值函數為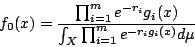
- 證明:
- 為簡單起見,令
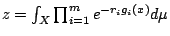 ,則
,則 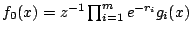 。 不難算出
。 不難算出 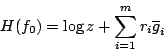 任給密度函數 f 滿足上述約束條件,由不等式(4-1)知,
任給密度函數 f 滿足上述約束條件,由不等式(4-1)知,![\begin{eqnarray*}H(f)&\leq& -\int_X f(x) \log{[z^{-1} \prod_{i=1}^{m} e^{-r_ig......] d\mu \\&=& \log{z} + \sum_{i=1}^{m} r_i\overline{g}_i=H(f_0)\end{eqnarray*}](http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/img292.gif)
转载自:http://episte.math.ntu.edu.tw/articles/mm/mm_13_3_01/index.html
No comments:
Post a Comment