博文
次序中的物理学 
精选
|||
数学中有许多计算上的前后次序问题，不同的次序甚至不同的处理方法给出的结果不同。要用一个可控的规则给出一个可以接受的结果，就产生了积分主值，级数主值，函数主值等概念。
物理中也有许多计算上的前后次序问题，不同的次序的物理结果可能不同。孰是孰非? 尽管有些规则可援，很多问题却不能从物理原则方面给出判断。最有名的例子就是量子场论中的重整化规则，李政道和杨振宁还给出过一个统计物理的例子。
一、数学中的次序一例
学习理论物理，绕不过如下积分(缩写形式)
(1) 
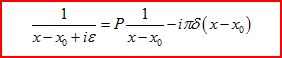
用狄拉克的说法(取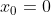
)(Principles，P.61，Eq.(15))
(2) 
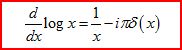
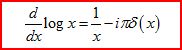
这个式子，表示在实轴上对1/x进行积分时，应当取主值部分。细究这个问题，会发现有一个次序的不可颠倒性。
考虑复平面上的熟知的回路积分
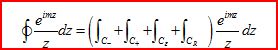
当m取正实数，根据约当引理，回路积分等式右边的第四项积分(实轴上以原点为圆心的大半圆)为零；而m --> 0+时，等式右边的第一、二项为在实轴上对1/x积分的主值；第三项积分结果为 i pi；再由残数定理，方程左边积分值为零。故得：
(3) 
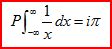
这个积分中，不只有一个先后次序。但这里只讨论其中大家不太注意的如下次序问题。
次序一：先取m有限，给出积分，然后让m --> 0+，有积分结果(3)。
次序二：先让m --> 0+，约当引理用不上，得不出结果(3)。
如果没有物理实验的支持，不知道数学本身能否判断这两个次序哪一个正确? 而物理实验的结果，举凡来自量子力学、量子场论、凝聚态物理、统计物理等等，都支持次序一，无一例外。
二、李政道和杨振宁给出的例子：物理中有次序
范德瓦尔气体状态方程比理想气体高明的地方在于它可以初步描述相变，而真实的情况就复杂很多。考虑一个量子非理想气体，从高温往低温降温，必定会经历相变。在统计物理中，先把配方函数写出来，就可写出物态方程。在数学上，物态方程由一个无穷级数表示，而这个级数的每个项的系数都是体积V的函数。下面有两个次序：
次序一，先把无穷级数求出来，再让V取无限。
次序二，先取V为无限，再求无穷级数。
李政道和杨振宁发现，只有次序一才是合理的。而次序二，历史上被很多巨擘使用过(例迈耶、玻恩、乌伦贝克等)，李杨认为他们从“猜想到‘证明’都是错误的”。
就这个问题，李政道提出如下猜想：先让体积V有限，研究无穷级数的性质然后让V取无限，“这是合乎物理实际的”(统计力学，P.113)。
三、推广的李杨猜想：次序中有物理
在理论物理中，如同时涉及纯数学极限和物理极限的计算，应该先完成数学处理，然后再取物理近似。不妨称之为推广的李杨猜想。
例子1：统计物理中这类问题很多，一般的规则应当是最后取热力学极限，因为热力学极限是物理极限。
例子2：时空问题麻烦一点。完全可以认为四维的时空就是时空的全部，无须假设更高维时空的存在。也完全可以假设四维的时空是嵌在更高维时空的一个超面，而四维以外的时空卷起来了。这两个理论是反映的是不同的宇宙观！是不同的宇宙理论。
例子3：近十来年，物理学界关注碳纳米管的如下问题。碳纳米管上载流子的输运、碳纳米管本身绕对称轴的旋转(参见：Physical Review B, 65(2002) 161401(R))等，存在如下次序问题：
次序一：碳纳米管是一个几何面，厚度为零。旋转是绕刚性轴进行的，建立量子力学。结果表明能量没有零点能。
次序二：几何面实际上是物理上有厚度的薄壳的极限，先有薄壳内的量子力学，然后让厚度为零。结果表明有零点能。
东京工业大学的尾上順教授小组，四月份报告了一个漂亮的实验结果，首次证明次序二是正确的!(Jun Onoe, et. al., Observation of Riemannian geometric effects on electronic states, EPL,98(2012)27001).
不要小看这个零点能。试看茫茫宇宙，暗能量还是一朵乌云哩。
http://blog.sciencenet.cn/blog-3377-579070.html
上一篇：物理学与“虚无”中诗性的创造
下一篇：杨振宁先生论物理创造的诗性体验
43 陈小润 刘进平 武夷山 沈惠川 李学宽 郭斌 李铭 李贵发 武京治 吕喆 李泳 程智 屈林 赵凯 李毅伟 杜敏彪 邸利会 文文 左正伟 葛素红 鲍得海 罗会仟 林涛 王国强 唐常杰 苏力宏 张晗 赵国求 黄秀清 张志东 许先进 侯吉旋 陆振烟 杨正瓴 刘俊明 ZeroK haoye jfeng95 paulings yunmu wuhuike qianxun1991gmai EurekaYah
该博文允许注册用户评论 请点击登录 评论 (28 个评论)
- [28]薛堪豪
- 多谢 !
- [27]薛堪豪
- 刘老师可否解释一下第一个公式，其中 \epsilon 取 0+ 或者 0-, 怎么会出现一个 pi 来的呢？
我以前做非平衡格林函数的时候遇到了这个东西，但不知道怎么算的，虽然 delta 函数是比较明显，但为何出现 pi 的因子？ 可否指教，多谢！ - 博主回复(2012-11-13 15:28)：第一个公式其实是积分的简洁表示式。而这个积分，只能在复平面上进行，这样出现一个pi就很正常了。
- [26]欧阳峰
- 我不懂其中细节，但我觉得数学上对于次序应该有个“说法”。物理上在积分次序等事情上玩花样，应该是暗藏了数学上的不严密，“走捷径”的做法。
- [25]沈惠川
- 另：范洪义的IWOP技术中也用到了量子场论中的有序积分法。
博主回复(2012-8-2 08:07)：物理学具有其深刻性，次序交换也是其深刻性一面。
尽管对范先生的IWOP技术不熟悉，相信其中一定有一些次序问题。
.－－－－－－－－－－－－－－－－－－－－－－－－－－－
Possion括号实际上也是一种“次序”（有正负号）。 - 博主回复(2012-8-6 05:29)：我现在知道，在尘世中，凡属没有次序或者正常次序的地方都是平庸的；而凡属有反常次序的地方才都是非平庸的。
当人情碰到规则出现矛盾；
当科学性和群体可接受性出现矛盾；
当体育精神和心态出现矛盾；
......
- [24]沈惠川
- 当相对论要求与热力学要求出现在同一问题中时，总是首先满足相对论要求。
另：范洪义的IWOP技术中也用到了量子场论中的有序积分法。 - 博主回复(2012-8-2 08:07)：物理学具有其深刻性，次序交换也是其深刻性一面。
尽管对范先生的IWOP技术不熟悉，相信其中一定有一些次序问题。
- [23]刘俊明
- 赞同！物理的次序要求随处可见呢，例如经典电磁学中就有类似问题！
- 博主回复(2012-8-2 09:01)：这两天伦敦奥运正热，我方有两位羽毛球女子双打世界女双一号被逐出奥运村。
这里也有一个次序不可交换性：当奥林匹克精神和竞赛规则矛盾时，首先必须遵守当奥林匹克精神。
- [22]王国强
- 我查看了一下，发现零点能这个概念，最初是通过跟经典体系的最低能量的比较中来的，例如周世勋先生的《量子力学》p31，谐振子部份，说，
“有关光被晶体散射的实验证明了零点能的存在。光被晶体散射是由于晶体中原子的振动。按照经典理论，当温度趋向绝对零度时，原子（动）能量趋近于零，原子趋于静止，这是就不会引起光的散射。实验证明，温度趋向于绝对零度时，散射光的强度趋向某一不为零的极限值。这说明即使在绝对零度，原子仍有零点振动。“
然后，后面又用不确定关系说明了，线性谐振子的零点能的存在，是符合不确定关系式的 －－－ 从不确定关系式推导出了线性谐振子的最小能量恰好是其基态能量（零点能）。
所以，我认为，我们应该摆脱与经典概念的纠缠，直接指出，所谓的零点能，实质就是指一个定态量子系统的基态能量，而基态是必定存在的，即零点能也是必定存在的。
话说回来，刘老师的这句，”结果表明能量没有零点能。“ 到底具体指什么？ 没有妨碍的话，是否可以看看论文原文？ 如果有的话。
- [21]王国强
- 谢谢刘老师的指正，不确定性原理（Uncertainty principle），可能只是一种沿袭的称呼，而并非量子力学公理化体系中的基本原理。但是这似乎不影响讨论的实质，因为既然量子力学标准体系中存在一个不确定性定理，那么问题就转为了，这个不确定（关系）性定理是否是普遍适用的 －－ 即是否可以认为所有的量子系统都存在零点能呢？ 我想可能答案还是：
似乎不行。
^_^。。。。。。。。。 - 博主回复(2012-6-13 07:40)：这个问题，........。
如果着眼于每个量子系统，例如氢原子等等，答案是否定的。
但是，如果放眼于整个宇宙，还是一个辐射场，没有几个氢原子，就可以说零点能无处不在了。
- [20]陆振烟
- 很有趣，还有这样的意思，虽然这块知识我学得不精。（1）式子和举的杨李的例子在量子多体理论中常用到，看这篇博文后，发现多体理论中确实也是取次序二：先求和或积分，再取极限。我有个想法：或许以后碰到积分也应该按次序二来做（毕竟积分就代表求和），谢谢分享。
- 博主回复(2012-6-12 08:25)：如果积分有物理意义，当按次序二；如果没有物理意义，当循数学规则。
- [19]侯吉旋
- 记得您教我们热统的时候，我就问过一个问题，为什么实际气体的焦汤系数在压强趋于0的时候不像理想气体那样趋于0. 最后还是个运算次序问题。
- 博主回复(2012-6-12 08:26)：就是如此。
- [18]田灿荣
- 碳纳米管中的次序二先求极限，然后再将0代入。统计物理中次序一先求级数（其实就是极限），然后再将V代入。我从数学上理解，就是积分（或者级数）与极限的可交换性，并不是所有情况下积分与极限是可以交换的，仅仅积分满足控制收敛定理才可以交换。
- 博主回复(2012-6-12 08:27)：问题稍微复杂一点，这里会碰到不同积分次序结果不同的问题。
- [17]王国强
- 是呀，正是因为对 零点能的存在 的解释是用 不确定原理， 而据说 不确定原理 是普遍适用的，因此自然而然的可以认为，所有的量子系统都存在零点能。
自然也包括转子系统在内的任意系统。
这个结论是不是真的是普遍的呢？
即 零点能的存在归因于不确定原理，而不确定原理普遍成立，因此零点能普遍存在。
呢？ - 博主回复(2012-6-12 08:30)：似乎不行。
我是量子力学原理的信奉者，量子力学标准体系中没有不确定原理！只又不确定关系、或者不确定性定理。
在半经典理论中，有一个不确定性原理。
- [16]李毅伟
- 早先的做法可能出于简化的原因而忽略了部分真实性。在科学研究中，有时最初的做法会流行很久。
- 博主回复(2012-6-8 18:21)：对！这可能就是所谓的先机问题。
- [15]李毅伟
- 物理中的次序还是次序中的物理？
- 博主回复(2012-6-8 18:13)：先在物理中发现有次序，后在次序中思考物理。
- [14]hshnxyj
- 范德瓦尔斯气体与理想气体这个刘老师在小考试考过，当时我们都当做没有区别做了。后来才知道这
其中有着丰富的物理内涵。 - 博主回复(2012-6-8 18:13)：
- [13]田灿荣
- 貌似统计物理中的次序一、二与碳纳米管中的次序一、二，排序的标准是相反的。
- 博主回复(2012-6-8 18:14)：应该是一样的。
- [12]bangcheng
- 俺粗浅理解，楼主的秩序是空间范围，即确定边界条件的程序，如果不先确定适用范围而随意计算，就得不出结果
- [11]程智
- 这种顺序倒是容易解释的，因为必须先有模型，然后才有近似。如果先做近似，意味着就没有模型了，自然也就不可能获得逻辑上说得通的结果。就如同生物学中那样，先近似地认为“突变”是随机的，然后再由这个近似得出一些似是而非的结论，显然整套理论的完备性值得怀疑。
- 博主回复(2012-6-8 18:16)：科学研究本身就像探险。
- [10]sowhathen
- "如果没有物理实验的支持，不知道数学本身能否判断这两个次序哪一个正确?"
希望博主或者牛人能回答这个好问题，至少给点线索。 - 博主回复(2012-6-8 18:17)：实践是检验真理的唯一标准。
- [9]wuhuike
- 可不可以认为，这个“次序”，等效于“时间”？
- 博主回复(2012-6-8 18:18)：这个次序是手续上的先后，不似物理时间上的先后。
- [8]罗会仟
- 老刘真有心，这么仔细地敲公式，不懂量子场论的人只好飘过。
- 博主回复(2012-6-8 18:19)：其实我用了更多的时间在网页公式上，后来发现出来的是乱码，才用图片替代之。
- [7]谢柏松
- 好文，拜读！有限情况下的一个可能理解是abcd四边形，先ab再bc与先ad(与bc等效)再dc(与ab等效)的确可以产生不同的结果，例如矢量场曲面上的输运，李导数等。但涉及无限大和极限情况下的order问题的确不好理解。
- 博主回复(2012-6-8 18:20)：柏松兄笑话了。
不过，“涉及无限大和极限情况下的order问题的确不好理解”。
- [6]文文
- 什么事情都有次序！
- 博主回复(2012-6-8 18:24)：类空间隔发生的事件没有先后次序。
- [5]王国强
- 另外，不知道这个“零点能”，具体何指。
如果是指量子系统中“普遍存在”的那个零点能，例如量子“振子”的1/2 hw的话， 记得这个零点能的解释是认为起源于量子力学的不确定性原理 － 这也意味着 量子系统的零点能是普遍存在的，甚至是必定存在的 。
如果这样的话，那么就可以从零点能应该普遍存在这个结论上，自然得出，纳米管没有零点能的次序一，是不正确的。 - 博主回复(2012-6-8 18:25)：不要以为只有谐振动才会有零点能，转动也可能会出现。
- [4]王国强
- 术语里也有
时序 sequential
这个词呀。 - 博主回复(2012-6-8 18:25)：这个接近于物理的时序。
- [3]吕喆
- 不许“夹楔”！
- 博主回复(2012-6-8 18:23)：
- [2]mirrorliwei
- order的感觉只是个“序”。
顺+序感觉是在时间轴上的order，次+序感觉是在空间间上的order。主次、上下、前后等，是说“次序”，在一个时刻里分布。而“顺序”是有时间差的，讲究“先和后”。 - 博主回复(2012-6-6 08:29)：有理！ 容我再考虑。
- [1]mirrorliwei
- 也许用“顺序”比“次序”好些。
- 博主回复(2012-6-6 08:02)：想过！ 由于觉得似乎“顺序”比“次序”接近日常一点，故而未用。
英文就没有这个问题，一个order搞掂~！
1/1 | 总计:28 | 首页 | 上一页 | 下一页 | 末页 | 跳转
|
No comments:
Post a Comment