维基周边,你身边的维基百科!立刻关注“维基周边”微信公众账号,了解你周围的大千世界
| [关闭] |
拉普拉斯-龍格-冷次向量[编辑]
维基百科,自由的百科全书
氫原子是由兩個帶電粒子構成的。這兩個帶電粒子以遵守庫侖定律的靜電力互相作用.靜電力是一個標準的平方反比連心力。所以,氫原子內部的微觀運動是一個克卜勒問題。在量子力學的發展初期,薛丁格還在思索他的薛丁格方程式的時候,沃爾夫岡·包立使用 LRL 向量,關鍵性地推導出氫原子的發射光譜[3]。這結果給予物理學家很大的信心,量子力學理論是正確的。
在經典力學與量子力學裏,因為物理系統的某一種對稱性,會產生一個或多個對應的保守值。 LRL 向量也不例外。可是,它相對應的對稱性很特別;在數學裏,克卜勒問題等價於 一個粒子自由地移動於 四維空間的三維球面[4];所以,整個問題涉及四維空間的某種旋轉對稱[5]。
拉普拉斯-龍格-冷次向量是因皮埃爾-西蒙·拉普拉斯,卡爾·龍格,與威爾漢·冷次而命名。它又稱為拉普拉斯向量,龍格-冷次向量,或冷次向量。有趣的是,LRL 向量並不是這三位先生發現的!這向量曾經被重複地發現過好幾次[6]。它等價於天體力學中無因次的離心率向量[7]。發展至今,在物理學裏,有許多各種各樣的 LRL 向量的推廣定義;牽涉到狹義相對論,或電磁場,甚至於不同類型的連心力。
目录
[隐藏]概論[编辑]
在一個物理系統裏,在任意保守的連心力的作用下(參閱保守力),一個粒子的運動,都會擁有至少四個運動常數;能量與角動量 的三個分量皆為運動常數。粒子的軌道被限制於一個平面。粒子的動量
的三個分量皆為運動常數。粒子的軌道被限制於一個平面。粒子的動量  和從力中心點的位置到粒子位置的位移
和從力中心點的位置到粒子位置的位移  (參閱圖 1)。粒子的運動平面垂直於角動量
(參閱圖 1)。粒子的運動平面垂直於角動量  。用方程式表示,
。用方程式表示, 。
。
 ,也肯定地包含於粒子的運動平面。可是,只有當連心力遵守平方反比定律時,
,也肯定地包含於粒子的運動平面。可是,只有當連心力遵守平方反比定律時,  才是常數向量[1]。對於別種連心力,
才是常數向量[1]。對於別種連心力,  不是常數向量,其大小與方向都會改變。假若連心力近似地遵守平方反比定律,則
不是常數向量,其大小與方向都會改變。假若連心力近似地遵守平方反比定律,則  的大小近似常數,而方向會緩慢地轉動。對於所有的連心力,可以定義一個廣義 LRL 向量,但是,這廣義向量通常並沒有解析解,假若有,也會是一個非常複雜的函數[8][9]。
的大小近似常數,而方向會緩慢地轉動。對於所有的連心力,可以定義一個廣義 LRL 向量,但是,這廣義向量通常並沒有解析解,假若有,也會是一個非常複雜的函數[8][9]。歷史[编辑]
在重要的克卜勒問題中, LRL 向量 是一個運動常數,時常用來描述天文軌道,例如行星的運動。然而,物理學家對它並不熟悉,這很可能是因為與動量與角動量相比,它比較難以被直覺地理解內涵的物理。因此,在過去三個世紀裏,它曾被重複地發現過許多次[6]。1710 年,在一個不著名的義大利學刊裏,雅各布·赫爾曼最先發表了關於 LRL 向量的論文。在推導一個軌道方程式的過程中,他計算出 LRL 向量的大小,
是一個運動常數,時常用來描述天文軌道,例如行星的運動。然而,物理學家對它並不熟悉,這很可能是因為與動量與角動量相比,它比較難以被直覺地理解內涵的物理。因此,在過去三個世紀裏,它曾被重複地發現過許多次[6]。1710 年,在一個不著名的義大利學刊裏,雅各布·赫爾曼最先發表了關於 LRL 向量的論文。在推導一個軌道方程式的過程中,他計算出 LRL 向量的大小,  是保守的[10];並且推導出此案例與橢圓軌道離心率的關係。稍後,赫爾曼把這結果告訴约翰·白努利,他的恩師。白努利又更進一步地推導出 LRL 向量的方向。這樣,LRL 向量得到了它的現代形式[11]。所以,不容質疑地,LRL 向量是赫爾曼和白努利共同發現的。
是保守的[10];並且推導出此案例與橢圓軌道離心率的關係。稍後,赫爾曼把這結果告訴约翰·白努利,他的恩師。白努利又更進一步地推導出 LRL 向量的方向。這樣,LRL 向量得到了它的現代形式[11]。所以,不容質疑地,LRL 向量是赫爾曼和白努利共同發現的。在那個世紀末尾,皮埃爾-西蒙·拉普拉斯又重新地發現了 LRL 向量的保守性;稍微不同地,他的導引使用的是分析方法,而不是幾何方法[12]。十九世紀中葉,威廉·哈密頓推導出全等的離心率向量[7]。他用離心率向量來證明,在平方反比連心力作用下,速端曲線顯示出,粒子動量向量的頭部呈圓形移動[13] (參閱圖 3)。二十世紀初,約西亞·吉布斯,應用向量分析,推導出同樣的向量[14]。後來,卡爾·龍格將吉布斯的導引,納入自己所寫的一本廣受歡迎的,關於向量的,德文教科書內,成為其中的一個例題[15] 。1924 年,威爾漢·冷次發表了一篇關於氫原子的舊量子論的論文。在這篇論文中,他引用龍格所寫的教科書的例題為參考[16]。1926 年, 沃爾夫岡·包立用 LRL 向量與矩陣力學,而不是薛丁格方程式,來推導氫原子的光譜[3]。這傑作說服了大多數物理學家,使他們覺得量子力學理論是正確的。
數學定義[编辑]
 可以表達為
可以表達為 ;
;
 是比例常數,
是比例常數, 是單位向量,
是單位向量, 是粒子的位置向量,
是粒子的位置向量, 是
是  的大小。
的大小。感受到此力的作用,一個粒子的軌道運動,其 LRL 向量的數學定義方程式為
 ;
;
 是粒子的質量,
是粒子的質量, 是動量,
是動量,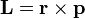 是角動量。
是角動量。由於平方反比連心力為保守力,能量
 是運動常數:
是運動常數: 。
。
 也是保守的,可以決定粒子移動平面的取向。因為
也是保守的,可以決定粒子移動平面的取向。因為  與
與  都垂直於
都垂直於  ,所以,LRL 向量
,所以,LRL 向量  垂直於角動量;
垂直於角動量;  包含於軌道的平面。
包含於軌道的平面。這個單獨粒子的 LRL 向量定義,也可以延伸至像克卜勒問題一類的二體問題,只需要設定質量
 為二個物體的約化質量,設定位置向量
為二個物體的約化質量,設定位置向量  為二個物體之間的相對位置向量。
為二個物體之間的相對位置向量。同樣的運動常數可以有很多種不同的表述.最常見的一種牽涉到離心率向量。定義離心率向量
 為 LRL 向量與
為 LRL 向量與  的除商:
的除商: 。
。
克卜勒軌道導引[编辑]
克卜勒問題的運動軌道,其形狀與取向,可以用 LRL 向量決定[1]。 與
與  的內積為
的內積為 ;
;
 為
為  與
與  之間的夾角。
之間的夾角。置換其三重積,
 。
。
 。
。
 。
。
 為
為 。
。
 與自己的內積為
與自己的內積為 。
。
 。
。
 是能量
是能量  的函數:
的函數: 。
。
 是負值的(束縛軌道),則離心率小於 1 ,這軌道是橢圓形軌道。相反地,假若能量是正值的(非束縛軌道,又稱為散射軌道)則離心率大於 1 ,這軌道是雙曲線軌道。最後,假若能量等於零,則離心率等於 1 ,這軌道是拋物線軌道。對於所有狀況, LRL 向量與圓錐曲線的對稱軸平行,而且從力中心點指向近拱點。
是負值的(束縛軌道),則離心率小於 1 ,這軌道是橢圓形軌道。相反地,假若能量是正值的(非束縛軌道,又稱為散射軌道)則離心率大於 1 ,這軌道是雙曲線軌道。最後,假若能量等於零,則離心率等於 1 ,這軌道是拋物線軌道。對於所有狀況, LRL 向量與圓錐曲線的對稱軸平行,而且從力中心點指向近拱點。圓形的速端曲線[编辑]
 與角動量
與角動量  的保守性來證明[13][6]。計算
的保守性來證明[13][6]。計算  與
與  的叉積:
的叉積: 。
。
 與 z-軸同方向,x-軸與半長軸同軸。則
與 z-軸同方向,x-軸與半長軸同軸。則 。
。
 的頭部被限制於一個圓圈;圓圈的半徑為
的頭部被限制於一個圓圈;圓圈的半徑為  ,圓心為
,圓心為  。如圖 3 所示,圓形的動量速端曲線 毫無疑問地顯示出克卜勒問題的對稱性。
。如圖 3 所示,圓形的動量速端曲線 毫無疑問地顯示出克卜勒問題的對稱性。夾角
 的一邊是點 2 與圓心的連線,另一邊是負 py-軸。很顯然地,離心率等於
的一邊是點 2 與圓心的連線,另一邊是負 py-軸。很顯然地,離心率等於  。為了簡化運算,在這裏提出一個很有用的變量
。為了簡化運算,在這裏提出一個很有用的變量  。
。運動常數與超級可積分性[编辑]
在克卜勒問題裏,兩個向量 ,
, 與一個純量
與一個純量  加起來一共有七個常數純量。它們之間的相關性表達於
加起來一共有七個常數純量。它們之間的相關性表達於  與
與  這兩個公式。因為
這兩個公式。因為  的大小可以由角動量
的大小可以由角動量  與能量
與能量  計算出來。再者,
計算出來。再者, 必須垂直於
必須垂直於  。所以,
。所以, 只能貢獻 1 個運動常數。
只能貢獻 1 個運動常數。由於有上述兩個關係公式,這物理系統一共有五個獨立的運動常數。這結果與設定粒子軌道所需的六個初始條件(粒子的初始位置向量與初始速度向量,每一個向量有三個分量)相符合,原因是運動常數不涉及初始時間(視六個初始條件函數的參數為自變量初始時間。用其中的一個初始條件函數除去這自變量;將此初始條件函數當作一個自變量,則剰餘五個初始條件函數,函數的參數為新自變量)。
因為運動方程式是二階微分方程,一個擁有
 自由度的物理系統,需要
自由度的物理系統,需要  個初始條件來設定解答。由於運動常數不涉及初始時間,這物理系統最多只能擁有
個初始條件來設定解答。由於運動常數不涉及初始時間,這物理系統最多只能擁有  個運動常數。一個擁有超過
個運動常數。一個擁有超過  個運動常數的物理系統稱為超級可積分系統;而一個擁有
個運動常數的物理系統稱為超級可積分系統;而一個擁有  個運動常數的物理系統稱為最大超級可積分系統[17]。哈密頓-亞可比方程式的解答,採用任意一種坐標系統,最多只能求得
個運動常數的物理系統稱為最大超級可積分系統[17]。哈密頓-亞可比方程式的解答,採用任意一種坐標系統,最多只能求得  個運動常數[18]。
個運動常數[18]。克卜勒問題擁有三個自由度(
 )與五個運動常數;克卜勒問題的系統是最大超級可積分系統;採用球坐標或拋物線坐標,哈密頓-亞可比方程式都是可積分的[19];這論據,稍後會有詳細的解釋。最大超級可積分系統可以用對易關係來量子化,這論據,稍後也會又更明瞭的說明[20]。
)與五個運動常數;克卜勒問題的系統是最大超級可積分系統;採用球坐標或拋物線坐標,哈密頓-亞可比方程式都是可積分的[19];這論據,稍後會有詳細的解釋。最大超級可積分系統可以用對易關係來量子化,這論據,稍後也會又更明瞭的說明[20]。在微擾勢下的系統演化[编辑]
只有在一個標準的平方反比連心力下,粒子的 LRL 向量 是保守的。對於大多數的實際問題,例如行星運動,作用力並不會完全地遵守平方反比定律,而可能會含有別種微擾的連心力;稱其負值不定積分為微擾勢,標記為
是保守的。對於大多數的實際問題,例如行星運動,作用力並不會完全地遵守平方反比定律,而可能會含有別種微擾的連心力;稱其負值不定積分為微擾勢,標記為  。在這種狀況下,LRL 向量會緩慢地轉動於軌道平面,相應於軌道的慢進動。假若微擾勢
。在這種狀況下,LRL 向量會緩慢地轉動於軌道平面,相應於軌道的慢進動。假若微擾勢  為一個保守的連心勢,也就是說,總能量
為一個保守的連心勢,也就是說,總能量  與角動量
與角動量  都是保守的,則粒子的運動 仍舊包含於一個垂直於
都是保守的,則粒子的運動 仍舊包含於一個垂直於  的平面,大小
的平面,大小  仍舊是保守的。微擾勢
仍舊是保守的。微擾勢  可以是任何形式的函數。但是,微擾值應該顯著地弱於主連心勢。一個典形的微擾勢可以表示為
可以是任何形式的函數。但是,微擾值應該顯著地弱於主連心勢。一個典形的微擾勢可以表示為 ;
;
 是微擾勢強度,整數
是微擾勢強度,整數  。
。用正則微擾理論與作用量-角度座標,可以直接地推導出 LRL 向量的轉動率是[1]
 ;
;
 是軌道週期,恆等式
是軌道週期,恆等式  轉變時間積分為角積分(如圖 5 )。角括號表達式
轉變時間積分為角積分(如圖 5 )。角括號表達式  是週期平均微擾勢;也就是說,物體繞軌道一個公轉 的平均微擾勢。取平均值可以減少轉動率的變動。
是週期平均微擾勢;也就是說,物體繞軌道一個公轉 的平均微擾勢。取平均值可以減少轉動率的變動。這方法曾經被用來證實愛因斯坦的廣義相對論。廣義相對論在常見的牛頓萬有引力項目外,又添加了一項小的反立方微擾[21] 。
 。
。
 與
與  的關係公式
的關係公式 ,
,
 。
。
帕松括號[编辑]
角動量 的三個分量
的三個分量  的帕松括號是[1]
的帕松括號是[1] ;
;
 代表直角座標系的三個座標
代表直角座標系的三個座標  ,
, 是列維-奇維塔符號;在這裏,為了避免與力強度的標記
是列維-奇維塔符號;在這裏,為了避免與力強度的標記  發生混淆,採用
發生混淆,採用  為連加運算的指標。
為連加運算的指標。定義一個與 LRL 向量成比例的向量
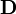 為
為 。
。
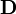 與角動量
與角動量  的單位相同。
的單位相同。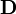 與
與  的帕松括號為[26]
的帕松括號為[26] 。
。
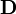 與自己的帕松括號跟總能量
與自己的帕松括號跟總能量  的正負號有關;也就是說,跟是否總能量
的正負號有關;也就是說,跟是否總能量  是正值(在平方反比連心力作用下,產生開放的雙曲線軌道),或負值(在平方反比連心力作用下,產生閉合地橢圓軌道)有關。假若總能量
是正值(在平方反比連心力作用下,產生開放的雙曲線軌道),或負值(在平方反比連心力作用下,產生閉合地橢圓軌道)有關。假若總能量  是正值,帕松括號是
是正值,帕松括號是 。
。
 是負值,帕松括號是
是負值,帕松括號是 。
。
 ,
, ,
, ,
,
 是負值,則可確定克卜勒問題的對稱群是四維的旋轉群 SO(4) 。
是負值,則可確定克卜勒問題的對稱群是四維的旋轉群 SO(4) 。假若總能量
 是負值,卡西米爾不變量
是負值,卡西米爾不變量  定義為
定義為 ,
, 。
。
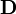 的每一個分量的帕松括號皆為零:
的每一個分量的帕松括號皆為零: 。
。
 的每一個分量的帕松括號皆為零:
的每一個分量的帕松括號皆為零: 。
。
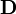 與
與  永遠是互相垂直的,
永遠是互相垂直的, 明顯地是零。可是,另外一個不變量
明顯地是零。可是,另外一個不變量 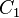 只跟質量
只跟質量  、力強度
、力強度  、總能量
、總能量  有關。不變量
有關。不變量 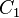 分別與
分別與  ,
,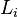 的帕松括號等於零的導引並不明顯。這不變量
的帕松括號等於零的導引並不明顯。這不變量 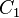 使得只用到量子力學的正則對易關係,就可以推導出類氫原子的原子能級,而不必用到的薛丁格方程式。
使得只用到量子力學的正則對易關係,就可以推導出類氫原子的原子能級,而不必用到的薛丁格方程式。氫原子量子力學[编辑]
帕松括號提供了一個簡易的方法來正則量子化經典系統。兩個量子算符的對易關係等於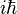 乘以對應的經典變量[27]。經過這量子化程序,計算克卜勒問題的卡西米爾算符
乘以對應的經典變量[27]。經過這量子化程序,計算克卜勒問題的卡西米爾算符  的本徵值 ,沃爾夫岡·包利成功地推導出類氫原子的原子能級(參閱圖 6 ),以及其發射光譜[3]。早在薛丁格方程式成立之前[28],包利就研究出這重要的結果!
的本徵值 ,沃爾夫岡·包利成功地推導出類氫原子的原子能級(參閱圖 6 ),以及其發射光譜[3]。早在薛丁格方程式成立之前[28],包利就研究出這重要的結果!LRL 向量
 的量子算符有一個奧妙之處,那就是動量算符與角動量算符並不對易。動量與角動量的叉積必須仔細地加以定義[26]。LRL 向量的直角座標分量典型地定義為
的量子算符有一個奧妙之處,那就是動量算符與角動量算符並不對易。動量與角動量的叉積必須仔細地加以定義[26]。LRL 向量的直角座標分量典型地定義為 ;
;
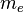 是電子的質量,常數
是電子的質量,常數  ,
, 是單位電荷量,
是單位電荷量,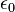 是真空電容率。
是真空電容率。這定義有一個特性:指標
 是對稱的,指標
是對稱的,指標  的互換不會改變
的互換不會改變 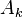 的數值。表示為向量形式,
的數值。表示為向量形式, 。
。
 。
。
 向量成正比的
向量成正比的 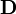 向量則是
向量則是 。
。
經過一番繁冗的運算,可以求得對易關係:
 、
、 、
、 、
、 。
。
 、
、 。
。
 。
。
 和
和  的對易關係是
的對易關係是 。
。
 、
、 、
、 ;
;
 是角量子數為
是角量子數為  、磁量子數為
、磁量子數為  的本徵態,
的本徵態, 是常數係數。
是常數係數。經過一番運算,
 和
和  的對易算符作用於
的對易算符作用於  的結果是
的結果是![\begin{align}\{J_{+1},\,J_{ - 1}\}|l,\,m\rangle & = - m[(2l-1)\mathfrak{C}_l^2-(2l+3)\mathfrak{C}_{l+1}^2]|l,\,m\rangle \\
& = - \hbar L_3|l,\,m\rangle= - m\hbar^2 \\
\end{align}](http://upload.wikimedia.org/math/3/d/b/3dbe69917d0b91f7393d414a57dfc361.png) 。
。
 的遞迴關係是
的遞迴關係是 。
。
 是非負值,則為了滿足上述公式,
是非負值,則為了滿足上述公式, 。再假設
。再假設  的最大值是
的最大值是  。由於態向量
。由於態向量  不存在,
不存在, 。因此,
。因此, 。設定
。設定  ,稍加計算,
,稍加計算, 的一般方程式為
的一般方程式為 。
。
 就是跟能級有關的主量子數。先計算
就是跟能級有關的主量子數。先計算 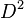 :
:![\begin{align}D^2|n,\,l,\,m\rangle & =[J_{+1}J_{ - 1}+J_{ - 1}J_{+1}+J_0^2]|n,\,l,\,m\rangle \\
& =(n^2 - l^2 - l - 1)\hbar^2|n,\,l,\,m\rangle \\
\end{align}](http://upload.wikimedia.org/math/0/2/3/02362a8b5d84406949f747a4682801fc.png) 。
。
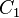 作用於態向量
作用於態向量  可以得到
可以得到 。
。
 的本徵值是
的本徵值是  。重點是,這些本徵值跟量子數
。重點是,這些本徵值跟量子數  、
、 無關,這造成了原子能階的簡併[26] :
無關,這造成了原子能階的簡併[26] : 。
。
保守性與對稱性[编辑]
在克卜勒問題裏,LRL 向量的保守性 對應於系統的一種微妙的對稱性。在經典力學裏,對稱性可以由連續運算顯示出來;這連續運算可以將一個軌道映射至另外一個軌道,而同時保持系統的能量不變。在量子力學裏,連續運算將同能級原子軌域混合在一起,也就是說,(簡併原子能級)。通常,對於每一個對稱性都會存在有一個保守量[1]。例如,連心力系統必對稱於旋轉群 SO(3) ;因而指引出角動量
 的保守性。在經典力學裏,整個系統的旋轉不會影響軌道的能量。在量子力學裏,假若旋轉只混合角量子數相同的球諧函數,則系統的能量不會改變。
的保守性。在經典力學裏,整個系統的旋轉不會影響軌道的能量。在量子力學裏,假若旋轉只混合角量子數相同的球諧函數,則系統的能量不會改變。平方反比連心力系統的對稱性是更高維與更微妙的。這奇特的對稱性是由角動量
 與 LRL 向量
與 LRL 向量  的雙重保守性造成的;這保證了氫原子的能級跟角量子數
的雙重保守性造成的;這保證了氫原子的能級跟角量子數  、磁量子數
、磁量子數  無關。由於對稱性運算必須發生於更高維空間,使得這對稱性更加的微妙;這類的對稱性常稱為隱祕對稱性[29]。在經典力學裏,克卜勒問題的高維對稱性 容許連續的改變軌道.只要保持能量不變,而角動量可以改變;換句話說,同能量,不同角動量(離心率)的軌道可以互相的連續變換。在量子力學裏,這對應著不同角量子數
無關。由於對稱性運算必須發生於更高維空間,使得這對稱性更加的微妙;這類的對稱性常稱為隱祕對稱性[29]。在經典力學裏,克卜勒問題的高維對稱性 容許連續的改變軌道.只要保持能量不變,而角動量可以改變;換句話說,同能量,不同角動量(離心率)的軌道可以互相的連續變換。在量子力學裏,這對應著不同角量子數  與磁量子數
與磁量子數  的軌域的混合,例如
的軌域的混合,例如  與
與  原子軌域的混合。這種混合是不能用普通的三維平移運算或旋轉運算達成的。可是,這種混合等價於高維度空間的旋轉。
原子軌域的混合。這種混合是不能用普通的三維平移運算或旋轉運算達成的。可是,這種混合等價於高維度空間的旋轉。在一個束縛 (bounded) 系統裏,能量是負值的,這高維對稱群是 SO(4) ;特性是四維向量的長度保持不變:
 。
。
 相同的軌域的混合。隨後,華倫泰·巴格曼注意到,跟 LRL 向量成比例的向量
相同的軌域的混合。隨後,華倫泰·巴格曼注意到,跟 LRL 向量成比例的向量 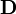 與角動量
與角動量  的帕松括號形成 SO(4) 的李代數[5]。簡單地說,
的帕松括號形成 SO(4) 的李代數[5]。簡單地說,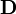 與
與  的六個物理量對應於在四維空間裏的六個保守的角動量分量,相伴於在四維空間裏的六個合法的簡單旋轉(從四個軸中,選兩個軸為旋轉軸。一共有六種可能)。這結論並不意示宇宙是一個三維球面;而只是說,這個特別的物理問題(克卜勒問題),在數學上,等價於移動於三維球面的一個自由粒子。
的六個物理量對應於在四維空間裏的六個保守的角動量分量,相伴於在四維空間裏的六個合法的簡單旋轉(從四個軸中,選兩個軸為旋轉軸。一共有六種可能)。這結論並不意示宇宙是一個三維球面;而只是說,這個特別的物理問題(克卜勒問題),在數學上,等價於移動於三維球面的一個自由粒子。在一個非束縛 (unbound) ,散射系統裏,能量是正值的,對應的高維對稱群是 SO(3,1) ;其特性是保持四維矢量的閔考斯基長度不變:
 。
。
旋轉對稱性在四維空間[编辑]
 ;其中,
;其中,  代表三維位置向量
代表三維位置向量  的直角座標。三維動量
的直角座標。三維動量  與三維單位球的四維向量
與三維單位球的四維向量 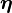 的關係為
的關係為 ;
;
 是新的 w-軸的單位向量。
是新的 w-軸的單位向量。很簡單地,可以核對
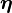 也是一個單位向量:
也是一個單位向量: 。
。
 至
至  的映射有一個獨特唯一的逆反;例如,動量
的映射有一個獨特唯一的逆反;例如,動量  的 x-軸分量是
的 x-軸分量是 。
。
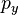 與
與 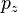 也有類似的公式。換句話說,三維動量向量
也有類似的公式。換句話說,三維動量向量  是四維單位向量
是四維單位向量  的球極平面投影,其比例因子為
的球極平面投影,其比例因子為 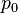 。
。選擇一個合適的直角座標,使 z-軸與角動量
 同直線,使動量的速端曲線的取向如同圖 7 ,圓心包含於 y-軸。這樣,不失廣義性,就可以觀察到這旋轉對稱性。由於粒子的運動包含於一個平面,
同直線,使動量的速端曲線的取向如同圖 7 ,圓心包含於 y-軸。這樣,不失廣義性,就可以觀察到這旋轉對稱性。由於粒子的運動包含於一個平面, 與
與  互相垂直,而且,
互相垂直,而且, 。因此,只需要專注於三維向量
。因此,只需要專注於三維向量  。圖 7 速端曲線的阿波羅尼奧斯圓 家族對應於在三維單位球
。圖 7 速端曲線的阿波羅尼奧斯圓 家族對應於在三維單位球 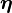 的大圓線家族。每一個大圓線與
的大圓線家族。每一個大圓線與  相交於兩個交點
相交於兩個交點  。這兩個交點相對於速端曲線圖的兩點
。這兩個交點相對於速端曲線圖的兩點  。這兩個交點也是這些大圓線的共同交點。所以,這些大圓線的互相關係是一個環繞著
。這兩個交點也是這些大圓線的共同交點。所以,這些大圓線的互相關係是一個環繞著  -軸的簡單旋轉(參閱圖 8 )。以
-軸的簡單旋轉(參閱圖 8 )。以  -軸為轉軸,每一個大圓線的位置是從
-軸為轉軸,每一個大圓線的位置是從  -平面旋轉
-平面旋轉  角。
角。取任意一個大圓線
 最大值的一點,其坐標為
最大值的一點,其坐標為  。那麼,
。那麼, 、
、 、
、 。
。
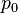 的值,可以得到
的值,可以得到 。
。
 。
。
 是緯度
是緯度  的正弦函數。
的正弦函數。由於圖 7 的動量的速端曲線對應於
 三維單位球的大圓線的球極平面投影,而這速端曲線家族的成員都擁有相同的能量。所以,這旋轉的對稱性使所有能量相同的軌道都能夠互相變換。但是,這旋轉正交於通常的三維旋轉,因為它涉及了第四維
三維單位球的大圓線的球極平面投影,而這速端曲線家族的成員都擁有相同的能量。所以,這旋轉的對稱性使所有能量相同的軌道都能夠互相變換。但是,這旋轉正交於通常的三維旋轉,因為它涉及了第四維  。高維度的對稱性是克卜勒問題對應於 LRL 向量的一個特徵。
。高維度的對稱性是克卜勒問題對應於 LRL 向量的一個特徵。採用橢圓柱坐標
 來代替四維座標
來代替四維座標 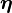 ,克卜勒問題有一個精緻的作用量-角度座標解答[34]:
,克卜勒問題有一個精緻的作用量-角度座標解答[34]: ,
, ,
, ,
, ;
;
 是亞可比橢圓函數。
是亞可比橢圓函數。克卜勒問題 LRL 向量恆定的證明[编辑]
以下幾種導引可以証明,在平方反比連心力下,LRL 向量守恆。直接證明[编辑]
假設,一個連心力 作用於一個粒子。根據牛頓第二定律,運動方程式為
作用於一個粒子。根據牛頓第二定律,運動方程式為 ;
;
 是函數,
是函數, 為粒子的位置,
為粒子的位置, 是動量,
是動量, 是時間。
是時間。由於在連心力下,角動量
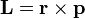 是恆定的,
是恆定的, 。
。
![\frac{\mathrm{d}}{\mathrm{d}t}\left( \mathbf{p}\times\mathbf{L} \right)=\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} \times \mathbf{L} = f(\mathbf{r}) \mathbf{\hat{r}} \times \left( \mathbf{r} \times m \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right) = f(\mathbf{r}) \frac{m}{r} \left[ \mathbf{r} \left(\mathbf{r} \cdot \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right) - r^{2} \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \right]](http://upload.wikimedia.org/math/9/0/7/907ef93300713cf01374e4e3b12fef91.png) 。
。
 ,
,
![\frac{\mathrm{d}}{\mathrm{d}t} \left( \mathbf{p} \times \mathbf{L} \right) =
- m f(\mathbf{r}) r^{2} \left[ \frac{1}{r} \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} - \frac{\mathbf{r}}{r^{2}} \frac{\mathrm{d}r}{\mathrm{d}t}\right] = - m f(\mathbf{r}) r^{2} \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\mathbf{r}}{r}\right)](http://upload.wikimedia.org/math/0/a/f/0afffe761d7254a81ff308b4ad7e0bcc.png) 。
。
 ,
, 。
。
 是恆定的:
是恆定的: 。
。
哈密頓-亞可比方程式[编辑]
哈密頓-亞可比方程式的可分性也可以用推導出 LRL 向量的恆定性[19][35]。採用拋物線座標 ,定義
,定義 、
、 ;
;
 是直角座標,
是直角座標, 是軌道的徑向距離:
是軌道的徑向距離: 。
。
 、
、 。
。
 ;
;
 分別是廣義座標
分別是廣義座標  的共軛動量。
的共軛動量。由於克卜勒問題的勢函數只跟廣義座標有關,哈密頓量是個能量運動常數,
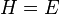 。稍加編排,可以得到
。稍加編排,可以得到 。
。
 :
: 、
、 。
。
 分量,
分量, 。
。
 ,則
,則 。
。
 。
。
 也是運動常數:
也是運動常數: 。
。
諾特定理[编辑]
LRL 向量的保守性與前面所提的旋轉對稱性,兩者之間的關係,可以用諾特定理來做連結分析。諾特定理也可以用來辨明 LRL 向量是運動常數。諾特定理表明[36]:在一個物理系統裏,對於廣義坐標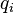 的微小變分
的微小變分  ,假若,取至微小參數
,假若,取至微小參數  的一階,拉格朗日量
的一階,拉格朗日量  的變分
的變分 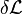 是
是 ,
,
 滿足方程式
滿足方程式 ;
;
 、
、  都是函數。
都是函數。更具體地,在一個克卜勒問題裏,試設定坐標
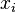 的微小變分為
的微小變分為![\delta x_i=\frac{\epsilon}{2} \left[ 2p_{i}x_{s} - x_{i}p_{s} - (\mathbf{r}\cdot \mathbf{p})\delta_{is} \right]](http://upload.wikimedia.org/math/6/a/8/6a83b9dd00a5ed4a29efaae8bd4ee51a.png) ;
;
 ,
, 與
與  分別為位置
分別為位置  與動量
與動量  的
的  -軸分量,
-軸分量, 是克羅內克爾δ,
是克羅內克爾δ, 是固定的下標。
是固定的下標。由於克卜勒問題的拉格朗日量是
 。
。
 。
。
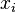 的變分,速度
的變分,速度  的變分為
的變分為![\begin{align} \delta \dot{x}_{i} & = \frac{\epsilon}{2} \left[2\dot{p}_{i} x_{s}-x_{i}\dot{p}_{s}+p_{i}\dot{x}_{s} - \frac{p^2}{m}\delta_{is} - (\mathbf{r}\cdot\dot{\mathbf{p}})\delta_{is} \right] \\
& = \frac{\epsilon}{2} \left[ - \frac{k}{r^3}x_i x_s+p_{i}\dot{x}_{s} - \frac{p^2}{m}\delta_{is} +\frac{k}{r}\delta_{is} \right] \\ \end{align}](http://upload.wikimedia.org/math/0/f/e/0fe1984aa6d84b160c69f2d66e3e940e.png) 。
。
 。
。
 和
和  的公式,經過一番繁瑣的運算,可以得到
的公式,經過一番繁瑣的運算,可以得到 。
。
 的公式,則會得到
的公式,則會得到![\Gamma=p^{2} x_{s} - p_{s}\left(\mathbf{r} \cdot \mathbf{p}\right) - \frac{mkx_{s}}{r}=\left[\mathbf{p}\times \mathbf{L} - mk\hat{\mathbf{r}}\right]_{s}](http://upload.wikimedia.org/math/3/5/9/35926edfb5aa2f3e7c641a80d790bfed.png) ;
;
 -軸分量
-軸分量  。
。李變換[编辑]
諾特定理精緻地推導出 LRL 向量的保守性。美中不足地,這導引有一個弱點:坐標變分 不只涉及了位置
不只涉及了位置  ,而且還涉及了動量
,而且還涉及了動量  [37] 。假若,使用數學家索菲斯·李創建的方法來推導,可以除去這弱點[38][39] 。具體地,定義一個李變換[29],座標
[37] 。假若,使用數學家索菲斯·李創建的方法來推導,可以除去這弱點[38][39] 。具體地,定義一個李變換[29],座標  與時間
與時間  都按照比例變換,比例是參數
都按照比例變換,比例是參數  的不同羃數:
的不同羃數: 。
。
 的大小與能量
的大小與能量  :
: 。
。
 不變。所以,離心率
不變。所以,離心率  與 LRL 向量
與 LRL 向量  的大小不變。這可以從
的大小不變。這可以從 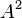 的公式觀察出:
的公式觀察出: 。
。
 的方向也會保持不變。在李變換下,克卜勒第三定律也仍舊成立:半長軸
的方向也會保持不變。在李變換下,克卜勒第三定律也仍舊成立:半長軸  與週期
與週期  形成常數
形成常數 。
。推廣至別種位勢和相對論[编辑]
LRL 向量可以推廣至其他狀況;可以用來辨認在其他狀況下的保守值。假設,一個物理系統裏,存在著電場
 ,保守的廣義 LRL 向量
,保守的廣義 LRL 向量  是[19][40]
是[19][40]![\mathcal{A} = \mathbf{A} + \frac{mq}{2} \left[ \left( \mathbf{r} \times \mathbf{E} \right) \times \mathbf{r} \right]](http://upload.wikimedia.org/math/4/5/7/4576db9227c7942bfaace2e63dd32a60.png) ;
;
 是粒子的電荷量。
是粒子的電荷量。最廣義的 LRL 向量的形式可以表達為[8]
![\mathcal{A}=\left( \frac{\partial \xi}{\partial u} \right) \left(\mathbf{p} \times \mathbf{L}\right)+\left[\xi - u \left( \frac{\partial \xi}{\partial u} \right)\right] L^{2} \mathbf{\hat{r}}](http://upload.wikimedia.org/math/1/8/3/18307ada2ebd1751615b32dfa94e41b1.png) ;
;
 (參閱伯特蘭定理),
(參閱伯特蘭定理), ,角
,角  定義為
定義為 ;
;
 是勞侖茲因子。
是勞侖茲因子。如同前面所提,計算
 與
與  的叉積,可以得到一個保守的副法線向量
的叉積,可以得到一個保守的副法線向量  :
: 。
。
 :
: 。
。
 ,力子的角動量是保守的,粒子的運動包含於一個平面。請注意,
,力子的角動量是保守的,粒子的運動包含於一個平面。請注意, 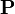 與
與  不是一定互相垂直的。保守的並矢張量可以表達為一個簡單的形式:
不是一定互相垂直的。保守的並矢張量可以表達為一個簡單的形式: 。
。
 ;
;
 是自然振率。
是自然振率。別種比例與表述[编辑]
不同於動量與角動量,並沒有學術界一致認同的 LRL 向量定義;在科學文獻裏,存在有幾種不同的比例因子與符號。前面所述的定義是最普遍的定義。另外一種常見的定義,將 除以常數
除以常數  ;這樣,可以得到一個無因次的離心率向量
;這樣,可以得到一個無因次的離心率向量  :
: ;
;
 是速度。
是速度。離心率向量
 的方向與
的方向與  相同,大小是軌道的離心率。
相同,大小是軌道的離心率。別種比例的版本也可能會用到。例如,將
 除以
除以  :
: ,
,
 除以
除以 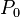 :
: 。
。
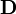 與角動量
與角動量  的單位相同。在非常稀有的狀況, LRL 向量的正負號會改變。這些,都不會影響它是運動常數的事實。
的單位相同。在非常稀有的狀況, LRL 向量的正負號會改變。這些,都不會影響它是運動常數的事實。另外一個保守的向量是副法線向量
 。威廉·哈密頓曾經研究過這向量[7]。
。威廉·哈密頓曾經研究過這向量[7]。 。
。
 是
是  叉積
叉積  (參閱圖 4 )。兩個向量
(參閱圖 4 )。兩個向量  與
與  可以結合起來形成一個保守的並矢張量
可以結合起來形成一個保守的並矢張量  [8]:
[8]: ;
;
 與
與  是任意比例常數,符號
是任意比例常數,符號  表示張量積。展開這公式為
表示張量積。展開這公式為 。
。
 與
與  可以視為保守的張量
可以視為保守的張量  的主軸,也就是說,按比例的特徵向量。由於
的主軸,也就是說,按比例的特徵向量。由於 與
與  都垂直於
都垂直於  ,張量
,張量  垂直於角動量
垂直於角動量  :
: 。
。
參閱[编辑]
參考文獻[编辑]
- ^ 1.0 1.1 1.2 1.3 1.4 1.5 Goldstein, H. Classical Mechanics 2nd edition. Addison Wesley. 1980: 102–105,410–422,536–538.
- ^ 阿諾爾德, 弗拉基米爾. Mathematical Methods of Classical Mechanics, 2nd ed.. New York: Springer-Verlag. 1989: 38. ISBN 0-387-96890-3.
- ^ 3.0 3.1 3.2 包立, 沃爾夫岡, Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik, Zeitschrift für Physik. 1926, 36: 336–363
- ^ 4.0 4.1 Fock, V., Zur Theorie des Wasserstoffatoms, Zeitschrift für Physik. 1935, 98: 145–154
- ^ 5.0 5.1 巴格曼, 華倫泰, Zur Theorie des Wasserstoffatoms: Bemerkungen zur gleichnamigen Arbeit von V. Fock, Zeitschrift für Physik. 1936, 99: 576–582
- ^ 6.0 6.1 6.2 Goldstein, H., Prehistory of the Runge–Lenz vector, American Journal of Physics. 1975, 43: 735–738
Goldstein, H., More on the prehistory of the Runge–Lenz vector, American Journal of Physics. 1976, 44: 1123–1124 - ^ 7.0 7.1 7.2 哈密頓, 威廉, Applications of Quaternions to Some Dynamical Questions, Proceedings of the Royal Irish Academy. 1847, 3: Appendix III
- ^ 8.0 8.1 8.2 Fradkin, D. M., Existence of the Dynamic Symmetries O4 and SU3 for All Classical Central Potential Problems, Progress of Theoretical Physics. 1967, 37: 798–812
- ^ Yoshida, T, Two methods of generalisation of the Laplace–Runge–Lenz vector, European Journal of Physics. 1987, 8: 258–259
- ^ 赫爾曼, 雅各布, Unknown title, Giornale de Letterati D'Italia. 1710, 2: 447–467
赫爾曼, 雅各布, Extrait d'une lettre de M. Herman à M. Bernoulli datée de Padoüe le 12. Juillet 1710, Histoire de l'academie royale des sciences (Paris). 1710, 1732: 519–521 - ^ 白努利, 約翰, Extrait de la Réponse de M. Bernoulli à M. Herman datée de Basle le 7. Octobre 1710, Histoire de l'academie royale des sciences (Paris). 1710, 1732: 521–544
- ^ 拉普拉斯, 皮埃爾-西蒙. Traité de mécanique celeste. 1799: Tome I, Premiere Partie, Livre II, pp.165ff.
- ^ 13.0 13.1 哈密頓, 威廉, The hodograph or a new method of expressing in symbolic language the Newtonian law of attraction, Proceedings of the Royal Irish Academy. 1847, 3: 344-353
- ^ 吉布斯, 約西亞; Wilson E. B. Vector Analysis. New York: Scribners. 1901: p. 135.
- ^ 龍格, 卡爾. Vektoranalysis. Leipzig: Hirzel. 1919: Volume I.
- ^ 冷次, 威爾漢, Über den Bewegungsverlauf und Quantenzustände der gestörten Keplerbewegung, Zeitschrift für Physik. 1924, 24: 197–207
- ^ Evans, N. W., Superintegrability in classical mechanics, Physical Review A. 1990, 41: 5666–5676
- ^ 索末菲, 阿諾. Atomic Structure and Spectral Lines. London: Methuen. 1923: 118.
- ^ 19.0 19.1 19.2 朗道, 列夫; Lifshitz E. M. Mechanics 3rd edition. Pergamon Press. 1976: p. 154. ISBN 0-08-021022-8 (hardcover) and ISBN 0-08-029141-4 (softcover).
- ^ Evans, N. W., Group theory of the Smorodinsky–Winternitz system, Journal of Mathematical Physics. 1991, 32: 3369–3375
- ^ 21.0 21.1 愛因斯坦, 阿爾伯特, Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie, Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1915, 1915: 831–839
- ^ 勒維耶, Lettre de M. Le Verrier à M. Faye sur la Théorie de Mercure et sur le Mouvement du Périhélie de cette Planète, Comptes Rendus de l'Academie de Sciences (Paris). 1859, 49: 379–383
- ^ Will, C. M. General Relativity, an Einstein Century Survey SW Hawking and W Israel, eds. Cambridge: Cambridge University Press. 1979: Chapter 2.
- ^ 派斯, 亞伯拉罕. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. 1982.
- ^ Roseveare, N. T. Mercury's Perihelion from Le Verrier to Einstein. Oxford University Press. 1982.
- ^ 26.0 26.1 26.2 Bohm, A. Quantum Mechanics: Foundations and Applications 2nd edition. Springer Verlag. 1986: 208–222.
- ^ 狄拉克, 保羅. Principles of Quantum Mechanics, 4th revised edition. Oxford University Press. 1958.
- ^ 薛丁格, 埃爾文, Quantisierung als Eigenwertproblem, Annalen der Physik. 1926, 384: 361–376
- ^ 29.0 29.1 Prince, GE; Eliezer CJ, On the Lie symmetries of the classical Kepler problem, Journal of Physics A: Mathematical and General. 1981, 14: 587–596
- ^ 30.0 30.1 Bander, M; Itzykson C, Group Theory and the Hydrogen Atom (I), Reviews of Modern Physics. 1966, 38: 330–345
- ^ Bander, M; Itzykson C, Group Theory and the Hydrogen Atom (II), Reviews of Modern Physics. 1966, 38: 346–358
- ^ Rogers, HH, Symmetry transformations of the classical Kepler problem, Journal of Mathematical Physics. 1973, 14: 1125–1129
- ^ Guillemin, V; Sternberg S. Variations on a Theme by Kepler. American Mathematical Society Colloquium Publications, volume 42. 1990. ISBN 0-8218-1042-1.
- ^ Lakshmanan, M; Hasegawa H, On the canonical equivalence of the Kepler problem in coordinate and momentum spaces, Journal of Physics A, 17: L889–L893
- ^ Dulock, VA; McIntosh HV, On the Degeneracy of the Kepler Problem, Pacific Journal of Mathematics. 1966, 19: 39–55
- ^ Lévy-Leblond, JM, Conservation Laws for Gauge-Invariant Lagrangians in Classical Mechanics, American Journal of Physics. 1971, 39: 502–506
- ^ Gonzalez-Gascon, F, Notes on the symmetries of systems of differential equations, Journal of Mathematical Physics. 1977, 18: 1763–1767
- ^ 李, 索菲斯. Vorlesungen über Differentialgleichungen. Leipzig: Teubner. 1891.
- ^ Ince, EL. Ordinary Differential Equations. New York: Dover (1956 reprint). 1926: 93–113.
- ^ Redmond, P. J., Generalization of the Runge–Lenz Vector in the Presence of an Electric Field, Physical Review. 1964, 133: B1352–B1353
- Leach, P.G.L.; G.P. Flessas, Generalisations of the Laplace–Runge–Lenz vector, J. Nonlinear Math. Phys.. 2003, 10: 340–423, arXiv:math-ph/0403028
外部連結[编辑]
- 加利福尼亞大學河濱分校物理網頁:Baez, John. Mysteries of the gravitational 2-body problem.
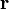 表示;而其大小則用
表示;而其大小則用 來表示。
來表示。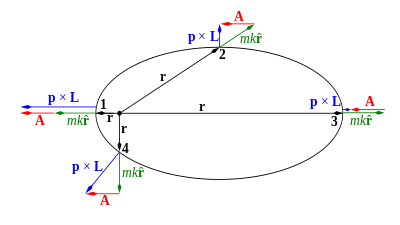
 分別用藍色與綠色表示。LRL 向量
分別用藍色與綠色表示。LRL 向量 

 (以品紅色表示),半徑是
(以品紅色表示),半徑是 
 。 假若,引性的連心力與平方反比定律稍微有點不同,類似的
。 假若,引性的連心力與平方反比定律稍微有點不同,類似的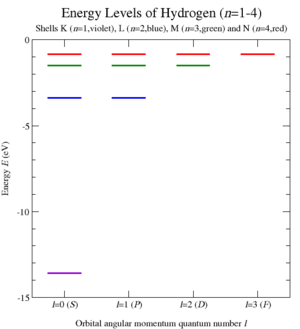

 。這一家族的速端曲線對應於一個家族的
。這一家族的速端曲線對應於一個家族的

 單位向量)到
單位向量)到  。在這圖裏的大圓線的顏色對應於它們在圖 7 的速端曲線。
。在這圖裏的大圓線的顏色對應於它們在圖 7 的速端曲線。

No comments:
Post a Comment