维基百科,自由的百科全书
 來描述的量子態,混合態則是由幾種純態依照統計機率組成的量子態。假設一個量子系統處於純態
來描述的量子態,混合態則是由幾種純態依照統計機率組成的量子態。假設一個量子系統處於純態 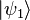 、
、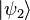 、
、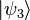 、……的機率分別為
、……的機率分別為  、
、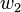 、
、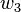 、……,則這混合態量子系統的密度算符
、……,則這混合態量子系統的密度算符  為
為 。
。
 。
。
 是一組規範正交基,則對應於密度算符的密度矩陣
是一組規範正交基,則對應於密度算符的密度矩陣  ,其每一個元素
,其每一個元素  為
為 。
。
 的期望值為
的期望值為 ,
,
 對於每一個純態的期望值
對於每一個純態的期望值 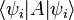 乘以其權值
乘以其權值  後的總和。
後的總和。混合態量子系統出現的案例包括,處於熱力學平衡或化學平衡的系統、製備歷史不確定或隨機變化的系統(因此不知道到底系統處於哪個純態)。假設量子系統處於由幾個糾纏在一起的亞系統所組成的純態,則雖然整個系統處於純態,每一個亞系統仍舊可能處於混合態。在量子退相干理論裏,密度算符是重要理論工具。
密度算符是一種線性算符,是自伴算符、非負算符(nonnegative operator)、跡數為1的算符。關於密度算符的數學形式論是由約翰·馮·諾伊曼與列夫·郎道各自獨立於1927年給出。[1][2]:48-55[3]
目录
[隐藏]純態與混合態[编辑]
假設一個量子系統的量子態是純態,則這量子態可以用態向量表示為 。幾種純態依照機率組成的量子態稱為混合態。例如,假設一個量子系統處於純態
。幾種純態依照機率組成的量子態稱為混合態。例如,假設一個量子系統處於純態 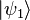 、
、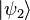 的機率都為50%,則這量子系統處於混合態。密度矩陣專門用來表示混合態。任何量子態,不管是純態,還是混合態,都可以用密度矩陣表示。
的機率都為50%,則這量子系統處於混合態。密度矩陣專門用來表示混合態。任何量子態,不管是純態,還是混合態,都可以用密度矩陣表示。混合態與疊加態的概念不同,幾種純態通過量子疊加所組成的疊加態仍舊是純態。例如,
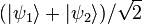 是個純態。
是個純態。光子偏振案例[编辑]
光子的兩種圓偏振態,右旋圓偏振態與左旋圓偏振態,分別以態向量 、
、 標記。光子也可能處於疊加態,例如,垂直偏振態與水平偏振態分別為
標記。光子也可能處於疊加態,例如,垂直偏振態與水平偏振態分別為  、
、 。更一般地,光子偏振所處於的疊加態可以表示為
。更一般地,光子偏振所處於的疊加態可以表示為  ;其中,
;其中, 、
、 是係數。這一般式可以表示平面偏振態、圓偏振態、橢圓偏振態等等。
是係數。這一般式可以表示平面偏振態、圓偏振態、橢圓偏振態等等。假若讓處於疊加態
 的光子通過左旋圓偏振器,則出射的光子處於左旋圓偏振態
的光子通過左旋圓偏振器,則出射的光子處於左旋圓偏振態  ;假若通過右旋圓偏振器,則出射的光子處於右旋圓偏振態
;假若通過右旋圓偏振器,則出射的光子處於右旋圓偏振態  。對於這兩種圓偏振模,光子強度都會減半,貌似意味著疊加態
。對於這兩種圓偏振模,光子強度都會減半,貌似意味著疊加態  的一半光子處於量子態
的一半光子處於量子態  ,另一半處於量子態
,另一半處於量子態  ,但這種解釋並不正確,處於量子態
,但這種解釋並不正確,處於量子態  與
與  的光子都有可能被垂直平面偏振器吸收,但是處於量子態
的光子都有可能被垂直平面偏振器吸收,但是處於量子態  的光子不會被垂直平面偏振器吸收。
的光子不會被垂直平面偏振器吸收。從白熾燈發射出的光子是一種非偏振態光子,不能用疊加態
 來描述。特別而言,與平面偏振態光子不同,它通過任何偏振器後都會失去50%強度,與圓偏振態光子不同,使用波片(waveplate)不能直接將它改變為平面偏振態光子。非偏振態光子可以描述為,處於
來描述。特別而言,與平面偏振態光子不同,它通過任何偏振器後都會失去50%強度,與圓偏振態光子不同,使用波片(waveplate)不能直接將它改變為平面偏振態光子。非偏振態光子可以描述為,處於  的機率是50%,處於
的機率是50%,處於  的機率是50%。它也可以描述為,處於垂值偏振態的機率是50%,處於水平偏振態的機率是50%。
的機率是50%。它也可以描述為,處於垂值偏振態的機率是50%,處於水平偏振態的機率是50%。非偏振態光子的量子態不是純態,而是由幾種純態依照統計機率組成。它可以由50%右旋圓偏振態與50%左旋圓偏振態組成,或者,它可以由50%垂直偏振態與50%水平偏振態組成。這兩種組合無法做實驗辨識區分,因此它們被視為同樣的混合態。密度算符含有混合態的所有資料,足夠計算任何關於混合態的可測量性質。
混合態到底源自何處?試想非偏振態光子是怎樣製成的。一種方法是利用處於動力學平衡的系統,這系統擁有很多個微觀態(microstate),伴隨每一個微觀態都有其發生的機率(波茲曼因子),它們會因熱力學漲落(thermal fluctuation)從一個微觀態變換到另一個微觀態。熱力學隨機性可以解釋白熾燈怎樣發射非偏振光子。另一種方法是引入不確定性於系統的製備程序,例如,將光束通過表面粗糙的雙折射晶體,使得光束的不同部分獲得不同偏振。第三種方法應用EPR機制,有些放射性衰變會發射兩個光子朝著反方向移動離開,這糾纏系統的量子態為
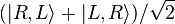 ,整個系統是處於純態,但是每一個光子亞系統的物理行為如同非偏振態光子,從分析光子亞系統的約化密度算符,可以得到這結論。
,整個系統是處於純態,但是每一個光子亞系統的物理行為如同非偏振態光子,從分析光子亞系統的約化密度算符,可以得到這結論。一般而言,混合態時常會出現於幾種純態的統計性混合(例如熱力學平衡)、製備程序的不確定性(例如光子可能移動於稍微不同路徑)、包含在糾纏系統內的亞系統(例如EPR機制)。
數學表述[编辑]
純態[编辑]
假設一個量子系統的量子態是純態,則這量子態可以用態向量表示為 ,對應的密度算符定義為[4]:309-313
,對應的密度算符定義為[4]:309-313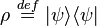 。
。
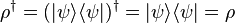 。
。
 是這量子系統的可觀察量,其本徵值為
是這量子系統的可觀察量,其本徵值為  的本徵態
的本徵態  形成一個規範正交基
形成一個規範正交基  ,則對可觀察量
,則對可觀察量  做測量得到
做測量得到  的機率
的機率 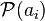 為[5]:96-99
為[5]:96-99 ;
;
 是對應於本徵態
是對應於本徵態  的投影算符,[註 1]
的投影算符,[註 1] 是跡數。
是跡數。做實驗測量可觀察量
 獲得的期望值為
獲得的期望值為 。
。
由於
 被歸一化, 密度算符的跡數為1:
被歸一化, 密度算符的跡數為1: 。
。
 ,
, ,
,
混合態[编辑]
將先前純態密度算符的定義式加以延伸,假設在一個量子系統處於純態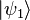 、
、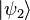 、
、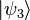 、……的機率分別為
、……的機率分別為  、
、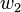 、
、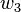 、……,則這混合態量子系統的密度算符
、……,則這混合態量子系統的密度算符  為[4]:311-313
為[4]:311-313 。
。
 ,
, 。
。
- 密度算符是自伴算符:
 。
。 - 密度算符的跡數為1:
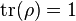 。
。 - 對可觀察量
 做測量得到
做測量得到  的機率為
的機率為 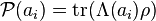 。
。 - 做實驗測量可觀察量
 獲得的期望值為
獲得的期望值為  。
。 - 密度算符是非負算符:
 。
。
 是自伴算符,它具有譜表示
是自伴算符,它具有譜表示 ;
;
 是本徵值為
是本徵值為  的本徵態,所有
的本徵態,所有  形成一個規範正交基。
形成一個規範正交基。按照自伴算符的定義,每一個本徵值
 是它自己的共軛:
是它自己的共軛: 。
。
 是非負算符,每一個本徵值
是非負算符,每一個本徵值  都是非負值。
都是非負值。由於密度算符
 的跡數為1,
的跡數為1, 。
。
 屬於這凸集,則
屬於這凸集,則  也屬於這凸集;其中,
也屬於這凸集;其中, 是係數,
是係數, 。[2]:51
。[2]:51用密度算符辨認純態[编辑]
由於純態的密度算符定義式為[4]:311-313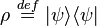 ,
,
 。
。 。
。
 。
。
 對角化後,只能有一個對角元素等於1,其它對角元素都等於0,例如,一種形式為[6]:178-183
對角化後,只能有一個對角元素等於1,其它對角元素都等於0,例如,一種形式為[6]:178-183 。
。
連續性本徵態基底[编辑]
位置是一種連續性可觀察量,具有連續性本徵值譜,用這種可觀察量的連續性本徵態為基底,密度矩陣 含有兩個位置參數
含有兩個位置參數 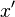 、
、 :[6]:186
:[6]:186 。
。
 的期望值為
的期望值為 。
。
複合系統[编辑]
假設密度算符為 的複合系統是由兩個亞系統
的複合系統是由兩個亞系統  、
、 組成,這兩個亞系統的物理行為分別由其對應約化密度算符(reduced density operator)
組成,這兩個亞系統的物理行為分別由其對應約化密度算符(reduced density operator)  、
、 描述:[4]:120-125,128-129
描述:[4]:120-125,128-129 、
、 ;
;
 、
、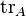 分別是對於系統
分別是對於系統 、
、 的偏跡數(partial trace)。
的偏跡數(partial trace)。這複合系統的兩個亞系統之間沒有任何關聯(沒有任何量子關聯或經典關聯),若且唯若
 是
是 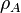 與
與  的張量積:
的張量積: 。
。
範例[编辑]
 分裂成兩道,一道的
分裂成兩道,一道的  為上旋,標記為
為上旋,標記為 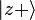 ,另一道的
,另一道的  為下旋,標記為
為下旋,標記為 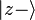 。
。z-軸方向[编辑]
- 態向量:
 。
。
- 密度矩陣:
 。
。
- 態向量:
 。
。
- 密度矩陣:
 。
。
x-軸方向[编辑]
- 態向量:
 。
。
- 密度矩陣:
 。
。
- 態向量:
 。
。
- 密度矩陣:
 。
。
y-軸方向[编辑]
- 態向量:
 。
。
- 密度矩陣:
 。
。
- 態向量:
 。
。
- 密度矩陣:
 。
。
完全隨機粒子束[编辑]
完全隨機粒子束的量子態不是純態,它可以由50%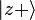 純態與50%
純態與50% 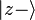 純態組成:
純態組成:![\varrho= \frac{1}{2}\varrho_{z+} + \frac{1}{2}\varrho_{z-} = \frac{1}{2}\left[\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}+\begin{pmatrix} 0 & 0 \\ 0 & 1\end{pmatrix}\right]
= \begin{pmatrix} 0.5 & 0 \\ 0 & 0.5 \end{pmatrix}](http://upload.wikimedia.org/math/0/a/5/0a56ddc97a338ba5f617fac4c9871bf3.png) 。
。
 純態與50%
純態與50%  純態組成:
純態組成:![\varrho= \frac{1}{2}\varrho_{x+} + \frac{1}{2}\varrho_{x-}= \frac{1}{2}\left[\begin{pmatrix} 0.5 & 0.5 \\ 0.5 & 0.5 \end{pmatrix}+\begin{pmatrix} 0.5 & -0.5 \\ -0.5 & 0.5 \end{pmatrix}\right]
= \begin{pmatrix} 0.5 & 0 \\ 0 & 0.5 \end{pmatrix}](http://upload.wikimedia.org/math/a/c/1/ac1ce7b36dbebe3adb8cca5790068816.png) 。
。
 純態與50%
純態與50%  純態組成,因此可見,不同的組合仍可得到同樣的混合態。
純態組成,因此可見,不同的組合仍可得到同樣的混合態。一般而言,完全隨機粒子束的
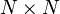 密度矩陣
密度矩陣  ,經過對角化之後,可以寫為[6]:186
,經過對角化之後,可以寫為[6]:186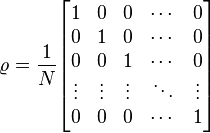 。
。
馮諾伊曼方程式[编辑]
薛丁格方程式描述純態怎樣隨著時間流逝而演化,馮諾伊曼方程式描述密度算符怎樣隨著時間流逝而演化。實際而言,這兩種方程式等價,因為它們彼此都可以推導出對方。假設,在時間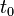 ,量子系統的密度算符為
,量子系統的密度算符為 ;
;
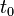 處於純態
處於純態 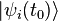 的機率是
的機率是 
假若不攪擾這量子系統,則機率
 跟時間無關。在時間
跟時間無關。在時間  ,純態
,純態 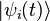 遵守含時薛丁格方程式
遵守含時薛丁格方程式 ,
,
 是約化普朗克常數,
是約化普朗克常數, 是哈密頓算符。
是哈密頓算符。所以,馮諾伊曼方程式表示為[7][8]
![\begin{align}i\hbar\frac{\partial}{\partial t}\rho(t) & =\sum_i w_i (H | \psi_i(t) \rangle\langle\psi_i(t)|- | \psi_i(t) \rangle\langle\psi_i(t)|H) \\
& =-[\rho,H] \\
\end{align}](http://upload.wikimedia.org/math/9/9/d/99d764b6f331ce6746529439e86627dc.png) ;
;
注意到只有當採用薛丁格繪景時(必須採用薛丁格繪景來計算密度算符)這方程式才成立,雖然這方程式看起來很像海森堡繪景的海森堡方程式,唯一差別是關鍵的正負號:
![\frac{dA^{(H)}}{dt}=-\ \frac{i}{\hbar}[A^{(H)},H]](http://upload.wikimedia.org/math/5/f/e/5fe6dd8d98bc9df70f217368be168aa5.png) ;
;
 是某種採用海森堡繪景的算符。
是某種採用海森堡繪景的算符。在海森堡繪景裏,密度算符與時間無關,正負號差別確使期望值
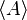 對於時間的導數會得到與薛丁格繪景相同的結果。[註 3]
對於時間的導數會得到與薛丁格繪景相同的結果。[註 3]假若哈密頓算符不含時,則可從馮諾伊曼方程式推導出
 。
。
馮諾伊曼熵[编辑]
在量子統計力學(quantum statistical mechanics)裏,馮諾伊曼熵(von Neumann entropy)是經典統計力學關於熵概念的延伸。對於密度矩陣為 的混合態,馮諾伊曼熵定義為[9]:301
的混合態,馮諾伊曼熵定義為[9]:301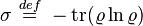 。
。
 是自伴算符,具有譜表示[6]:186-188
是自伴算符,具有譜表示[6]:186-188 ;
;
 是本徵值為
是本徵值為  的本徵態,所有
的本徵態,所有  形成一個規範正交基。
形成一個規範正交基。因此,可以將密度矩陣
 對角化,將馮諾伊曼熵更簡單地以對角化後的密度矩陣
對角化,將馮諾伊曼熵更簡單地以對角化後的密度矩陣  定義為
定義為 。
。
 又可以寫為
又可以寫為 。
。
在這裏,可以視每一個本徵值
 為處於本徵態
為處於本徵態  的機率。假若某事件的發生機率為零,則這事件不應貢獻出絲毫馮諾伊曼熵。從數學而言,以下極限為零:
的機率。假若某事件的發生機率為零,則這事件不應貢獻出絲毫馮諾伊曼熵。從數學而言,以下極限為零: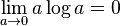 。
。
 。
。
 必定滿足
必定滿足 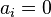 或
或 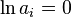 。
。完全隨機混合態的
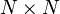 密度矩陣,其馮諾伊曼熵
密度矩陣,其馮諾伊曼熵  為
為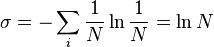 。
。
 ,而完全隨機混合態擁有最大的馮諾伊曼熵
,而完全隨機混合態擁有最大的馮諾伊曼熵  。
。每一次做投影測量,馮諾伊曼熵都會增加,永遠不會減少,但是,對於廣義測量(generalized measurement),馮諾伊曼熵可能會減少。[10][11]混合態的馮諾伊曼熵永遠不小於零。因此,純態可以通過投影測量改變為混合態,但是,非純態的混合態永遠無法通過投影測量改變為純態。投影測量這動作促成了一種基本不可逆性的對於密度算符的改變,如同波函數塌縮。實際而言,相當反直覺地,投影測量這動作抹除了複合系統的量子相干性。更詳盡內容,請參閱條目量子退相干。
一個量子系統的亞系統可以從混合態改變為純態,但是所附出的代價是其它部分的馮諾伊曼熵會增加,就好似將一個物體放進冰箱來降低其熵,冰箱熱交換器外的空氣會變暖,而所增加的熵會比物體所減少的熵更多。更詳盡內容,請參閱條目熱力學第二定律。

中观佛教和量子力学:对话的开始
独立于我们人类之外存在着这个巨大的世界,它在我们面前像是一个巨大的、永恒的谜团,但我们至少可以部分地检查它。
——阿尔伯特•爱因斯坦

一、导言
在上述引言中,代表着经典物理学传统顶峰的爱因斯坦,表达了他经常重申的对独立的、客观的世界的信仰。从一开始,量子力学就否定具有独立于测量的确定属性的客体,因此爱因斯坦总是发现他在反对自己协助创立的学科的基础。他最著名的异议——EPR悖论,引发了一场关于量子力学的基本原理和物理世界根本性质的旷日持久和精力旺盛的争论。多亏了约翰•贝尔在理论上和Aspect等人在实验上的出色工作,爱因斯坦的质问发展成了Abner Shimony称为“可诉诸实验的形而上学”的可能性。我们第一次能够用现代实验来真正解决重要的哲学问题。
既然发生在这场物理学基础的巨大风暴所吹起的尘埃已开始落定,我们可以更加全面地理解这一实验的哲学意义。我将不去关注实在论与量子力学的话题,这方面已经写了如此多的内容。尽管在量子力学中有反实在论的倾向,然而量子力学现在似乎与经适当修正的非还原论的实在论是可以相容的。我将关注量子力学中有关不完备性和非局域性的论题,而不是实在论,在前一方面已有可靠的理论和实验工作。这一工作令人兴奋之处在于,感谢由爱因斯坦所引发的质疑,我们可以通过实验来研究独立于量子力学方程的完备性和局域性的哲学问题。Aspect等人所发现的对贝尔不等式的实验否定,告诉我们的是关于世界的信息,而不仅仅是有关量子力学目前的方程。
伴随着物理学基础方面的变化,部分地是由于西藏佛教徒进入西方,西方对于中观佛教哲学内容的兴趣也在迅速增长。感谢许多学术成就,尤其是Jeffrey Hopkins和Robert Thurman的学术工作,具缘中观派——藏传佛教许多人认为是佛教思想的顶峰——的哲学原理现在正被用西方语言在从未预想过的细致程度上讨论着。尽管对中观的兴趣与日俱增,我仍然同意David Loy的估计:“考虑到中观的历史意义,西方对中观了解如此之少,真是一种思想的耻辱。”
本文试图利用中观研究的最近发展,并利用同一时期量子力学哲学基础上的澄清。我将把空性的核心教义和物理学中目前关于不完备性和非局域性的观点进行比较,然后把中观原理应用于对后者的理解。我要显示,在空性的中观概念与对贝尔不等式的实验否定和量子力学的基本原理之间存在紧密的联系。我希望这些比较和应用,能够激励在量子力学的哲学后果和关于解脱的古老教义的现代研究之间的对话。第2节讨论中观佛教中的空性,尤其是从具缘中观派的角度。通过严守当代西藏人关于具缘中观派的观点——它主要是依据宗喀巴的解释——我希望能避免目前关于早期中观的激烈争论。第3节简述贝尔不等式的哲学背景。第4节和第5节给出一个批判性实验的非技术的、然而是基本的讨论,它显示贝尔不等式的基本哲学内容。在此基础上,第6节作出比较和应用。第7节包括概述与结论。
最近的一些文章和专著,虽然其导向和焦点与本文不同,也都在现代物理学和佛教之间进行比较。为了尽量加强本文的可读性,我只要求读者具有最少的物理学背景知识,并给出中观理论的相当详尽的框架。
二、中观佛教的空性
佛教主要的兴趣在于将有情从无穷无尽的生死轮回(Sansara)的无明和烦恼中解脱出来。正如一名好的佛教医生一样,具缘中观派行者首先诊断出解脱的主要障碍——对固有存在的信念。然后他开出治疗这种瘟疫的处方——空性的哲学教义。在本节中我要简单描述具缘派治疗者眼中的病症和治疗方法。
具缘派声称,不管我们可能会主张什么样的思想立场,当我们检查我们在生存压力下的行为时,我们就会发现一种坚固的信念,相信客体和主体是根源其自身而存在的,是独立存在的,是像显现出来那样存在的;这些通过分析可以是发现的。(例如,假使一位学者的同行指责他剽窃抄袭,而他实际上是清白的,那么似乎是固有地存在的“我”就轮廓鲜明地站出来了。)独立于与其它客体关系或认知活动而存在着的客体,内在地非关系的客体,源自于自身存在的客体——这些对于除了深悟空性者之外的所有人来说都是实在的本质。这些描绘存在的不同方式,被交替地用来刻画具体的、独立的实在的原则,这种实在我们误认为是弥漫在我们生活中的。从这些哲学错误中产生了一连串的烦恼和局限,因为我们过高地估计了表面上非联系的和固有的存在客体(也包括了我们自己的心灵和心灵状态),将超出它们所包含的快乐和痛苦赋予它们。因此我们在烦恼的轮回中追求或逃避这些客体。
通过全面吸收终极真理——具缘中观派空性的教义,可以医治这种疾病。这种医治使我们转变成佛陀——彻底落实普遍慈悲教义的治疗者,主要是为了其它人的缘故已获得了解脱。具缘派通常使用三种力量逐渐增强的论证方式,来确立现象缺乏固有存在或现象空性,它们分别是:现象对原因和条件的依赖、整体与部分的关系、现象对心灵命名的依赖。建立这些依赖的方式,具缘派可以把缘起与缺乏孤立同一性等同起来(空性就是独立的和固有的存在的缺乏)。现象缺乏固有存在,或者说它们的空性蕴涵着缘起;反之亦然。为表达这些观念,我选取普通客体并分析之,它与经典的路线并非完全一致,但与之相容。在下面的段落中,我把在前一篇文章中的分析进行修改和扩展。
设想一棵苹果树生长在我的窗外,并且为小鸟、蜜蜂和主人所珍视。有什么能比这棵树更算是固有的存在?当然它依赖于许多原因和条件,如肥沃的土壤、气候和树的栽培与嫁接。但是这些形式的依赖,似乎都没有夺走树的独立存在。是的,我宣称拥有它,我的孩子攀爬它,但是这些联系的属性,对于其作为独立存在的真实本质似乎是相当外在的或者偶然的。
树由树干、树根、树枝、树叶和树皮等等组成。中观宗主张,树既非这些组成部分本身,也不是所有这些部分的总和。但是,尽管存在整体和部分的复杂的内在关系,普通人还是毫不怀疑,作为独立实体的树,可以在其组成部分和相互关系中找到。
当风儿轻轻吹动树叶时,我的狗所听的频率比我听到的要高,而享受花蜜的蜜蜂可以看到我所看不到的紫外线,但是却看不到这些花朵后来所变成的苹果的红色。我们的感官机能对树的表象当然有所贡献。但是我们仍然坚定地相信存在一棵“真正的”树——一棵独立的、非关系的、固有存在的实体,它是这些感觉属性的基础,并且可以解释我们共同具有的树的经验。让我们仔细检查这一“实在的原则”——这种固有的存在。
对于一个在一段给定时间内固有存在的客体,在这段时间的任何时段中都应当是同样内在存在的。客体在任何间隔(不管长短)都完全是其自身。按照佛教徒的观点,时间的瞬间被当作是原子式的,没有内在的转变或改变。时间的转变或时光之流就是瞬间的相继。
固有的存在是一种基本的属性,一定是不受任何限制地永远适合于对象全体的。既然对象在任何时刻是完全充实的和自足的,按照定义,该对象在任何时刻与在任何其它时刻的任何其它对象都没有内在的和基本的关系。因为内在存在的对象与其它时刻都没有基本的关系,而同时又延续了不止一个时刻,它必定是内在的无变化的,既不可能产生变化,也不可能接受变化。它是不受影响的和不能产生影响的,封闭在其永不改变的自性之中。任何内在存在的固体必定会凝固在永恒之中。
分析据认为是没有空间关系的对象,也可以进行类似的论证。它们在一个限定的空间范围中也一定是完全地和自足地存在,和与其它范围的相互作用无关的。正如基于时间的论证一样,这一不可避免的推理导致无法接受的孤立化和不变性。
对内在存在的非理性和根深蒂固的信念蕴涵了内在的无联系的实体。这种实体一定是自然的活力所无法触动的,因此不能变化,没有相互作用,也不能成为知识的对象。这种无联系的实体在我们流变的世界中不可能存在。虽然固有存在的客体确实不存在,习俗意义上的对象作为依存的和联系的客体则非常显著地存在着。空性并非虚无主义。存在着关于世俗意义上的实体和正确行为的有效知识。“我”作为对心灵和肉体的一种心智的命名,在世俗意义上确实存在。空性也不会落入常存的极端,因为对象缺乏内在的存在。对象既非作为不存在,也非作为内在的存在,而是作为缘起居于“中道”。
这一论证或解毒剂的力量,在很大程度上取决于我们是否同意诊断。如果我们提炼正常的经验,是否会发现人们信仰引诱其堕入生死轮回的独立存在?我们头脑中可能会有疑问,但具缘派在这一点上是坚定不移的。正如Hopkins所指出的那样“空性修证和生起领悟空性的智慧的关键,在于确认对象显现出它们似乎是存在于自身和由自身而存在的。”或者随后他说:“然而,具缘派回答道,‘固有存在’或者‘存在的自我模式’术语本身就暗示了独立性。”这种独立的、非联系的性质,我们误认为它赋予对象如此实体性和现实性,恰恰导致固有的存在自相矛盾和自我废弃。如果现象是依存性的,那么它们依赖于什么呢?
现象通过它们的相互联系而获得定义,并且依赖于这种联系。现象的本质是现象的联系性和依存性。内在的非联系性是一种自相矛盾的属性。虽然我们错误地假定固有的存在是表象的本质,但是中观派主张,正是一个对象缺乏固有的存在、它的空性、它的依存性,才使得现象可能产生并发挥功能。
那么现象为什么显现为固有存在呢?具缘中观派主张除了建立感觉知觉的细节之外,心灵会把将经验实体化和具体化,向我们呈现为主体和客体,它们错误地显现为固有的存在。换言之,固有的存在不过是概念的命名和增益——它从未存在过并且永远不会存在。然而我们却被深深地囚禁于不存在之中,囚禁于概念的命名和杜撰之中,这是我们本能地和被迫地所产生的思想的属性。从经验的模糊不清元素中,心灵杜撰出固有存在的客体,然后对此附加上贪恋和厌恶——这是生死轮回的两个脚镣。这种将经验实体化为独立存在的倾向,是我们与生俱来的无明的核心、痛苦的根源;对此可以用空性的教义驱除掉。
但是,虽然增益是独立存在客体错误显现的根源,心灵在其命名活动中与对象的(与内在的意义相反的)世俗意义上的存在也有关联。换句话说,伴随着心灵对内在存在非法的增益活动,它在对世俗意义上存在命名活动中合法地发挥其作用。心灵及其客体相互依赖的习俗存在确保了它们彼此的空性。因此,具缘中观派说,缘起——理性之王——在其最强有力的形式中是:“一切现象因为受到依存地增益,都没有固有的存在。”所有其它证明没有固有存在的推理都起源于这一理性之王,它可以彻底地克服常见和断见两种极端。
按照具缘派的观点,不仅没有通往独立于心灵的世界的道路,而且这样的一个世界根本就不存在。然而必须立刻申明,这种观点不是在其对手佛教唯识宗中可以找到的那种观念论。具缘派鲜明地强调对象外在于心灵,但是这些对象缺乏内在的或独立的存在。如果没有这种与心灵联系的外在客体,则无论是心灵还是客体都不会有世俗意义上的存在,因为它们彼此依存。不仅如此,任何心灵都没有内在的存在。如果它们内在地存在,则我们黑暗无明的心灵就不可能转变为光明的标志和佛陀的觉悟。
也许在中观阵营中最大的哲学竞争是具缘派和依自起派之间的竞争。近来由Hopkins和Thurman所撰写的最重要的专著全面地讨论了这种辩论。虽然论证经常是冗长和技术性的,我将简述依自起派的立场,并通过回答在这种辩论中可能产生的质疑来考虑一些批评的问题。依自起派同意具缘派的观点:在终极意义上,一切现象缺乏内在的存在,在最终的分析中找不到显现为内在存在的客体。但是,依自起派主张世俗意义上的对象确实内在地存在。他们在中观的两种真理的教义中作出他们的区分,宣称有两种互补的现象观:一种是终极的,认为一切都是空的,而另一种是世俗的,认为对象在日常生活的领域中具有存在、作用和效果。我们的普通生活和话语处于世俗真理的范围内,但是我们不幸地在世俗存在上增益内在的存在来玷污它。
依自起派论证说,如果客体在世俗意义上不是内在地存在的话,那么就无法解释客体特殊的作用以及我们所经验到的主体间的一致。我的树上悬挂的红色球体,是叫做苹果的能吃的果实,而非致命的毒药。心灵的命名、增益无法说明苹果的营养价值与毒药。按照依自起派的观点,需要一些独立的存在以说明这一特殊的性质,尽管最终一切现象都是空的。
具缘派对此立场进行了双重的否定:首先,以上的论证或者更加经典的论证显示内在存在的自我矛盾性。内在存在的不一致性在终极和世俗层次上都是平等的——仅仅为世俗层次保留内在的存在并不是将它恢复为一种有意义的原理。错误还是错误,不管是世俗意义上还是终极意义上。
其次,客体的空性、它的缘起性、以及它的各种关联和联系恰恰赋予了它功用和效能。苹果依赖于原因和条件、整体和部分、以及多方面的相互联系——独立存在的缺乏——确保了其世俗的存在、特殊性、以及我们主体间的一致性。将自相矛盾的内在存在赋予客体只会使得它们不能活动、永恒不变以及不能发挥作用。
最后,对于所有中观宗而言,空性是现象的终极真理。在内在存在的错误信仰之处,没有颁布任何更高的或更超越的原则。空性是无肯定的否定——仅仅现象中的独立存在。空性自身也是空的。
伴随着空性的原则,治疗的一个基本组成部分是普遍慈悲的修行。空性及其对我们彻底的相互依存和联系的确认蕴涵了普遍慈悲的教义。如果我们和每一种现象一样,是缘起的,那么痛苦和从痛苦中解脱出来都既不是孤立的也不是纯粹个人的事情。个人从轮回中解脱出来就不是目标。相反,认真的修行者发誓为了一切有情从轮回的无知和痛苦中解脱出来而勤苦修行。菩萨为了其它受苦的有情毫无保留地奉献自己。空性和慈悲之间有一种协同的关系——慈悲加深对空性的理解,而空性则为长养无限制的慈悲提供理智上的支持。中观宗以空性和慈悲的巨大支柱建立起佛陀的全部教义——这里表现了它的祝福。
三、贝尔不等式的哲学背景
本节中,我说明量子力学的争论是围绕着中观宗称之为内在存在的问题而进行的。把独立存在增益给现象的先天倾向,在经典物理学中发现了一个彻底的和量化的表达。另一方面,量子力学最革命的方面是其否认客体的某些属性具有独立的存在。这个侧面已经激发了许多批评和修正的尝试,尽管量子力学在实验和理论上已获得了意想不到的成功。最著名的批评就是由爱因斯坦所发起的,在最近对贝尔不等式的实验否定中达到了顶点。
爱因斯坦对量子力学的基础的伟大批评是从他在1927年的挑战开始的。批评的核心论文由爱因斯坦、波多尔斯基和罗森(EPR)于1935年撰写。尼尔斯•波尔迅速反驳了这篇文章,基本上大多数物理学家都同意他,这在后来成为量子力学的标准解释。但是这一科学的某些最重要的创始人如薛定鄂和德•布罗依都同意爱因斯坦。从关于量子力学的解释的论文的分量和争论的激烈程度上看,所有的关键问题都还没有彻底解决。
令人吃惊的是,尽管爱因斯坦是对量子力学进行批评的转折点,但直到最近几年学术界才澄清了爱因斯坦的批评和立场究竟是什么。EPR论文并没有包含爱因斯坦对这一问题上最清楚的表述。爱因斯坦的哲学立场最好的表达出自Dialectia。下面的引证出自Howard出色的翻译和评论:
如果要问,独立于量子理论的物理观念领域的特点是什么,那么下面的一切首先就会引起我们的注意:物理概念指涉一个真实的外部世界,即观念赋予号称独立于感知着的主体的“真实的存在”的事物上——这些事物的特点是被确定在一个时空连续统中。不仅如此,对于引入物理学的这种安排,最基本的似乎是:在一个特定的时间中,这些事物号称彼此相互独立,从而这些事物“处于空间不同的部分” 。没有这种有空间距离的事物彼此之间相互独立的假定——这种假定起源于日常思维,我们所熟悉的物理学思想就不可能。没有这种分离,就看不出物理学定律如何表达和检验。场论将这一原则推到极至,把彼此独立存在的基本元素定位于无限小的(四维)空间元素中,似乎是基本的定律对它们的要求。
对于相对论意义上独立的有空间距离的事物A和B而言,这种观点是有特点的:即在A上施加的外在影响对B没有直接的效果,这被称为定域作用的原则,只在场论中才有一致的应用。
定域作用的原则恰好表示光速是一切物理作用传播速度的上限。局域性在本文后面还要扮演一个角色。尽管在本节中没有讨论,所提到的“基本定律”是严格决定论的——相似的条件总是导致同样的结果,这个观点在量子力学中必须作重大修改。
对本文来说,比定域作用或决定论更为核心的是,“有空间距离的事物的存在,彼此之间相互独立,这种假定源自日常思维。”Howard称之为爱因斯坦的分离原则。在空间中分离并且没有物理学相互作用的客体,被看作是独立存在的,具有内在的、确定的属性。正是在这种基本存在的基础上,关系才得以建立;但是与关系者“彼此之间相互独立的存在”相比,关系的实在性较少,基础性较弱。当然,这种“源自日常思维的”对独立存在的信仰,中观宗毫不惊奇,因为他们说对内在存在的信仰是我们最深厚的与生俱来的无明。爱因斯坦也相信,彼此之间相互独立存在是对不同于习俗的客体作出一致定义所必须的个体化原则。这在中观宗的立场上看也是自然的,因为他们主张,缺乏独立存在才使得我们可能通过我们体现于命名或语言的习俗确保客体具有相对的存在——这正是爱因斯坦所想要避免的情形。(在具缘中观派中体现于语言中的习俗的重要性,及其与维特根斯坦的语言哲学的关系,有关的详细讨论,参见Thurman)
有人尝试将爱因斯坦的观点构建不同于标准量子力学的理论。通过假定局域性(没有任何通讯超过光速)和隐变量(目前还无法测量)的存在,局域隐变量理论尝试在量子领域重新恢复决定论和独立存在。为了检验这些理论,约翰•贝尔正是假定一切局域隐变量的核心,即局域性和独立存在,从而推导出预测这些理论在一组实验中相关结果的一个不等式。我下面要考察一个实验。(标准量子力学不遵循贝尔不等式。)实验否定了建立在这些听上去如此有道理假定上的贝尔不等式,我将要说明,这对我们的世界观产生了深远的影响。与此同时,实验与量子力学精确的一致强化了我们对于已确立的理论的信心。
这种“相互独立存在”,或爱因斯坦的分离性,在贝尔不等式的语境中拥有一种严格的(逻辑和数学的)表达形式。Howard已经显示爱因斯坦的彼此相互独立存在与完备性密切相关——一切可测量的属性在独立于测量的理论中得到全面说明的观点。我不对这些严格的结果进行评论,而是使用对上面解释的分离原则更加直觉地理解,并在下一节中将此观念应用于贝尔不等式的一个简单派生物中。
Paul Teller把这种对客体的孤立和独立存在的无所不在的信念称之为个别论,他确信这是我们在量子力学上遇到的许多困难的根源。他特别有效地指出,量子客体之间基本的联系性,以及要达到对量子力学的正确理解必须抛弃个别论。D.Howard1985年的论文也包含了类似的观点。
我认为,彼此之间独立存在的观念——Howard称之为爱因斯坦的分离性、Teller称之为个别论——以及完备性的观念,在中观宗确定的内在存在中都是基本的成分。内在存在及其否定是比科学哲学所关注的更加宽广的一组问题。但是在现代科学哲学家和中观宗行者共同关注的领域中,他们所讨论的完全是同一个问题,不管你称之为内在的存在、分离性、完备性或者个别论。以下两节讨论实验和量子力学是如何否定内在存在的。
四、相关性实验
本节包含一个有关检验量子力学概念基础实验的非技术的讨论。虽然描述是经过调整的,但它忠于实验的物理学精神。感谢David Mermin,我们可以不受物理学和数学的技术限制而严格地表述贝尔不等式的哲学精神。在本节及下节中,我把他的著作中的内容抽提出来并予以扩展。
这个实验包含了三个主要成分。图1显示一个产生相关光子对的光子源置于在两个同样的偏振检测器中间,成一直线。(相关意味着什么下面就清楚了。现在我们可以说一开始在一起的光子之间即使在分开之后也能保持某种确定的关系。)相关光子对同时由光子源发射,每一个朝向一个偏振检测器。
贝尔分析的一个魅力是,它不需要描述或理解偏振性或检测器的物理性质。关于实验装置,我们所需要知道的是,每一次光子进入检测器都会记录下+或-。虽然如此,如果知道这点就会更好:即每一个检测器像偏振太阳镜一样作用,只会透过落到其上的某些光线。如果光子通过,检测器记录+,要是没通过,就记录-。正如偏振太阳镜一样,偏振检测器的效果随其围绕光子运行的路线旋转而改变。每一个检测器可以在A、B、C位置之间迅速切换,从光子源看过去方向依次相差120度。(见图1)一次只能有一个切换。任何一次切换每一个光子落在检测器上都只能记录+或-。
实验以下述方式进行:相关光子对同时送往每一个检测器。在光子达到检测器之前每一个旋钮独立地和随机地重新调整。每一个偏振检测器独立和随机地调整意味着9种可能的组合将会平等地发生。它们分别是A-A、A-B、A-C、B-A、B-B、B-C、C-A、C-B、C-C,其中第一个字母代表左边检测器的旋钮,第二个字母代表右边的旋钮(例如B-C表示左边检测器定于B,而右边检测器定于C)。数量极多的光子对送往检测器,反应被记录下来。任何一次我们只可以测量到如下的检测器反应:++、+-、-+、和--;其中例如+-意味着左边光子通过了检测器而右边则没通过。这些就是实验的主要思想。
与实际的实验一致,把距离和旋钮确定的准确时间安排成在旋钮确定之后,信号以光速运行传播也无法从左边检测器在右边被检测之前到达检测器。既然光速被假定为任何影响或信息传播速度的上限,这就保证了在不同检测器上旋钮确定和测量之间不可能存在通讯,一个检测器的旋钮确定和测量不会对另一个检测器旋钮确定和测量产生影响。例如,假设检测器相距一光年之遥,检测器重新随机确定1秒之后进行测量。检测器重新确定在一边,测量的事件发生在另一边,依照相对论在四维时空中具有类空(space-like)分离性,在类空分离的事件之间通讯行为不可能发生。假定光速是物质作用或通讯传播速度的上限,这是对局域隐变量理论和量子力学同样适用的普遍假定。这得到了理论和实验的压倒性支持。正如下面将清楚显示的那样,排除两次测量或旋钮确定之间的物理关联或“共谋”的能力在解释中是至关重要的。
五、局域隐变量解释:贝尔不等式
局域隐变量理论在物理实在论中有其根源——对应于一个独立于观察者的世界,一个具有确定的、在测量之外完全可以说明的属性的世界。这自然导致对于一个完备性理论的要求,即一个系统所有可以测量的属性在独立于测量的理论中可以得到完全的说明。或者用EPR的使用可以保证系统的属性独立于类空分离事件的局域性原则,来建立物理实在的要素。
在眼下的事例中,完备性和局域性允许我们假定偏振性(它决定一个光子是否可以通过特定位置上的检测器,检测器是否记录+或-),对于光子是内在或固有的,是独立于类空分离的旋钮确定或事件的。换言之,我们是在体现爱因斯坦的要求“空间上有距离的事物之间的相互独立存在。”在一边的一个光子按假定具有一种确定的偏振性,它是先于并独立于在另一边的测量的。假定光子的这种内在属性独立于特定的旋钮确定和远处的测量结果,这自然得我们对此不加思考;但这种“起源于日常思维的”似乎清白无辜的假定,按照爱因斯坦的观点,正是局域隐变量理论的核心。
在附录中,我提出了贝尔不等式的一个简单形式的非技术的变种,它仅仅假定了局域性和相互独立存在(确定的偏振性独立于测量)。虽然这个变种是严格的,它只要求基本的高中数学。这种简单形式的贝尔不等式预测至少1/3的光子应该记录为同样的符号,如果在两个检测器中随机设定的旋钮是不同的话。测量的结果准确地显示只有1/4的光子记录了同样的符号,当旋钮不同的时候。
但是我们如何来理解实验对建立在这种似乎“不证自明”假定基础上的不等式的破坏呢?作为准备的尝试,我们可能会说,当对相关光子对中第一个光子进行测量时,第二个光子迅速变为相关的状态,从而改正了统计结果(1/4)。但是在实验中,时间的安排使得第二个光子的测量与第一个光子的测量之间具有一种类空的分离,因此有关什么是“合适的相关状态”的信息传播一定比光速更快——这在任何人看来都是严重的问题。问题甚至更为严重,因为正如我在附录中所显示的那样,假定局域性和独立存在就蕴涵着第二个光子已经具有了完全确定的、与第一个光子同样的偏振状态。在这两个假定下,光子不能只是简单地像变色龙一样在最后时刻改变其偏振状态,从而改正统计结果。局域性或独立存在(或者二者)在自然中一定遭到了破坏。
在下一节中,我检查更加精致的相关光子模型,但是结论仍然成立。在光子之间存在着神秘的关联性或非局域性。它们的表现不像分离的实体而更像相互联系的整体——但是我们在每一个检测器上测量粒子般的实体。正如我在下一节中所强调的,我们本能地把光子实体化为具有“相互间独立存在的”完全确定的实体。这使得要从我们在如此彻底投入了独立存在信念的世界的经验中建立一个相关光子的模型根本不可能。虽然如此,在下一节中,我尝试用空性的观点来详细阐明我们对这一神秘现象的理解。
这里必须强调两点:首先,对贝尔不等式的否定并不依赖于量子理论,虽然对这种实验的考虑当然是由量子理论的特殊性质所激发的。其次,这些结果并非局限于亚—微观领域,因为检测器分离达13米之远。这里讨论的量子效应通常并不在宏观领域中出现,但是在原则上和在实际上,它们并非局限于微观世界中。
对于局域隐变量理论及其局域性和完备性的假定,量子客体独立于类空分离的事件具有一个完全确定的性质,换句话说,它们内在地存在着。实验对贝尔不等式的否定要求对这些假定放宽一个或全部放宽。正如我下面所强调的,放宽这些假定其中之一就是承认量子客体具有根本的相关性或相对的相关性——这是对它们空性或缺乏内在存在的断言。
六、比较与应用
中观宗和实验对贝尔不等式的破坏二者,都向我们最珍视的实在性原则——独立的或者内在的存在——提出了尖锐的挑战。但是物理学只研究物质领域,而中观则分析一切人类经验;所以比较能走多远呢?不仅如此,虽然局域隐变量理论及其完备性和局域性的假定是站不住脚的,但就实验对贝尔不等式否定的后果并未达到完全的一致意见。对于量子力学的哲学意义也还有许多争论。在我们对贝尔不等式破坏的理解这个阶段上,以及我们目前对量子力学本身的理解水平,我们可以有理由肯定什么呢?在本节中,我将部分地回答这些问题,强调这些事实依赖于我们目前对物理学的理解,开始将中观的空性教义应用于对贝尔不等式和量子力学的解释,并将其与由Paul Teller和其他人发展的量子力学的哲学结合在一起。
在接下来的段落中,我只提供反对决定论的局域隐变量的例子,正如贝尔在他1964年的分析中所做的那样。在这些理论中,假定光子离开光子源之后偏振性具有一种确定值。例如,附录表1中第一列显示光子8种可能的偏振性确定状态,光子完全决定了检测器对于一个给定的位置反应。在稍后的工作中,贝尔和其他人分析了更加普遍的局域随机隐变量理论。这些同样被实验所排除的理论,只给出了检测器反应的这样的概率,它们依赖于光子和检测器位置的一些更加普遍的状态。光子不是被看作携带一种偏振性的确定状态;所以我们将我们的注意力转移到检测器反应的概率上来。现在完备性和局域性的概念变得更加微妙了,但是感谢Jarret和Shimony,我们准确地知道在这些局域随机隐变量理论中独立性的假定如何进入了贝尔不等式。假定了三种型式的独立性:
1、一侧检测器反应的概率独立于另一侧开关的位置。
2、光子源发出的概率的统计混合独立于两侧检测器的开关位置。
3、一侧检测器反应的概率独立于另一侧检测器的反应。
分析显示,局域性只要求第一种和第二种独立性,这同样也为量子力学理论所遵循。但是结果独立性(第三种)却不为量子力学所遵循。考虑到局域性的压倒性证据,结果独立性是一种自然和量子力学似乎都破坏的假定。要将检测器反应的概率或者一侧结果的概率隔离出来,并认为它与另一侧的结果分离开来是不可能的,即使在两侧的测量之间不可能有物理或信息的关联。这对大多数人来说是神秘的。按照中观所激发的评论,这种神秘观可能会有所减弱。
尽管在量子力学中,光子是最瞬时的实体,从幽灵般的概率中喷发出来接受测量,我们还是倾向于将它们当作沿着确定的轨迹在空时中旅行的具体的实体。我们太过经常地隐含地假定,它们是完备和自足的,独立于间隔的状况和事件。例如在教室、实验室、或者在目前这篇文章中,我们差不多总是这样来谈论贝尔实验:“两个相互关联的光子被送往相反的方向。”理智上我们完全知道,相互关联的光不可能严格地在这种分离的意义上来考虑,但是我们几乎总是陷入这种思维习惯中。我们经常实用地辩护说,这会使得特殊的应用更加容易。但是即使是关于局域性的讨论,也经常隐含地假定一个完全确定的粒子般的实体,其在轨迹上瞬间的位置与另一个事件是或不是类空(space-like)分离的。(施加局域性的限制并不一定牵涉这一概念上的谬误。)换言之,我们通过将光看成是一种在完全确定的轨迹上运行的粒子般的光子,积习难改地将内在的、非关系的存在增益给光。这种与生俱来的倾向就是Teller所说的“个别论”的毛病。这种思维习惯如此强大,以至于它甚至也体现在John Weller经常重复的唠唠叨叨命令中:“以今天话说,波尔观点(和量子理论的核心内容)可以归纳为一个单一的、简单的语句‘任何一个现象,除非是一个被观察到的现象,否则就不是一个现象。’”虽然光除非被观察到否则不是一个光子,我们通常还是把它看成是一种独立存在着的实体,具有完全独立于遥远的事件和结果的属性。
虽然是我们器官活动正常通常模式的剧烈颠倒,中观断言现象的最高真理,其最基本的性质,是其内在的依存性和彼此的关联性。现象的基本性质是其关联和联系,而不是其孤立的同一性。通常的思维习惯承认对象的联系,例如相互联系,但是认为这些属性对于光的基本属性来说是偶然的。或者像Teller可能会说的那样,某些量子属性(例如相关光的性质)是内在联系的——其基本联系不会超越于其非联系的属性。Teller不会从全面的角度来考虑个别性与内在联系,即不会像中观应用类似概念——内在的存在与空性——那样。在他思维的这个阶段,他只把他的原则应用于解释科学哲学问题,而没有确定其可应用的范围。
实验显示了,相关性对于光来说在最基本的意义上是内在的——一侧检测器测量的结果与在另一侧发现的结果精密相连。在现象的终极真理是内在存在的空性、其依存性和相关性这一意义上,我们不能也不应该用试图通过各种(超出光之外的或其它的)联系使内在存在的实体发生关系来寻求对这些相关属性的解释。换言之,总是这么说是令人厌烦的:“本质上联系的实体在一边,它在测量时被命名为‘光子’,它与另一边的关系性实体的联系是如此本质性的,它们必须被整体性地考虑。”但是量子的形式化及其叠加的原则在数学上告诉我们的正是这种类似的内容,尽管我们在将其应用于我们正常的实体化或个别化思维方式时会感到困难,这种思维不加反思地将现象增益为内在的存在。
如果局域性在未来的物理学中需要修改的话,那么这对物理学将是极端重要的,但是与我们今天的讨论没有直接的关系。因为那时说检测器的反应是一个依赖性相关事件仍然是正确的,它将会是以类空分离的事件为条件的或者说瞬间依赖的。这种对类空分离事件的依存性将会是对其独立存在的断然否定。内在的存在,至少在贝尔类型的实验中,在未来的物理学中是不可能复辟的。
尽管量子力学在过去60年中取得了意想不到的成功,包括最近令人震惊的强、弱相互作用和电磁作用的统一,量子力学目前的形式可能会比实验对贝尔不等式的否定还要短暂。即使如此,简要地描述量子力学最基本的概念原理并将其与中观的分析联系起来还是值得的。
量子力学的哥本哈根标准解释有两个紧密联系的核心原理。首先,量子对象不具有客观的或者具体空时的存在,即不具有独立于整个测量状态的完全确定的可测量的属性。永远必须要在进行测量的具体实验安排的背景下才能考虑对象。在上述实验中,一侧检测器的反应虽然与另一侧检测器的反应是类空分离的,必须要与它整合起来考虑。未经测量的对象,独立于其被观察的确切实验状态的对象,根本就不存在一个确定的客观状态。观测仪器和被观测对象是一个按照量子力学所涉及的无形整体或系统的互相补充的组成部分。按照波尔的观点:“孤立的物质粒子是一种抽象,只有通过其与其它系统的相互作用才能确定并观察其属性。”在中观中类似的思想运动是确立所有对象都缺乏独立的存在。
在上述的实验中,按照量子力学的标准观点,光子并不具有完全确定或外在的性质(偏振性组合如+-+或者-+-),即不具备先于或者独立于现实的测量事件的性质。在测量事件前,对象只有的抽象“存在”,即只有作为由波函数所描述的相互贯通的概率或者相关的潜在可能性,只有包含了有关量子体系的所有可能知识的量子力学的数学结构。虽然波函数是我们所能获得的有关体系的最多的知识,但是它并不涉及到任何具体存在于空时中的物质的、客观的实体。相反,叠加原则是内在的联系在数学上的一种表现。虽然在检测器的反应之间不存在任何物理的或信息的联系,一侧检测器检测的可能性依赖于另一侧检测器的反应:内在的联系具有可测量的后果。
即使在对量子力学的各种解释之间对有关量子测量过程的细节存在着争论,许多人(如在哥本哈根解释中)都断言:测量是量子事件向宏观世界中的事件的一次不可逆地放大。因此看上去具缘中观强调对存在的增益与量子力学是有矛盾的。当然,总是可以像许多人争辩的那样,说一切科学都是一种心灵构造的世界,它是从人与自然之间复杂的相互作用中产生出来的;但这不是现在的关键问题。量子力学根本不像中观派那样把意识置于核心位置。这种明显的分歧可以通过欣赏中观的认识论和形而上学观点的区别而得以缓和。认识论对于为什么对象表现出独立存在的解释是用增益的术语给出的,而习俗对象被理解为由心灵命名的;但是形而上学的真理却是:即使抛开心灵的作用,对象也是依存地相互关联的。对佛陀而言,世界被真实地看作是空的、依存地相互关联的,并且不存在施加于现象之上的独立的增益活动。事实上,传统宣称佛陀甚至连一个可以将名义上的存在增益于对象的概念意识都没有,尽管佛陀所感知的一切只是名义上的存在。
这种量子力学的非意识解释的一位著名捍卫者,John Wheeler也清楚地理解心灵增益内在存在或(Teller可能会说的)个别化的倾向。Wheeler说,“我们称为实在的内容包含了几个观察的标竿,我们用一种精致的想象和理论的人为构造物填充于其中。尽管在日常的环境中说世界独立于我们而‘外在地’存在是有用的,但这种观点是再也站不住脚的。在这是一个‘共同参与的宇宙’说法中有一种奇异的感觉。”
这牵涉到哥本哈根解释的第二个原理:对象由测量活动本身带到了客观的存在。对象只有通过测量活动才能变成空时现象。或者,如Wheeler所说:“除非是被观察的现象,没有一个基本的现象是现象。”在中观的语言中,实体仅作为缘起的种属而存在。在中观中发现的空性与缘起的亲密关系,与量子力学中发现的很相像,解释中的这两个主要原则总是保持紧密相连。
七、概括与结论
量子力学60年来在权力、可应用性和优雅方面稳步地增长和加强。从20年代末和30年代初波尔、海森堡、波恩和其它人发展量子力学的哥本哈根解释以来,其哲学原理只经受了适度的修正。尽管如此,关于量子力学的意义仍然存在热烈的辩论,其中许多由这里评述的最近贝尔的分析所加强。量子力学缺乏合适的哲学框架确实是量子革命如此缓慢和痛苦的主要原因之一。我已尝试表明,对中观关于空性观点的同情理解可以帮助消化量子力学的意义。像Teller一样,我主张将我们的哲学立场从个别论或对内在存在的信念转移到基本的关系性,而不是修改量子力学的数学结构。
一方面中观可能对理解量子力学有所帮助,同时量子力学也可以帮助理解中观。如果这种古代的教义要征服现代人,它需要更多的当代例证,而不是“龟毛的外套”或者将绳子误认为蛇。量子力学可以提供强有力的例证来说明中观的某些侧面。它也可以复活例如具缘中观派和依自起派古代的争论,后者主张在习俗意义上有内在的存在,这种立场在实验对贝尔不等式的否定面前更加难以坚持。
然而,目前这篇文章决非要通过物理学来证明中观佛教的有效性。使用科学证明或者否定各种宗教或世界观的主张有一个命运不济的漫长历史。撮合一种世界观与科学婚姻的尝试注定会过时。相反,我所做的是尝试理解重要的和经实验证实的哲学论断,使得关于某些量子属性缺乏独立存在的个别化理论独立化,并将其与中观的空性原理结合起来。
虽然许多哲学体系可以与实验对贝尔不等式的否定结合起来,我主张(中观的关键概念)空性,谈论量子力学的核心问题具有独一无二的直接性和力量。我已尝试应用空性来理解实验。然后我给出量子力学的标准观点,并因此建立与中观进一步的联系。我希望用这种方式去获得对古代解脱哲学和现代物理科学结果的一种更深层次的欣赏。考虑到科学技术世界观的压倒性主导地位,目前形式的比较工作当然是中肯的,如果它能避免将中观或任何其它类似的思想主体部分还原为科学的一个分支的罪恶的话。
附录:贝尔不等式的非技术性推导
假定上述包括到第五节前两段的讨论,我们可以推导出贝尔不等式的一个简单形式。现在我给出一个非技术的推导,它只需要基本的高中数学。
为方便起见,以第四节中描述的方式所收集的数据可以分为两种情形:情形1,两个检测器具有相同的开关设置,情形2,开关设置不同。下面逐一探讨。
情形1:两个检测器具有相同的开关设置。
现在数据是在开关设置为A-A,B-B,C-C的情形下收集的。这是EPR1935年在挑战量子力学的论文中所考虑的实验的基本精神,尽管那时只是一个思想实验而已。其数据可以简单概括如下:
1、两个检测器总是记录到以同样的概率随机产生的相同记号++和--。
2、+-和-+从不产生。
首先,必须确立两个关键的事实:在情形1中,对于三个检测器设置A-A、B-B、C-C中的任意一个,测量总是产生“+”“+”或“-”“-”而从不产生“+”“-”或“-”“+”。从这一点,我们可以推断出第一个关键事实:光子对的每一个成员在一个选定的方向上一定有相同的极性。如果在选定的方向上极性不相同,则可能会测量到+-或-+的结果,和情形1的结果相冲突。通过回忆一侧的开关设置与测量和另一侧的之间具有类空分离来确立第二个关键事实。它们之间不可能发生通讯,右侧粒子和检测器无法知道左侧检测器的位置和测量。因此我们可以选择沿着B或C测量右侧光子的极性,不会有充足时间将此信息通过任何方式传回给左侧光子来影响左侧的测量。例如说,我们用设于A的左侧检测器测量得+,设于B的右侧检测器测量得-。依靠着一对光子在一个给定的方向上观察到相同的极性,我们实际上测量了右侧光子的2个成分(沿A+和沿B-)。当然,这还利用了完备性或左右两侧光子存在彼此相互独立的假定。
我们同样还可以选择沿着C测量右侧光子,从而获得沿着A和C两个方向的两个值。这样我们推断右侧光子在A、B、C三个方向上一定同时具有完全特殊的极性,不管开关的设置如何。既然论证对于左侧和右侧来说是对称的,这就确立了第二个关键事实:两个粒子一定对于三个可能位置中任何一个都具有完全特定的极性。这两个关键的事实联系起来意味着,极性设置在三个方向上完全是特定的,并且它们与每一个光子对同一。情形1的数据连同局域性、彼此相互独立存在的假定,以及归纳推理的使用要求这一结论。
在前述的分析中,标准的推广是从以相同开关设置测量相同极性光子对的案例到不同开关设置的案例。既然一侧的测量或者检测器不可能影响到另一侧的测量或者检测器,我们基于彼此相互独立存在推断所有光子对在三个方向上一定具有相同的极性,不管其开关设置如何。
使用一个简单的符号来列举极性可能的不同种类,例如+--代表了一个光子在方向A上测量极性的结果是+(通过),在方向B上-(没通过),方向C上-;而+-+代表一个光子在方向A上+,方向B上-,方向C上+。有八种可能的极性组合:+++,++-,+-+,-++,---,--+,-+-,和+--。现在该考察开关设置不同时所收集的数据。
情形2:两个检测器具有不同开关设置
考虑一下开关设置为A-B,A-C,B-A,B-C,C-A,和C-B的情形。约翰•贝尔1964年的显赫成就是EPR思想实验的推广。正如下面所显示的那样,通过考虑开关设置不同的情形,实验可以直接与局域性隐变量理论对质。情形2的数据如下:
1:在1/4时间中检测器记录到以相同几率随机产生的相同符号++和--。
2:在3/4时间中检测器记录到以相同几率随机产生的不同符号+-和-+。
情形1和2的数据的独特型式起源于成对光子间相关性——一侧检测器测量的结果相关于,或者说关联到另一侧检测器检测的结果。
表1列举了情形2的测量的可能性。8行对应于可能的极性组合。6列对应于可能的开关组合。表中每一条目或是“同”或是“异”,表示条目的极性组合对于特定开关设置时,光子对产生相同或不同的测量结果。例如,表中下划线的条目表示当极性组合为+-+而开关设置为A-B时,两个光子被检测为不同的记号(左侧光子在A方向上为+,右侧光子在B方向上为-)。表1显示除了+++和---的极性组合外,总是有2个开关组合产生相同的结果,4个组合产生不同的结果。
相关表1
A-B A-C B-C B-A C-A C-B
极性
+++ 同 同 同 同 同 同
++- 同 异 异 同 异 异
+-+ 异 同 异 异 同 异
-++ 异 异 同 异 异 同
--- 同 同 同 同 同 同
--+ 同 异 异 同 异 异
-+- 异 同 异 异 同 异
+-- 异 异 同 异 异 同
既然开关是独立和随机地设置的,我们知道对于一个给定的极性,6种开关组合发生的几率是相同的。暂时假定我们有一大群相同的光子——每一种极性组合都有相同的可能性。换句话说,在一个相同的样本中光子+--的可能性会像+++或者任何别的极性一样。按照这中假定,表中的每一个条目都具有相同的统计权重。表中有同样数量的“同”和“异”,因此如果测量这一相同样本的大量光子,有一半时间会产生同样的测量结果。
由于很快就会清楚的原因,接下来假定一个不一致的样本,其中的光子中没有+++或者---的极性,但是其它的极性表现是相同的。通过这种方式,我们去除那些对于所有开关设置总是产生相同结果的极性。现在对于所有剩余的极性有2个“相同”和4个“不同”,因此具有这些极性的光子(我们假定的不一致的样本)将总是只能记录到1/3的同样结果。对表1的思考显示任何极性的组合都将会产生至少1/3的相同的测量结果。换句话说,假定在一个测量样本的任意选择极性的混合,一定至少产生1/3的相同测量结果。
以上简单的记数练习显示(假定局域性和存在是相互独立的)至少1/3的光子应该记录到相同的符号。这是一个贝尔不等式的简化形式。另一方面,实验的结果是1/4——这正是标准量子力学所预言的结果。
上述结果如此重要而又优雅简洁,值得总结概括:情形1的数据显示当开关设置相同时(A-A,B-B,C-C),检测器的反应总是相同的。因为开关设置的时间安排,在局域性和相互独立存在的假定下,极性完全是特定的和等同于相关光子对的每一个成员。表列举了8种可能的极性及其对于6种不同的开关设置所产生的测量结果。它显示当开关设置不同时,没有任何极性组合所产生的测量结果中相同记号占检测器反应的比例低于1/3的;然而实验结果是1/4。实验对贝尔不等式的严格否定,上述记数的一种推广,迫使我们抛弃局域性隐变量理论。
在这篇论文的主体部分,尤其是在第5节和6节,我尝试了说明实验对于违反贝尔不等式的哲学和物理学意义。
作者:维克多•曼斯菲尔德
(原美国Colgate大学物理学和天文学教授)
译自International Philosophy Quarterly Vol. XXIX. No.4 Issue No. 116 (December 1989) PP371-387
佛教与科学


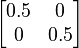




 或下旋
或下旋  ,
,



No comments:
Post a Comment