光的故事:發現第二個愛因斯坦: - 第 20 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=9867386558
鄭天吉吉,姚福燕 - 2012 - Education
既然我們已經知道夸克必須具有分數電荷,而其他任何類型的粒子都不具有分數電荷,那麼根據分數電荷,可以很容易地辨認出一個自由夸克。不過,迄今為止還從未發現 ...
https://books.google.com.hk/books?isbn=9867386558
鄭天吉吉,姚福燕 - 2012 - Education
既然我們已經知道夸克必須具有分數電荷,而其他任何類型的粒子都不具有分數電荷,小偷也要懂牛頓:趣味物理現象: - 第 64 頁 - Google 圖書結果
https://books.google.com.hk/books?isbn=9866941388
崔相壹博士 - 2013 - Education
1897年,英國人湯姆遜(1856年~1940年)在倫琴真空管中產生的部分射線中發現了一些帶有負電荷的微粒(後來這些粒子被稱為「電子」electron)。湯姆遜在1897年4 ...
https://books.google.com.hk/books?isbn=9866941388
崔相壹博士 - 2013 - Education
1897年,英國人湯姆遜(1856年~1940年)在倫琴真空管中產生的部分射線中發現了一些帶有負電荷的微粒(後來這些粒子被稱為「電子」electron)。湯姆遜在1897年4 ...OLED: 有機電激發光材料與元件 - 第 270 頁 - Google 圖書結果
電的認識
home.phy.ntnu.edu.tw/~eureka/contents/elementary/chap%206/6-1.htm
物體經摩擦起電後,稱為帶有電荷(charge)。由實驗中發現有些物體上的電荷可以自由移動,稱為導體,例如銅、鋁、……等;反之,另有些物體上的電荷則不能移動,稱 ...
home.phy.ntnu.edu.tw/~eureka/contents/elementary/chap%206/6-1.htm
物體經摩擦起電後,稱為帶有電荷(charge)。由實驗中發現有些物體上的電荷可以自由移動,稱為導體,例如銅、鋁、……等;反之,另有些物體上的電荷則不能移動,稱 ...網頁
www.phyworld.idv.tw/BA_CHE/CH2/2-1_EX_2_ANS.htm
下列關於原子核的敘述,何者正確? (1)原子核只占整個原子很小的一部分體積(2)原子核帶著原子中所有正電荷(3)原子的大部分質量集中在原子核(A)僅(1) (B)僅(2) ...
www.phyworld.idv.tw/BA_CHE/CH2/2-1_EX_2_ANS.htm
下列關於原子核的敘述,何者正確? (1)原子核只占整個原子很小的一部分體積(2)http://www.msckobe.com/links/yang.htm
二十世纪理论物理学的主旋律【杨振宁】
各位贵宾,各位同学,我非常高兴有这个机会跟人么多同学谈一谈,二十世纪理论物理学 的一些发展,从任何一个眼光来讲,二十世纪都是一个非常有大进步的一个时期。自人类远 祖发现火以来,在二十世纪人类第一次发现了第二种能源,比火要强的核能,另外人类学会 了控制电子的行动,从而创造出半导体,引导出来计算机,引导出来通讯工程,大大提升了 人类的生产力。人类发现了研究极小结构的方法,从而发现了双螺旋的结构,引导出来生物 工程技术。人类首次能够离开了地球的引力场,登上了月球。这种种世纪里面的大事,都与 物理学的发展有密切的关系,可是刚才几分钟我所讲的都是比较跟实际生活有关系的一些发 展。而物理学上的也有长足的发展,这些长足的发展是的我们对于时间、空间、运动、能量、 力量这些最基本,最原始的观念有了更深入的了解。而如果你想一下子的话,刚才我所讲的 跟应用比较有关系的一些发展,它们其实都是基于这些原始的、基本的观念上的革命才能造 成的。最简单的比如说是计算机,如果没有半导体的发展,不可能有今天的计算机工业;如 果没有量子力学的发展,不可能有半导体的产生。而量子力学的发现,当然就使得我们对于 时间、空间、运动、能量、力量都有了更深入的了解。所以如果我们说二十世纪的整个的发 展是奠基在基本理论物理学的发展上,这个不是言之过火的一句话。
我今天预备跟大家提的就是好像是交响乐里头的主题旋律themetic melody。那么如下我 们想一下二十世纪的物理学里头有些什么themetic melody呢?那是量子化、对称跟相位因 子,这三个观念的改变、演进、纠缠在一起,造成了二十世纪理论物理的主体发展。
第一项是量子化,量子化是在1900年二十世纪开始的时候,由一个叫做Marx planck的德 国人所写的一篇文章中引导出来的。这个你们也许看不清楚,这是我从他的那篇文章的第一 页上面复印出来的。你如果看这篇文章后来的这一页的话,到这个地方,底下有一个你们也 许看不清楚,是“B=6.885×10的负二十七次方”尔格秒。这是第一次人类引进了这么一个 常数,这个常数今天叫做Planck's Constant(普朗克常数),而你如果看今天非常准确的 这个常数的值跟一百多年以前普朗克所决定的这个值只差4%。普朗克当时是非常大胆地写 了这么一篇文章,他说这个光的吸收跟发射不是一个连续的,在那个以前大家认为光法出来 或者吸收进来是一个连续的步骤,他说不是,是一阵子一阵子的,每一阵子叫做一个量子。 他这个文章发表了以后他越想越觉得恐怕不对,所以他变得非常的胆怯,如果你去看他以后 几年的文章的话,你就发现他一步一步在向后撤退。为什么他要撤退呢?因为他想要把他非 常大胆的地写出来这片文章跟传统的物理学放在一起,他觉得不能够互相相容。可是1905年, 26岁的爱因斯坦写了一篇文章,他不但没有撤退,他向前更进了一步,他的这个大胆当时是 非常惊人的,这一点也是爱因斯坦一生的工作一个特点。他最会抓住非常微妙的,可是当时 是非常重要的领域,向前大大地迈一步。他们的工作又过了几年,由当时另外一个的叫尼尔 斯·玻尔的年轻人在1913年又迈了一步,把普朗克的观念和常数引到原子构造这一方向。我 想大家念过高中物理的话,可能都听说过或者了解到一些玻尔当时的想法,玻尔的这个工作 出来了以后,因为它跟实验有很多吻合的地方,所以震惊了整个物学界。他当初是讲氢原子, 可是把它运用到比较复杂的问题时,比如说是氦原子,有两个电子的,就立刻出了一个非常 困难的问题。这个困难的问题最初以为是一个数学的问题,可是研究了很多年以后发现不只 是数学的问题,虽然数学的问题并没有严密的解,可是可以近似地解,这个近似的解跟实验 的结果差得很远。在那个以后有十几年的功夫,是物理学初在一个非常紊乱的状态,在那个 时候的工作者是有非常稀奇的心理状态,有时候猜,猜出来一个结果跟实验吻合,于是大喜 若狂,可是过两天想一想觉得完全不对,又是非常沮丧。所以在前些年,一位有名的科学史 专家叫亚伯拉罕·派斯(ABRAHAM PAIS),他写了一本书(Niels Bohr's Times, In Physics, Philosophy, and Polity)讨论那个时候的发展。那么他引用了查尔斯·狄更斯在 《双城记》里边所讲的,说是“It was the spring of hope ,It was the winter of despair”,那是有希望的春日,那是无前途的冬夜,这个确实是描述了那个以后十几年物 理学家的心态。又譬如玻尔给卢瑟福,卢瑟福当时是世界最重要的实验物理学家,玻尔可以 说是他的博士后。玻尔在1918年给卢瑟福的一封信说,现在我对此理论之前途十分乐观。为 什么他讲这话?就是因为在那个以前大家吵得一塌糊涂,不知道是不是整个这个方向是错误的。 又譬如Pauli(泡利),当时一个非常有名的物理学家,他在1925年5月给了克罗尼格(Ralph Kronig)一封信,这信上面说“物理又进入死胡同,对我来说物理太困难了”。可是过了五个月以后又给克罗尼格写了一封信,他说Heisenberg(海森堡)的力学使得我复苏。
这上面所讲,我引的这些话就是要使得大家了解到当时成功跟失败的起伏是非常之大的, 这个现象恐怕是物理学史里面很少有的。又譬如Hans Kramers给Oskar Klein写了封信,这是1927年,这是在量子力学基本的一些文章已经发表了以后,在要讨论量子力学的解释的时候争辩的很凶, 玻尔跟海森伯两人特别争辩。那么Hans Kramers就给Oskar Klein了封信,他说“我们都太厚道,不可介入此争执,玻尔与海森伯都是坚持不让、步步紧逼的能手,会把我们压成碎片”。所以我想大家看了这个可以知道当时的空气。
在五十年代,大家也许知道R·Oppenheimer(罗伯特·奥本海默)是战时在美国主持原子 弹工作的理论物理学家,战后从1949年开始他变成普林斯顿高级研究中心的主任。我在那个 地方工作了17年,我跟他非常熟,他说他就是描述那个时代,也可以说是1925年以前的二十 年,他说“那是这个在实验室里耐心工作的时代,有许多关键性的实验和大胆的决策,有许 多错误的尝试和不成熟的假设,那是一个争执通讯与匆忙会议的时代,有许多激烈的辩论和 无情的批评,里面充满了巧妙的、数学性的挡驾方法。对于那些参加者,那是这个创新的时 代,自宇宙结构的新认识中,他们得到了激奋也尝到了恐惧。”(大家注意这句话“也尝到 了恐惧”),“这段历史恐怕永远不会完全记录下来,要写这段历史需要有像写Oedipus (奥迪帕斯),或写Cromwell(克伦威尔)那样的笔力,可是由于涉及的知识距离日常生活 是如此遥远,实在很难想象有任何诗人或史家能胜任”。
方才我跟大家介绍的是关于量子化的开始的二十世纪的发展,下面我给大家介绍一下对称。 对称这个观念在人类的历史上是非常古远的,而且在每一个不同的文明里头,在古代都有它 的发展历史。对称引用到科学是比较晚的,可是大量引用到物理学是二十世纪才有的一个现 象。对称用数学的语言跟不变性有密切的关系,比如你说一个东西是左右对称的,这句话可 以这样子解释,就是一张相片拿来,你把它反过来跟原来一样。把它反过来这件事情有不变 性,这个就是一个准确的史学语言来描述对称,所以对称跟不变性在数学的语言里头基本上 是一回事。对称深入地引入到二十世纪的物理学也是从爱因斯坦开始,爱因斯坦在1905年另 外一篇了不起的文章是狭义相对论的文章。他这个狭义相对论的文章里边从后来看,有一个 不变性,所以有一个对称,可是爱因斯坦自己并没有了解到这一点。爱因斯坦在1905年的文 章里头既没有Symmetry对称这个观念,也没有不变性这个观念。这个观念的引入是两年以后 一个大数学家Minkowski(闵可夫斯基)把它引进去的,Minkowski(闵可夫斯基)指出来爱 因斯坦1905年的文章里头有非常重要的不变性,而且这个不变性是把时间跟空间连接在一起 的。这个想法爱因斯坦起先抗拒,他曾经讲过,他说Minkowski(闵可夫斯基)的这个用数学 的观念来讲狭义相对论是Superfluous learnedness,我可以翻译成是没有用处的艰奥。可是 很快的爱因斯坦大概再想了一下以后,了解到这个想法是不对的,不但这样,他在以后就发 现这个想法不但是对的,而且要更深入地去研究。关于这点我们可以从以下这几句话看出来, 他在1950年,他71的时候写了一篇文章,上面讨论了他一生的科学研究的历史,他说“在 1908年我意识到狭义相对论也就是Lorentz(洛仑兹)变换下的不变性的要求太狭窄了”。这 个可以说是广义相对论的开始,就是这句话你看了以后就知道到1908年他已经了解到,他本 来抗拒Minkowski(闵可夫斯基)把不变性、把对成引到狭义相对论里头这个观点是不对的。 而且不但觉得Minkowski(闵可夫斯基)的想法是对的,很显然你看了这句话就知道他在 1908年开始要把这个扩充,他扩充到什么呢?他希望到一个不变性可以在一个非常广大的空 间里头,那么这个研究了七年到八年,在1915年或者1916年前后写出来了广义相对论。所以 你可以说,到了1925年、1926年物理学里头对于对称的了解已经大大深入了一步,可是这个 深入的一步远远的不够,其中一个很主要的道理是因为对称和不变性要引到理论物理学里头, 需要更多的数学的工具,这个数学的工具物理学家当时是没有的,这个数学的工具最重要的 一个叫做群论(Group Theory)。群论基本上是在十九世纪由一些数学家所发展出来的,物 理学家对于群论一直到一九一几年、一九二几年为止,是不太了解的,很少有人学过群论。 可是到了1925年,海森伯、狄拉克、泡利、玻尔,他们几个人引进了量子力学以后,物理学 家渐渐地了解了Group Theory群论在量子力学里头有非常重要的应用。那个时候推动Group 理论到物理学里头最重要的两位,一位是一个大数学家Hermann Weyl(赫尔曼·外尔),一 位是一个大物理学家叫做Wigner(韦格纳),从1925年到了1970年,这个对称就渐渐变成了 一个主题旋律,这个里头包含了对于群论的了解,对于对称跟不变性的了解。那么还有一件 事情是在1956年到1958年发现了宇称不守恒,宇称不守恒现象的发现是因为在那个以前大家 觉得对称既然这么重要,所以宇宙之间一定是极度对称的。那么这个想法当然在后来有些改 变,可是对于对称的重要性没有问题,还是大家都继续在接受着。可是在1954到1956年之间, 发生了一个谜,这个谜叫做(θ-τ)之谜。
我不必跟大家解释这是样一个谜,就发展说是当时的想法不太对,根据原来的想法,有一些基本粒子里头的现象不能了解,那么后来发现这个原因了,宇宙虽然非常对称,可是略微有一点点不对称的地方。那么这个略微有一点点不对称的地方就叫做宇称不守恒,那么这个实验方面是由吴健雄跟她所领导的一组实验工作者在1957年初所发现的。她曾经说她绝对不相信宇称不守恒,所以说她可以跟人打随便多少钱的赌,说吴健雄的实验一定证明宇称是守恒的。那么等到发现不守恒了以后呢,她就讲了“幸亏没有人跟我打赌,否则今天我没有够多的钱可输,现在这样我丢了些脸,可是我还有够多的声誉可丢”。也因为这样的缘故,所以在1957年、1958年到1959年这两年之间,对称在物理学里头的重要性达到了极高峰,而且知道对称不是那么简单,是既有对称常常又有小的不对称。
刚才我跟大家介绍一下对称到物理学在头半个世纪的发展,以下我跟大家介绍另外第三 个主题旋律,是相位因子。相位因子phase factor的观念最开始当然不是二十世纪的,是任 何有波动观念的理论都有相位的观念,不过从前对于这个相位的重要性没有足够认识。Dirac (狄拉克)是量子力学奠基人之一,在1972年他讲了这么一句话,在那个以前所有的人都认 为量子力学最重要的一点是不可译的noncommutative algebra。可是在1972年,在Dirac(狄 拉克)已经七十几岁的时候他说了“如果有人问我量子力学的主要特点,今天我会说,不是 noncommutative algebra,而是相位(Phase)”。然后他底下就讲了这个相位在量子力学里 头的重要性,总括讲起来他的意思就是说,在一个波动的里头要有相位的观念。比如说是你 可以把波峰做90度,波底做270度,然后再到一个波峰是360度加90度,这样子的一个相位的 改变,这个有任何一个波动的运动,这是很显然、很重要的一个观念。可是,在一个粒子、 一个电子在走的时候,或者是一个质子在走的时候就不显然要有相位的观念,可是通过了量 子力学,我们知道波动的理论跟粒子的理论其实是一回事情,所以整个物理学里头相位的观 念就变的非常的重要了。可是狄拉克刚才所讲的相位的观点在量子力学里头的重要性还不够 描述今天我们对于相位因子的重要性的了解,这个发展是在1918年由Hermann Weyl(赫尔曼·外尔)所引进的。那个时候Hermann Weyl受到了爱因斯坦的影响,爱因斯坦在那个以前两 年发表了广义相对论震惊了整个的物理学界。然后爱因斯坦就说,这个广义相对论对于引力 场有一些了解,广义相对论以前有Maxwell方程式对于电磁学有一些了解,应该把这两个合在 一起变成统一场论unified field theory。所以这是爱因斯坦所提出来的一个方向,而这 个方向在以后几十年是爱因斯坦一直想要促成的一个研究方向。那么爱因斯坦不在了以后, 今天还继续是理论物理学的中心问题之一。Weyl(外尔)比爱因斯坦大概年轻六岁,他受了 爱因斯坦这个想法的影响,他于是就想出来一个方法,要想把电磁学跟引力场连在一起,那 么他研究出来的理论现在叫做规范理论。规范的意思是大小,gauge是量的意思,规范理论英 文是gauge theory,为什么叫gauge theory呢?因为当初Weyl(外尔)是在想量一个东西, 那么把这个I加入以后呢,量这个东西就变成了相位。所以通过了Fock(福克)跟London (伦敦)以及后来Weyl(外尔)回来再写一篇文章以后,这个规范理论其实应该叫做相位理 论,而这个相位理论的基本中心思想就是底下的一句话,说是相位因子的随意性就给了电磁 方程,电磁方程Maxwell方程是1865年Maxwell所写下来的,这当然是人类历史上一个大的贡 献。可是Maxwell里头有一个内涵的对称性,这个对称性一直到刚才我进的1918年、1927年、 1929年,Weyl、Fock、London他们几个人的工作才使得大家了解,这个了解用一句话来讲就 是相位因子的随意性,什么叫随意性呢?就是说相位因子可以改,你改了以后不影响电磁方 程,这个观念是规范性理论的中心思想。
方才半个钟头我给大家介绍了三个主旋律,量子化、对称跟相位因子,到了二十世纪的 的后半世纪,可以说是主题主体的基本理论物理学的发展就是这三个主旋律的展开、变奏跟 交织。developments variation and interlace,非常有意思的是它们之间纠缠在一起, 我这个纠缠在一起,我想跟symphony music(交响乐)里边的development是很像的。这其 间有一个我特别要给大家提出来的是有一个公式,这个公式是Feynman的想法,Feynman把量 子力学的基础改写了一个方法,他引进了一个Propagator的观念,而这个Popagator写成一 个路径积分,Path integral写出来是这样的,这个我认为没有问题,是Feynman一生最重要 的贡献,Feynman有很多的贡献,研究生最容易注意到的是他的费曼图贡献。费曼图的贡献虽 然重要,我想远不如这个方程式的重要,因为这个方程式把量子力学的精神抓住了,而且这 个方程式非常有意思,把刚才我讲的三个主旋律都纠缠在一起。第一,你看这有个h,这就 是普朗克的常数,所以这个方程式与量子化有直接的关系。另外这个方程式整个是这样子的 一个积分,这个exp[i/h(activn)]就是一个相位因子,是一个更复杂的想法的相位因子。 而这个跟对称有什么关系呢?有极为密切的关系,跟规范对称有极为密切的关系。因为规范 对称我刚才是说在变的时候它的物理不变,那么这个通过这个路径积分是完全显示出来的, 所以我认为这个方程式是把刚才所讲的三个主旋律纠缠在一起写成一个方程式,这是非常妙 的一个方程式。而这个方程式我所以觉得它重要的原因,是因为这个方程式的数学意义到现 在还没有了解,这个路线积分到底是怎么一回事情,是到现在为止还没有一个严格的数学的 定义。所以我想这正是二十一世纪前一些年,年轻的物理学家可以在里头发展他的天地的地 方。
这个规范对称在一九二九年到五十年代之间,大家都了解它是很妙的,可是到了五十年 代中叶,这个规范对称需要推广,这个推广就把p-eA(p-eA是规范对称方程式里头的一个重 要的观念)稍微改变,变成p-eB。A是一个场,B是一个矩阵场,所以B比A稍微复杂一点,这 个方程式叫做非Abel规范场。Abel是一个大数学家,他是19世纪初年一个挪威人,他不幸在 二十几岁就过去了。那么他在群论早年做了一个非常重要的工作,所以很多的群叫做Abel群, Abel群的特点是它其中的两个元素可以对换,就是AB等于BA,AB等于BA的这种群叫做Abel群。 那么电磁场变成相位因子,那个相位因子是一个Abel群。刚才我说把A变成B,那个B是一个 方阵(矩阵)了以后,这一变成方阵(矩阵)以后它就不能够对换了,所以就变成非Abel群, 这个非Abel群所产生出来的规范场叫做non-Abelian gauge field。最近这二十五年以来, 高能物理里头的所有这些实验都是可以用非Abel规范场来描述的,不过中间加进了一个新的 一点,这点是对称破缺。因为这个缘故,所以我在七十年代的末年把这个归纳起来,我说这 个可以是讲成是对称支配相互作用。就是说所有的相互作用它的基本的方程式是由对称来决 定的,这个决定的方法就是非Abel规范场。这个话到现在大家都同意,可是还有一点没有解 决,就是怎么能够把爱因斯坦的广义相对论也变成一个非Abel规范场。所有的人都知道,这 两个的构造非常之类似,所以一定是一个非Abel规范场,可是这里头有一些到现在还没能解 决的问题,这也可以说是这二十年来基本理论物理学中心的问题,而这个问题我想还要延续 到二十一世纪。
另外,我觉得特别值得给大家提的是对称相位因子和纤维丛的观念,等到物理学家对于相 位因子非Abel比较从实际的出发,多了一些了解以后呢,忽然发现到原来在七十年代,整个 的数学结构与数学家已经发展了二三十年的一个观念,叫做纤维丛是有密切的关系。我个人 第一次了解到这两个有关系,是因为在1968年、1969年前后我在Stony Brook教广义相对论的时候,我就写了一个方程式,叫做Riemann curvature,这是广义相对论里边也是Riemann Geometry基本的观念。我把那个观念写在黑板上了以后,忽然发现原来这个方程式跟二十多年以前Mills跟我在1954年所写的非Abel规范场的方程式很像,所以下课以后我就仔细去研究到底有多么像,研究清楚了以后发现它不是像,它根本就是一回事情,只是要把一些观念稍微改一改,改了以后就完全一样了。所以我就去找了一个当时石溪(Stony Brook)的数学系主任,叫做James Harris "Jim" Simons(詹姆斯·西蒙斯),他当时是一个很有名的数学家,我告诉了他这些事情,他说这些都是纤维丛,我说什么是纤维丛呢?他就给了我一本书,这本书是一个叫做Steenrod的人写的(Steenrod, Norman (1951), The Topology of Fibre Bundles, Princeton University Press),非常有名的一本书,所以我就拿回去看,看了以后呢,不懂,因为这个数学家的语言现在非常之枯燥。所以后来有一次在南朝鲜一个演讲里头我就讲了这个故事,我说现在这个数学书只有两种,一种你看完第一页你就看不下去了,还有一种你看完第一句话你就看不下去了。不过非常惊人的,这个看不下去的纤维丛等到后来我了解了以后,确实是把规范场的精神给它吸收进去了,而这个发展从数学家的立场讲起来是非常自然的。所以这个数学跟物理的关系是一个非常微妙的关系,可是有不同的价值观,有不同的传统。而纤维丛的观念引进来很自然地就把拓扑学引进到物理里头。拓扑学是二十世纪的主流数学之一,可以说是以前的数学里头没有这个主要的观念。
总结一下,我给大家介绍了一下这三个主旋律,这三个主旋律直接影响了我们对于时间、空间、运动、能量、力量的基本了解。这个非常有意思的一件事情是,从非常长远的观点来 讲起来,这三个主旋律在很早的人类历史上都有过零星的讨论。比如说量子化,希腊人Democritus(德穆克里特)就已经讨论了原子,Zeno(芝诺)讨论了连续跟不连续的分野,中国的庄子在公元前300年左右也讨论了连续跟不连续之间的哲学的问题。可是这些量子化跟 二十世纪所讲的量子化有类似的地方,可是有个主要的不一样。这个二十世纪的量子化是运 动量的量子化,不是一个原子、分子的这种,那么这个所以说是把量子化的观念给它加了一 个重要的改变以后,这个是左右了二十世纪物理学发展的一个非常的元素。讲到对称的话, 那么希腊人对于对称是非常注意的,从公元前600年到公元前500年,尤其是Pythagoras,他 们对于圆的对称性,认为这个是支配宇宙一切的一切的最基本的元素。那么这个对称性到今 天发展来发展去,这个对称最重要的是非Abel的Lie group,所以这也是从一个很长远大家就 认识到的一个重要的观念里头,把它的细节了解了以后,把它变成准确的数学的语言的另外 一个例子。那么讲到相位呢,当然我们知道月亮的盈亏,四季的循环,这些都是任何一个古 文化里头都有的观念,可是今天特别重要的是相位因子的随意性,它的伸缩性,它虽然伸缩 但它不影响方程式的结果,这个是规范场的基本的观念。而这个观念注入到就相位因子以后, 就慢慢地产生出来今天的二十世纪的物理,谢谢。
- 20世纪数学和物理的分与和, 杨振宁,(YouTube)
- Quantization, 杨振宁, Lecture 1/16: Thematic Melodies of 20th Century Theoretical Physics, (YouTube)
- Phase Factor, 杨振宁, Lecture 2/16: Thematic Melodies of 20th Century Theoretical Physics, (YouTube)
- Symmetry, 杨振宁, Lecture 6/16: Thematic Melodies of 20th Century Theoretical Physics, (YouTube)
- Yang-Mills equations, 杨振宁, Lecture 10/16: Thematic Melodies of 20th Century Theoretical Physics, (YouTube)
- Thematic Melodies of Twentieth Century Theoretical Physics : Quantization, Symmetry and Phase Factor, CERN Document Server
- C. N. Yang: Stony Brook Masters Series
- (普通話) 楊振寧教授主講 Part I 學習生活
- (普通話) 楊振寧教授主講 Part II 我與恩師
- (普通話) 楊振寧教授主講 Part III 研究經歷
- 杨振宁在昆明的读书生活
- 我的学习与研究经历(杨振宁,PDF)
- 杨振宁先生与复旦大学物理系教师的座谈(PDF)
- 物理学之美:杨振宁的13项重要科学贡献,施郁(复旦大学物理学系)(PDF)
- Conservation of Isotopic Spin and Isotopic Gauge Invariance (C.N.Yang and R.L.Mills)
- 爱因斯坦、物理学和人生——杨振宁先生访谈录
- Scientific and Related Works of Chen Ning Yang
- SELECTED PAPERS (1945-1980) With Commentary 2005 Edition (Google Books)
- 一位理论物理学大师人生的第二个春天 - 读杨振宁先生Selected Papers II With Commentaries 有感(朱邦芬, PDF)
美与物理(杨振宁)
十九世纪物理学最重要的两个贡献,一个是电磁学,一个是统计力学。统计力学最主要的创建人是三个,一个是麦克斯韦,一个玻尔兹曼,一个叫做吉布斯,其中玻尔兹曼写过很多通俗的文章,那么我今天就从他的一段话来跟大家开始谈谈。他说,"一个音乐家在听到几个音节以后,就能辨认出来莫扎特、贝多芬或者舒伯特的音乐,同样一个数学家或物理学家,也能在念了几页文字以后,就辨认出来柯西、高斯、雅可比、亥姆霍兹或者克尔期豪夫的工作",他的这段话我觉得很有意思,为了解释这段话,我曾经跟几个朋友讲这样几句,我说,"大家知道,每一个画家、音乐家、作家都有他自己独特的风格,也许有人会以为,科学与文艺不同,科学是研究事实的,事实就是事实,什么叫做风格,要讨论这一点,让我们拿物理学来讲,物理学的原理有它的结构,这个结构有它的美跟妙的地方,而各个物理学工作者对于这个结构的不同的美跟妙的地方的感受,有不同的了解,因为大家有不同的感受,所以每一个工作者就会发展他自己独特的研究方向跟研究方法,也就是说他会形成他自己的风格",那么这段话我希望在底下几十分钟给大家详细解释一下。为了做这件事情,我先给大家介绍两个二十世纪的大物理学家,第一位叫做狄拉克,他是英国人,1902年出生,是一个非常有意思的人,他很少讲话,而你要听他讲话的话,你觉得他这个想法跟一般的人都不一样,那么关于他的故事非常之多,所以我给大家只讲一两个。狄拉克讲话很少,他讲话了你要听的话,他有他自己的思维方法跟他的逻辑,我给大家只举两个例子。
第一个例子,是他有一天在演讲,演讲完了以后有个学生说"狄拉克教授,我不懂你刚才这个所讲的理论",于是狄拉克就又解释了一下,解释完了以后,那个学生说"狄拉克教授你刚才讲的这个,跟你以前所讲的每一个字都是一样的",狄拉克说"这不稀奇,因为这是最好的讲法"。另外一个故事是,他在普林斯顿的一个演讲,普林斯顿的介绍他的教授,在他演讲完了以后就说"狄拉克教授可以回答你们的问题",有的学生就说"狄拉克教授你刚才那个方程式(3),是怎么从方程式(2)演化出来的?",狄拉克不讲话,于是介绍他的人等了几分钟,就说"狄拉克教授,请你回答他的问题",狄拉克说"他只讲了一句话,他没有问问题"。
狄拉克最重要的工作,是在1928年,他写了一篇文章,这个文章上面有一个很简单的一个方程式,一个非常简单的一个方程式,可是这个方程式有不得了的贡献,它奠定了今天原子、分子结构的基础,它解释了为什么电子有自旋,自旋的意思就是每一个电子都是在那儿象陀螺一样在那儿转,电子有自旋这个事情不是狄拉克发现的,在那以前几年,已经有人提出来,电子一定有一个自旋,可是不知道为什么要有自旋,刚才我说的这个简单的方程式,你去了解了它的真正的意义以后,你自然而然就知道,电子一定要有一个自旋。而且这个电子的自旋跟自旋在一起的是一个磁矩,就是象一个小磁铁,这个磁铁,电子这个有自旋有磁铁这件事情也不是狄拉克发现的,是当时已经知道了,可是没有人知道为什么要有磁矩,而用刚才所念出来这个方程式就很自然的知道有磁矩,而且这个磁矩可以定量的用这个方程式算出来。而且这个磁矩跟电子轨道行动的关系,也是一个本来猜想到了,可是不懂为什么缘故是那样,也是被他的这个方程式所解释了。你想这样简单的一个方程式,把当时困扰大家的三个重要的问题都解决了,所以这个当然是震惊了当时物理学界。
Dirac equation,http://en.wikipedia.org/wiki/Dirac_equation
我想最好的方法来描述这个,就是这是一个神来之笔,可是这个神来之笔并不这么简单,就被所有的人都认为是绝对对的,因为它出了一个新的问题,这个新的问题叫做负能问题,Negative energy,大家知道通常"能"都是正的,他这个方程式,你去算了一下以后,会得出来一个非常稀奇的现象,说电子可有负能,这个负能当时是不可思议的一件事情,所以很多人懂了他的这个工作的第一步以后,觉得这个东西是妙不可言,可是又觉得这个里头有非常奇怪的、不能够了解的、绝对不会对的事情,那么所以以后几年,就有种种人批评狄拉克,说他这个工作,看起来对是碰巧,其实是不对的。可是狄拉克坚持,到了1931年,他更进一步,他说"不但这个负能是应该有的,而且有了这个负能以后,就会发现一个新的,重要的一个现象",当时还没有看见,就是说任何一个电子,都会跟它俱来的有一个叫做反粒子,anti-particle,每一个粒子都有一个反粒子,这个反粒子跟这个粒子完全一样,可是它的电荷是相反的,这个当时又是大家所不能接受的。人家说你从来没有看见过任何一个反粒子,你怎么随便就讲有个反粒子呢?可是过了一年以后,加州理工大学有一个年轻的,他其实是博士生,叫做卡尔·安德森,他在第二年,用云雾室照出来了一个轨道,这个轨道是一个正电子,就是正是刚才所讲的,狄拉克所讲的电子的反电子,因为它反粒子,因为它是带着正电,这一来的话,大家知道狄拉克的这个方程式不但是对,而且完全是对的,他预言出来了一个从前大家不晓得的一个新的现象。
所以,如果你想一想狄拉克,他是一个人话讲得很少,可是他话的内涵有简单的、直接的、原始的逻辑性,懂了他的想法以后,你会拍案叫绝。我想了想,用什么样子的中国的传统的话,可以描述看了他的文章以后,叹服了他这个工作的重要性以后的对于他这个文章的看法是什么,我想最好是说"秋水文章不染尘",因为他的这个文章确实是里头一点渣滓都没有的,是清楚极了,假如你懂他的逻辑的思维方法。
我曾经想,要想跟我的文史的朋友介绍看了狄拉克的文章的感受,应该怎么样讲法呢?那么最后我发现到了,唐朝的诗人高适,他有一首诗《答侯少府》,上面有这样两句"性灵出万象,风骨超常伦",我觉得这两句话用来形容狄拉克的风格是最好的。为什么呢?"性灵出万象",这个"万象"用来描述狄拉克方程式的影响,那是再恰当不过了,它解释了无数的物理、化学的现象,它是今天的原子、分子结构的最重要的一个方程式。为什么说"风骨超常伦"呢?这也是我刚才已经跟大家大概介绍了一下,他在1928年到1932年四年之间,他不顾当时最有名的几个物理学家的反对,的冷讥热嘲,这几个最有名的物理学家,包括尼尔斯·玻尔,包括海森伯,包括泡利,他们都是在嘲笑狄拉克,说狄拉克想入非非,他做的东西是不对的,可是这个狄拉克是坚持的,所以他确实是"风骨超常伦"。那么什么叫做"性灵"呢,"性灵"据我所知道,是在明朝公安派的文学批评家"三袁",他们所最早提出来的,其中袁宏道讲他的弟弟袁中道的诗,我念这个他讲他弟弟的诗,"独抒性灵,不拘格套,非从自己胸臆流出,不肯下笔"。这几句话拿来形容狄拉克的风格是最恰当不过了。
底下我要给大家介绍另外一个二十世纪的大物理学家,叫做海森伯,我想很多人会以为海森伯比起狄拉克还要略胜一筹,海森伯是德国人,1901年出生,1976年过去的,我也带了一个海森伯的相片,这个是他24岁的时候还没有做出来他最重要的工作的时候的相片,今年12月,是他的100周年生日,要在慕尼黑有一个庆祝。
他所做的工作是开始了量子力学的第一步,二十世纪物理学里头,最最重要的几个发展里头之一就是量子力学,在二十世纪以前,物理里头的数目、数据都是连续的,你说是这个东西的家数是A,这个A是一个连续的,不是一个是跳跃的,可是在二十世纪的头二十年,发现到这个跟原子、分子物理不符合,所以后来就产生出来量子的这个观念。可是量子化的这件事情是一个非常困难的,因为要把牛顿,从牛顿开始建立起来的物理系统整个要改观,那么这个革命性的发展不是一天两天所能做到的,所以二十世纪头25年是有种种的纷扰。在50年代美国一个重要的物理学家叫做奥本海默,大家也许晓得,奥本海默非常有名的地方是因为他在打仗的时候主持了美国的原子弹的制造的工作,他是非常会讲话的一个人,他在50年代在英国的一个演讲里头,描述了那个头25年物理学的一个工作者之间的一个空气,他说,"那是一个在实验室里耐心工作的时代,有许多关键性的实验和大胆的决策,有许多错误的尝试和不成熟的假设,那是一个真挚通讯与匆忙会议的时代,有许多激烈地辩论跟无情的批评,里面充满了巧妙的数学性的挡驾方法,对于那些参加者,那是一个创新的时代,自宇宙结构的新认识中,他们得到了激奋,也尝到了恐惧,这段历史恐怕永远不会被完全记录下来,要写这段历史需要有象欧迪帕斯或象克伦威尔那样的笔力,可是由于涉及的知识距离日常生活是如此遥远,实在很难想象有任何诗人或史家能胜任"。
所以这二十几年的经历确实是被奥本海默所描述的很恰当的,那么在那样困难的时候,一个年轻的24岁的海森伯出现了,他写了一篇文章,这个文章象一个方向迈了一步,这个方向现在叫做量子力学,而这个方向后来发扬光大,就变成了二十世纪以后的几乎是全体物理学里头最最重要的几个原则之一。年轻的海森伯怎么忽然能够走了这一步,从前人没有走过的呢?他在晚年的时候,曾经有过一篇文章上讲这个经历,海森伯喜欢爬山,所以很自然的他就把爬山拿来做一个例子,他说"爬山的时候,你想爬某个山峰,但往往到处是雾,你有地图或别的缩影之类的东西,知道你的目的地,但是人堕入雾中,不知道要向什么方向走,然后忽然你模糊的自雾中看到一些形象,你说哦,这就是我要找的大石头,整个情形从此而发生了突变,因为虽然你仍然不知道你能不能爬到那块大石,但是在那一瞬间,你说我现在知道我在什么地方,我必须爬近那块大石,然后就可能知道该如何前进了",他这几句话确实是描述了他的第一篇文章里头所讲的事情,因为他并没有完全懂他在第一篇文章里所讲的,他是一个尝试,是一个很模糊的一个印象,他这个文章写出来了以后,他要去渡假,他就把它留给他的导师叫做玻恩,玻恩比他年长了十几岁,玻恩有数学的修养,是海森伯所没有的,玻恩看了他这个文章以后,知道海森伯里边所讲的数学,是一个从前物理学家没有用的数学,叫做矩阵,海森伯因为数学修养不够,所以不知道他所做的东西是矩阵,结果玻恩就跟另外一个比较年轻的物理学家写了一篇文章,然后海森伯回来了以后,他们三个人又合写了一篇文章,这三篇文章奠定量子力学的基础,今天物理里头叫做one man paper 、two men paper、three men paper,这三篇文章的开始,就是量子力学的奠基的地方。
量子力学是物理学史上的大革命,我想也是人类的历史上一个大革命,不讲它对于纯粹物理学的贡献,单讲大家可以了解到的对于日常生活的贡献,核能发电、核武器、激光、半导体元件以及今天的计算机通信工程,所有这些工程都不可能发生,假如没有量子力学。海森伯24岁的时候写了这个文章,到了26岁,他就变成莱比锡(大学),理论物理学系的主任,他爱打乒乓球,打得很好,所以独霸那一系,而他是很好胜的,一直到一个从美国来的博士后,这个博士后来了以后,海森伯只得屈居亚军,打败海森伯这位乒乓球的博士后的名字,我想大家都是熟悉的,叫做周培源。
那么,海森伯跟比如说狄拉克之间的关系是什么呢?他们的关系很好,可是也有激烈的竞争,因为他们都是站在最前沿上面的,所以他们都知道对方的工作是非常重要的,所以每一个工作都仔细注意。在1928年狄拉克写出来了他的,刚才我给大家介绍的狄拉克方程式以后,海森伯跟泡利,泡利是他最熟的物理学家朋友,不懂狄拉克怎么能够想出来他这个奇怪的方程式,因为这个方程式是历史上从来没有人向那个方面写的,所以他们不懂。那么,因为这样子,他有点困扰,今天我们可以从海森伯给他的朋友泡利写的一封信上面看到他当时的心情。他的信上面说"为了不持续的被狄拉克所烦扰,我换了一个题目做",这就是代表他跟泡利不懂,这个狄拉克怎么能够出这种稀奇的想法,而得出来非常重要的结果,那么海森伯在这封信上说我换了一个题目做,然后底下说得到了一些成果,这个成果又是一个惊人的贡献,大家知道为什么有磁铁?磁铁里头有很多电子,那些个电子自旋都向同一个方向,所以整个加起来,它的磁矩加起来就变成了一个磁铁。可是为什么缘故,什么力量使得这许多磁矩向一个方向走呢?这个是当时不懂的,而且是一个困扰了很久的题目,海森伯,他说他换了一个题目,他就是不去研究一个一个电子的结构,他去研究很多电子的结构的时候,他看出来一个苗头,这个苗头就是今天我们了解为什么磁铁能够成为磁铁的道理,所以这又是一个极为重要的工作。
如果我们总结一下,狄拉克跟海森伯的不同的地方,那么第一样我们就了解到,狄拉克的研究方法跟海森伯的研究方法是很不一样的,狄拉克的研究方法可以说是循着独特的、新的逻辑,无畏地前进,这是他的风格;海森伯的研究方法,就象他刚才我给大家念的故事里头所讲的,你觉得他的文章是在雾里头摸索,这是他的一个文章给你的一个感受。狄拉克的文章你看了以后,跟海森伯的文章看了以后,有相同的地方,有不同的地方。相同的地方是,他们都可以出其不意,有极强的独创力,向一个从前人没有想象的方向走,这是他们共同的地方。他们不同的地方呢?是狄拉克的文章非常清楚、非常直接,你看了他的文章觉得里头没有渣滓,相反的,海森伯的文章是朦胧、绕弯、不清楚,而且有渣滓。你看了狄拉克的文章了,你觉得这个领域已经没有什么东西可以做了,因为凡是正确的话,狄拉克都讲过了。海森伯的文章完全不一样,他的每一篇文章里头,会有非常深入的见解,也有错误的想法,所以,海森伯的文章必须要仔细看,你如果能够把海森伯文章看了,知道他哪个是对的、哪个是不对的,你就可以把他不对的那个改正了,得出来很重要的贡献。所以他们这个文章给你看的,感受是不一样的。
那好了,当然你就会问了,说是为什么两个这么聪明的大物理学家,他们的风格会这样不一样呢?我想,这一部分当然没有问题是他们的个性不一样,海森伯的个性比较不接近数学,狄拉克的个性比较接近数学,比较接近数学的价值观,可是这个还不是唯一的道理,另外还有个道理,是与物理自己的结构有密切的关系,物理学现在是很大的一个学问,我觉得可以分成三个领域。
第一个领域是实验的领域,我们叫它叫"(1)";第二个领域叫做唯象理论,我们叫它叫"(2)";第三个领域叫理论架构,我们叫它叫"(3)",而这个理论架构呢是跟数学比较接近的,我们叫它叫"(4)"。如果你用这样子的一个宏观的分野来看的话呢,那么就觉得原来这个历史的发展,是与这个分野有很密切的关系。
海森伯在年轻的时候,他不喜欢数学,我刚才已经跟大家讲过了,他的一个最重要的文章写的时候,他没有学过方阵,是后来那个two men paper跟three menpaper才把他所做的事情跟方阵连在一起。可是到了海森伯晚年,他改过来了,通过了几十年的经验,他了解到数学是非常重要的,他在74岁的时候,写的一篇文章上讲,"1921、1922到1927年间,我们经常讨论,可是总是遇到各种矛盾与困难,我们就是无法理性的方法来解决这些困难,有人赞成波动理论,有人赞成粒子理论,所以后来有了一个数学结构的时候,这个数学结构就是量子力学,实际上我们的心态已达到了十分沮丧的地步,这个数学结构对我们来说是一个奇迹,我们看到了数学能做出我们做不出的东西,那当然是一个非常奇异的经历",请大家注意这句话,"数学能做出我们做不出的东西",这句话就表示了他当时的心态,他们左冲右突做了很多年,包括他们的老师,前后做了二十几年,可是做不出来东西,觉得实际的实验的结果跟以前的想法有对的地方、有不对的地方,是一种非常困难的地方,所以当时他们觉得他们已经没有办法了,忽然引进了矩阵这个观点以后,数学做出来了我们做不出来的东西,这就是他晚年回想他在24岁时候的工作的时候的一个感受。
既然讲到数学跟物理有这么密切的关系,当然可以问,数学跟物理整个的关系是什么呢?或者可以问,是许多同学,物理系的同学常常要问的,是说"我作为物理系的学生,我应该学多少数学?",这个是一个很复杂的问题,不能有一个很简单的解释,我曾经想过,我把数学跟物理的关系,比喻做两个树叶子,一个树叶子向这个方向,一个树叶子向这个方向,一个是物理,一个是数学,这两个叶子是大多数的地方都是不重叠的,可是在根的地方有一小块地方是重叠的,这一小块地方不是很大的,只是占每一个领域的也许5%、10%这样子,在这个重叠的地方,非常奇怪的,是这两个领域,享有共同的观点,所以它们在根源上面的关系是非常密切的,可是,我底下要讲的,虽然物理与数学有如此密切的关系,可是二者共同的地方并不多,它们有各自的目的跟截然不同的价值观,以及不同的传统,在最基本观念的层面,他们令人惊讶的共享某些观念,但是即使在这个领域里头,这两个学科的生命力仍然按着各自的脉络成长,一个向这个方向走,一个向这个方向走。把这个落实到对于研究生的建议是什么呢?就是假如你是念物理的研究生,那么你必须要对于这个根源的这个地方有一些了解,可是,更重要的,除了你对于这个了解以外,你要了解到要向前途是什么方向发展,换句话说,你要了解物理的价值观,假如你不了解物理的价值观,那么你很可能是走到另外一个方向去了,当然走到另外一个方向,你在数学上做很大的贡献也很好,不过这也许与你当初想要做一个好的物理学家的初衷略微不一样就是了。
关于数学跟物理之间的分别,爱因斯坦在他的晚年也有过很有意思的一个分析,他问,因为他的一生的工作对于物理跟数学后来都有极大的影响,那么,他在晚年的时候问了他自己这样一个问题,说为什么他做了一个物理学家,而不是做一个数学家,他说"在数学领域里头,我的直觉不够,不能辨认哪些是真正重要的研究,哪些只是不重要的题目,在物理领域里头,我很快学到怎样找到基本的问题来下工夫",这几句话对极了,因为在他26岁的时候,在一个很不重要的瑞士伯尔尼的一个专利局里头做一个小职员的时候,他写了三篇震惊世界的文章,这三篇每一篇都引导出来物理学里头的一个革命,这就是代表他有一个直觉的观念,知道物理里头哪一个是最重要的问题,哪个是琐碎的、没有什么大意义的问题,而他的这个能力,能够辨别到什么是重要的问题,什么是不重要的问题,在历史上我想只有牛顿能够跟他比。
让我现在回到主题,"美与物理学",物理学我刚才讲了有三个领域,大的领域,(1)、(2)、(3),这三个领域,每一个领域有不同的美。先讲在实验,比如说是我们讲虹跟霓,我想在座每一位,小时候看见了虹跟霓都会说这是非常之美,等到你年纪稍微大了一点的话,你如果会做实验的话,那么你可以量那个虹是多少度,霓是多少度,你如果去量了以后,你就发现虹是42度,就是它这个角是42度,而霓是50度,而且你继续观测以后,你就知道红在外、紫在内,霓是反过来的,是红在内、紫在外,这些都是你观测了以后了解到的,这个非常美妙的现象是实验的美。可是你进步到了唯象理论以后,你就懂为什么会有虹和霓呢?是因为太阳光在水珠子里头可以有一个全反射,一次全反射就出来虹,两次全反射就出来霓,而且你经过全反射这个计算可以算出来,一个是42度、一个是50度,这个是唯象理论的美,我想任何一个学生,第一次算出来这个42度和50度的时候,不可能没有一个非常深的感受,觉得这真是妙不可言。可是这个还不够,为什么要有全反射、为什么要有折射?这些要到理论架构里头,到了麦克斯韦方程出现以后,你就可以了解到,为什么缘故要有全反射,而且可以知道为什么在水里头要有折射,这个把它的根源找出来,所以这个是更高层的美。
今天我们如果看物理学的理论架构,上边有,里面有也许八九个、九十个方程式,其中刚才我给大家已经介绍了狄拉克的方程式,我也给大家大概介绍了海森伯方程式、麦克斯韦的方程式、牛顿的方程式、爱因斯坦的方程式,这许多方程式里边所描述的是宇宙的秘密,这些许多方程式,大可以讨论到星云群里头的现象,小可以讨论到基本粒子里头的内部的结构,时间长,可以讨论到十亿年,短,可以到十的负二十七次方秒,这样子大的,这么多包罗万象的东西,它的解释都建筑在这几个支柱上边,所以,而且他们都是非常浓缩的语言,所以我想了解了这些以后,你会同意我讲这几个基本的结构是造物者的诗篇。说它是诗不只是因为它们是非常之浓缩的语言、浓缩的符号,还因为它们的内涵,往往随着物理学的发展而产生新的、当初所完全没有想到的意义,比如说是爱因斯坦在1916年写出来他的"广义相对论"的时候,他并没有能够完全了解到那个里边的含义,而这个含义最近这三四十年,通过宇宙学的发展,比如说是黑洞,这个里头有非常深邃,现在还没有能完全了解的一些新的内涵,那么这个当然跟诗一样,你们大家都晓得你在10岁的时候所念的诗,到20岁时候再看,原来10岁时候没有完全懂,你到30岁时候再看,你就了解到你20岁的时候也还没有完全懂这个诗,诗有这个现象,而刚才我所讲的这几个基本结构是也有这个现象的。所以我想如果要描述一个学物理的人或者是一个做物理工作的人,在了解到一个基本的结构的时候是什么感受?最好用诗人的话来描述。200年以前威廉·布莱克曾经说"To see a World in a Grain of Sand,Anda Heaven in a Wild Flower, Hold Infinite in the palm of your hand AndEternity in an hour ",这个台湾有一个散文家把它翻译成一粒沙里有一个世界、一朵花里有一个天堂,把无穷无尽握于手掌,永恒宁非是刹那时光。
在牛顿过去的时候,一个大诗人蒲柏写了这样两句"Nature and nature'slaw lay hid in night:God said,let Newton be!And all was light。",我把这个翻译成"自然与自然规律为黑暗隐蔽,上帝说让牛顿来,一切遂真光明",这些用诗人的语言来描述物理学的美,当然是描写得很好,可是我觉得不够,一个对于物理学的基本结构了解,知道它们能够对于那么多的复杂的现象给一个那么准确的解释的时候,还有一些美的感受,这个感受是诗人所没有写出来的,是什么感受呢?是一个庄严感、是一个神圣感、是一个第一次看见宇宙的秘密的时候的畏惧感。那么我想这个所缺少的感,正是哥德式建筑的建筑师,他们在设计哥德式这个建筑的时候,他们所要歌颂的,他们所要歌颂的是崇高美、灵魂美、宗教美、是最终极的美。
杨振宁中国农业大学自述:我的学习与研究经历
杨振宁,诺贝尔物理学奖获得者,清华大学高等研究中心名誉主任,美籍华裔科学家。历任普林斯顿高等研究所教授、纽约州立大学石溪分校理论物理研究所所长。先后获得中国科学院、美国国家科学院、台湾中央研究院等院士荣衔。1922年出生于安徽合肥,1948年获芝加哥大学博士学位。1957年,杨振宁与李政道因共同提出宇称不守恒理论而获得了诺贝尔物理学奖,二人成为最早获得诺贝尔奖的华人。精彩摘要:
与同学讨论是深入学习的极好机会。多半同学都认为,从讨论得到的比老师那里学到的知识还要多,因为与同学辩论可以不断追问,深度不一样。
一个人最好在研究开始的时候,进入一个新领域,就像挖金矿,挖新矿容易出成果,如果一个地方人家已经挖了五年,要想再挖出新矿,就比较困难。
中国教育哲学讲究“知之为知之,不知为不知,是知也”,知道的,不知道的,都要想清楚,这才是真正的学习。这种教育哲学,有很大好处,也有很大坏处。
一个社会要想科学非常成功,是不是必须制造一种风气,使年轻科学家都很冲,朝中国儒家君子相反的方向走?这是一个很深层次的问题,值得大家注意。
杨振宁讲座实录:
少年读到《神秘的宇宙》开启对物理的兴趣
当直觉与书本知识有冲突,是最好的学习机会,必须抓住,把本来的直觉错误想清楚,形成新的直觉
我1929年到清华大学,当时7岁,就读清华大学里的成志小学(编者注:清华附小的前身),我父亲是清华大学数学系教授。
4年后进入北京城里的崇德中学,现在叫北京市第三十一中学,在宣武门附近。学校很小,差不多300个学生,有一个小图书馆,我喜欢到里面浏览书籍。初中二年级,我在图书馆发现一本翻译过来的书,叫《神秘的宇宙》,描述1905年物理学大革命、1915年相对论和1925年量子力学,这不只是20世纪物理学的大革命,也可说是人类知识历史上非常重大的革命。我当时并不太懂其中的内容,不过产生了浓厚兴趣,这与我后来学习物理有密切关系。
1937年夏天我刚刚读完高一,抗战就开始,我们全家搬回合肥老家。后来清华大学与北京大学、南开大学合并,成立西南联合大学,我父亲到昆明就职,1938年春天,我们就到了昆明。当时中学生流离失所的很多,教育部就规定不需要有中学毕业文凭也可以参加高考,我当时高二,算便宜一年,参加高考就进入了西南联大。
高考考试科目中有物理学,我高中并没有学习物理学,就借了一本标准教科书,关门念了一个月,原来我非常喜欢物理,觉得更合我的口味,所以就进入西南联大读物理学,而我起初报考的是化学。
在大学,教科书说圆周运动是向心的,与我的直觉不一样。思考一两天后,才了解到原来速度向量不单包含量,还有方向,把方向改变加在其中,圆周均匀加速就变成向心。这个教训非常重要,当直觉与书本知识有冲突,是最好的学习机会,必须抓住,把本来的直觉错误想清楚,形成新的直觉。这是真正懂得一门学问的基本过程。
吴大猷、王竹溪两位师长引领进入研究领域
与同学讨论是深入学习的极好机会。多半同学都认为,从讨论得到的比老师那里学到的知识还要多,因为与同学辩论可以不断追问,深度不一样
大学四年级需要写学士论文,我去找吴大猷先生(编者注:著名物理学家,被誉为中国物理学之父,2000年去世),他给我的研究题目是“对称”,在物理学中用准确的数学语言表述就叫“群论”。“群论”在20世纪被用到物理学,成为显学。
吴大猷把我引到对称与群论领域。我学到群论的美妙和在物理中的深入应用,对后来工作有决定性影响,对称理论是我一生的主要研究领域,占我研究工作的三分之二。
1942年我取得学士学位后,进入清华大学研究院读硕士,硕士论文导师是王竹溪(编者注:物理学家、教育家,曾任北京大学副校长,1983年去世)。王先生的专长是统计力学,属于物理学一支。统计力学是我另外一个研究领域,占我一生工作的三分之一。
我在研究院的同班同学有黄昆(编者注:著名物理学家、中国固体和半导体物理学奠基人,2005年去世)和张守廉(编者注:著名电机工程专家,纽约州立大学石溪分校电机系主任)。我在黄昆70岁的时候写过一篇文章,描述当时我们无休止的辩论物理题目。记得有一次我们所争论的是关于量子力学中“测量”的准确意义,从喝茶开始辩论,到晚上回到学校,关灯上床,辩论仍没有停止。现在已经记不清争论的确切细节,也不记得谁持什么观点,但我清楚地记得三人(编者注:杨振宁、黄昆和张守廉)最后都从床上爬起来,点亮蜡烛,翻看海森堡的《量子论的物理原理》来调解辩论。
根据我读书和教书得到的经验,与同学讨论是深入学习的极好机会。多半同学都认为,从讨论得到的比老师那里学到的知识还要多,因为与同学辩论可以不断追问,深度不一样。
求学美国奔着敬重的诺奖得主费米选择芝加哥大学
一个社会要想科学非常成功,是不是必须制造一种风气,使年轻科学家都很冲,朝中国儒家君子相反的方向走?这是一个很深层次的问题,值得大家注意
1944年我研究生毕业,教了一年中学。1945年第二次世界大战结束,经印度到美国,进入芝加哥大学。当时中国与美国之间不但没有航班,也没有轮船。美国当时在亚洲有几百万士兵,所以美国就造了一些5000吨左右的船,从印度把兵运回美国,每个船中有一二百个舱位留给非美国军人。我们20几个公费留美学生在印度等了两个月,经印度洋、红海和地中海,最后到达美国纽约。到纽约后我请求进入芝加哥大学。
我在西南联大学的物理学已经相当高深,那时我最佩服3个20世纪重要的物理学家,一个是爱因斯坦(Einstein);一个是狄拉克(Dirac),英国物理学家;第三个是恩芮科·费米(Enrica Fermi),意大利出身,37岁时就获得诺贝尔奖。
费米在芝加哥主持建立世界第一个原子反应堆,他是第一流的实验物理学家,也是第一流的理论物理学家。事实上,物理学家在19世纪以前是理论与实验都要做的,牛顿既研究理论又做实验,可到20世纪,理论与实验变得更复杂,很少有人能够两方面兼做。20世纪能够在两方面都做出第一流工作的物理学家就是费米。
去美国的路上,我就想好跟着费米做博士论文,而且要做实验论文。我在西南联大物理学理论学得很好,实验却根本没有经验,而物理学最后是要基于实验的,所以想跟费米做实验方面的博士论文。
1946年初我到芝加哥大学,开学后就上了费米的课,很快熟起来。我提出跟着他做实验论文,他研究了一下说不行,因为他的实验不在芝加哥大学,而是在40公里以外的一个实验室,当时是保密的,所以我就没做他的研究生。
2001年是费米诞辰一百年,我在庆祝会中做演讲。我说,费米是20世纪所有伟大的物理学家中最受尊重和崇拜的人之一,他之所以受到尊敬和崇拜,是因为他在理论物理和实验物理两方面的贡献,是因为他领导下的工作为人类发现了强大的新能源,而更重要的是因为他的个性。他永远可靠和可信,永远脚踏实地,他的能力极强,却不滥用,也不哗众取宠,也不小瞧别人,我一直认为他是一个标准的儒家君子。
一般来讲,美国重要的科学家比较冲,同时,美国科学又是非常成功的。所以,这就出现一个问题,一个社会要想科学非常成功,是不是必须制造一种风气,使年轻科学家都很冲,朝中国儒家君子相反的方向走?这是一个很深层次的问题,值得大家注意。
感受中西教学方法差异
中国教育哲学讲究“知之为知之,不知为不知,是知也”,知道的,不知道的,都要想清楚,这才是真正的学习。这种教育哲学,有很大好处,也有很大坏处
在物理学习方法上,芝加哥大学与国内有一个基本的区别,国内是推演法,在书上学到一个理论,按定律推演到现象。芝加哥大学正好相反,不是从理论而是从新的现象开始,老师和同学脑子里整天想的就是这些新现象,能不能归纳成一些理论。如果归纳出来的理论与既有理论吻合,那很好,就写一篇文章;如果与既有理论不符合,那更好,因为那就代表既有理论可能不对,需要修改。
整个气氛与国内是不一样的。我觉得自己非常幸运,在中国使用推演法,打下一个非常扎实的根基;到美国,学会多注意新现象,由新现象归纳出理论。
中国教育哲学讲究“知之为知之,不知为不知,是知也”,也就是说你得知道自己所知道的,与不知道的东西分清楚,不能够乱七八糟。有些东西你是知道的,有些东西你不知道,都要想得清清楚楚,这个才是真正的学习。这是中国传统的教育哲学,很重要,有很大好处。 可是这种教育哲学也有很大坏处,事实上有许多知识不是这样学来的,比如一个小孩学讲话,并不是按部就班,甚至不知道自己已经学会,他在一个不太清楚的时候,就弄出来。关于这一点,我给它起一个名字叫渗透性学法,渗透性学法是中国传统不喜欢的。
事实上,很多东西第一次听不懂,第二次再听,还是不懂,可是就比第一次多懂了一点,等听到很多次以后,就忽然一下子了解,这是非常重要的学习方法,也可以说是中国传统教育哲学与西方教育哲学一个很大区别。我上学时就觉得西方学生没有把东西想清楚的习惯,可这并不阻止他们做出非常重要的工作,尤其是非常聪明的年轻人,用渗透方法吸取知识的能力很强。
芝加哥大学当时是非常成功的,研究气氛浓厚,有很多讨论会,多注重新现象,新方法,少注重书本上的知识。1948-1950年在芝加哥大学获得博士学位的毕业生中,有4位获得诺贝尔奖,这与当时浓厚的学习气氛密切相关。
1971年我到中国参观访问,中国大学的课程是非常之深,有所谓“四大力学”(编者注:传统的《理论力学》、《电动力学》、《量子力学》和《热力学、统计物理》组成),每一名物理系学生都要花很长的时间去学这四门理论课。四大力学当然重要,没人能否认它们是物理学的骨干,不过物理学不只是骨干,只有骨干的物理学是一个骷髅,有骨头又有血肉的物理学,才是活的物理学。
研究方向在“希望破灭”中清晰
一个人最好在研究开始的时候,进入一个新领域,到一个旧领域当然也可以,可是就像挖金矿一样,挖新矿容易出成果,如果一个地方人家已经挖了五年,要想再挖出新矿,就比较困难
1946年上半年,经过费米推荐,我成为泰勒(E·Teller,编者注:出生于匈牙利的美国理论物理学家,被誉为“氢弹之父”,2003年去世)的研究生。泰勒给我一个研究题目,几个星期以后,我给他看计算结果,泰勒觉得很好,还安排我做一个报告,大家的反应都非常好。泰勒说可以把它写成一篇文章,可我觉得还不够好,总没写出来。
1946年秋天费米介绍我跟着艾里逊(Allison)教授做核物理实验。我在实验室做了差不多20个月的研究工作。1947年我曾经写信给黄昆,他那时候在英国读研究生,我的信中用了“希望破灭”。因为我在艾里逊实验室做得不成功,不成功的主要原因是我这人天生不是做实验物理的,动手不行,常常在实验闯祸,没有这方面的天分。
回想起来,那一年我自己找了四个理论题目,第一个是昂萨格(Onsager,编者注:美国物理化学家,1976年去世)关于伊辛模型(Ising Model)的文章,这是当时有名的统计力学题目。第二个是布洛赫(Felix Bloch,编者注:瑞士物理学家,1952年诺贝尔物理学奖获得者)关于自旋波(Spin Wave)的文章,也是有名的统计力学题目。第三个题目是规范不变。
这是我自己想出来的发展方向,但弄了几个礼拜无果而终。研究中找题目感到沮丧,是极普遍的现象,所有研究生差不多都有过一些沮丧。不过大家不要因为沮丧就觉得没有希望,不是你一个人,所有研究生都有这个问题。
前三个题目做来做去都没有结果,第四个题目是核反应中的角分布问题。这一问题与对称有密切关系,我就想到从吴大猷先生那学来的群论分析“物理规律旋转不变”的意义。1948年我得到结果就写了一篇很短的文章,泰勒很喜欢,主动来找我,他说文章很好,为什么不把它稍微变长一点,增加一点材料,可以接受这篇文章做我的博士论文。我决定接受泰勒建议的时候,如释重负。
我在芝加哥大学的两年半时间,自己找了四个题目,只有第四个有所发展,前三个费很大劲,没有结果。第四个题目是关于群论的,走到这个领域我非常兴奋,因为那时很少人对把“对称”用在核物理中感兴趣,我走进去了,所以很快占领一个新的领域。
我因此得出一个很重要的结论:一个人最好在研究开始的时候,进入一个新领域,到一个旧领域当然也可以,可是就像挖金矿一样,挖新矿容易出成果,如果一个地方人家已经挖了五年,要想再挖出新矿,就比较困难。
我在芝加哥大学还有一个非常重要的经历,就是与邓稼先的交往。邓稼先是我的中学同学,比我低两班,后来在西南联大,他也是物理系,因为我跳了一级,所以他比我低了三班。我到美国后,没过几年他也来普渡大学读书。1949年夏天他从普渡大学到芝加哥,我与他、还有我弟弟租了一个公寓,住在一起。他第二年取得博士学位后回国,50年代带领28个刚刚获得学士学位的物理系年轻学生研究制造原子弹,对中国原子弹和氢弹发展作出绝对性贡献,成为“两弹元勋”。
为爱留在普林斯顿 开始学术最有成果的17年
我认为所有研究工作多多少少要经过三步曲:兴趣--准备工作--新的突破点
1948年我在芝加哥大学获博士学位,留校教书。1949年就去了普林斯顿大学,当时最红的理论物理题目是“重整化”,在普林斯顿有很多人做这方面的研究,所以我要去普林斯顿。 本来想在普林斯顿呆一年就回芝加哥大学,但在普林斯顿碰见了我以前高中教过的学生(编者注:杨振宁在国立西南联合大学附属中学任数学老师),叫杜致礼(编者注:1927年出生,其父杜聿明,系国民党高级将领),她当时在卫斯里学院,我们偶然看见就交了朋友(编者注:1949年圣诞节,两人在普林斯顿中餐馆“茶园餐厅”邂逅),俩人恋爱了。那时在恋爱,觉得不应该回到芝加哥,所以就留下来,一呆就是17年。
普林斯顿的研究所不大,没有学生,大概有20个教授,四五个研究领域,一二百个博士后和访问学者,是一个纯研究性的象牙之塔,非常成功。
我到研究所的时候,那里大师云集。爱因斯坦刚刚退休,我们年轻人没有人去骚扰,都很尊敬他。有一天我带着大儿子在路上看见他,就照了一张照片,我自己从来没有与爱因斯坦合过照。
在研究所是完全放任的政策,每个人的消息都很灵通,自己找自己的合作者,这种方式到现在已经维持了七八十年,非常成功。我在研究所的主要兴趣是核物理。
1949年11月初的一天,在往返于普林斯顿大学与研究所之间的街车上,Luttinger(编者注:研究所的一名博士后)偶尔和我谈及伊辛模型,Luttinger说,考夫曼(Bruria_Kaufman,编者注:女物理学家,昂萨格的学生)已经把昂萨格的方法简化,因而可以通过2n个一系列“反厄米特矩阵”搞清楚。我对这种表象了解得很多,所以很快就理解了“昂萨格-考夫曼”方法。一回到研究所,我就搁置原来的工作,根据我在1947年关于这一问题的经验,再加上新的元素和观念,一两个小时后就完全弄明白,推导出“昂萨格-考夫曼”解法的基本步骤。
我觉得昂萨格还没有做完,于是就继续算下去,并得到最终公式。这份成果发表后,物理学界很多人非常注意我,可以说这是第一次。因为我把一个很复杂的计算变成很简单的公式,在芝加哥大学自己找的第一个题目开花结果。
此次研究的经验是什么呢?研究是一个三步曲:第一步是兴趣,我跟从王竹溪先生学习,使我对统计力学发生兴趣;在芝加哥大学的时候去研究这个问题,可以说是准备工作,准备工作不成功,也不稀奇,通常的研究都要经过不成功的准备工作;到最后突然出现一个新突破点,比如有了新的看法,与准备工作结合在一起,就开花结果。我认为所有研究工作多多少少要经过这三步。
我在芝加哥大学感兴趣的另一个题目是“规范不变”。1953到1954年我到布鲁克海文国家实验室(Brookhaven National Laboratory)访问,同办公室一位年轻人米尔斯(Robert Mills)谈话,很自然讲起来我对“规范不变”的不成功研究,我们讨论两天以后,决定再加两项进行运算,结果越算越简单。我们知道挖到宝藏了!
我把运算结果写成一篇文章寄给《物理评论》(Physical Review),变成我一生中最重要的工作,因为它把电磁学结构很美妙的进行了推广。电磁学结构是物理的一个中心,今天所有手机、电视、无线电都要用这个方程式。1954年文章发表后,并没有被大家注意,后来学者引进“对称破缺”观点,才大大发展了这一问题,成为标准模型。
通过这件事我又得到一个教训,物理学中的难题往往不能一举完全解决,如果把其中一部分解决,很可能为最后解决办法提供重要的中间一环。另外,与别人讨论往往是十分有用的研究方法。
1955到1956年我转而研究另外一个问题,θ与τ。θ是当时发现的衰变成2个π的粒子,τ是另外一个粒子,衰变成3个π。一方面发现θ跟τ有同样的质量、寿命,而通常2个不同粒子的质量比差很多,几倍、几十倍甚至几千倍。所以这两个粒子可能根本就是一个粒子,粒子有时候变成2个π,有时候变成3个π,同一东西变成两种不同的是常有现象。可是,另外一方面,存在宇称守恒定律,θ与τ不可能是同一个离子,因为根据此定律,2个π的“宇称”是+1,而3个π的“宇称”是-1,如果θ与τ是同一粒子,那么它既能衰变成+1的宇称,又能衰变成-1的宇称,宇称就不守恒了,违反了基本原理。当时就分成两派,一派说θ与τ是一回事,一派说θ与τ绝对不可能是一回事,当时很多文章要想解决这个问题,理论与实验都没有能够成功。
1956年夏天我和李政道合作,检查宇称是不是真正守恒,做了3个星期的多种计算后,我们很惊讶地发现,所有过去的β衰变试验中并没有任何宇称绝对守恒的根据。好几百个β衰变试验一致认为证明了宇称守恒,但这些结论都是不对的,我们从而提出怎么样做实验能够测定β衰变中宇称不守恒。这些实验比以前实验要稍微复杂一点,提出来以后学生都不肯做,第一,这些实验都不简单,他们说不值得去做;第二,没有人相信宇称是不守恒的。
只有吴健雄(编者注:美籍华裔女物理学家,有“东方居里夫人”之称,1997年去世)愿意去做这个实验,她认为这是一个基本的现象,既然还没有实验证明,那就应该去研究。吴健雄与其他专家合作,在华盛顿做了半年实验,得出结论在β衰变中宇称是不守恒的。结论出来以后震惊了整个物理学界。后来更多实验证明,不止是β衰变,在所有的相互作用中宇称都是不守恒的,也就是说左右不完全对称。
1997年吴健雄去世,我曾经写过这么一段话,“吴健雄的工作以精准著称于世,但是她的成功还有更重要的原因:1956年大家不肯做测试宇称守恒的实验,为什么她肯去做此困难的工作呢?因为她独具慧眼,认为宇称守恒即使不被推翻,此一基本定律也应被测试。这是她过人之处。”吴健雄自己曾说,永远不要把所谓不言自明的定律视为必然。
1949年到1966年是我一生研究工作最有成果的17年。1966年我离开普林斯顿,离开这样一个象牙之塔是极不容易的决定,后来常常有人问我,后不后悔离开,我后来说纽约州立大学石溪分校是新创建的大学,帮助一所新的大学变成一个好的研究性大学是一件很有意义事情,可以说这是我的一个重要转折。
我刚才讲了这么多,基本上就是把我过去的研究经历归纳一下,得出一些结论,也许这些结论对在座的年轻人会有些用处,谢谢。
中科大授予诺贝尔奖得主特霍夫特名誉博士学位
人民网 04-07-28 08:28人民网合肥7月27日电 记者何聪报道:7月27日下午,特霍夫特(G't Hooft)教授名誉博士授予仪式暨学术报告会在科大东区师生活动中心隆重举行。校领导朱清时、许武、李定出席仪式,理学院、研究生院等有关领导以及300多名师生参加了授予仪式和学术报告会。仪式由副校长侯建国院士主持。校长朱清时院士向特霍夫特颁发了名誉博士学位证书并发表了热情洋溢的讲话。这是继第三世界科学院院士、已故巴基斯坦物理学家、诺贝尔物理学奖获得者萨拉姆教授和美籍华裔物理学家、诺贝尔物理学奖得主丁肇中教授之后,中国科大授予的第三个名誉博士学位。
朱清时校长在致辞中高度评价了特霍夫特教授对现代物理学发展的杰出贡献。他说,特霍夫特教授在Yang-Mills规范场理论的工作为基本粒子的理论依据(标准模型)奠定了基础。“标准模型”被认为是科学史上堪与牛顿的引力理论媲美的瑰宝。值得注意的是,特霍夫特教授几乎所有工作都是在他的母国荷兰做出来的,Yang-Mills规范理论的工作是他在荷兰读研究生时做出来的。荷兰在欧洲属中等国家,在特霍夫特教授等的努力,该国对自然科学的贡献,得到世界科学界的高度尊重。特霍夫特教授致力于科学研究、奉献母国的精神对中国科学家是极大的鼓励,是我们学习的典范。中国科大一贯致力于基础研究,努力在国际前沿的一些重要领域有一席之地,已在量子通讯、纳米科学等领域取得了一些重要成果。我校授予特霍夫特教授名誉博士学位是一件十分有意义的事件,特霍夫特教授的来访并和我校同行的交流对于我们发展、壮大相关学科有很大帮助。
特霍夫特教授在仪式上讲话。他说,非常荣幸来到中国,特别是杨振宁先生的故乡,杨振宁先生的工作对我的影响很大,如果没有杨振宁先生就没有“标准模型”。非常感谢中国科技大学对我的厚爱,接受中国科技大学授予的名誉博士学位并在科大做学术报告,对我来说,是极高的荣誉。
特霍夫特教授1946年7月出生,现任荷兰Utrecht大学终身教授,著名物理学家。他对现代物理学的发展,特别是对于量子非阿贝尔规范理论的重整化的证明做出了杰出的贡献,他的工作为基本粒子的理论基础——粒子物理的标准模型——奠定了基础。他因此和导师M.Veltman荣获1999年度诺贝尔物理学奖。
此外,特霍夫特教授在非微扰场论和量子引力等方面也做了许多突破性的工作。他关于量子引力理论中的全息性原理被同行认为是一个新的革命性的思想,近年来成为弦理论和黑洞物理的中心课题之一。
近年来,中国科学技术大学的同行专家在特霍夫特教授所开创的领域里开展了一些列深入研究,并与特霍夫特教授保持了较为密切的学术交流。为进一步加强学术交流,促进科学研究事业的深入发展,依据《国务院学位委员会关于授予国外有关人士名誉博士学位暂行规定》,著名物理学家杨振宁教授、谷超豪院士、赵光达院士、朱清时院士、侯建国院士等一致写信推荐授予特霍夫特教授中国科学技术大学名誉博士学位,经中国科技大学学位委员会全体会议审议,国务院学位委员会通讯投票通过,决定授予特霍夫特教授中国科技大学名誉博士学位。
受聘仪式结束后,特霍夫特教授作了题为《探索自然规律的基本原理:我们从黑洞理论中能学到什么?》的学术报告,并与师生进行了交流。
受聘仪式前,朱清时、许武、侯建国、李定会见了特霍夫特教授。在校期间,特霍夫特教授还与理学院吴泳时、阎沐霖、胡森教授就黑洞物理理论问题进行了深入的学术讨论和交流,并参观了科大校园和相关实验室。
徐一鸿心中永远的痛
2009-09-26 18:55 徐一鸿当年没有计算Yang-Mills场, 是他心中永远的痛
从转动和空间反射这些可以感觉到的对称性开始,物理学家表述越来越多的对称性,到时间反演对称性,甚至我们感觉不到的规范对称性。但是几本的概念和动机始终是没有变的,基础物理学家们始终坚信:上帝设计设个世界的时候是以对称性为基础的。是这样的吗?你问我?我不知道,但是我可以告诉你的是,我能够感觉到是这样的,因为这样是美的,尽管我解释不了为什么对称就是美。
Einstein毕生精力都用在同一场论上,而对称性和重正化是场论的两个基本原则,可以说不能重正化的场论都不是最后的选择,这让我想起了2004年的Nobel Prize,David J. Gross, H. David Politzer, Frank Wilczek由于他们发现了强相互作用里面的渐进自由而得到炸弹奖,这是一个十分重要的工作,可以说是挽救了场论,
说到这里,不得不提到一个华人,名字叫Anthony Zee,中文名叫徐一鸿,UCSB的Kavli Insititute of Theoretical Physics的终生教授,1972年也就是上面三个人发表他们的得炸弹奖的论文时,他们文章是7月份发表的,A.Zee在5月份发表了一篇文章,里面他计算了除了Yang-Mills场以外的所有场的重正化都计算过了,没有得到渐进自由,也就是说随着能量越来越高,耦合强度越来越高,而渐进自由是指着时候耦合强度越来越小,趋近于零,A.Zee在文中非常sad的说到场论没有渐进自由,但是很不幸,那三个人计算了非阿贝尔规范场的重正化得到了渐进自由,记得我们当年上场论课的时候,当时青哥告诉我们叫我们去问问A.Zee为什么当年没有计算Yang-Mills场,估计这是他心中永远的痛:)
当时A.Zee刚好博士毕业两年,刚刚拿到洛克菲勒大学的教职,而且刚刚结了婚,计算了完了那篇文章,他正准备计算Yang-Mills场,他发现“在1972-1973年的那个冬天,如闻惊雷一样,我听到令人过电的消息”(他自己写道)那几个人找到了那个盼望已久的“自由”。我猜他当时的心情肯定不好受,虽然Yang-Mills场的重正化不好弄,但是至少他那时候已经哈佛大学理论物理博士毕业,日子肯定比H. David Politzer和Frank Wilczek好过, 他们两个还为了让别人肯定他们的工作而到处奔波。
场论方面数一数二的牛人
A.Zee也属于场论方面数一数二的牛人,当初在Princeton当教授时Witten当他助教,据说他当时计算了除非阿贝尔规范场以外的所有“贝塔"函数,如果当初再多算一个就发现QCD渐进自由了,那诺奖就没Gross他们什么事儿了,真是生不逢时啊。
徐一鸿讲演,http://www.youtube.com/
2004年诺贝尔物理学奖: 最郁闷的两个人
每年的诺贝尔获奖名单公布以后,获奖者当然高兴得不得了,但是也一定有人因为错过了发现的机会而扼腕长叹、顿足仰天。
2004年也不例外。我所知道的就有两位物理学家悔得肠子发青。一位是特霍夫特,一位是华裔美国物理学家徐一鸿。徐一鸿在1972年春天就想到了“渐近自由”,但是这种想法在那时是太出格了,他自己都认为他的想法荒诞到好像是在说:“如果他的伯母是一个男人的话,她会怎么样呢?” 因此他没有敢再往下想。
最可惜的是荷兰物理学家特霍夫特。在1972年春天马赛一次会议上,他对德国物理学家西曼尼说,他可以证明“渐近自由”符合现有的理论;西曼克觉得难以置信说:“倘若你是对的,那么你应该马上发表这一结果,因为这会十分重要!”可惜特霍夫特当时忙于进行另外一个还没有结束的研究,没有听从西曼尼的建议。到1973年格罗斯、维尔切克和波利策发表他们的发现以后,特霍夫特真是后悔得想自己把自己狠狠揍一顿!
杨振宁:中国教育缺乏“渗透”型学法 http://www.stdaily.com 2012年04月25日 来源: 中国科学报 作者: 陈彬
“知之为知之,不知为不知,是知也”的传统教育哲学有其合理之处,但并不适用于每个时代。事实上,很多知识不是按部就班,而是在不断地实践和失败中,不知不觉学会的。我更愿意称这种方法为“渗透”型学法,这是中国传统教育不喜欢的,却是非常必要的。
■本报记者 陈彬
“知之为知之,不知为不知,是知也。”这句出自《论语》中的经典论述,千百年来一直是中国传统教育理论中对于学习态度的经典论述。但在4月17日,中国农业大学举办的名家论坛上,著名物理学家、诺贝尔奖获得者杨振宁对此却提出了反思。
见解不对不要紧
当天,杨振宁以《我的学习与研究经历》为题,向到场师生讲述了他几十年的求学与研究生涯。在演讲中,杨振宁提到,1946年初他进入芝加哥大学,成为该校物理系的博士生。而在芝加哥大学的经历让他对中西方的教育产生了反思。
“芝加哥大学汇集了一大批杰出的学者,其中我接触比较多的便是爱德华·特勒教授。”杨振宁说,特勒后因发现氢弹的制造原理被称为”氢弹之父”。而在他看来,特勒在研究物理学时,有一个特点,那就是他有许多直觉的见解。“这些见解不一定都是对的,甚至恐怕90%是错的。不过每次和别人交谈时,他从不怕他讲的见解可能是错的,这给了我很深的印象。”
杨振宁表示,中国传统教育观念中,“知之为知之,不知为不知,是知也”的表述,要求学习者在发表言论之前,必须明确区分知道的事情和不知道的事情,要想得清清楚楚,这才是真正学习。这种传统教育哲学有其合理之处,但并不适用于每个时代。“事实上,很多知识不是这么学的。比如幼儿学习说话,这一过程就不是按部就班,而是在不断地实践和失败中,不知不觉学会的。我更愿意称这种方法为‘渗透’型学法,这是中国传统教育不喜欢的,却是非常必要的。”
杨振宁强调,即使是在当今,中西传统教育观念对教学的影响依然明显。“西方教育从不教学生‘知之为知之’,而是允许学生在‘乱七八糟’的胡思乱想中学会知识。和我共事的西方学者有一个共同特点,他们在讨论的时候没有把问题想得很清楚的习惯,但这没有阻止他们做出非常重要的工作。这一现象值得反思。”
要有骨头,还要有血肉
在赴芝加哥大学求学之前,杨振宁在西南联合大学学习,比较芝加哥大学与西南联大的不同时,杨振宁说,在西南联大求学时,他所采用的学习方法主要是推演法:即由理论原理推演到物理现象。而在芝加哥大学则正好相反:从新的现象开始,通过对现象的描述归纳理论。
“如果和既有理论相符合,固然很好;如果不符合,就代表着固有理论存在错误,需要修改。这更是一件‘好事’。”杨振宁说,渐渐地,他了解到了这种方法的好处:归纳法的起点是物理现象。从这个方向出现,不易陷入形式化的泥坑。
回想起在芝加哥大学的求学经历,杨振宁坦言自己学到的不仅有一般书本上的知识,尤其重要的是方法与方向。通过当时芝加哥大学研究的气氛,他接触到最可能有发展的研究方向。“我常常想,我是很幸运的。在联大我有了一个扎实的根基,学了推演法。到了芝加哥受到新的启发,学了归纳法。掌握了一些新的研究方向。两个地方的教育都对我以后的工作有决定性的作用。”他说。
1971年,杨振宁在考察了多所国内大学后,曾写过一篇文章,其中提到,国内的大学所教的课程往往是非常深的。有所谓“四大力学”。每一个大学物理系的学生都要花很长的时间去念这四门很深的理论课。“四大力学”是不是重要的呢?当然是重要的。没有人能否认“四大力学”是物理学的骨干。不过,物理学不单只是骨干。只有骨干的物理学是一个骷髅,不是活的。物理学需要有骨头,还需要有血、有肉。有骨头又有血肉的物理学,才是活的物理学。
“物理学的学习不但需要对知识的掌握,更要有正确的研究方法和研究态度。对于几十年前我所提出的这一问题,目前在国内大学有了一定程度的改进,但并没有完全解决,要改变现状,还需要我们继续努力。”杨振宁说。 (中国科技网)
杨振宁谈科普
国内作者缺乏扎实态度和许多名人完全不同,杨振宁说话不讲客套,在其发言环节,他尽显科学家的研究姿态,解剖起国内的科普创作来。
杨振宁的话语甚至有些激烈,他说,现在整个世界对科技的发展越来越重视,但国内对于向民众介绍各个领域、各个层次科学的工作,做得非常不够。“讲一句不客气的话,多半科普文章不忍卒读,作者没有扎实态度,而往往是投机取巧的居多。”
杨振宁尤其强调,科普写作扎实态度的至关重要。他甚至以科学家人物传记做为突破口,为年轻人进行了现场普及。杨振宁说,爱因斯坦的传记写作者至少有30多位,但只有一位作者的传记被公认为最出色,这位作者曾经是杨振宁的同学,也是一位物理工作者,叫派斯(Abraham Pais)。从20多岁起,派斯就想写爱因斯坦,每次和爱因斯坦接触,他都会把对方讲话的内容记录下来。杨振宁说,派斯累积了近20年,直到上世纪80年代,由他撰写的《爱因斯坦传》(Subtle is the Lord — The science and the life of Albert Einstein)才面世。
杨振宁认为,事实上,科学研究前沿的很多问题是非常有意思的,要想真正做出来卓越的工作,需要对有意思的事情发生浓厚的兴趣。“我一直说,做一个工作要有三部曲。第一步,要对这个问题发生浓厚的兴趣。第二步,要做一个长期的思考和努力,这个长期的努力常常是不成功的,甚至使你自己非常沮丧。第三步,100年以前有一个大数学家分析过,他说你做了很复杂的努力,不出结果甚至很沮丧的时候,你常常不可避免地要休息一下子。” (来源是亨利·庞加莱(Jules Henri Poincaré)的The Foundations of Science: Science and Hypothesis, the Value of Science, Science and Method -- I turned my attention to the study of some arithmetical questions apparently without much success and without a suspicion of any connection with my preceding researches. Disgusted with my failure, I went to spend a few days at the seaside and thought of something else. One morning, walking on the bluff, the idea came to me, with just the same characteristics of brevity, suddenness and immediate certainty, that the arithmetic transformations of indefinite ternary quadratic forms were identical with those of non-Euclidian geometry.)
杨振宁:《易经》对中华文化的影响
——在人民大会堂举行的“2004文化高峰论坛”上所做的报告
杨振宁
睿智的杨振宁先生
[编者按]这是杨振宁先生2004年9月3日在人民大会堂举行的“2004文化高峰论坛”上所做题为“《易经》对中华文化的影响”的报告。杨振宁先生是华人科学家的骄傲,是1957年诺贝尔物理学奖得主,他在这次报告中对《易经》的批评非常尖锐,报告在海内外的华人圈中引起巨大反响,尽管杨振宁声明自己并无攻击中国传统文化之心,但还是引起了来自广泛途径的持久的激烈批评,在国内学术界引起很大的争论。今日将报告全文转摘在此,供各位网友欣赏。
杨振宁:《易经》对中华文化的影响
各位女士,各位先生,方才对我的介绍有一点点需要更正的地方:我在美国纽约州立大学已经退休了,我现在是北京清华大学的教授与香港中文大学的教授。
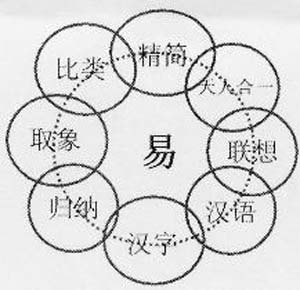
我的题目是《《易经》对中华文化的影响》,以下几十分钟要讨论许多观念:精简、比类、天人合一,联想,取象,汉语汉字之形成,归纳等。这么多观念很短时间不能讲得清楚,主要讨论的集中于三点。 (附图一)
第一《易经》影响了中华文化中的思维方式,而这个影响是近代科学没有在中国萌芽的重要原因之一。这也是我所以对于《易经》发生了兴趣。
第二《易经》是汉语成为单音语言的原因之一。
第三《易经》影响了中华文化的审美观念。
我是研究物理学的,没有研究过历史学、考古学、语言学、语音学、美学、哲学等等。可是对于中国文化的成因,我近年来发生了兴趣,所以大胆的今天在这个场合跟大家谈谈我自己的一些想法。
《易经》大家知道是中国非常古老的一个文献,据说是夏朝已经有了最早的《易经》叫连山,商朝有了比较晚一点的归藏,都失传了。我们现在所看见的《易经》是西周时候的周易。所以《易经》的孕育前后至少经过一千多年,这个结论我想是大家可以同意的。
《易经》里面64卦开始是乾卦和坤卦。如果问《易经》是怎么形成的,以下这个说法大家似乎可以接受:最早中国发展了占卜,因为要对占卜作系统性了解就发展了卦符,所有64卦都有卦符。乾就是六个连线,坤是六个断线。有了符以后还得有名与字。卦名有音,有音还不够,就有一个字。这前后发展的次序我不是研究考古学的,不过我想这个次序很可能多少是对的。
可是我们知道孕育《易经》的年代也正是汉语汉字开始形成的年代,是中华文化孕生的年代。这些卦是“象”,这是周易里面自己讲的,是浓缩了的观念,以卦符卦名将天、地、人的变迁分类为“象”。
上面这几句话可以说是用今天的语言来描述到底《易经》的精神是什么:浓缩化、分类化、抽象化、精简化、符号化是《易经》的精神。而这种精神我认为贯穿到了几千年以来中国文化里面每一个角落。
譬如分类精简,例子极多。今天大家知道中医的理论其中重要的一点就是把疾病与医药各分成阴阳、寒暖、表里,等类,用这个分类的观念做大前提发展中医理论。这是从《易经》的传统所遗留下来的。像这样的例子我们可以举很多。
一、近代科学没有在中国萌生的原因
近代科学为什么没有在中国萌生。已经有很多人讨论过了。归纳起来大概有五种道理:
第一,中国的传统是入世的,不是出世的。换句话就是比较注重实际的,不注重抽象的理论架构。
第二,科举制度。
第三,观念上认为技术不重要,认为是“奇技淫巧”。
第四,中国传统里面无推演式的思维方法。
第五,有天人合一的观念。
第四跟第五两点跟《易经》我认为都有密切的关系。
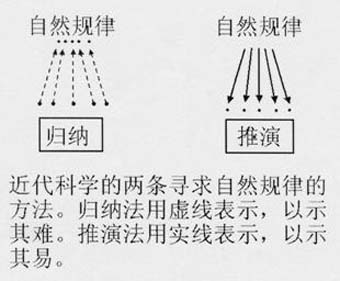
先讲第四点,关于推演与归纳两种思维方法。近代科学的思维方法见下图:(附图二)
归纳与推演都是近代科学中不可缺少的思维方法。为说明此点让我们看一下Maxwell(1831-1879)创建Maxwell方程的历史。
Maxwell是十九世纪最伟大的物理学家。他在十九世纪中叶写了三篇论文,奠定了电磁波的准确结构,从而改变了人类的历史。二十世纪所发展出来的无线电,电视,网络通讯等等,统统都基于Maxwell方程式。他是怎样得到此划时代的结果呢?
他的第一篇文章里面用的是归纳法,里面有这样一段话:
“我们必须认识到互相类似的物理学分支。就是说物理学中有不同的分支,可是他们的结构可以相互映证。”
他用这个观念来研究怎样写出电磁学方程式,以流体力学的一些方程式为蓝本。这种研究方法遵循了归纳法的精神。
几年以后,在第三篇文章中他把用归纳法猜出的电磁方程式,运用推演法而得出新结论:这些方程式显示电磁可以以波的形式传播,其波速与当时已知的光速相符,所以“光即是电磁波”,这是划时代的推测,催生了二十世纪的科技发展与人类今天的生活方式。
上面的故事清楚地显示归纳与推演二者同时是近代科学的基本思维方法。
中华传统文化的一大特色是有归纳法,可是没有推演法。其中归纳法的来源是什么?
“易者象也”,“圣人立象以尽意”,“取象比类”,“观物取象”。
都是贯穿《易经》的精神。都是归纳法,是向上求整体“象”的方法。
可是中华文化没有发展出推演法。我们怎么可以证明此欠缺呢?请看徐光启的一些话:徐光启(1562-1633)是明朝末年一个大臣,而且是一个大学者。大家知道他是最早与利玛窦合作翻译欧几里德的几何原本的人,翻译了前六章。他们翻译的原版,现在在国内还有几本,我曾经在北京图书馆去请他们给我看过一本。
欧几里德的几何学是人类历史上一个大贡献,第一次把推演法规律化,其影响不可以道里计。后来牛顿写了Principia Mathematica。如果你翻一下此书你就会发现他写的方法完全是照着欧几里德几何原本方法,是由公理,定理,然后到证明等等。它是照抄欧几里德的推演法的形式。不幸的是徐光启翻译几何原本的时候虽早,(那时牛顿还没有出生),可是这翻译有将近三百多年在中国没有发生应该有的影响。
徐光启在翻译了以后,了解到推演法一个特点就是“欲前后更置之不可得。”
就是一条一条推论不能次序颠倒。这跟中国传统不一样。中国传统对于逻辑不注意,说理次序不注意,要读者自己体会出来最后的结论。徐光启又有这样几句很有名的话:
似至晦,实至明,
似至繁,实至简,
似至难,实至易。
这也是推演法的特点。懂了推演法的精神以后就知道推演其实比归纳容易。请参阅图二。
下面要讲上述第五点,关于“天人合一”的观念。
“天人一物”,“理一分殊”,“内外一理”,起源于易经每一卦都包含天道地道与人道在内,天的规律跟人世的规律是一回事。
我们知道王阳明格竹子,是要用人世间的“理”追求自然界的“理”,这样当然格不出近代科学。近代科学一个特点就是要摆脱掉天人合一这个观念,承认人世间有人世间的规律,有人世间复杂的现象,自然界有自然界的规律与自然界的复杂现象,这两者是两回事,不能把它合在一起。
当然我讲这句话会使得很多人觉得,尤其是研究中国哲学的人觉得我对于中国的传统哲学攻击得太厉害了。我完全没有攻击的意思。天人合一的内涵绝不止内外一理,还有更重要的“天人和谐”。天人和谐对于中国的传统影响极大。而且从今天的世界现状讲起来,我们可以问,摒弃天人合一而完全用西方的办法发展下去是否将要有天人对立的现象。这是一个非常重要的题目,不过不在我今天所能够讨论的范围之内。
二、汉语汉字的成因
世界上原始语言与成熟语言几乎都是复音的,单音的语言是仅有的。我不晓得任何一个别的成熟的语言是像汉语这样单音的。近年考古学家发现一万六千年以前江西的居民已经采集野生稻为主要的粮食。所以在一万多年以前已经开始形成了中华文化。我们可以相信他们已经有语言,我们也有理由可以假设,这些我们的祖先所用的语言是复音的。那么后来怎么变成单音的汉语呢?
从复音的汉语变成单音的汉语这中间一定有一个很长的过程,而且一定有它的道理,因为这是十分独特的事情。
我的一个大胆的假设是:这变化是受了易经的影响。卦名是单音的。乾、坤,……都是单音的。是统治者用的,是神秘的,有重大影响的,念起来有份量的。久之就形成了一个重视单音符号的价值观,而影响后来整个汉语的发展。在座有语言学的专家,我这个讲法是很大胆的,希望不被语言学家批评得体无完肤。我们看元、亨、利、贞、吉、凶、阴、阳、日、月、天、地,这些有声有色,有份量的,讲出来有影响的单音字对于整个语言文字的发展当然产生重要的影响,所以我刚才说我猜想汉语、汉字所以变成单音的语言文字与《易经》有密切关系。
三、中华文化的审美观
《易经》的浓缩化,分类化,抽象化,精简化,符号化的精神对中华文化的影响极深又极广。下面我简单讨论它对汉语、汉文法、文学、艺术、书法等的影响。
英文“Word”,通常翻译为字。这不恰当。应翻译为词,是一个或好几个字构成的。比如“现代”,比如“所以”,都是两个字的词。词可以是一个,两个或更多字所组成的,可是绝大多数是一个或者两个字的,不太有三个字以上的词。多半的三个字或以上的词都是复词,或是音译的词。前者例如“外祖父”,“洞庭湖”,后者例如“成吉思汗”。
19世纪开始翻译元素名字的时候也只用一个字,氧、硫、镭,这些在英文里面都是复音的,在中国翻译都变成一个单音的词。为什么这样吝啬呢?我认为在中华文化形成时代,在汉语形成时代,受了易经的卦名的影响,发展出来了精简为美,浓缩为美的深层观念。此审美观影响了词的形成。
世界所有的语言都有共同的深层文法,然后在此深层文法之上,不同的语系各自发展,这是Chomsky的一个大发现。比较不同的语言就会发现每一种语言都有名词,动词,形容词、介词等等。汉语亦然。可是汉语的一大特点就是极少用介词。例如不说“我的父亲”而说“我父亲”;不说“慢慢地跑”而说“慢慢跑”,把介词省略掉了。所以西方人说中文是电报式的文字,尤其是古文。好的古文确实是极美的文学。美的原因之一就是古文不遵循通常文法的发展方式,而力求用最少的词表达出最多的意思。这种审美观念应是易经的浓缩化精简化的申延。
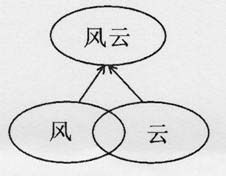
联想在世界任何文学之中都占重要的位置,而在汉文文学之中占有特别重要的位置,因为汉文中的词既常常建构于数个单音的字,就往往是根据联想而形成的。譬如风气,风云,风流,风景,风光,风雨,风俗都是联想形成的词。风云一词的形成可用下图表示:(附图三)
这种词的结构更进一步促使汉文学演化成联想的文学,“云想衣裳花想容”,“秦时明月汉时关”就都是升华了的联想。
中华传统绘画所追求的意境与西方传统绘画完全不同,是“观物取象”的象,不是照像的像;是精神的象,不是形似的像;是天人合一的象,不是歌颂自然的像。我认为这种思维精神是从易经来的。
至于说易经对书法的影响,更是非常清楚了。书法在传统的中华文化中占极重要的位置,是其它文化所没有的。
而书法显然跟《易经》的浓缩化、符号化、抽象化的精神有直接关系。我一个好朋友书法家、雕塑家、文学家、文学评论家熊秉明在《中国书法理论体系》里面曾说中国文化的核心是哲学,中国文化核心的核心是书法,我所以完全同意他这句话,就是因为书法把《易经》的精神具体化了,现实化了。
2004年9月23日 定稿
(附图一)
(附图二)
(附图三)
杨振宁:在科学与玄学之间
11月20日,在博鳌亚洲论坛会议中心举办的新闻发布会上,杨振宁博士再次肯定了他在《2004文化高峰论坛》的说法。“很多人曾讨论过近代科学为何没在中国萌生,我觉得和《易经》有很大关系。”杨博士认为,中华文化有归纳法,可没有推演法。采取天人合一的哲学观念,是受《易经》的影响。 诺贝尔奖获得者杨振宁,在“2004文化高峰论坛”上指出,《易经》是近代科学没有在中国萌芽的罪魁祸首,在文化与科学界引起剧烈争论。 再度成为新闻焦点人物杨振宁作为在华人当中知名度最高的当代科学家之一,他的影响力并不局限于物理学界。像许多大科学家一样,他极为关注、热心参与社会事务,特别是与中国有关的事务。1971年夏天,在中美关系正常化的前夕,杨振宁即访问中国,成为第一位访问新中国的美籍科学家。从此他致力于中美科技、教育交流,并经常对中国时事发表评论。去年年初杨振宁回国定居后,更是成为新闻焦点人物。他在清华大学为低年级本科生上物理课,频频在各种场合发表演讲,都被广泛报道乃至引起争议。去年底传出了82岁的杨振宁与28岁翻译系硕士生结婚的消息,更是成为中文网上一个热门话题。
“苍苍白发对红妆”虽然让人津津乐道,却只配作为饭后谈资,而且风波会很快平息。“炮轰易经”才是杨振宁在2004年所做的最有意义、最有影响的一件事。
引来国学家、易学家的指责
2004年9月3日,杨振宁在北京人民大会堂“2004文化高峰论坛”上作题为《〈易经〉对中华文化的影响》的演讲,认为“《易经》影响了中华文化中的思维方式,而这个影响是近代科学没有在中国萌芽的重要原因之一”。一时舆论大哗,国学家、易学家们纷纷出来批评杨振宁不懂装懂、说外行话,甚至对杨振宁破口大骂。10月23日,在清华大学举办的“中国传统文化对中国科技发展的影响论坛”上,杨振宁再次阐明自己的观点并和与会者进行了激烈争论。
爱因斯坦早有说法
尽管中国古代对人类科技发展做出了很多重要贡献,但是为什么近代科学没有在中国萌芽?这个问题在科技史研究中被称为“李约瑟难题”。1953年爱因斯坦在致斯威泽的信中,曾经给出过一个答案:
“西方科学的发展是以两个伟大的成就为基础的:希腊哲学家(在欧几里得几何学中)发明了形式逻辑体系,以及(在文艺复兴时期)发现通过系统的实验有可能找出因果关系。在我看来,人们不必对中国圣贤没能做出这些进步感到惊讶。这些发现竟然被做出来了才是令人惊讶的。”
言下之意是,古代中国学者不懂得形式逻辑体系和实验验证,因此没能发展出近代科学并不令人惊讶。
为何咎归《易经》
杨振宁实际上给出了一个类似的答案,只不过他把原因进一步归结为《易经》的影响。他认为近代科学没有在中国产生的原因有5条,其中2条与《易经》的影响有关:中国传统里面只有归纳法而无推演法(即演绎法)的思维方法;“天人合一”的观念。归纳与推演都是近代科学中不可缺少的基本思维方法,但是贯穿《易经》的精神,都是归纳法,而没有推演法。近代科学的一个特点就是把自然规律与社会规律分开,而《易经》的“天人合一”观念却将天道、地道与人道混为一谈。
许多国学家在批评杨振宁时,甚至连杨振宁的意思都没有搞清楚。例如著名易学家、山东大学哲学系教授刘大钧批评杨振宁的演讲“有很多常识性错误”,并举例说:“众所周知,《周易》是最早的一部算卦的书,算卦的方法就是靠推演,举一反三,怎么能说没有推演呢?另外,《周易》是一本‘普世之书’。从这个角度,也是一种广义的‘推演’。”但杨振宁所说的推演法指的是逻辑推理,根据一些已成立的一般性命题严密地逐步推出较特殊的结论,例如在欧几里得几何中,由公理,定理,然后到证明等等。这显然和刘大钧说的周易算卦的推演完全不是一回事。
可见,杨振宁和爱因斯坦一样,把希腊哲学家发明的形式逻辑体系视为近代科学的源泉之一,并认为中国古代文化缺少这个源泉:“中国传统对于逻辑不注意,说理次序不注意,要读者自己体会出来最后的结论。”实际上,中国传统中不仅缺少合乎逻辑的严密推演法,也缺少合乎逻辑的严密归纳法。杨振宁认为《易经》的“取象比类”、“观物取象”的所谓归纳法,其实是在“天人合一”的神秘主义观念指导下的不合乎逻辑的类比法。例如:“枯杨生华,老夫得其女妻,无不利。”(枯萎的杨树生出新芽,老年男子娶了年龄可当其女儿的年轻女子为妻,没有不利的)、“枯杨生华,老妇得其士夫,无咎无誉。”(枯萎的杨树开花,老年女子嫁给年富力强的男子,没有祸害也不值得称道)。在“枯杨生华”和“老夫得其女妻”、“枯杨生华”和“老妇得其士夫”这种天道和人道之间只有模糊的相似性,并不存在任何合乎逻辑的必然关系,由此归纳出的“无不利”、“无咎无誉”的结论更是站不住脚的(可以举出无数的反例加以推翻)。这种“推演”无非是男尊女卑的社会观念的反映,或许还有一些生理上的道理,但是与逻辑推理无关。
中国传统的说理方式不具有逻辑性,是许多中外学者都已指出过的一个事实。但《易经》对这种非逻辑说理传统的影响有多大,是否是其源泉,是一个可以讨论的问题。杨振宁不过是对老学术问题提出了一些见解,为何引起如此大的风波?
科学与玄学之争的延续
狭隘民族主义与伪科学相结合的思潮在中国虽然不像十几年前那么流行,但是仍然大有市场。风水、占卜、命理、天人感应、巫术等与《易经》有着千丝万缕联系的传统迷信在死灰复燃的同时,又往往被披上迷人的科学外衣,甚至有人声称它们代表着“新科学”,至少也是“潜科学”、“类科学”。也有人论证《易经》是超前的科学著作,里面蕴涵着量子力学、相对论、计算机理论、遗传密码等许多重大科学发现。还有人要以《易经》指导科学研究,根据它提出的“太极原子模型”,推演出“太阳系有十四颗大行星”,或要用它预测气象变化。 杨振宁指出《易经》的思想和方法根本就与科学格格不入,甚至要为近代科学没有在中国产生承担罪责。虽然许多人做过类似的批评,有的批评要比杨振宁的演讲更严密、更尖锐、更全面、更有说服力。但是杨振宁作为人人敬仰的大物理学家登高一呼,其影响非同小可。特别是,杨振宁向来被视为具有极强的民族自尊心、热爱中华传统文化的海外华人,他的反戈一击,矛头直指被视为中华传统文化源泉之一的《易经》,更要让易学家们大为光火。这实际上是自20世纪初以来科学与玄学之争的延续,能够引起如此大的反响,也反映出当今中国科学与玄学、科学与伪科学、科学与反科学的争斗的激烈程度。由于杨振宁的加入,大大增加了科学一方的力量,算得上是他为中国科学的发展做出的一个大贡献。
摘自《人物》 方舟子文
杨振宁在2002年6月巴黎国际理论物理大会做报告的记述
“千古三旋律,循循谈笑中”是杨振宁先生的“归根”诗中的一句。作为一名普通的物理学工作者,我非常有幸目睹了这个诗句所指的重要事情。现在根据杨先生的有关文章(见参考文献[1]),以及我对此事的回忆和感受写下下面的文字,从而与大家分享从杨先生那里得到的珍贵教益和鼓舞。这也算是对2005年世界物理年活动的一点贡献。2002年6月22至27日,巴黎。国际理论物理大会在联合国教科文组织(UNESCO)的会议厅召开。在当代,这种覆盖物理学几乎所有分支的大会是很少的。这次会议可以说是在世纪之交人类对物理学的一个总结和展望。如果当时你在那里,你会经常在不同分支学科的报告中,听到同一个名字:杨(Yang)。你会听到如“杨-李零点”(Yang-Lee Zeros)和“杨-巴克斯特方程”(Yang-Baxter Equation)这样一些名词,而更多地会听到“杨-米尔斯理论”(Yang-Mills Theory)。当然,这个杨就是杨振宁。
在国际物理学界,并且在整个物理学史上,杨振宁(Chen Ning Yang或Frank Yang)永远是一个响亮的名字。
那次理论物理大会的压台戏是两位极重要的人物的历史性报告。一位是凝聚态物理大师安德森(P. W. Anderson)。另一位就是杨振宁。
在安德森的报告开始前,杨先生飘然来到会场,坐到第一排中间一个空位上,并习惯性地摆正话筒。杨先生身着白衬衫,步伐矫健,动作麻利。对于当代物理学的老将们来说,这个熟悉亲切的身影与二十世纪后半叶物理学的许多风云岁月密切相关。当时我在听众中,看到安德森和费希尔(Michael Fisher)向会议组织者金-嘉思廷(J. Zinn-Justin)指明杨先生的位置:“Frank is there”。费希尔是统计物理大师,将主持安德森和杨先生的报告。
我不知道与会者中有没有人曾在1956年的罗切斯特会议(Rochester Conference)上听三十多岁的杨振宁综述θ-τ之谜,或者有没有人1960年在乌特瑞特(Utrecht)听四十多岁的杨振宁讲非理想玻色(Bose)系统。不过我确实认识一位作大会报告的教授,知道他曾是参加1982年马哟拉纳(Majorana)暑期讲习班的学生。那是为庆祝杨振宁六十寿辰举办的规范作用(Gauge Interactions)讲习班,理论物理大师狄拉克(P. A. M. Dirac)、维格纳(E. Wigner)和特勒(E. Teller)都参加了。当时特勒在报告中呼吁他的最好的学生杨振宁应该得到第二次诺贝尔奖。而狄拉克和维格纳都是杨振宁学生时代佩服的物理学家。恐怕学生时代的杨振宁没有想到过几十年后他们会参加自己的生日祝寿。
我们还是回到巴黎会议。安德森的报告是“凝聚态物理五十年”,主要是回顾他五十年中对凝聚态物理的贡献。报告开始时,他先指出上一次这样全面的理论物理大会是1953年在日本。确实,我曾读到过著名物理学家费曼(Richard P. Feynman)和佩斯(A. Pais)的有关那次会议的回忆。安德森还回忆了会议期间他和杨振宁两家的交往,并展示了一些当时的照片。当时他和杨先生都带了夫人和孩子。江才健的“杨振宁传”上记述,那时持中华民国护照的杨夫人杜致礼和大儿子到台湾探亲后要回美国时遇到麻烦,正好先在日本与杨先生团聚。顺便提一下,巴黎会议结束后,记忆力过人的杨先生告诉我,安德森把自己的女儿当时的年龄说错了。
会议休息后,是大会的最后一个报告:杨振宁的“二十世纪理论物理的主题旋律:量子化,对称和相位因子”(“Thematic melodies of 20th century theoretical physics: quantization, symmetry and phase factor”)。主持人费希尔特别提醒大家:杨教授的第一篇科学论文发表在“化学物理杂志”(Journal of Chemical Physics)。虽然杨先生最著名的工作是在高能物理方面,可是在高能物理和统计物理两方面的贡献都是伟大的。作为统计物理学家的费希尔的意思大概是说杨先生的科学生涯始于统计物理。不过,从杨先生的论文目录可知(见参考文献[2]),其实杨先生的第一篇论文是数学论文,发表在“美国数学会通报”(Bulletin of American Mathematical Society)上,而费希尔说的那篇文章是杨先生的第三篇论文。这些都是杨先生在中国做学生时的工作。费希尔也提到当年杨先生对作为后生的他的慷慨帮助。他还提到杨先生刚刚度过八十大寿。然后很到位地说:“他要唱二十世纪物理学的主旋律(He is going to sing the thematic melodies of 20th century physics)”。因为安德森刚才提到1953年在日本的会议,杨先生在开始正式报告前告诉大家,那次会议的参加者中有十几位后来得到了诺贝尔奖。
杨先生的报告横跨一个世纪,与他的科学论文风格一致:优美简洁,浑然一体,抓住要点,含义深邃。像是一篇不朽的壮丽史诗。报告的主要内容已经作为一篇综述文章发表在“国际现代物理杂志”上(见参考文献[1])。为了与大家分享杨先生对物理的整体把握和精彩述评,以及由此传达的物理学的激动人心,下面我尝试把杨先生这篇文章的引言部分翻译成中文:
“人们说二十世纪是物理学的世纪。有充足的理由支持这个说法:人类自从祖先发现了火之后,在这个世纪里发现了第二个而且强得多的能源:核能。在这个世纪里,人类学会了操纵电子,从而创造了晶体管和现代计算机,改变了生产力和生活。在这个世纪里,人类学会了探测原子尺寸的结构,从而发现了核酸双螺旋这个解开生命奥秘的钥匙。在这个世纪里,人类挣脱了地球的束缚,在月球上跨出了最初的步伐。总而言之,在这个世纪里,人类在许多的前沿取得了前所未有的进步。而这些进步大多数是由物理学上的震撼人心的进展所带来的。
人们很难不对二十世纪物理学的巨大发展在人类历史上的决定性角色留下深刻的印象。但是虽然这些在人类历史上的角色是决定性的,它们却不代表二十世纪物理科学发展的真正辉煌。
二十世纪物理学的真正辉煌在于对重要的发源于人类文明之始的原初概念的加深理解:空间、时间、运动、能量、力。对于所有这些原初概念,我们的理解都发生了深刻的革命,而这些革命带来了一个更美、更微妙、更准确、更统一的对自然的描述。
近年来人们对于二十世纪物理学的详细历史有多方面的研究。我这里不去仔细探讨这些课题。我将做的是在这个历史里找到物理学发展的基调,整理出三条主线。这三条主线通过概念的发展持久地编织在一起,并以多种形式一次又一次地或单独或交织地再现,正如同交响乐的主题旋律一样。我们将看到这三个旋律一起决定了二十世纪物理学的主要发展的音调和味道。”
然后杨先生的阐述分四部分。下面我对此介绍一下大概内容(详见参考文献[1])。
一、量子化。这是第一个主旋律。杨先生认为量子力学是人类历史上最伟大的思想革命(intellectual revolutions)之一。杨先生特别讲了在量子力学的诞生过程中,它的创造者们当时的既有希望又有绝望的深刻感受。杨先生精彩地引述了量子力学的创造者们在苦苦求索时发出的肺腑之言,以及奥本海默(J. R. Oppenheimer)的一段拨动心弦的评论。
我们知道,奥本海默二十年代曾在欧洲跟随量子力学的创造者们。他在1947年至1966年任普林斯顿高等研究所所长(Institute for Advanced Study,Princeton)。而杨先生1949年至1966年在该研究所工作。
二、对称性。这是第二个主旋律。杨先生阐述的内容大概如下。这个主旋律从爱因斯坦(A. Einstein)的狭义相对论,特别是闵科夫斯基(H. Minkowski)对它的四维描述开始。爱因斯坦对这个时空对称性的推广最终导出了广义相对论。对称性这个旋律的另一变奏则是在量子力学里。通过量子力学,人们意识到,原子物理中的量子数与对称性有深刻的关系,而群论正是关于对称的合适的数学工具。后来通过核物理和粒子物理的发展,对称性和群论成了物理学中的一个主导性主题。
我们知道,杨先生正是这个主题的高峰期的一位领袖。杨先生在西南联大读书时,就在统计物理和对称性两方面打下优秀的基础。后来,杨先生在对称性研究上的特长正好与粒子物理发展的需要相契合。正如杨先生曾经说过的,他和他的同事与粒子物理一起成长。
三、相位因子。这是第三个主旋律。杨先生首先引述了狄拉克七十岁时说的一段关于量子力学里的相位因子的重要性的论述。然后,杨先生讲述了最初相位因子是如何被发现的。杨先生告诉我们, 1922年,薛定谔(E. Schrodinger)在创立正式的量子力学前就发现,通过加入一个虚数单位,魏尔(H. Weyl)的规范(gauge)或伸展(stretch)因子就变成相位因子。后来福克(Vladimir Fock)和弗里茨·伦敦(Fritz London)也作过有关的探讨。再后来魏尔自己也更正失误,创立了正确的电磁规范理论,从而“规范”的涵义更正为相位。然而相位因子的重要性沉睡了几十年。
事实上,这段曲折历史的发掘是杨先生对物理学史研究的重要贡献。
四、展开。杨先生指出,三个主旋律通过展开、变奏、交织在整个二十世纪物理学中扮演着类似音乐里的主题旋律的角色。1954年,为了解决人们无法确定大量发现的奇异粒子间相互作用的问题,杨振宁和米尔斯(R. Mills)给出一个确定高能粒子间相互作用的原理。他们注意到,通过魏尔的规范理论,电荷守恒和规范对称联系在一起。他们把规范对称推广到一般的“非阿贝尔”情形并和同位旋守恒联系起来,这同时又符合定域场的概念。1974年,相位因子被推广到不可积非阿贝尔相因子,从而把对称性和相位因子这两个主旋律紧密交织起来。“对称性支配相互作用”成了一个原理,并呼应爱因斯坦导出引力作用的方法。对非阿贝尔规范理论(即杨-米尔斯理论)的进一步研究导致了粒子物理的标准模型,但标准模型还有大问题。杨先生还提到,三个主旋律以及非阿贝尔规范理论在费曼的路径积分形式(path integral formalism)中漂亮地展现。
杨先生的报告中还有些很有趣的内容在书面版本(参考文献[1])中省略了。在讲完第一个主旋律时,杨先生对几位物理大师的风格言简意赅地评价如下。泡利(W. Pauli):功力(Power); 费米(E. Fermi):稳健、实力(Solidity, Strength); 海森堡(W. Heisenberg):深刻的洞察力(Deep insight); 狄拉克:笛卡尔式的纯粹(Cartesian purity)。讲完“对称性支配相互作用”和路径积分以后,杨先生还讲到规范场和当代数学中的纤维丛(fibre bundle)的紧密关系,并提及他与数学大师陈省身的交往。
我们知道,“对称性支配相互作用”是杨先生提出的革命性的思想。著名物理学家戴森(F. Dyson)认为杨先生是“保守的革命者”(“a conservative revolutionary”)。不可积非阿贝尔相因子以及规范场的数学意义也是杨先生和合作者(吴大峻教授)的贡献。杨先生的这个以及其它一些工作对纯数学也产生了并产生着极深刻和极深远的影响。杨先生在揭示物理与几何拓扑的深刻联系上起了关键作用。这个研究方向至今还是高能物理、凝聚态物理等多个领域的前沿。
最后,杨先生还从一个特别的高度探讨了三个主旋律在人类思想发展中最初的起源:量子化的思想与人类对测量单位的认识,以及德谟克利特(Democritus)的“原子”思想以及芝诺(Zeno)和庄周的连续性思想有关;对称性的概念来自对几何形态的美的认识,源于阿纳克西曼德(Anaximander)和毕达哥拉斯(Pythagoras)的思想;相位的概念则与月亮的圆缺的循环有关。杨先生指出,经过一个多世纪的数学家和物理学家努力,这三个原初的、不准确的概念发展成为二十世纪理论物理的主题旋律,并将继续引领物理学在下个三十至五十年的发展。
杨先生在他的报告中高瞻远瞩,抓住了二十世纪物理学的最主要的思想:三个主旋律及其发展、变奏和交织。全场听众屏息凝神,陶醉在这位关键性的参与者对这个伟大事业的充满感情的描述。杨先生的三个主旋律的说法真是再贴切不过了。从杨先生的演讲中,我们可以生动感受到物理学是怎么被充满个性的大师们创作出来的,联想到作曲家谱写交响乐。事实上,对于科学研究中的风格和品位,杨先生曾有过很多阐述(见参考文献[2]和[3])。杨先生自己就是物理学史上一位伟大的风格大师。杨先生与三个主旋律的谱写者交往密切,而那些大师又离十九世纪的经典物理学家很近。我真切地感到,物理学的伟大发展及其带来的人类文明的巨大进步是在多么短的时间里完成的!真是很精彩!
杨先生报告后,全场热烈的掌声经久不息。我想,这不仅是因为杨先生的这个报告的成功,更是因为杨先生在物理学上的伟大成功,以及深刻的历史洞察力和科学美鉴赏力。
而杨先生对二十世纪物理学主旋律的总结,不仅是在这个报告中,更是体现在物理学的实际发展中。杨先生集三个主旋律之大成。杨-米尔斯理论综合汇集三个主旋律,是这三个主旋律的共同高潮,同时也成为主导后来的物理发展的另一个主旋律。将来粒子物理的标准模型也许会被替代,但物理学家们相信,杨-米尔斯理论会长期重要下去。顺便提一下,杨先生在芝加哥大学做博士生时期就开始酝酿杨-米尔斯理论的思想(承蒙杨先生厚爱,笔者曾有幸仔细研读过有关笔记)。
会场上掌声平息后,作为统计物理学家的费希尔问杨先生, 二十一世纪物理学是不是主要将在复杂性上发展。这是统计物理和凝聚态物理的方向,所以是费希尔和安德森关心的问题。杨先生既是高能物理大师又是统计物理大师,学术境界特别崇高,眼光独特开阔,不存在高能物理学家与统计和凝聚态物理学家之间争论哪个更重要的问题。对于费希尔的不舍追问,杨先生给了一个不完全赞同,但以某种形式有所肯定的回答。安德森当时高兴地举起抱拳的双手。我注意到,安德森似乎常常认为并不满于其他一些高能物理学家有一种傲慢,却曾经在一次关于科学美的演讲中,特别提到规范场论,并且特别推崇杨先生在“杨振宁论文选集”(即参考文献[2])中的评述。
以上是对杨先生的巴黎报告的记述。当时我受聘于英国剑桥大学,是大会的普通参加者。在剑桥的几年中,我在大多数的日子里都要走过陈列在卡文迪许(Cavendish)实验室里的首任主任麦克斯韦(J.C. Maxwell,1831-1879)的实验仪器和办公桌,这时我会经常想起不朽的麦克斯韦方程,以及同样不朽的杨-米尔斯方程,因为后者是前者的非阿贝尔推广,或者说前者是后者的阿贝尔特例。2003至2004学年,我在美国伊利诺伊大学。2003年12月23日,杨先生在一个电子邮件中说他24日要回清华定居,并将他写的一首诗传真给我。这首诗就是“归根”诗。我非常荣幸收到的是一个打印于2003年12月3日、并注明“二OO三年十一月定稿”的竖行打印稿。单从打印的工整就可以看出作者的认真、朴实和即将归根的心情。作为一名喜爱物理学史的中国青年物理学工作者,我觉得杨先生从美国搬到中国与当年爱因斯坦从欧洲搬到美国这两件事在某些方面可以相比,而我收到和研读这首含义极其丰富的诗的心情是很激动的。“归根”诗曰:“昔负千寻质,高临九仞峰。深究对称意,胆识云霄冲。神州新天换,故园使命重。学子凌云志,我当指路松。千古三旋律,循循谈笑中。耄耋新事业,东篱归根翁。” 诗后注释道:“二OO二年我在巴黎的一个演讲题目是:‘二十世纪理论物理的三个主题旋律:量子化,对称与相位因子’”。
致谢:非常感谢杨振宁教授的珍贵指教以及对行文的有益评论。
参考文献:
[1] C. N. Yang, “Thematic melodies of Twentieth century theoretical physics: quantization, symmetry and phase factor”, International Journal of Modern Physics A,Vol.18,No.19 (2003) 3263-3272.
[2] C.N.Yang,“Selected Papers,1945-1980,with Commentary”(W.H.Freeman and Company,1983).
[3] “杨振宁文集”上下册 (华东师范大学出版社,1998).
保守的革命者——在杨振宁荣休晚宴上的讲话词
戴森(Dyson)(普林斯顿高等学术研究所)
我很高兴有这个机会来称颂我的老朋友和老同事富兰克·杨。我的题目是‘保守 的革命者’。这题目的涵义将在讲词末彰显。
1983 年富兰克为庆祝他的六十岁生日出版了‘文选(1945-1980)附评 注’。这是我最喜爱的书之一。书中的评注是他自己写的,用来解述各篇文章写作 时的情景。书里只收了他的文章的三分之一,是他自己选择的。这样做比由一个专 家委员会来挑选更能揭示他自己的思路和性格。所选的文章中有些是重要的,有些 是不重要的。有些是专业的,有些是通俗的。可是每一篇都是瑰宝。他不是试图在 五百页中塞进尽量多的、艰深的科学。他是试图在五百页中揭示一位伟大科学家的 精神,而做得十分成功。他选的这些文章既揭示了他个人的奋斗,也揭示了他的科 学成就。它们揭示了他的成就的深远的源泉,揭示了他对培育他的中国文化的骄 傲,也揭示了他对在中国和在美国的老师们的崇敬。它们还揭示了他对数学形式美 的热爱和同时掌握缤纷的实验物理世界和抽象的群论与纤维丛世界的能力。他巧妙 地将八十页的评注结集一起放在书的开始部分,而不是将它们附在各篇文章的后 面。这样,评注可以连续地读,成了他的科学自传,一部极好的自传。它以清楚而 简练的词句描述了他的一生。它朴实地描述了他的工作背后的强烈的感情和始终不 渝的忠诚。换言之,它描述了杨振宁之所以成为杨振宁。
书中最短的又最精彩的瑰宝之一是一篇两页长的,对费米的描述。它是作为费 米和他合写的一篇文章的序言,曾收录在费米的选集中。从 1946 年到 1949 年, 富兰克师从费米。他从费米那里学到的物理比从任何其他人那里学到的为多。费米 思考的方法在富兰克的思想中留下了无法磨灭的影响。他写道:‘我们懂得了,学 物理不应该只狭窄地学一个专业。学物理应该从平地开始,一块砖一块砖地砌,一 层一层地加高。我们懂得了,抽象化应在具体的基础工作之后,而绝非在它之 前。’
费米崇高实际的精神可以从 1954 年发表的杨-米尔斯这篇卓越的文章题目中 看到。今天任何一位谈到这篇文章的人,都会将它称为是引入非阿贝尔规范场的文 章。可是它的题目并没有提到非阿贝尔规范场。文章的题目是‘同位旋守恒与同位 旋规范不变性’。如何了解同位旋守恒这个物理问题出现在先,而抽象数学观念非 阿贝尔规范场出现在后。这是费米处理这类问题会用的方式,也是富兰克处理这个 问题所用的方式。费米的伟大在于他既懂得如何计算,又懂得如何倾听自然的声 音。在其一生中,富兰克均衡的处理了他的抽象数学的天才和费米对于物理细节的 脚踏实地的关注。
请允许我在这里简短的讲一个和这个讲话的主题无关的,有关费米的故事,它 和富兰克毫无关系。我不是费米的学生,但我有幸在我学术生涯中关键的时刻和费 米谈了二十分钟。我从费米这二十分钟中学到的比我从奥本海默(Oppenheimer) 二十年中学到的还多。1952 年我以为我有了一个强相互作用的好理论,组织了一 大批康奈尔大学的学生和博士后,按照这个理论来计算介子-质子之散射。我们运 算的结果和费米在芝加哥回旋加速器上量到的截面符合得很好。于是我得意的从依 色卡去芝加哥给费米看我们的结果。费米很客气和友好,但我们的结果并没有引起 他的兴趣。他说:‘计算的途径有两种。第一种,是我所愿意采用的,是先有一幅 清晰的物理图象。第二种是严格的数学架构。你的则两种都不是。’这既结束了他 和我的对话,也终结了我们的理论。以后我们弄清楚了,由于没有将矢量相互作用 考虑在内,我们的理论不可能是正确的,而费米直觉地看出了这个理论必然是错误 的。在这二十分钟里,他的脚踏实地的见识省掉了我们的无谓的计算。这个教训富 兰克是无需要学习的,因为当他在芝加哥做学生时,已经充分吸取了费米的见识。
在选集发表后的十五年中,富兰克没有闲着。1995 年另一本书出版了,不是 他自己而是他的朋友们写的,是庆祝他七十岁生日的文集。书的题目是‘杨振宁 ──二十世纪一位伟大的物理学家’。隐藏在书中的专业文章里,有一些个人的颂 赞和回忆。它们描述了富兰克如何积极帮助科学在三个中国社会──中华人民共和 国、台湾和香港的成长和繁荣。富兰克很高兴能够偿还他所欠他的故土和文化的 债。
这两本书中都没有收入的是富兰克两年前写的题为‘父亲和我’一文。这是献 给他的父亲,一位 1973 年去世的数学教授的文章。它极精彩而微妙地描述了他和 父亲的关系,以及分离给二人带来的痛苦。他的父亲在艰难的岁月里留在中国,而 就在这段时间中富兰克在美国成长为名家。他们都知道还是这样好:没有美国,富 兰克不会成为一位世界级的科学家;不住在祖国,他的父亲将成为无根之木。然而 分离也深深地伤害了两人。对富兰克来说,他个人和父亲的分离,同美国和中国在 政治上的隔绝是一场悲剧的两面。很幸运,尼克松总统适时地决定承认中华人民共 和国。因此,富兰克能够在他父亲去世以前访问中国,能够在他父亲病危时坐在他 的床边。在选集的评注中,富兰克描述了他在 1964 年如何困难地作出成为美国公 民的决定。这决定正式承认了他脱离中国,脱离他的父亲。他写道:‘我父亲…… 1928 年在芝加哥大学获得博士学位。他游历甚广。但我知道,直到临终前,对于 我的放弃故国,他在心底里的一角始终没有宽恕过我。’
‘父亲和我’有一个快乐的结尾,一个光辉的重圆。富兰克描述 1997 年 7 月 1 日清晨零时,他站在香港会议展览中心,凝视着英国国旗缓缓下降,中国国 旗缓缓上升,乐队奏着‘起来,不愿做奴隶的人们’,他写道:‘父亲如果能目睹 这历史性的,象征中华民族复兴的仪式,一定比我还要激动。……他们那一辈的中 国知识分子,目睹洋人在租界中的专横,……说不完的外人欺凌……他们是多么盼 望有一天能看到站起来了的富强的中国,能看到大英帝国落旗退兵,能看到中国国 旗骄傲地向全世界宣称:这是中国的土地。这一天,1997 年 7 月 1 日,正是他 们一生梦寐以求的一天。’
富兰克那夜站在那里,他的,和他父亲的,对重圆的深层感触是使我们动心 的。而对我,他所表达的骄傲和满足的心情,特别引起了共鸣。我也属于一个伟大 而古老的文明。我在英国的故乡也是 Alfred 这位学者国王的故乡。一千一百年 前,当唐朝在中国建立了在中国持续千年之久的科举制度时,Alfred 将我的故乡 变为一个卓越的学问中心。我们的 Alfred 国王将拉丁文典籍译成英文,和唐朝诗 人差不多同时代。富兰克在他的选集前面引用了杜甫的诗句:‘文章千古事,得失 寸心知’。
和富兰克一样,我也离开了故土,成为美国公民。我仍记得我在 Trenton 受 到的屈辱。那一天我宣誓忠于美国,主持仪式的无知先生祝贺我逃离了奴隶之乡来 到了自由之邦。我好不容易才忍住了没有大叫,我的祖辈们解放我们的奴隶比他们 的祖辈们解放他们的奴隶要早得多。我和富兰克对美国有同样的矛盾的感情。这个 国家对我们两人都如此的慷慨,可是对我们的古老的文明又如此不了解。我也感受 了他在香港亲睹和平地降下英国国旗,升起中国国旗时的骄傲。在那一瞬间我们这 两国古老的文明短暂地走在一道,催生了一个崭新的事物。
五年前我很荣幸在费城美国哲学学会授予他富兰克林奖章的仪式上讲话。我们 聚集在学会的有历史意义的会议室中。学会创始人富兰克林和学会最活跃的成员之 一杰弗逊的画像俯视着我们。我们知道他将他的大儿子取名为富兰克林,因为他对 富兰克林特别崇敬。我愿用我在那个愉快场合称颂富兰克的话来结束今天的讲话。
杨教授是继爱因斯坦和狄拉克之后,二十世纪物理学的卓越的设计师。从当年 在中国当学生到以后成为石溪的哲人,引导他的思考的一直是他对精确分析和数学 形式美的热爱。这种热爱导致了他对物理学最深远的和最有创见的贡献──和米尔 斯发现的非阿贝尔规范场。随着时间的推移,他所发现的非阿贝尔规范场已渐渐成 为比宇称不守恒更美妙更重要的贡献。后者使他得到了诺贝尔奖。发现宇称不守 恒,发现左手和右手手套并不在各方面都对称,是一项了不起的破坏行动,它摧毁 了在前进道路上的思维障碍。与之相反,非阿贝尔规范场奠定了新的思维结构的基 石,这个结构以后经过三十年才建立起来。今天当代理论描述的,并为当代实验证 实了的物质的本质,是各种非阿贝尔规范场的组合。他们为杨在四十五年前首先猜 测到的数学对称性所支配。
和重建城市以及国际政治一样,在科学中摧毁一个老的结构比建立一个持久的 新结构容易。革命领袖可以分为两类:像罗伯斯庇尔和列宁,他们摧毁的比创建的 为多;像富兰克林和华盛顿,他们建立的比摧毁的为多。无疑,杨是属于后一类的 革命者。他是一位保守的革命者。和富兰克林和华盛顿一样,他爱护过去,尽可能 少摧毁它。他对西方科学的杰出思维传统和对中国祖先的杰出文化传统同样崇敬。
杨喜欢引用爱因斯坦的话:‘创造的源泉在于数学,因此,从某个意义上讲, 我认为,纯思维可以掌握现实,像古人所梦想的那样。’在另一场合,杨讲道: ‘乍听起来,一个人的爱憎和风格竟与他对物理学的贡献有如此密切关系,也许会 令人感到奇怪,因为物理学一般人认为是一门客观地研究物质世界的学问。然而, 物质世界具有结构,而一个人对这些结构的洞察力,对这些结构的某些特点的喜 爱,某些特点的憎厌,正是他形成自己风格的要素。因此,爱憎和风格之于科学研 究,就像他们对文学、艺术和音乐一样至关重要,这其实并不是稀奇的事情。’杨 对数学美的感受,照亮了他所有的工作。它使得他的相对最不重要的计算成为袖珍 的艺术品,使得他的深入的猜测成为杰作。它使他,正如使爱因斯坦和狄拉克一 样,对自然的神秘能够比别人看得更远一点。 ───────────────
* 这是在杨振宁荣休晚宴上的讲话词,一九九九年五月廿二日于纽约州石溪
杨振宁的生平和时代
一位诺贝尔奖得奖人回顾在物理学和数学十字路口度过的一生
Earl Lane作,范世藩、杨振玉 译人们赞扬在理论物理前沿度过了半个世纪的诺贝尔奖得奖人杨振 宁是一位坚韧不拔、具数学天才的科学家。他致力于揭示自然的对称 性,而这些对称性常常是隐藏在杂乱的实验物理结果的后面。
七十七岁的杨振宁刚刚退休,他在晚年依然令人敬畏,不怕向当 代流行的思潮挑战,清醒地意识到面对复杂的宇宙,人们的才智的局 限性。他的许多同事都在谈论找到一个“解释一切的理论”的可能性。 即一个描述宇宙中所有的作用力和基本粒子的统一的理论。杨振宁曾 为物理学家提供了从事这种探索所需的一些重要的数学工具,可是他 却对这种可能性深感怀疑。
“我想‘解释一切的理论’是一个不好的命题。我不相信有人能 触及解释一切的理论。自然是非常奇妙的,它的深奥无人能探测。我 们就算有上千亿个神经细胞,又怎么能和自然的无限深奥相比呢?” 新近在纽约州立大学石溪校区杨振宁的办公室的一次采访中他这样说。 他继续说:“听起来我好像是笃信宗教的。我不信宗教。可是当你触 及这样基本的问题时,确是很接近宗教。这不是形式的宗教。可是在 发现宇宙的某些基本结构时的惊叹和畏惧甚至比形式的宗教还更宗教 一些。”
杨振宁长时期在看来是神秘的物理学和数学的十字路口工作。在 这个领域内,一组漂亮的方程式可以是灵感的源泉,甚至可以在还没 有实验证据以前就洞察物理世界是怎样运转的。这是一个外行很难懂 的世界,其中有充满了希腊字母的方程式的黑板,有寻求用数学去解 决问题的“品味”和“风格”,有寻求用正确语言来描述物理世界的 出自内心的灵感。
物理学家戴森(Dyson)去年在石溪为杨振宁退休所举行的学术讨 论会上说:“杨振宁对数学的美妙的品味照耀着他所有的工作。它使 他的不是那么重要的工作成为精致的艺术品,使他的深奥的推测成为 杰作。”这使得他“对于自然神秘的结构比别人看得更深远一些”。
杨振宁已有华发,可是看起来比他的实际年龄年轻得多。他仍穿 梭于纽约和远东之间。他和香港以及北京的大学有密切的联系,并且 是设在南朝鲜汉城的一个理论物理中心的主席。
在关于他的生活和时代的一次广泛的谈话中,杨振宁谈到他的物 理学生涯,谈到他没有能从事某些领域的研究而感到的遗憾。他推测 下几十年占主导地位的将是生物学和应用物理学而不是对物质基本结 构的研究。
杨振宁也谈到他在中国童年和他长时间为沟通美国和自己的祖国 在科学和文化方面的差异所作的努力。杨振宁谈到他担心中美关系的 裂痕会扩大,以及由于新近对台湾出生的物理学家李文和间谍活动嫌 疑的调查,将为亚洲和亚裔美国科学家带来的困难。杨振宁说:“我 很担心,如果中美关系继续沿着过去五、六年的趋势发展下去,将会 是一场灾难。”1971年中美关系开始解冻,杨振宁自1945年到美国来 当研究生以后第一次回到中国大陆。他会见了已故的周恩来和中国的 其他领导人,帮助开展了两国之间的科学合作。他担心这些合作将面 临危险。
那时候,当他从国外旅行回来后,联邦调查局和中央情报局的人 员常常去找他。中央情报局的官员第一次去找杨振宁时杨要让他的秘 书记录他们的谈话,以免误解。杨振宁继续保持和中国的密切联系, 他说:“联邦调查局和中央情报局近来没有再来找我的麻烦。”
杨振宁最关心的是科学而不是政治。他谈到自己的一些经历:一 个从中国偏僻地区一个落后的城市来的年轻学生,怎么会有幸参与二 十世纪一个最主要的思想革命。这场革命是试图用一个统一的方法来 了解自然的无穷多样性,从混沌的星球爆炸到电子环绕原子核的颤动。
如杨振宁所说的,这是一个由像爱因斯坦那样的巨人建立起来的 辉煌事业。爱因斯坦曾是瑞士专利局的一位办事员,他在1905年写出 了《狭义相对论》。它阐明物质和能量是等价的和没有东西的运动速 度可以超过光速。十年以后,爱因斯坦在他的《广义相对论》用几何 学将重力描述为包在客体的空间—时间域中的外衣。其他巨人如狄拉 克(Dirac)、薛定谔(Schrōdinger)和海森伯(Heiscnberg)在二 十年代根据实验结果提出了量子力学。它用称为量子的、分立的能量 束来描述原子王国,并提出了测不准原理,即对一个粒子的位置量度 得愈精确,那么对它的速度的量度就愈不精确(反之亦然)。量子理 论将基本粒子看作是兼具波动性和粒子性的。虽然爱因斯坦一生都被 量子理论中的测不准原理所困扰,可是经过这么些年,已经证明量子 理论有非常强的活力。
在这个背景下,一些科学家认为杨振宁是二十世纪后半叶最有影 响的理论物理学家之一。像爱因斯坦一样,他孜孜不倦地探索如何用 几何学来描述物理世界。他也很注意抽象的对称概念,它们可以揭示 自然界中的新现象。
1956年杨振宁第一次出名。那一年他和李政道共同发表了一篇文 章,推翻了物理学的中心信息之一——宇称守恒(基本粒子和它们的 镜象的表现是完全相同的)。因为这个工作,两人获得了1957年的诺 贝尔奖。
从长远来看,1954年杨振宁和已故的米尔斯(Mills)的开拓性的 工作却更为重要。那一年,两人都在布洛克海文国立实验室工作。他 们提出了一个称为非阿贝尔规范场的理论结构。以后证明它是以统一 的方式描述作用力和基本粒子的关键。布洛克海文的一位理论物理学 家马奇努(Marciano)说:“当它在1954年写成时,争论极大。一些 人认为它和物理世界无关。”当时,杨和米尔斯没有继续发展下去。 可是以后证明,这个以微分几何和纤维丛这样的抽象世界中抽提出来 的数学,正是为描述像磁、电、强核力,也许还有重大相互作用中, 中界作用力的粒子交换所。戴森讲道:“我要说,在杨振宁的工作中 最最重要的是规范场。已经证明这比他和李政道关于宇称的工作要重 要得多。”
杨振宁和李政道的关系变得愈来愈紧张,两人在1962年分手。杨 振宁拒绝谈论是什么原因使得他们的关系变得紧张的。他说:“这是 我生命中令我非常失望的一件事情。我要说,这是一个悲剧。”他们 两人已经有几十年没有讲话了。
他们两位的同事说道,无法猜测如果他们两人继续合作下去,会 有多大的成就。杨振宁本人推测,他们可能参与弱相互作用力的研究, 这是一个描述放射性衰变和电磁作用力的统一的数学架构。温伯格 (Weinberg)、萨拉姆(Salam)和格拉萧(Glashow)在1979年就因 为“电弱”理论得了诺贝尔奖。
杨振宁扎根于数学,但是他指出,自己一生的工作不是脱离现实 世界的形而上学的游戏。四十年代后期他刚去芝加哥大学研究院时曾 打算成为实验物理学家。可是他很快就了解自己的动手能力很差。实 验室的同事们开玩笑道:“哪里出爆,那里就有杨振宁。”
杨振宁对于他早年从事过的实验物理一直没有忘怀。不过当他转 向理论物理后,他所需要的工具只是铅笔和笔记本。曾任布洛克海文 国立实验室主任的实验物理学家萨奥斯(Samios)说:“杨振宁是一 位极具数学头脑的人,然而由于早年的学历,他对实验细节非常有兴 趣。他喜欢和实验学家们交谈,对于优美的实验极为欣赏。”
对于像杨振宁这样的理论物理学家,在揭示自然界的结构时,数 学和实验室中进行的实验同样重要。杨振宁说:“爱因斯坦《广义相 对论》是一个非常优美和深奥的创作”,它不是根据实验结果得出来 的。爱因斯坦直觉地想到,物体在宇宙中受到重力的拽拉,可以看作 是周围时—空结构的弯曲。他用已有的黎曼几何来描述他的新理论。 后来,星球发出的光线接近太阳时因重力而弯曲的实验,证明爱因斯 坦是对的。
对于物理学家最大的挑战,依然是提出一个统一的理论,它既适 用于以重力为主的极大王国,又适用于由量子所主宰的极小王国。物 理学家在七十年代已经在这方面获得进展。他们提出一个称为标准模 型的理论。这个理论有两条腿:温伯格、萨拉姆和格拉萧的“电弱” 理论和“量子色动力学”。后者描述把粒子的基本构件——夸克束缚 的质子和中子内的各种作用力。这两条腿都是由杨和米尔斯所构筑的 数学架引伸出来的。可是标准模型并没有将重力考虑在内。
目前,弦线理论可能可以克服这个缺点。这个理论假定存在微小 的一维弦线,它的不同的振动方式可以解释所有的基本粒子和包括重 力在内的作用力。这个理论经过修改后要求十或十一维时—空,而不 是我们熟悉的四维时空,即时间这一维加上立体几何的三维。弦线理 论提出来已经二十多年,它在年轻的理论物理学家中很流行。可是杨 振宁在晚年时是不同意这个理论的。正像爱因斯坦对量子力学的一些 内容有不同的意见,杨振宁怀疑弦线理论或其派生的理论是否能将所 有客观存在的现实都放进一个简洁的包装中。
爱因斯坦的理论和量子力学在提出后几年内就都得到了实验证明。 杨振宁说:“弦线理论并没有得到实验证明。它太不定形,太模糊。” 问题部分地在于,为探索弦线的影响,需要极高的能量,更强的粒子 加速器。如何写出一个可以工作的理论,并从事十维计算也是一个问 题。正如温伯格新近写的:“我们怎么会有这样的想法呢?我们需要 提出一个真正是基本的理论,这个理论是用来描述一个世界,在这个 世界中人们对于空间—时间的直觉都不适用了。”对于弦线理论是否 正确,温伯格和另外一些人也许没有杨振宁那么悲观。可是没有人低 估它的困难。
杨振宁提出物理学正经历一个过渡期。不断地寻找更快更小的计 算机晶片等的应用研究,将会比基础研究对年轻人更有吸引力。他说: “很清楚,在未来的三十到五十年中,人们将更注意物理学的应用。 其理由并不是因为所有的基本问题都已经解决了,而是因为更深入地 探索物质的基本结构变得愈来愈贵。”他又说,1993年国会决定中止 建造超导超级对撞机是一个信号,高能物理有充裕的经费的时代已经 结束了。超导超级对撞机是要在美国德克萨斯州建造的一个基本粒子 加速器,它的直径将达54哩。
杨振宁预言,计算机工业的实际需求将会推动界于微观和宏观之 间的物理学的发展,在比高能物理的亚原子前沿为粗的水平,对物质 进行研究。他承认许多分析家们早已预言,二十一世纪将是生物学的 世纪,就像刚刚过去的二十世纪被称为物理学的世纪一样。
是什么环境使杨振宁能在占支配地位和物理学中起重要作用呢? 听他自己说,在他的成功中,运气和抱负同样重要。
杨振宁早年处于一个更像是中世纪的而不是现代的社会。他得益 于幸运的家庭环境以及和同事与学者们的联系。这些为他进入更广阔 的知识和文化世界的旅程铺平了道路。反过来,他正通过不断努力在 亚洲建立一流的研究中心为回报。
杨振宁生长在中国中部一个围有城墙的城市——合肥。当时,这 个城市的街道是没有路面的,城门很窄,以致三十年代第一部汽车开 来时无法通过。大部分居民是文盲。由于闭塞,杨振宁直到六岁才第 一次看见香蕉。
杨振宁的父亲是当地中学的数学教师。他通过了一次奖学金考试, 得以出国,去芝加哥大学读书,回国后在厦门大学教书,以后去了北 京清华大学。
杨振宁本人追随他父亲走上了学术道路。他说:“我很幸运,上 百万和我同年龄的人不是饿死就是面对军阀混战。”他住在北京一个 学术性的社区内,沉浸在一个重视研究、重视知识的社区中。他的父 亲很快就发现儿子有数学天才,可是并没有直接教他数学。杨振宁说: “父亲的哲学是‘不要着急’。”在谈天时他偶尔会向儿子提出数学 难题。可是父亲也认识到教育需要均衡。在杨振宁念完中学初一时, 父亲请了一位同事来教他中国古文。经过两个夏天的紧张学习,年轻 的杨振宁能背诵孔子的门徒孟子的全部著作。
1937年日本入侵,杨振宁的父亲被迫离开北京,在昆明西南联合 大学任教。杨振宁继续走好运。年轻的杨振宁不久进了这所大学,受 教于一些当时中国最杰出的科学家。他们之中有些以后去了美国,其 中包括陈省身。陈省身现在已经从伯克莱加州大学退休,许多人都认 为他是现在活着的最重要的微分几何学家。
在昆明时,杨振宁开始提高他的英文。他决定不用字典来念英文 小说。他选的第一本小说是斯蒂文森的《金银岛》。这部小说里有和 大海有关的俚语,因而很难念。他花了一个星期,念完了这本书,接 着念奥斯汀的《傲慢与偏见》。在熟读这两本书以后,杨振宁说: “以后就容易了。”
杨振宁还有去西方世界的另一原因:他对美国初期的科学家兼政 治家富兰克林很崇敬,富兰克林的自传激励了杨振宁。去美国后他取 名为富兰克,并将第一个孩子的英文名字取为富兰克林。
1945年杨振宁得到庚子赔款奖学金去了美国。美国因为1900年义 和团反对外国人的起义,从中国索取了一笔赔款,以后把这笔钱退还 给北京用于教育。普林斯顿大学接受了杨振宁,可是他要拜才华横溢 的意大利物理学家费米(Fermi)为师,因此去了芝加哥大学并在以后 被称为氢弹之父的泰勒(Teller)的指导下写了博士论文。论文写好 后只有四页。泰勒说服杨振宁,无论如何,一篇博士论文只有四页总 是太短了,要他加长。他照办了,加到了二十三页。
在物理学有了卓越的成就以后,他又转向远东。杨振宁将把他的 文稿与信件捐赠给香港中文大学而不是给石溪纽约州立大学。他是中 文大学的访问教授。杨振宁也没有排除他搬回中国的可能性,因为回 去后他和与他结缡已五十年的妻子杜致礼会得到更好的照顾。(新近, 致礼在石溪州立大学的医院动了三次肿瘤手术,结果良好。)
杨振宁在长岛还是感到很自在,也不像是要搬到远离他的三位已 经成年的孩子身边。他们三位都已得到科学方面的学位。杨振宁说: “他们是美国人。他们接触的中国文化很少。”长子光诺毕业于密西 根大学计算机科学系,现在是纽约州西彻斯特县的一位财务顾问。次 子光宇是一位化学博士,住在纽约城,为J.P.Marg财务公司分析化 学工业。女儿又礼是蒙太拿州列文斯登县的一位医生。杨振宁在 1964年成为美国公民。他说:“我们在美国过得很不错。在这里我们 有许多朋友。我们在两个社会中都很自在。”
在石溪为他的退休举行的学术讨论会结束时,杨振宁谈到他在六 十岁时的一个“伟大和意义深远的发现”:“生命是有限的”。他念 了九世纪的一位中国诗人李商隐的诗句:
夕阳无限好,
只是近黄昏。
二十世纪初,另一位作家,也是杨振宁父亲的朋友(译者注:朱 自清),把这两行诗句改为:
但得夕阳无限好,
何须惆怅近黄昏?
在历经一生对自然的神秘的思考以后,杨振宁认为这一改造更精 确地描述了他晚年的想法。
(原文载美国2000年2月1日《Newsday》)
光明日报2000年05月01日
Gauge theories--1. Foreword
by suprathinker
Responding to the kind invitation of the Shortriver Scholar, the XYS Chief Scientist and "Mentor in PhD and Postdoc Programmes", I will write a series on gauge theories, the much-touted and much-lauded physical theories of the 20th century and believed to remain the dominant theme in the physics of the 21st century.
Gauge symmetry is a great discovery that revolutinized our understanding of physics, particularly the fundamental interactions of the fields/particles underlying our nature. With this idea, we have an amazingly straightforward "standard model" that unifies electromagnetic, strong and weak forces and all elementary paricles can be packed into a single box perfectly.Some people even believe that the last interaction, i.e., gravity, can be treated in a similar way and all four fundamental interactions can be unified by superstring theory.
In the next few postings, I'll explain the essence of gauge symmetry and its success in particle physics and string theory so that you'll have a grip of the major ideas and achievements of the gauge theories. It will be utterly different from what you have read about the same topic because gauge symmetry will be scrutinized in a hitherto unapproached perspective. Of course, you know it has to be like that, otherwise, why don't I just give you a Wiki link or the webpage of a some physics professor?
After the introduction, I'll explain the problems in current physics theories of fundamental interactions and in passing, I'll expose to you the misbelieves and blind spots of the major players in the field. The major purpose of this series is to point out that gauge symmetry has come to its end. It belongs to the past. New paradigms are emerging and will bloom. To support such a rebellious and hated argument, you know I'll have to devote much to explaining why it is so.
I'm keenly aware that it is an exceptional honor to receive an assignment from Scholar Shortriver, our Chief Scientist at the XYS Insitute. I'll surely do my best to write it well. However,I am not sure how regular my postings will be, but let me try once a week first.
Gauge Theories 2. From Athens 300 BC to Geneva 2011 AD
2.1 Atoms-A Mystery of Two Millenia
Humankind’s serious quest to understand our nature dates back at least to ancient Greece when came out a unique group of people who not merely gazed at the stars in the vast sky or watched the people and things around them but also pondered the reason behind the mystery of those remote objects, conjectured the inner structure of various kinds of matter around them and tested new forms of state management. Along the way, they developed the logic system, axiomatic mathematics, astronomy, physics and democracy among other great achievements. Some of them such as logic, number theory and geometry are taught and practiced today almost in exactly the same way as over 2000 years ago. Ancient Greek civilization is a rare bout of intellectual explosion in the history human evolution. To me it is a huge mystery how they could reach such a highland of intelligence and rationality. We are exceptionally blessed to have such a golden time in our history and should feel eternally grateful for their contributions to the entire humankind. It is a great comfort to see their spirit perpetually planted in our minds and more and more people becoming the spiritual descendants of the ancient Greeks. Of their great achievements, relevant to this series is that they hypothesized the existence of atoms, the tiny, unbroken components of all matter. Different combinations of atoms create different forms and kinds of matter. It is a tremendous simplification of our nature. One can never overestimate the influences of this philosophy on the people who set out to search for the answer to a natural phenomenon. In fact, it has become the most important drive of modern science and technology.With that said, atomic theory of ancient Greece largely remained a pure speculation for more than 2000 years. Alchemists may protest this assessment, but their contributions are limited to the synthesis of some new compounds only. Fancy and useful these things may be, the significance to the understanding of the structure of matter is null. No substantial progress was made until the age of industrial revolution of 18th-19th century. The indisputable, quantitative evidence of the existence of atoms was provided by a colorblind British, John Dalton. The chemical reactions he performed may be called trivial even in his time, but his capacity of logic inference can only be called genius. In a few years, his theory was warmly accepted and applied by the mainstream of science. A few decades later, a Russian named Dmitri Mendeleev tabulated the elements that had been discovered. The table reveals a hidden, astonishing simplicity, i.e., all elements are somehow related to each other and form a hierarchical family. Elements sharing physical or chemical properties such as density, color, luster, conductivity, reactivity etc can be grouped into rows and columns, called periods and groups, respectively.
It would take the world another over 100 years to have a full understanding of the significance of the periodical table. Indeed, there are still many puzzles about the table today. Mendeleev’s periodical table was accepted almost immediately because new elements that were predicted by his table were found with exactly the same properties as predicted. Unlike the ancient Greek’s atoms, Dalton’s atoms have many kinds, each element having its own atoms. Like ancient Greek’s atoms, Dalton’s atoms are unbroken. This property, however, with the efforts of great scientists such as Svante Arrhenius, James Thompson, was found to be untrue. Atoms do have their own internal structure. The description and explanation of atomic structure are the major tasks of the physicist and chemists of the early 20th century. With a very simple apparatus called cathode ray tube, Thompson discovered electrons and measure its charge/mass ratio. He further built up an atomic model in which the negative and positive charges are more or less uniformly mixed together to form a tiny ‘jelly’. In less than 20 years, this model was overthrown by Ernest Rutherford who proved that there is a tiny but massive nucleus in the atom. His atomic model is like a tiny solar system in which the heavy ‘sun’ is positively charged and the light ‘planets’ are negatively charged. While the stability of our solar system is maintained by the gravitation attraction between the sun and the planets, the stability of the atom is maintained by the electric attraction between the ‘sun’ and the ‘planets’. This model is still used in high school and college textbooks today. Like the solar system where inner planets have lower energies and hard to leave the sun, the electrons closer to the nucleus have lower energies and harder to leave the atom. Unlike the solar system where each planet runs on its own orbit (we never observe a planet make a change of their orbit), the electrons in an atom may make a jump, or transition, i.e., they may change their orbits. When an electron gets extra energy from, e.g., light, that may move to an orbit of higher energy. On the other hand, an electron in the orbit of higher energy may jump ‘down’ to lower orbit by emitting light (photon). With this ‘dynamic planet’ model, the mysterious spectrum can be understood. The answer to questions such as “why does sodium, when burned, emit its characteristic yellow color while magnesium emits a different, bright white color?” becomes obviously clear.
Things looked perfectly simple and fine. People started to give a sigh of relief. The atoms are tiny solar systems and our solar system has many tiny kids or grandkids, isn’t it a beautiful picture? The sensitive reader may see a kind of gauge symmetry here. If we make a scale change, or gauge transformation, our solar system becomes an atom or vice versa. Physical theories work the same way in different scales (gauges). (caution: we know that theories with this kind of gauge symmetry is rare because energy scale and size scale are related to each, that is why we do not see tiny solar systems very often. You see gauge has to have something more than ‘scale’. ).
However, the tiny solar system model, or planets model, was found to be erroneous. As a well-known phenomenon, if a charge has acceleration, it will emit electromagnetic wave and loses energy. For example, the arctic lights are the consequence of charged particles accelerated by the earth’s magnetic field. An electron moving in a circular orbit certainly has acceleration. According to classical electromagnetism, then, an electron has to emit light and lose its energy and finally it would crash into the nucleus. That is to say, the planet model cannot explain why the atoms are stable. Electrons are there moving around the nucleus but they do not lose energy and swirl into the nucleus.
It took about 10 years to solve the problem. To get the answer, a new kind of physics, suitable (and maybe uniquely applicable) in the microscopic scale, was established. It is a rare kind of revolution in science, a revolution that puts giants like Newton, Maxwell and Einstein in an embarrassing situation. That is quantum mechanics. Initially, it was built to answer a very specific, important but not that earth-shaking, question of the stability of atoms, but its consequence is epoch. You may find quantum mechanics book thick and frightening, but it can be summarized into a single, short sentence: quantum mechanics says that the order of making two (hence more) measurements matters. You may get a different result if you change the order of two measurements. It sounds odd, you may say, how does it relate to the question of the stability of atoms? You may also protest, why is it such a big deal? We all know that the order of dating and making love are very important, does that make us a quantum mechanical object?
I think it’s a good time for both you and me to say “給我一個突破”. See you next week.
2.2. Reality and How to Describe It
Recapping the content of 2.1: Ancient Greeks guessed that all matter consists of tiny, identical, unbroken atoms; Dalton confirmed this idea with quantitative experiments and proposed that different elements have different atoms; Mendeleev discovered that all elements are related to each other; Thompson proved the existence of electrons; Rutherford established the existence of nucleus; A planet model of the atom was proposed that can explain the spectrum but cannot explain the stability of atoms—why a supposedly accelerating electron does not radiate energy and crashed into the nucleus. This puzzle led to the birth of quantum mechanics. We concluded 2.1 by mentioning that the order of making measurements is important, or roughly speaking, the order of doing things is important. Making love before dating and dating before making love may have different consequences as we all know. That’s what quantum mechanics all about, if you think hard enough. Therefore, quantum mechanics is not that outlandish. People talking about it but not understanding it make it sound so. Now let me show you why quantum mechanics is simple and it should be the way our nature operates.To start, we mention that the new physics in microscopic world was constructed in the 1920s by a group of young people, many of them being German-speaking boys. Old players had become either too exhausted to follow the new ideas or too conservative to make a shift of way of thinking. Max Planck who first proposed the concept of quantum thought that his idea would be swept into the dustbin of history and decided to accept the dismaying reality that his then 20-something quantum theory would be abandoned soon. He neither made any defensive moves nor tried to find a fix. Some people suggested that Planck had lost interest in physics after 1910s because of a series of family tragedies (in 10 years from 1909 to 1919, his wife and three of four children died). Lorentz was too old to attend conferences. Although Niels Bohr has been revered by physicists for his role in the quantum revolutions, his specific contributions to this new physics are either insignificant or defective. Albert Einstein could not catch up with the tide and turned himself into a foul crier. That is the golden time of physics for the young academic proletariats and the nightmare for the establishment. New discoveries come out like avalanches, old men scream in fear and hatred but shrink away swiftly, while young boys engage head-on fights and win one battle after another. To have a feel of how great these kids were, we only need a very short list: in 1924, Louis de Broglie (32) proposed the wave-particle duality; in 1924, Wolfgang Pauli (24) proposed the existence of electron spin and exclusion principle; in 1925, Weiner Heisenberg (24), Pascual Jordan (23) and Max Born (43) proposed the correct mathematical framework of quantum mechanics called matrix mechanics; in 1926, Erwin Schrodinger (39) completed another version of quantum mechanics and solved the spectrum of hydrogen atom; in 1927, Heisenberg (26) published his famous principle of uncertainty; in 1928, Paul Dirac (26) proposed the quantum mechanics that is compatible with relativity theory, i.e., applicable to the cases where speed addition violates the ordinary rule. Dirac’s theory also solved the problem of the origin of electron spin as a consequence of relativity and led to the birth of quantum field theories. In 1930, Dirac (28) published his famous book The Principles of Quantum Mechanics, which laid the solid and concise foundation of quantum mechanics, i.e., quantum mechanics is best expressed with the functional analysis in the Hilbert space, which not only cleaned up the controversies involving Schrodinger’s wave mechanics and Heisenberg’s matrix mechanics, but also provided a consistent and straightforward tool for calculating all kinds of phenomena. In less than 10 years, the pursuit of the answer to a seemingly trivial question of why the revolving electrons in an atom do not radiate energy and crash into the nucleus brought an unprecedented revolution in physics. Let us continue the story of the last posting and explain the essence of quantum mechanics.
Ffirst allow me to murmur a little more about the order of making measurements and along the way I will explain a mysterious trick called “quantization” that has become a standard procedure in all modern physical theories, including quantum gauge theories. In classical physics, we have no trouble with the order of multiplication, e.g., nobody would doubt the legitimacy of p*x = x*p. The whole story of quantum mechanics and its ramifications, or the splendid downfall of classical physics edifice, can be condensed into a short equation: AB may not be equal to BA for two physical quantities. Of course, this is just another way of saying ‘making love before dating is different from dating before making love’. If you have trouble with this equivalence, you need to stop here and think about it for a while. When we have a result on some physical quantity, such as the position or speed or energy, we must have made a measurement on it. An unspoken premise of modern science is that only what you measure counts. One should not utter a single word on something if one has not measured it beforehand. This is the very reason why science is science, not voodoo tricks. You may say, what a big deal is it, “you say nothing about making love with that hot girl if you have not been laid yet”, isn’t it obvious? Yeah, it IS obvious. It IS dumbly obvious. However, it is the mostly unobserved rule of reasoning for the people talking about science, particularly physics. For instance, one may regard the following statement obviously and perfectly valid: “Even if I do not look at the moon, I still can assume the moon is there.” Badly wrong! Logically wrong! When you say the moon is out there, this means you have a measurement result on the moon that shows that the moon is there. Logically, one cannot make such a claim when one has not made a measurement on the moon. If you carefully examine why you believe the moon is still there even if you do not look at it is because you justify your claim based on experience rather than on logic or observation. Empirically, you assume that the moon never disappears. It is always there. However, how true is it? Imagine that we have billions of solar systems. Most of them are just the same as ours, but some of them may be in the stage of being destroyed. Now we have billions of people being asked of such a question: “Is your moon still there even if you do not see it?”, then you can safely say some of them would find their answer being proven wrong immediately—some moons are gone in their solar system because their solar systems are being destroyed. So now you should see that the statement “even if I do not look at the moon, I still can assume the moon is there” is equally absurd as “1+1 may be 3.2.” or “that girl is a great sex partner although I never slept with her.” A terser and more polite way of saying it is: “Shut up if you haven’t done the damn thing!” That is the embodiment of the true spirit of science. Do not be so confident to presume that your gal is not sleeping with other guy when she is not with you!
To extend this logic a little bit further: Reality is a collection of information that you have acquired. Nothing a priori, nothing hypothetical, nothing imagined, may come into the description on reality. This may look not surprising at all and even cliché, but people can easily go awry and cannot adhere to it consistently when confronting a specific practical problem.
What is an electron? Now you know the correct answer: an electron is a physical entity described by a number of observables. More specifically, an electron = mass + charge + spin. That’s all we know about an electron. That’s all we can assume about an electron when we talk about it. Forget about the shape, size, color, spirit. We have none of them.
Back to our dear but pranky atoms. There are electrons and nucleus in an atom. This is a fact because people performed countless experiments to validate it. The mass and charge of the electron and nucleus were measured by many people. Electrons can have different states with different energies. That is also a fact because of the atomic spectra. What else can we talk about the electrons inside an atom? Can we say that the electrons move on elliptic orbits or can we say that the electron inside a hydrogen atom has a speed of, say, 1000 km/s at this moment? No. Why? Do not forget “shut up if you haven’t made a measurement!” You may say, well, let us do a measurement on the position hence the orbit of the electron in the hydrogen atom. OK. How can we do it? If we have a super high resolution microscope, then we can look through it and find where the electron is and how it moves, right? Of course you are right. But how does a microscope operate? I know. It shines a beam of light on the object and receives the reflected light from the object you want to observe, from the reflected light we can see the object there. If you want to look at an electron, you beam light on it and see the reflected light. But do not forget that an electron is tiny and very light. When you shine a single photon on it, it is scattered away, perhaps to a place far from what it was before you beam light on it. Imagine you hit a billiard with a table tennis and make a measurement of the position of the billiard with the reflected table tennis. You know you can do it but you also know it would bring errors, sometimes disgustingly big errors.
This is the fact of life in microscopic world if you still adhere to one of the most fundamental principles in science “shut up if you haven’t done the damn thing.”
Because you have to do measurement before you dare to make a claim and because measurement may introduce uncertainty, you get different outcomes if you change the order of making two measurements, right? So the frightening statement “the order of making measurements matters” should become transparent now.
Two steps away and you are with quantum mechanics.
Step 1: How to describe this order of measurements? You are a smart gal. You say: just make a simple subtraction: see the difference between the outcomes with two different orders of measurements. Bingo! You got it. In quantum mechanics, we count the difference of the outcomes from different orders of measurements. If the outcome of measuring B before A is O_ab and the outcome of measuring A before B is O_ba, then the difference is O_ab – O_ba. That is the uncertainty caused by changing the order of measurements.
At this moment, a natural question you might ask is: Can this uncertainty specified? Or is this uncertainty measurable?
This leads to Step 2: The difference of the outcomes of the measurements of different orders is quantifiable. Heisenberg found the first such a difference. That is his famous principle of uncertainty which establishes the difference between measuring position before momentum and measuring momentum before position. His result is neat and beautiful: this difference is just the Planck’s constant (ignoring some constant). It turns out that his discovery is just one very simple, though very important, case. There are numerous physical quantities hence numerous ways of changing the orders of measurement. Each pair of physical quantities has its own uncertainty relationship. For instances, you may measure energy and time in different orders, you may measure x- and y-components of the particle position in different orders, you may measure the y- and z-components of the angular momentum of a particle in different orders etc. for each of these measurements, there exists a definite uncertainty relationship. For example, if we measure x- and y-components of the angular momentum of an electron in different orders, the uncertainty is also equal to the Planck’s constant (ignoring a constant). On the other hand, if we measure the x- and y-components of the electron position (characterized by three components x, y and z) in different orders, we get the same result. This means we may measure the two components simultaneously. Therefore, changing the order of measurement may or may not change the result. In symbolic language, you may denote the (generalized) uncertainty principle as AB – BA = Ch where h is Planck’s constant and C may or may not be zero.
If you are familiar with matrix algebra, you would immediately notice that if we assign each physical quantity with a matrix, then above uncertainty relationship becomes obvious because we all know that matrix multiplication may or may not be commutable, i.e, the commutator AB - BA may or may not be zero. Indeed, in history, it was Pascual Jordan, who realized that what Heisenberg was doing is matrix operations. Jordan insisted that all physical quantities in the microscopic world must be described by a matrix. Of course, matrix is just a dress of some more general thing, called operators. In other words, matrix is a special kind of operator.
Therefore, why we have uncertainty is because our physical quantities become operators at microscopic level. We can only obtain the ‘eigenvalues’ of these operators. Uncertainty is a consequence of the commutator of two operators. But this widespread notion is misleading. The correct way of stating it is: the uncertainty can be described with commutators. Therefore, quantum mechanics is not hard. It just quantifies a straightforward logic: doing measurements in different orders may produce different results.
Quantization is, in essence, to find the correct commutators that are related to different orders of doing measurements. Therefore, I won’t waste more spacetime on quantization because it is a profoundly simple procedure of counting the difference of doing measurements in different orders. It is not ‘the deepest mystery in science’ as you are frequently terrorized by crackpots. Quantization is nothing complicated although its significance is deep and far-reaching. We, frankly speaking, are still doing something not that different than what the physicists were doing 80 years ago.
Echoing the conclusion of 2.1, quantization is “think about the difference between making love before dating and dating before making love!”
Does that make human affection an operator?
Also try to figure out how these commutators relate to our very first question "why the accelarating electrons do not lose energy by radiation and fall into the nucleus?"
2.3 Fields and Quantum Fields (1)
To refresh your mind, I sum up the previous posting: quantum mechanics is a simple, logic, objective and truthful description of the microscopic reality. The most important rule we must follow is that ‘reality is the observed reality’, or ’reality is a body of information you could possibly collect on a system.’ To collect information, one must perform measurements. The order of measurements is of paramount importance and its consequence is neatly expressed with commutators. Therefore, any quantum theory ultimately boils down to finding the correct commutators. In this and next postings, I will extend this idea to fields, i.e., quantization of fields.First, answer to the final question of the previous posting: Because both the kinetic energy p^2/2m and potential energy, -Ze/r, are ‘time dependent’, if one looks at them individually, an electron in an atom does radiate energy. However, the total energy, after average over the state configuration (wave function), has definite, discrete values. This means, the radiation of the electrons inside an atom is self-compensated so that the electrons essentially do not lose energy (this becomes clear if one calculates the average of the nucleus-electron dipole moments over the wave functions of an atom in any stationary states-so called eigen states). Therefore, the peculiar commutation relationship between p and r renders the energies of the electrons definite and guarantees the stability of the atoms. In formal language, as a result of the commutation relationship between position and momentum, the spectrum of the energy operator has a limited, definite minimum. Spectrum reflects our spirit of ‘reality is reality only when it is observed.’ Had there been no such a commutation rule, the atoms would not have existed at all. How lucky we are in this universe where the microscopic world obeys quantum mechanical rules! Generally speaking, all bound systems have discrete energies, called quantized energies, or energy levels. For many bound systems, there exists a nonzero minimal energy, called zero point energy.
Now turn to the major topic of this posting—fields and how it is quantized.
Fields were introduced into physics by Michael Faraday. We know he was a scientist (physicist and chemist) of rarely high caliber. He was not formally trained and known to lack math skills, but few physicists in history left lasting influence on physics as he. In addition to great specific discoveries such as dynamo, electromagnetic induction, electrolysis, electroplating etc., he proposed the existence of electric field and magnetic field. He created such a great concept based on his experience and physics intuition: two electric charges may attract or repel each other even though there is only a vacuum between them. He hypothesized that there must be something very special between the charges, field as he called it. He also developed operational methods to measure the strength of the field.
However, the question of “what in the world is a field?” has been in the mind of physicists. In Faraday’s picture, field is a ‘special stuff’ generated by electric charge or electric current. For a long time, his idea was accepted without much further scrutiny. Anyhow, nobody could say better than that and nobody could understand what that ‘stuff’ really is. People adopted a kind of pragmatism and described a field as something generated by a ‘source’ or charge (such as electric charge, magnetic moment, mass, ‘color’ etc), added to the void or vacuum or nothingness or spacetime. Fields can be regarded as some medium in spacetime albeit a very, very special kind of medium. However, about 100 years ago, Albert Einstein showed that gravitational field causes a distorted vacuum or spacetime. Crazy enough, he told us that spacetime is the gravitational field itself. We will not mention gravitational field until in the last postings of this series. Before then, we just visualize spacetime as a vast void waiting for ‘things’ to fill in. But here I must caution you that vacuum in physics texts is very different from void or nothing. Vacuum must be understood as some extra stuff in void or spacetime. I hope you will eternally keep this picture in your mind after finishing this posting.
According to today’s fashion, fields are the most fundamental ‘being’. A vacuum is the ground state, namely the lowest energy state, of some being. Notice here, that we have different vacuua because the ground states of different beings can be (and should be as some people insist) different. Actually, from here we can sense something eerie about modern physics, but I do not want to distract you at this moment. We will come back to this subject later.
Therefore, at the most fundamental level of reality, we have fields and we have fields of many kinds. Vacuua are the lowest energy states of these fields and particles are the other states of the fields. In other words, particles are created as a result of field excitation. Take a violin as an example. The vacuua are the strings at rest and particles are created if the strings are pulled. The vibrating strings may affect each other when they vibrate in harmony. According to this picture, we naturally arrive at an important conclusion that interactions between particles are mediated by fields. In fact, fields and particles are the same ‘stuff’. Particles such as electron, quarks, photon, muons, mesons, are all ‘excited’ states of their corresponding fields. Although we tend to visualize these ‘particles’ as some tiny-whinny point-like billiards roaming around in spacetime, we know we must be careful not to go too far.
I can imagine someone now would jump and protest: “Aren’t particles localized in space and fields distributed throughout the space?” Great question. Now it is good time for us to review and apply quantum mechanics we learnt in the last posting. The most important lesson from quantum mechanics is those commutators. For instance, position and momentum have such a commutation relationship: xp – px = h (ignoring a constant). Translating this into a more operational language, we say that the position and momentum of an object cannot be measured precisely at the same time. For a point-like object, by definition, it has a fixed value of position, i.e., the position has a precise value. This means the momentum is completely indeterminate to keep the commutation relationship valid. This is to say that the position at the next instant is completely uncertain since we have no information about its momentum (hence speed). It could be anywhere in the universe. Or it is nowhere. What is this kind of object? Isn’t it just like a ‘wave’ with no specific position?
On the other hand, if we get a definite momentum of an object upon a measurement, its position would be completely unknown, i.e., it could be anywhere. Here you would not oppose that it is essentially a ‘wave’.
Therefore, you see, a ‘particle’ and a ‘wave’ in quantum mechanics are the same ‘stuff’. They are wave-particle or particle-wave or non-wave-particle or non-particle-wave, as you please. From now on, I hope you will get used to this picture that ‘particles’ and ‘fields’ are the same ‘stuff’. Forget old-time counter-revolutionary, totalitarian slogans such as ‘localized particles’ and ‘distributed fields’ and embrace new-age, revolutionary, democratic buzzwords such as “fields and particles are the equal” and “fields are particles and particles are fields”, ”Vauua are the fields at the lowest state or ground state and particles are the higher-energy states of the fields.” Brainwash yourself for as many times as possible.
In brief: spacetime + ground state of field --> vacuum --> particles are born when a field is excited. Particles are babies born from vacuua. Vacuua are embryos of particles. We have different babies, so we should have different vacuua. You would agree that it is a good idea to use the enlightening symbol |0> to denote a vacuum.
You may ask: “how a field is excited so that particles are created?” It sounds hard but it is sucking easy. To see this, again, the violin metaphor is helpful. You pull the strings and you excite them and you create ‘particles’. What does it really mean to say ‘to pull the strings’? It is simply putting energy into the strings. Physicists use a similar method to give birth to particles. They add energy to a vacuum and the field is excited and particles are born. In formal words to exert terror, they use something called creation operators, denoted as a’ where the superscript ‘ means creation. When a creation operator acts on a vacuum, a particle is created, i.e., a new state of the field is created, simply denoted as a’|0>. Essentially, creation of particles is just pulling strings, or adding energy to a vaccum. The equation |1> = a’|0> is just a shorthand record of “a particle is created after adding some energy to a vacuum.” Kindergarten kids can tell us how to work with quantum fields. To compute how much energy is added, you simply count the number of particles created.
Just like a violin string may stop vibration if it loses energy, the excited field, or particles, may lose energy and go back to the vacuum state. When this happens, we say particles are annihilated or destroyed. By symbols, we have |0> = a|1>. Creation and annihilation of particles, or excitation and de-excitation of fields, are daily life of quantum fields.
In quantum mechanics, we measure all kinds of physical quantities such as position, momentum, angular momentum and energy. In quantum field theories, we do the same, but some simplicity as well as some complexity come in when we deal with fields. As for simplicity, we count the number of particles as kids can tell us. As for complexity, we have infinite number of positions and momenta so we have to deal with infinite number of degrees of freedom. There is another complexity, the so-called relativistic invariance, which has to be postponed to the next posting.
Quantum field theories can be regarded as an application of quantum mechanics to systems with infinite number of degrees of freedom. Therefore, it is no wonder in quantum field theories, the same principle applies: the order doing measurements matters. Creation and annihilation of particles is the central theme in quantum field theories as mentioned earlier. Creation and annihilation operators are what we need to perform measurements. The commutators in a quantum field theory, therefore, may be denoted as [a’,a] = h (ignoring a constant). That, as you may instantly recognize,is just the commutation relationship lifted from quantum mechanics. Yes. quantum field theories steal or herit a lot from quantum mechanics. But why don't we simply call them quantum mechanics?
To answer this question, some new element has to be introduced and we’d better leave it for the next week.
I hope by far you have not been deterred. I promise that you will have an easier time in the future if you have come along without much agony. As long as we maintain some percentages of the curiosity and persistence of our chief scientist Shortriver Scholar, we will be able to climb up to the summit of modern physics.
Gauge Theories -2.4 Fields and Quantum Fields (2)
As usual, let us review the main points of the previous posting: fields are the most fundamental being of the reality. Vacuua are the lowest states of fields and particles are the excited states of fields. Consequently, particles and fields are the same stuff. Creation and annihilation of particles are just a graphic way of depicting energy input to and output from fields, respectively. The order of performing measurements on quantum fields is expressed with the commutation relationship between creation and annihilation operators.At this point, you should be able to properly answer the oft-asked questions such as “what is the size and shape of an electron?” and ”how can you be sure all electrons in the universe are the same?” etc.
No let us move on.
The previous posting concluded with this question: “since quantum field theories are just applications of quantum mechanics to systems with infinite number of degrees of freedom, why don’t we simply call them quantum mechanics?”
We will give a full answer to this question in this posting. Along the way, we will talk about relativity and why it has to be accommodated in a decent quantum theory. We hope this posting will also assist the reader to have a better understanding of the concepts introduced in the previous posting. After this posting, we will be able to introduce a set of new commutation rules, complementing the one we mentioned at the end of the previous posting.
First of all, we point out a trivial fact: the term “quantum mechanics” is normally used as synonymous with “non-relativistic quantum mechanics.” This is to say, ‘quantum mechanics’ used in most settings, does not consider the effects of relativity. “That’s certainly not good enough,” I can hear your blurting. A complete quantum theory must be consistent with the special theory of relativity and must be integrated with it. Such a quantum theory has a special name—quantum field theory.
Quantum field theory fulfills the mission of unifying quantum mechanics and special theory of relativity. According to Steven Weinberg, the master among masters, quantum field theory is the only logical consequence of quantum theory integrated with special theory of relativity (plus some other commonly assumed principles in physics). Quantum mechanics has to become quantum field theory if relativity is taken seriously. You may also sense that a quantum theory incorporated with special theory of relativity somehow necessitates fields. Yes, exactly. Fields become the most fundamental building blocks of nature once quantum theory and special theory of relativity meet, mingle and mate. If you are a curious guy, I’m sure you must be utterly intrigued at this point. A lot of people get completely lost here and at the same time desperately attracted to this seemingly unlikely twist because it sounds as if relativity plays some magic acts that turn the stage (fields) into protagonists. We should not miss the opportunity to enjoy the mental euphoria offered by the great quantum physicists.
I do not need to spend much spacetime talking about relativity theory because it is well known for being profoundly trivial. It can be loosely packed into a very short sentence: the speed of light is the same for any observers. It is always c no matter in which reference frame you perform the measurement. Suppose someone is moving at, say, 0.5c and send a beam of light forward, the other guy who is at rest measures the speed of light and he will get exactly the same value c, not c + 0.5c. One cannot add a speed to c. Why does light show such an odd behavior? Textbooks tell you that experimental results in electromagnetism say so. (But I believe there exists a ‘deeper’ interpretation and I challenge you to figure it out and post your answer here. I will show my interpretation in the next posting.) You can imagine that to maintain such a bizarre behavior of light, the rule for adding up speeds, i.e., the transformation rule from one reference frame to another must be a little bit different from that you see in high school books. That is Lorentz transformation, a simple algebraic expression even Einstein, well known for his math deficiency, could manage it properly after sweating on some trials and errors. So I do not need to waste spacetime to write down that transformation here. “Light does not change speed”, that’s all relativity theory about. The consequences of this deceptively simple statement, however, are somewhat counterintuitive albeit not mindboggling. The mostly referred phenomenon is that spacetime interval, i.e. the duration of a clock’s ticking and the length of a ruler, depend on speed. Motion shortens length and dilates ticking. It is actually a rather shallow conclusion if you must keep the speed of light the same in all frames of reference. If the ruler and clock do not behave differently in different reference frames, addition of speeds has to be just like ordinary arithmetic summation. Only by imposing a specific restriction on the frame-dependent ruler and clock, can light move at a constant speed in all reference frames. For example, the light in a moving frame might look traveling a longer distance as measured in the rest frame, but the duration the light travels for, measured in the rest frame, also increases by the same factor, maintaining the speed of light the same in both frames.
If you bother to take a look at the algebraic expression of the Lorentz transformation (I break my previous promise and show it in full here: x’=ax+bt, t’= ax + ct, y’=y, z’=z) that a kindergarten kid can understand, you may readily find that is just a rotation of a ‘rod’ in a four dimensional manifold. The length of the 4-rod is a constant. Relativity is absolutivity in the four dimensional (Minkowski) spacetime, as you may often hear. If you bother to take another look at the Lorentz transformation, then you’ll find the following slogan just crap: space and time are related to each other, not separated, to form a single four dimensional entity. (Experts know that space and time are already connected in ancient Galilean relativity.)
As a sideshow, I write a few more words further debunking relativity. It is a sad phenomenon that such a slim and simple theory as relativity is so gravely mystified, by both laymen and professionals. The spirit of relativity is actually exactly the same as that of quantum mechanics, i.e., reality is reality only after it is measured. We come to terms with quantum mechanics once we get rid of the ‘classical’ wishful thinking about physical quantities such as position and speed. We inevitably arrive at the special theory of relativity once we are serious about measuring distance and time duration. It is just another demonstration of the triumph of logic and realism. With this observation, I hope you are a little more empathetic to the fathers of quantum field theories who felt so compelling that quantum mechanics and relativity theory had to be unified.
One of the most conspicuous consequences of combining quantum mechanics and relativity is that particles may be created or destroyed. How does it come? A shortcut, widely used in popular books and formal textbooks, is that uncertainty brings about energy fluctuation which according relativity theory implies a fluctuation of mass hence particles. The shorter time one observes, the more particles are created ephemerally. Remember what happens when we try to measure the location of an electron with higher and higher precision? We need more and more energetic photons (so their wavelengths are shorter and shorter). But a photon of sufficiently high energy may transform into an electron-positron pair which in turn may create (and annihilate) other particles. Therefore, according to this picture, relativity requires creation (and destruction) of particles.
However, this picture seems not to catch the most important characteristic of relativity, i.e., spacetime is relative and governed by the Lorentz transformation. How quantum mechanics is integrated with a relative spacetime in a quantum field theory is unclear here. In other words, where in a quantum field theory is the concept of relative spacetime hired to play a pivotal role? We would better address this issue here. As mentioned before, the only math in relativity theory is the Lorentz transformation. A quantum field theory must observe the same transformation rule. That is called Lorentz invariance. Therefore, the integration of relativity theory into a quantum field theory is realized by Lorentz invariance. Therefore, you should not wonder all quantum field theories are born to be ‘relativistic’. Some unexpected consequences follow, such as that the probability of finding a particle is not an invariant anymore. In quantum mechanics, the probability of finding some particle in the ‘universe’ (some predetermined region) is conserved and can be normalized to 1 if needed. That is another way of saying that a particle would never disappear in the ‘universe’, or, a particle cannot be created out of blue. However, it is against what happens in a real world. Particles do disappear and particles do pop up as if from nowhere. For example, a photon can be absorbed by an atom and disappears for good. An electron can be absorbed by a proton or by a positron. A pair of electron and positron may be created from a high-energy photon. What amounts a little bit counter-intuitive is that the creation and annihilation of particles are a natural consequence of relativity. The requirement of Lorentz invariance on the dynamics of quantum systems not only permits, but demands, creation and annihilation of particles. You may have been told for billions times that relativity is far from human experience, but you now try to figure out why you can read and write in night under a light bulb. ‘Old quantum theory’ might tell you that an excited atom may radiate ‘spontaneously’ so you have light. But now you should understand that it is relativity that plays a background role for you.
Therefore, we learnt that particles can be created and destroyed as a consequence of Lorentz invariance. Particles living in the four-dimensional Minkowski world are not eternal, but ephemeral. Particles can be created and destroyed anywhere and anytime. This leads to the ‘fieldization’ of particles, i.e., we'd better simply assume that fields are the most fundamental ‘stuff’ filled in the spacetime and particles appear or disappear because the underlying field is excited or de-excited. Relativity, or more specifically, the Lorentz invariance, therefore, requires that quantum mechanics grow up to quantum field theory. Wavefunctions in quantum mechanics have to be upgraded to, or, replaced by, fields. ‘Finding a particle at position x’ in quantum mechanics has to change into “excitation of field at position x’. The notion ‘a particle disappears at position x’ is illegitimate in quantum mechanics, but the notion ‘a particle is annihilated at position x’ makes perfect sense in quantum field theory (and conforms with reality for sure). The reason of introducing creation and annihilation operators becomes obvious.
Relativity also leads to another crucial and striking consequence: for every particle, there must exist an anti-particle which has exactly the same rest mass and spin but with opposite charge of the original particle. To see this, we recollect how to excite a field and create particles. A field is excited if an adequate amount of energy is added into it. A particle is created somewhere and sometime in spacetime. Quantum mechanics tells us that we have uncertainty to specify precisely ‘somewhere and sometime’. This means we do not know exactly where and when the new particle is created. In quantum mechanics, we want to compute the ‘evolution’ of a wavefunction and that can done by calculating the Schroedinger equation, the equivalent of Newton’s law in classical mechanics. In particular, we need to compute, given the value of the wavefunction at some initial time t0, what is the wavefunction at some later time t. This is an exactly the same procedure in classical physics where we are normally asked to compute the position of an object at time t given the position at x0 at time t0. In classical physics, we have trajectories, the history of the positions. In quantum mechanics, we do not have trajectories and we only have probabilities. Therefore, in quantum mechanics, the ‘evolution’ or ‘prediction’ problem changes into “finding the wavefunction at time t.” That is equivalent to “finding the correlation of wavefunction at any time t and that at an initial time t0.” Correlation function (of wavefunctions) is not only easier to compute in many cases, but also can be directly extended to quantum field theories. Actually, the same strategy can also be employed in classical physics to increase computing efficiency and in many circumstances offer invaluable insights. (It is categorically called Green function method.) In quantum field theories, therefore, the primary goal is to find the correlation functions of the creation/annihilation operators. All calculations in quantum field theories boil down to computing these correlation functions. In quantum mechanics, the correlation function may show space-like characteristic, i.e., faster-than-light propagation (‘spooky action at distance’ as Einstein bitterly called it) is allowed in quantum mechanics because quantum mechanics, as we mentioned earlier, is supposed to be non-relativistic and does not observe the constraint of relativity. Quantum field theories, however, are born to be relativistic and must not permit such space-like correlations. Since particles are created or destroyed at random positions and instants, space-like correlations are intrinsically and inevitably present in quantum field theories. On the other hand, relativity theory is by no means violable. Therefore, the ball is in the court of the quantum field theory. An acceptable quantum field theory has to get rid of this ‘spooky action at distance’to marry with relativity. This, it turns out, is not an irrational demand, but a fortuitous blessing. After some struggle, physicists came to a perfect, or ’more perfect than perfect’, solution to this conundrum. If for every particle, an anti-particle, with exactly the same mass, spin but with opposite charge, is introduced, then the annoying ‘spooky action at distance’ disappears. The space-like correlations caused by the wanton hide-n-seek games played by the particles are exactly cancelled out by the same tricks played by their respective antiparticles. Don’t you think this is a one-stone-for-two-birds solution? This kind of elegant combo show of the human’s intelligence and Nature’s beauty is rare in the history of science and is never overpraised.
Textbooks may tell you that antiparticles guarantee an important constraint on the speed of information propagation: no information can be transmitted faster than the speed of light. In formal language, the space-like propagation (a shorthand notion for faster-than-the-speed-of-light signal transmission) is zero if antiparticles and particles are on the same footing in a quantum field theory. However, it remains a debated issue whether information propagation speed is the cause of antiparticles or antiparticles are the cause of information propagation speed. Most textbooks do not bring up this question but it is an interesting and worthwhile question. Yours sincerely prefers the former but some authors prefer the later. You make your own decision and you are safe, so far, at least.
Some people may tell you that antiparticles are just ‘holes’ in the vacuum, running backwards in time, but that notion, heuristic and entertaining as it may be, can be catastrophically misleading. Besides introducing the unphysical concept of ‘negative time’, this makes an antiparticle look surreal and even imaginary, but we know that for a given field, who is given the name particle and who the name antiparticle is completely arbitrary. Indeed, the formulation of a quantum field theory dictates that particles and antiparticles are on exactly the same footing. For the reader who is familiar with Fourier analysis, antiparticles in quantum field theory pop up as naturally as the ‘negative frequency’ components appear in a ‘signal’. It is only for the sake of custom and convenience that we specify which frequency is positive and which is negative. When a field is excited, both positive and negative frequencies are necessarily created, exactly the same as when a desk is pounded or the floor is stamped, both positive and negative vibrational frequencies are equi-probably generated. Therefore, you see, nothing mysterious and nothing hard about antiparticles. They have to be there and have to be taken into account.
Before concluding, we mention that the notion of particle is not a watertight concept. For example, you may ask: can I decompose a field in a different way other than Fourier expansion? Sure, you may. And you should. That’s why you heard of pseudo particles, quasi-particles and virtual particles. For example, a virtual particle is something like a wavelet rather than a single-frequency component (ordinary particle). A wavelet may have many different frequencies and contain a decay factor (equivalent to having a finite lifetime). Indeed, we still have some open questions about ‘particles’. We will come back to this point in due time.
With the preparation of this posting, we will be able to come back to our earlier assignment—the commutators of quantum fields.
2.5 Fermions, Bosons and Anyons
First I apologize for not being able to write this series in most of the past month because of some unexpected assignments. I appreciate the readers, the great Scholar Shortriver, in particular, for their patience.In the previous 2 postings, we have learnt that quantum field theories are the natural, necessary and indeed inevitable outcome if quantum mechanics has to be incorporated with the special theory of relativity. In passing, we were also told that antiparticles are a must for quantum field theories. With antiparticles, the notion that “particles and fields are the same stuff” becomes more transparent: fields are the configuration of a physical system in the real space and particles are the fields in the momentum space, or, k-space. Fields and particles are just two different but equivalent descriptions of nature.
What I did not mention is that the inclusion of the special theory of relativity has another ‘deep’ consequence: the particles and antiparticles, or the excited states of the field, have internal degrees of freedom. For instance, a particle may carry spin, or magnetic moment. It is well known that the electron has a negative charge, but it is less well known that the electron also has a magnetic moment, i.e., an electron is a tiny bar magnet. The fact that an electron has a charge is the foundation of the mature electrical and electronic industries; the fact that an electron has a spin is the foundation of the emerging technology called spintronics. In the following, we will reveal the fundamental origin of this internal degree of freedom. With that, I hope you will have a better and deeper understanding of our spacetime and the fields/particles it permits.
Now we are in the position of ending the conceptual introduction of quantum field theories by presenting all the commutators related to quantum field theories. We were informed at the beginning of Section 2 that all computations in quantum field theories, such as in particle physics, nuclear physics and cosmology, boil down to the manipulations of commutators. Now that we have antiparticles, we need to introduce the corresponding creation and annihilation operators, b’ and b. To include antiparticles in quantum mechanics, we need to stipulate the difference between doing measurements in different orders, i.e., we need to specify new commutators for b, b’ as well as between a’, a and b’, b. The idea is exactly the same, only more lines of formula are written.
Experience tells us that even for one type of particles, they may be different physically, namely they may take different values for a given physical property. That is of course obvious. An electron, for example, may have different kinetic energies, momenta or spin. It is convenient in practice to use extra subscripts to specify these properties and creation and annihilation operators now look like a’_i, b’_j, a_i, b_j etc. The most important gadgets in the entire toolbox of the quantum field theories are the following commutators: [a’_i, a_j], [a_i, a_j], [a’_i, b’_j], [a_i, b_j], b’_i, b_j], [b’_i, b’_j], [b_i, b_j]. What more happy is, most of them are simply zero. For instance, they are all zero if i is not equal to j. Similarly, any pair creation operators and any pair of annihilation operators are zero. These facts are easy to understand in perspective of viewing a commutator as doing measurements in different orders.
The only nonzero commutators are [a’_i, a_i] = h and [b’_j, b_j] = h (ignoring a constant). In words, the following two cases have different outcomes and the difference is characterized by the Planck’s constant h: (i) creation of a particle before its annihilation and (ii) annihilation of a particle before its creation. In case (i), the particle has not existed yet, but in case (ii), the particle has already been there. Therefore, a quantum field theory is not that different from quantum mechanics. It is still about measurement albeit on systems with infinite number of degrees of freedom. The commutation rules are not much different from those in quantum mechanics. The only spectacular thing, as it seems, is the introduction of antiparticles imposed by the special theory of relativity.
Is it the end of the story?
Unfortunately, it is not. No. Fortunately, it is not.
It turns out that the above commutators only apply to one class of particles called bosons. The other class of particles, called fermions, satisfy a slightly different commutation rules, i.e., anti-commutation rules: {a’_i, a_i} == a’_i a_i + a_ia’_i = h. That is to say, the minus sign in a commutator has to be changed into the plus sign for fermions. The reason is that bosons and fermions have different internal degrees of freedom: bosons have an integer spin such as 0, 1, 2,…while fermions have a half-odd-integer spin such as 1/2, 3/2,...
Why is it so? Why do we have two classes of particles? Or why do we have two classes of excited states of the fields? The question can also be askedin this way: Why do we have ONLY two classes of particles? The root of cause is that our fields are “contained” in spacetime. We all know that a container necessarily imposes some constraints on its content. The oil in a capillary and the oil in a film on the surface of, say, water, may show very different properties. The properties of spacetime must affect the properties of the fields it contains.
From the Lorentz invariance we learnt in the previous posting, we know that our spacetime is isotropic or democratic, i.e., there are no noble positions and times nor autocratic directions. It seems a really plain, unremarkable, even boring, fact of nature, but it is one of the most important facts for physicists. Imagine that our spacetime does not have this symmetry. Then this would imply that every point of our spacetime has its own physical laws, possibly unrelated, or, related to each other in a very complicated manner. Billions of Newtons and Einsteins would not be sufficient to find a physical theory applicable to our universe!
Fortunately, our spacetime does have this beautiful, simple symmetry (at least a very good approximation). A completely democratic spacetime has the highest symmetry as you can see it immediately, denoted SO(3) or SO(3,1) if time is also included. That is the most important property of our spacetime. Understandably, we will come back to this group frequently.
It is this obvious property of spacetime that leads to the two classes of particles, or, two sets of commutation rules (commutation and anticommutation rules).
To pinpoint which property of spacetime determines the commutation rules, we take a closer look at the meaning of a commutator, the symbol denoting the difference of doing two measurements in different orders.
In the language of ‘particles’, for a system consisting of identical particles, exchanging any two (or more) particles should make no differences. A country full of identical individuals would not make any difference if any two of them exchange positions. In quantum mechanics, this means that the exchange of any two particles should not make any measurable effect, i.e., it is of no significance on any measurements. However, we must be aware of that no effect on measurement results does not require no effect on wavefunction or field configuration. As mentioned in Section 2.2, wavefunction is more a supporting tool to assist calculations than a physical object. In fact, as well known, if a wavefunction is multiplied by a phase factor ph=e^(i*theta), no physical difference is made. So is the case for field operators. Therefore, if two identical particles exchange positions, the wavefunction or field operators may be changed, at most, by a phase factor. Any two particles can exchange positions and bring a phase factor to the wavefucntion or field operators. Because of the equivalence between particles and fields, the effect on exchange in positions is exactly the same as that on exchange in momenta.
Therefore, the effect of exchanging particles on creation or annihilation operators brings about, at most, a phase factor, i.e., the general commutation rule, after taking this identical symmetry into account, is: [a’_i, a_i*ph]=h. It might be superfluous to mention that this identical symmetry is a consequence of our isotropic spacetime. The remaining job is to find what this phase factor ph is. As mentioned above, this ph must be a property of our spacetime.
[a slightly different way of argument: an identical particle system should possess exactly the same symmetry of the spacetime. the wavefunction of a particle under a full rotation (e.g., a 360-degree rotation around a fixed axis) must show no difference other than a phase factor. therefore, when two identical particles are exchanged, the effect is at most a phase factor. it is equivalent to say that change of the order of any two creation/annihilation operators, brings about at most a phase factor. ]
Well, exchange of two particles produces, at most, a phase factor. How many different values can ph take? The problem, therefore, turns into how many distinct ways we bring a system back. It seems we have an infinite number of ways. However, our spacetime has a high symmetry, specifically its symmetery group is SO(3,1). Among the seemingly infinite number of ways of bringing a system back, many of them may be identical. To see whether two ways are identical or not, we look at the parameter space of the symmetry group. A rotation is specified by the rotational axis and the angle of rotation. It can be expressed by a point in a space: its distance to the origin is the rotation angle and the direction of the vector linking the point and the origin is the rotational axis. The parameter space of a symmetry group is the collection of all such points. The parameter space (topological space of the symmetry group) of SO(3) is a ball with diameter pi. Considering the rotations of pi and –pi are identical, all antipodal points of the surface of the ball must be identified.
A loop (with its base point at the origin) in the group space corresponds to a series of transformations that return the system to its original configuration. If two loops can change from one to the other via a continuous deformation, they are equivalent. Two equivalent loops make no difference on the system. In particular, if a loop can shrink into a single point in the group space, the transformations are equivalent to a single rotation. If a loop can shrink into the origin, the transformations are equivalent to no rotation at all.
How many ways of shrinking a loop in the parameter space of the symmetry group of our spacetime? For the topological space of group SO(3,1), it turns out that there are only two classes of loop: A loop in the group space that can shrink into a single point (the origin) and a loop that cannot shrink into a single point but two of such loops can shrink into a single point. We find that the loops in the parameter space of the symmetry form a group, called the fundamental group. For SO(3) group, therefore, its fundamental group has only two elements: the class of loops that can shrink to the origin and the class of loops that need run two turns to shrink to the origin. The first class corresponds to ph=1 and the second to ph = -1. Taking into account the symmetry of spacetime, therefore, we find that there are only two possible distinct effects on a system by exchanging the particles.
In formal, concise language, the commutation of creation/annihilation operators is decided by the fundamental group of the topological space of the symmetry group of the particle system. It may sound bizarre for the people who hear this for the first time, but do not worry. Here we add a paragraph to dispel the mystery of the fundamental group. The reader who is already familiar with the group space may skip the following paragraph and simply jump to the last paragraphs of this posting.
Let us take another look at what is the topological space of a (symmetry) group. The symmetry group itself is a topological space, i.e., the space formed by exhausting the values of the parameters that characterize the group. For example, the symmetry group of a circle is SO(2), i.e., the circle shows no difference when it rotates around its symmetric axis by any angle. The parameter space of the symmetry group, therefore, is a real line. However, we know two more facts about rotation around a fixed axis: (i) that rotating by alpha is the same as by pi – alpha, (ii) rotating by one turn is the same as by any integer number of turns. Taking these two facts into account, we find the topological space of SO(2) to be something like this: a line but we have many, many equivalent points, such as (using pi as unit): 1 = 2 = 3 = 4 = …. n = -1 = -2 = -3 = …. = -n and a = 1 – a. Therefore, the parameter space of SO(2) is a segment [0, 1] with its two endpoints 0 and 1 identified (equalized). It is actually a circle. The group space of the group SO(2) (the symmetry group of a circle) is a circle. It is easy to find that the loops (of any turns) on a circle cannot shrink to a point. Any two loops of different turns belong to different classes. Therefore, the loops form a group with infinite number of classes (elements). The fundamental group of the topological space of SO(2) is all integers because any number of turns around the circle is different from other numbers of turns. This has a profound consequence: the exchange of any two particles in a 2+1 spacetime can bring about any phase factor ph. The commutation rule for the field operators, therefore, is the most general form: [a’_i, ph*a_i] = h. The particles satisfying this rule are called anyons.
In summary, the fundamental group can be simply described as the ways of contracting a loop in the space. Visually, the fundamental group identifies the ’holes’ in a space. The fundamental group of the topological space of SO(3) is a group with only two elements (denoted Z2) because there are only two different ways of contracting the loops in this topological space. For two-dimensional systems such as the electrons restricted in a film or bound in a membrane, the symmetry group is reduced to SO(2) whose fundamental group has infinite number of elements (Z). In our spacetime, i.e, 3+1 manifold, ph=+1 for bosons and ph=-1 for fermions. For 2+1 spacetime, ph can be any values and the corresponding particles are called anyons. Therefore, the commutation rules in quantum field theories have a deep origin that traces all the way back to the most fundamental properties of our spacetime, the topological structure of the symmetry group of our spacetime. Doing measurements in different orders must consider the symmetry of our spacetime.
Therefore, the topological property of the spacetime may provide an extraordinary restriction on the possible types of fields or particles. For 3+1 spacetime, there are only two types of particles. We may assign an internal degree of freedom, the spin, to the particles. In this picture, the commutation or anticommutation is decided by the spin of the particles, integer spins (bosons) obeying commutation rule, half-integer spins (fermions) obeying anticommutation rule. For 2+1 spacetime, however, an infinite number of types of particles may be allowed. Non-integer and non-half-integer spins (anyons) obey ‘any-commutation’ rule.
There is another way of describing above difference. According to the special theory of relativity, a particle can be described by its worldline—the “trajectory” of the particle in spacetime. The history of a particle can be represented by a curve in the spacetime. You may imagine that the worldlines of the particles form noodles or braids. Exchange of particles means the braids getting tangled. In 3+1 spacetime, the tangle by exchanging the worldlines of two particles can always be detangled. In 2+1 spacetime, however, the tangle cannot be detangled.
Now it is good time to upgrade our old picture of spacetime as a kind of passive, void background or box detached with the fields or particles it contains. In the previous posting, we learnt that the special theory relativity tells us that spacetime is not a passive framework, it has its unique property: it obeys Lorentz transformation rather than Galilean transformation, i.e, space and time are connected. In this posting, we see that the topological structure of spacetime provides a severe restriction on the possible types of particles.
At this stage, we have come to the end of quantum field theories, conceptually. The remainder is technical. We may ignore them completely without affecting our understanding of nature significantly. However, to expose the problematic aspects of modern quantum field theories, we would better go through some technical procedures. The good news is that we still do not need equations to accomplish the job. Words, logic and a fresh mind are all we need here.
开心学数系列 Playing Math Series
闲论Atiyah-Singer指标定理Nowadays, mathematicians tend to over-abstract things that in fact cannot be further abstracted, which not only dilutes the essence of concepts but also drives away potential students and users, and eventually, if this pathological mood is not cured, will make a lot of mathematicians breadless. ---------Vladimir Igorevich Arnold
开场白
余观天下学数众才,体察愈久,遗憾益多。开始决定献身数学时,大家都是聪明、愉快、可 爱、活泼的,也是被别人视为天赋才俊。但是随着时间推进,一些人开始变愚蠢了,一些人 开始变苦闷了,一些人开始变得令人讨厌了,一些人开始变古怪了,一些人变虚弱了。更过 一些时间,一些人已经是白痴了,一些人已经自杀了,一些人已经是罪犯了,一些人已经是 疯子了,一些人累死了。现在走在这条路上的或朝这条路上走的仍然是千千万万,各种悲剧 天天发生。身是献了,但白献了。还搭上翘首期望的家人亲友以及一些无辜的关连者。 万幸偶有小成大成者,却同时也惹出一堆冤家对头,倾扎之惨烈,不亚于黑帮火并。暂时胜 者担心报复,除时时努力固守城池以外,也终日疑神疑鬼,久而变态失常,最终众叛亲离者 绝非鲜见;一时败者则卧薪尝胆,时时司机反扑,报得一箭之仇,然现实常常是仇难报,气难 消,遂焦躁不安,怨天尤人,久而变得古怪,抑郁,甚至崩溃。 为何开始看起来的一桩好事会变得这样惨呢?主要是态度不对。古人练功修行讲的德字主要 是就是讲态度要正确。现在很多人,由首先喜欢数学崇拜数学变成拿数学当商品工具谋名获 利,并以所得多少作为衡量成功与否的标志,多数人因此走入歧途是必然的。正确的态度是 你玩数学或你与数学玩。以玩得开心为最高宗旨。既不要想通过学数学抱得美人归,住进黄 金屋,做得人上人,也不要想去光宗耀祖,恩泽乡里,更不要想去当所谓英雄为民族争光, 报效国家,这些人充其量也就是被权贵玩来摆去的宠物狗。如果一开始就是以正确的态度学 数言数,玩数之人就会永远保持聪明、愉快、可爱、活泼。如果是这样,我们看到的数学文 章着作也决不是现在这样以狗狗互相威聂的方式写成声明书。
本文题头引用的数学物理大师也是教育大师Arnold的话,反映本人对数学(物理)界悲剧的 另一些观察是也没有错误的。数学生到大二左右,就开始幻想脱离俗家尘世,进入不食人间 烟火的状态。先是与"土得掉渣,难以启齿"的具体数字和图形决裂,然后是大胆抛弃"半土 不洋,肤浅得很"的运算和公式,匆匆穿上光鲜的水货衣服(半懂不懂的外文书),擦上廉 价的胭脂(网上抄来的作业),配上借来的首饰(一知半解的老师讲义),端着身子急急溶 入"豪华典雅,宛如仙境"的各种抽象定义引理定理建构的"上流社会"。但是,正如Arnold指 出的,不必要的抽象不但害人,终将害己。与学武功的人类比,过分抽象等于过份强调虚力、 意志和策略而忽视实力、环境和具体的战术,好多从数之人走向悲剧,不光做不出数学成果, 最终连一份谋生的差事都做不来,重蹈邯郸学步覆辙,实属自取其果,如果一开始就加以注 意,完全可以避免。
鉴于上面几点,本文的第一个主要目的当然是要向外行以草包大众喜闻乐见的方式介绍一些 常人望而生畏的着名数学难题,作点破除迷信,奚落权威的事。旧时艰涩书中物,进入平常 百姓心,翰林神道华山剑,屠狗之辈亦善玩。既向有数学兴趣的人展示绝大多数的抽象是不 必要的害人之物,另外也顺便将一些所谓的"高度抽象"概念之唬人外表揭穿──世上无神鬼, 都是人炒起也,跟着抽象起哄的数学家中真正懂得实质的人并不多,与江湖郎中一样。本文 另一个主要目的之一是(向数学家们或数学家们to be)示范如何以正确态度学数学,如何 以正确态度讲数学。看看我如何讲数学,如何理解数学,希望给学数同道树个榜样。希望你 们读完此文以后,不光是具体知识增长了,学数教数的态度也变得积极正面一些,个人生活 变得快乐一些,减少悲剧的发生。方老师多年来以通俗的语言向普罗大众介绍现代生医,教 我们识别害人的巫医毒药,教我们保健养生,功德无量,不可磨灭,经济价值和社会意义, 则更无法估价。我辈应以他为楷模。其实方老师作功德的同时,也对自己的生活品质的提高 有很大的帮助,所谓助人者幸福,助人者天佑。我写此文也完全是本着渡人利己的原则,因 此,看官倘有收获,不必说谢谢,我已经收获了大头在先。
目录(subject to changes)
开场白
闲论Atiyah-Singer指标定理(1)─引子
闲论Atiyah-Singer指标定理(2)─雅俗两故事,AS的实质
闲论Atiyah-Singer指标定理(3)先声─Riemann-Roch与Gauss-Bonnet-Chern
闲论Atiyah-Singer指标定理(4)─黑话破解,主要概念介绍
闲论Atiyah-Singer指标定理(5)─奇径通峰,AS之证明
闲论Atiyah-Singer指标定理(6)─回味无穷,总结与教训
闲论Atiyah-Singer指标定理(1)─引子
Atiyah-Singer指标定理,江湖黑话谓之AS。它集映射,流形,纤维丛,特征类,上同调,椭 圆算子,Bott周期,范畴,K群等名草贵药于一丸,坊间流传,其外形神秘可畏,内在艰深 难测。它作为一粒神丹,用得好,据说它能立解万毒,有还魂回阳之功;用得不好,七窍流 血,凌迟而亡。另一方面,它又融微分几何,拓扑学,微分方程,代数几何等神刀鬼剑于一 体,有幸亲眼目睹真身者皆曰:阴森冷峻,杀气腾腾。它作为一件兵器,使得好,所向披靡, 固若金汤之城池不攻自破,平常骄王悍匪,纷纷挂表求降;使得不好,手抖脚颤,心慌意乱, 迷魂丧智,以自宫了结。
西域数坛崇AS为20世纪数学的之里程碑,中土学数者则赞其为泰山颠峰,东海之底,景仰之 情非科学者所能言表。数学科班出身者对之多谈虎色变,敬畏万分,偶被论及,或胡诌乱侃 吓唬外人,或顾左右而言他。理论物理诸生则视其为峻岭奇峰,跃跃欲试以领略身临绝顶俯视 众山之快感。然意欲登攀者,多数在此摔得身残心碎,从此一厥不振,消隐红尘,更悲者则 是落得粉身碎骨,抱恨终天。少数登高而成吸得仙风获此宝器者,则耀武扬威,不可一世, 每置对手于死地,更赖其奇功在江湖上呼风唤雨,坐定上排交椅。 如此神妙之仙丹,是谁炼成?如此威风之兵器,是谁铸就?倘真如上所述,则发明者功高胜 天,非溢誉也。 抑或果真有所称之奇妙威风?无有明夸暗炒之嫌? 且看polik慢慢贴来。
闲论Atiyah-Singer指标定理(3A)─椭圆算子与纤维丛(polik)
至少有些响应。感谢Berkeley狼,xj等人释疑,你们今年必有好运。
人终究是自利的。越写越觉得是娱己胜于娱人,以致有些地方突然变成自言自语。还有就是, 虽然我做了一些努力,一些术语的使用还是不符合中文数学文献之规范。这些只能请看官多 包涵。今后有空有兴再贴个修改版。
一开始提了,本讲座不是写给娃娃的童话,而是以领略数学颠峰奇景为目的,专门撩拨数学 里的超级成人话题,极黄极暴力。看官倘若没有疑虑、心跳、罪恶感以及愤怒的话,阁下必 定是数学狂魔,而且是绝代混蛋,数界的陈冠希们会上门跪拜求教。不过看官放心,多数疑 问到后面会慢慢澄清,到达顿悟是突然的,不可预测的,但只要稍有耐心它又是必然的。 那就继续讲集合、算子。 一类研究得比较充分的线性映像是线性微分算子。简单而言,线性微分算子就是一阶,二阶, ...导数拼凑成的算子多项式:
a_(n) f^(n) + a_(n-1) f^(n-1) +...bf
这里a_(i),i=1,2,...,n以及b都是x的多项式。看官可以验证一下,它满足线性映像条件。 假如f是多个变量,x_1,x_2,...,x_n的函数,则上述方程推广成n元微分算子多项式方程, 显然这种微分算子包含对单个变量x_i,i=1,2,...n的(1,2,...阶)导数,也包含对不同变量 的交叉导数,而每个导数的系数,写成一般的表达式为:a_(i_1,i_2,i_3,...),
i_1+i_2+i_3+...=1,2,...,n,它们都是x_1,x_2,...x_n的多项式。
正如代数多项式的根是代数学的基本问题一样,算子多项式的"根",即给定空间上的微分方 程之零频解问题,是微分拓扑学里的基本问题,简单地说也就是一般空间上的偏微分方程 (PDE)求解问题。
正如一元二次方程ax^2+bx+c=0按判别式b^2-4ac=正、负、零分别对应两实根、两复根、重 根的情况一样,PDE也依系数之关系决定解的差异,因而有抛物算子、椭圆算子、双曲算子 等之分。PDE的判别式由通过叫象征的东西给出:简单而言,就是将要解的PDE转成其富里叶 形式,
a_(jn) ξ_j^(n) + a_(n-1 k) ξ_k^(n-1) +...bξ
将其按x和ξ的幂次之和归并,最高次微分项最重要,故用其系数a_(jn)拼凑出n×n主象征 (矩阵)。主象征矩阵是对称的。比如二次PDE的主象征矩阵是2×2,三次PDE的主象征矩阵 是3×3...依主象征矩阵之正定,零和负定分别给出椭圆,抛物和双曲微分算子。 因此,椭圆算子定义为:如果微分算子主象征矩阵之行列式非零(主象征矩阵有逆矩阵), 则为椭圆算子。
我们做几个小练习。df/dx-df/dy=0和df/dx-idf/dy=0是两个看上去相当像的微分方程,但 它们的解的性质却大相径庭。第一个解是平庸的,第二个解是解析函数,拥有极丰富的内涵。 从它们的(主)象征:ia – ib 与 ia + b看,很清楚。第一个方程的象征在a=b时都会为零, 而第二个仅在a=b=0时才会为零,故第二个方程是椭圆型的,而且只有一个解,其解空间是 一维的(椭圆偏微分方程拥有有限维的解空间)。
看官可以亲自验证,通常向量分析里的梯度,散度和旋度算子都不是椭圆算子。 同理,也可以判断出物理上常用的拉普拉斯算子(Laplacian)是椭圆算子,因为其象征为 - a^2 - b^2,而另一个常用的达朗贝尔算子(D'Alambertian)必须限制在光锥外才是椭 圆算子。
我们考虑紧致流形,紧致大体就是有限的意思。泛函分析可以给出简单的定理:紧致流形上 的椭圆算子之ker和coker都是有限维的,即所谓Fredholm的。前面讲过,对于算子或映射 D: V --> W,coker = W / im D。dim coker不等于零就说明存在D不能映到的地方,也就是 说在W上存在额外的限制条件或约束条件。所以,对紧流形,椭圆算子自动暗含它就是 Fredholm算子。一般解析指标:ind_ana = dim ker D – dim coker D.
至此,可以解释所谓"微分算子解析指标是个拓扑不变量"是什么意思了。就是指算子里的主 象征矩阵元作连续变化时上述解析指标ind_ana不会改变。或者说,有无限多个PDE的解析指 标相等(虽然他们的解的具体形式会有差异)。AS定理告诉你这个值是该微分算子作用的流 形的拓扑性质所决定(难怪与主象征参数变化无关!)。AS定理也告诉你如何具体算出这个 指标的值,也就是说到底是流形的哪个拓扑不变量对应那些(无限多个)椭圆算子的解析指 标。
好,集合与映像联合王国的基础概念就暂时介绍到这,其实也没有太多别的啦。如果到此你 还没有产生恐惧感,我认为你绝对有起码的数学天赋,品尝几口21世纪数学饭馆的酒菜还是 受得了的,甚至能够尽情玩乐享受一番。下面讲一个具体的集合的例子,跟本主题有关的空 间,即纤维丛。
描写变化的函数,如车辆飞机的路线,股票的涨落,影音讯号,都是用平面曲线记录的,因 此,X-Y坐标系人人会读,人人要用。其实带坐标系的二维平面就是一个纤维丛。我们可以想 象整个平面是一根Y向直线横扫X空间而形成的。被横扫的空间(这里是X)叫底空间,那根 直线就是纤维。
从另一个角度看,我们也可以将XY平面当作一个乘积空间,即每一个X点可以与Y的每一点相 乘得到一条直线。
当然这是一个太平庸的例子,但一般意义的纤维丛确实是乘积空间的推广。"推广"了什么? 刚才的例子之所以叫平庸,是因为他每个地方的乘法完全一样,不同X的地方的Y直线毫无差 异,就像红朝人民的脑袋,万众一心,平庸得可怕。总而言之,一张四平八板的纸片确实有 点无聊。不过,稍微变一下就可以别开生面,例如,将纸带扭一圈或几圈以后对接,形成 Mobius带子。哈!你没办法用简单的坐标系或通用的乘法了。局部看来,小人度腹,依然是 个"平面方形",直线段尚在,依然可以用乘积空间描写,但稍微走远一点就发现,原来的"Y 直线"整条都是直的而且对得很齐但现在"弯掉了",不对齐了。跳出三界,来个全观,则发现, 相邻的弯掉的直线之间的关系(转换函数或联络)与扭曲的程度有关。 简言之,底空间各个地点各有各的纤维空间,就是非平庸丛了。
为了对阁下负责,对底空间,要做点补充。
第一是底空间无须平直,可以弯折。这个不奇怪,地球表面,阁下的俊脸贵体,都是弯曲空 间。不弯还不行。没有曲线美。问题就大了。
第二,空间的长度单位(标准尺)可以随位置甚至时间而变,即,各个地方的长度单位还不 一样(上海的1尺是广州的9寸)。这就是最通用的黎曼空间了。黎曼提出这种空间60余年以 后,爱因斯坦找到了一个物理实例(使之成为最伟大的科学家),也就是阁下所在的宇宙, 其实就是一个黎曼空间。真是不识庐山真面目,只缘身在此山中。当然阁下想看到尺子钟表 不一样,或者看到时空之弯曲,您得稍微走高一点看才行,例如走100万光年回头看。藉助 现代仪器如原子钟,地面与卫星轨道的时间差异就可以量出来。这里终于搭上了短江兄的GR 话题。
这有个休息亭,好,歇一会:一些人觉得像流形、非欧空间或弯曲空间难以捉摸,这里试着 从一种特别的角度解释一下。我们回顾一下微积分干了什么。依我看,其实就是用古希腊数 学家们关于线段、长方形和长方体的已知结果(长度、面积和体积)用来量度一般曲线、曲 面和曲体的长度、面积和体积。其中用到的一个基本假设就是,不管多么"弯曲"的东西,总 可以找到一个足够小的尺度,在此尺度下一切都是平直的。故可以用大量的微小线段、微长 方形或微长方体为"尺子"拼凑出任意的形状或体系。微分几何的大部分也就是告诉你如何用 微小的平直空间来建造一个"任意的"流形,所以基本思想还就是那一点东西在兜来兜去。 非欧空间简单讲就是一个到处充满奸商政痞地头蛇的国度,尺度和时间或物价等标准(数学 家叫度规)由这些地头蛇制订。经历千万年演化,这些地头蛇现在都成了蛇精,变态已极, 弄得流形上每一点都有其自己的度规标准,成语"点化成精"得改成"精化成点"。对于一个生 活在这个国度的人而言,弄清各个地头蛇之度量时间标准之兑换率是至关重要的,这个兑换 率就叫做联络(系数)。有人可能会讲,度规确定联络系数,简直是一句废话,纽约(N)一 美元是波士顿(B)的95美分,联络系数当然是L_{NB}=1.05或L_{BN}=0.95。大体没错。不 过,你们可能还不知道这些地头蛇有多么无耻变态,原来,"上海的1尺是广州的9寸"只是一 个大体的说法。地头蛇说,真正的兑换率还要看你的尺子是朝南北方向量,还是沿东西方向 量,还是朝民主街方向量,还是朝自由大道方向量....也就是度规还与方向有关。还有比这 更黑心变态的地头蛇吗?那种国度最后被上帝警告惩罚,地头蛇稍有收敛,将同一位置不同 方向的度规兑换率用一个简单函数约束。只要知道三个互相垂直方向的两两兑换率(对三维 流形总共是9个,对吧?)就可以知道任意方向的兑换率。这9个值就是度规张量。不同地方 的度规张量之间的转换(联络系数)也可以决定:度规-->联络-->曲率(后面细讲)。 这里我们也看到一个数学与物理、化学和生物的范式对应:线段、长方形和长方体就是数学 里的原子、分子和微晶,由此堆集出千千万万的流形(包括纤维丛)。 休息完,继续爬。
底流形上的转换函数之非平庸由结构群描述。例如,Mobius带,我们注意到平面与弯折纸带 可能有整体的差异。这是什么意思呢?从纸带上垂直于纸面放一根铅笔,当他沿纸带走一圈 回来时,平庸情形没有变化,但在扭曲带上走时会反向。的结构群为{1,-1},-1出现在反向 黏贴的那个地方。
类似地,纤维也有"转换函数"的对应物,由叫和乐群的东西描述。再看Mobius带。现在,不 同于平庸情形的"相邻直线或纤维完全等价",相邻"直线"满足特定的转换关系(这就是称为" 局部规范变换"的东西)。和乐群归根到底由结构群决定。
对于一个普通的黎曼流形而言,休息时提了,流形的度规张量完全决定联络系数。而对于一 个纤维丛而言,底流形的度规张量加上纤维的holonomy群才能决定联络。底流形上完成一个 循环时纤维空间可能没有回归原状,和乐群是指纤维变化的变换群。 细心的朋友可能会说,你讲的所谓整体差异还不是那些局部差异(规范变换)积累起来的吗? 铅笔指向在扭曲带上走一圈出现倒向还不是他在走的过程中慢慢逐步积累起来的? 太对了。把这句话将得更清楚一点,就是给一批大师赢来功名利禄的东西。包括陈大师省身 先生。即所谓的"将整体不变量用某些局部性质的积分表示"。别急,这个东西我们后面也要 把他弄得清清楚楚明明白白。
至此,看官自己就可以给纤维丛下定义了。需要的东西为:底空间,纤维空间,转换映像, 还有结构群,或简记为E(F,M,π,G)。看官看看时间,您花了多久到这里?数学系本科生四 年下来能到达这一步的,罕也,Princeton,Oxford不例外。
好,现在讲一讲切丛,他是最常见的也是最重要的纤维丛。过底空间上每一点可以画出无限 多条切线,构成切平面。因此可以将切平面当作纤维与底空间合成一个纤维丛,故名切丛。 每个切空间也是一个向量空间,故切丛也是向量丛。 于是,我们知道所谓纤维丛的截面就是每一根纤维上拿一点(一个值)来拼出来的东西。是 平面曲线y=f(x)的推广。
以二维球面为底空间的切丛上的一个截面就是该球面上的一个向量场。 古典微积分中导数是函数的变化除以自变量的变化,推广到纤维丛就是截面的变化(平行移 动)对底流形参数的变化,这就是联络(一般有多个分量)。直感上可以猜到,纤维丛的联 络由底流形和纤维二者共同决定。
阁下有一个天生的纤维丛。脑袋表面是底空间,上面长的头发就是纤维,转换函数依赖于阁 下梳头的风格,结构群为平庸(不是吗?)。梳梳头,你得到纤维丛一个不同的截面。 前已述,群本身也是一个空间,因而我们可以将结构群的群空间就当作纤维空间,这种特殊 的纤维丛叫主丛。既然主丛的纤维与结构群同一,只需标出底空间和结构群即可,故主丛记 为P(M,G)。一个抽象群的元素都可以通过一些具体动作(操作)表现出来,叫群表示。李 群,平移群,点群,等等天上神仙客都可以来个投胎下凡,即具体化。具体化就是选定群元 素作用的场所,即表示空间。神迹在地球上表现。地球就是神的表示空间。看官可以看到, "表示空间"是多么地误导。当初要是叫表演空间多好。既然表演空间也是空间,我们假如将 此表演空间当作纤维,也可以构成纤维丛,叫主丛诱导的伴侣丛,简称伴丛,记为PxVg,x指 直乘,Vg是结构群G的表演空间,他是一个向量空间,故伴丛也叫伴向量丛。
下面是插曲,看官尽管可以略过。
令人惊心动魄的是这些看似灵界仙境才有的东西刚好是我们描述自然界的最可靠工具。现在 物理学家认同所有的相互作用都是规范场刻画,而规范场在数学上与纤维丛完全是一回事。 吴大俊和杨振宁证明规范势是纤维丛(主丛)上的联络,而规范场强是纤维丛(主丛底空间) 的曲率。朗朗乾坤其实只是纤维丛世界之投影,像在我们世界扮演重要角色的电子似乎生活 在三维空间,但实际上他的波函数是生活在以三维空间为底的纤维丛中。量子粒子由波函数 描述,通常包含内部自由度。内部自由度对应的波函数可以当作纤维,底空间可以是普通的 三维欧氏世界,也可以是(能量算子的)某个参数空间。因此,按纤维丛术语,体系的波函 数就是丛截面。相位部分有动力学部分,几何部分和拓扑部分,其中后两种由和乐群描写。 微观体系的很多"古怪"行为全因于此,例如成键机制,超导,量子霍尔效应等等。 插曲完了。
到此,我们完成至少70%了。迷雾渐散,人心趋定。
作为中国知识分子声音的一个子集,海外中文论坛上总是一片吵骂声,包括新语丝读书论坛 上也有那么多缺乏起码教养的,连说话的basic manners都没有,一上来就是要干架,死活 就是要"讲赢",还有那么多志愿的政府宣传员和党工。凭我的第八感,可以看得到那些人血 液里流动的毒素和他们精神里的恶瘤。相比之下,短兄和湘女既是正直的热心人,兼具绅士 /淑女风度和义士精神。短兄湘女精神境界令人赞赏,心理健康值得敬佩。因此,谨以今天 这篇拙文献给短江和湘女。中土这面大鼓,除盛产狼孩这种bad解以外,也还有polik,短兄 和湘女这样的良解,这面鼓或许还有一点点可能性予以修补
闲论Atiyah-Singer指标定理(4)─先声─从Euler到Riemann-Roch与Gauss-Bonnet-Chern 学习要反覆,无规的反覆,易易难难,难难易易,易难难易.......今天来点轻松的。
从鼓音、听床联系到原子分子结构和光谱,从平直空间到非欧几何,从单一流形到纤维丛, 我们可以看到数学是统领科学和一般生活的最乾净、最经济的思维方式。但实际上,数学家 并不像我们通常想像的那样厉害。前面提到的那些看起来很怪异的数学概念,每一个都有漫 长的历史。数学书中每一句话都是历经无数人千锤百链共同努力的结果。 我们今天更要凸显一个事实:绝大多数数学概念都可以以形象为基础来理解,也就是说绝大 部分数学是符合直觉的。不靠推导,不靠计算,光凭思考,可以学到(至少可以理解)绝大 部分数学。
我们今天从AS定理的远祖开始来考察一下AS定理的世系演化。
平面三角形的内角和等于180度这一定理,不能算是AS定理最早的祖先,但算得是一个好的 祖先代表。
这个简单例子让我们看到了几何体上有代数,三对边夹角之和是个常数。因此,我们知道无 穷多个三角形之所以能归为一类,用边数为3或角数为3来判断都不够好,而是因为有一个共 同的不变量π。这个不变量是几何不变量。
三角形还有别的不变量吗?当然有。大家可以验算一下:边数-顶点数=0对所有三角形也成 立(不许笑!),而且与几何不变量π没有关系。 这个不变数对任意多边形(平面的或立体的)都成立:边数-顶点数=0。有一点点意思了吧。 敏感的同学可能马上看到这个不变数0是由于任意多边形都是一个闭合的东东。 更多一点意思的是,推广到无穷多边形也是成立的,特别是对圆周也成立,虽然边和顶点已 经难以看出来了。
于是我们发现这个不变数0原来是不仅是三角形的,也不仅是多边形的,也不仅是圆周的,而 是任意封闭曲线的性质。任意封闭曲线有一个不变数0。这就是封闭曲线的所谓拓扑不变量。 到这时,我们看不到这个0与边数或顶点数之类的关系,边、顶点、形状、长度、面积等几何 量此时都不是本质性的东西。这说明几何之外,还有更一般的不变数,就是拓扑。拓扑不变 量更有包容性,能够对更多的东西声明主权:xxxx自古以来就是我的领土。 任意封闭曲线有一个不变数对应,据说在古希腊就有人提到,但直到18世纪大数学家欧拉才 真正认真对付。欧拉推广了上述不变数。他首先发现任意多面体的表面,存在关系:面数- 边数+顶点数=2。仿照上述例子,可以轻易地推广到无穷多面体表面,推广到任意封闭体表 面,如球面。可见这个数2是所有二维封闭曲面的拓扑不变量,叫欧拉示性数。想想欧拉活 在18世纪末,这种今天小孩子都知道的关系也才200年左右的历史。因此,必定还存在一些 简单美丽的数学结果等待我们去发现。
欧拉解决封闭曲面的示性数以后,又进一步处理了带洞的曲面,他发现(你也可以轻易验证) ,带洞曲面的示性数等于无洞封闭曲面的示性数减去洞数。例如,篮球表面挖个洞以后,其 示性数就变成1,它拓扑等价于一个圆盘或一张纸。轮胎面,也叫环面,如自行车内胎,也可 以想像是一个实心多面体先从中间挖掉一块(也是多面体),再淘空剩下的环体而得,故有 两个洞,由此可得其示性数为0。
前面讲过,数学里的一个很重要的事就是分类,因为要统一,要抽象,就必须知道哪些是同 一类。数学上的分类与别的领域的分类之基本原则并无两样─就是以共性为基础。 看到欧拉示性数,自然会想,它能不能用来做某种分类呢?答案是: you bet!实际上,二维 曲面的分类仅靠欧拉示性数就够了。 任意封闭连通曲面必与下面之一同胚:(1)球面,(2)有限个环面连通和,(3)带交叉 帽(Mobius柄)球面。
交叉帽(cross-cap),可以想像为变肥的Mobius带,但在倒向处有交线。见图: 也就是说二维曲面就只有这几个球面,环面和交叉帽这几个基本类。它们就是二维封闭连通 曲面世界的全部"元素"。(三维曲面的"元素"数目由Thurston猜出,由Perelman证明,这是 另外的故事了)
高维曲面的欧拉示性数可以很直接了当地推得,而且结果堪称最美妙的数学方程序: 对n维闭多面体,欧拉示性数等于顶点数-边数+面数-3维体数+...
χ= [(-1)^{i}a_{i}],对i求和。
也就是说,欧拉示性数是各维子流形之数目之加/减。因此,也有人把欧拉示性数念成交错 和。
欧拉交错和之意义无论如何强调都不会过份:事实上已经发现至少有10种类似的交错和,如 Betti数,还有后面要讲的上同调等,而每一个这种交错和的发现都是数学史上的大事!每一 个这样的交错和都导致新的惊人发现!
我们这里来看一个从示性数引发新思想的小例子。
咋一看封闭线面的这类欧拉示性数,看官可能会觉得有些神秘。但稍微想一想,就可以看出 门道。对平面封闭曲线而言,你可能猜想这个0应该与曲线上的点绕一个中心点跑了一圈以后 回到基点有关。似乎是切线斜率将所有值扫瞄一次。更仔细的分析表明,那个0是曲联机对每 一点的曲率求和的结果。
后来更发现,这一思想可以推广到封闭曲面─即欧拉示性数是曲面上曲率对整个曲面积分。 什么是曲率?微积分里讲过曲线的曲率,就是二阶导数。(一阶导数是斜率,没有忘吧。) 推广到高维是直接了当的:经过曲面(体)上每一点可以画很多(无限多)条曲线,因此应 该有很多(无限多)个曲率,分别对应沿(无限多个)不同方向的曲线的弯曲程度。一个点 处有无限多个曲率值,你可能会觉得是个麻烦,但实际上这些曲率并不都是独立的。例如, 对于二维曲面上的点,曲率顶多有9个独立分量,也就是说,知道沿9个方向的曲率值,其他 任何方向的曲率可以推算出来。这9个值构成所谓的曲率张量。 欧拉示性数能表示成曲率对几何对象的积分。这是几何/拓扑近100多来的一个很热的主题, 可以说它直接催生了AS定理及其后裔。
欧拉示性数能给出流形的洞数描述,但洞可以有不同维度。系统记录各维洞的数目及分布, 有一个工具叫同伦群。从图像看很清楚。假如流形上有一些洞,如何标记它们呢?最简单的 方法就是把每个洞画个圈,表示"内为陷阱,禁止进入"。一维洞,用一维圈围住,二维洞, 得用二维洞才能围住,依此类推。总而言之,我们总可以用环绕每个洞的闭合流形将各维洞 包围起来。同伦群的最基本元素就是这样的包围圈。我们来看这些包围圈为何能形成群。事 实上对于每一个洞,我们可以用无限多个可能的包围圈将其包住,这些包围圈之间的差异只 是形状上的,它们都是等价的,叫同伦等价,因此同伦群元素是以类为"单位"的。同伦类形 成群的理由则简单得无法形容:对每个洞,我们不光可以包围一次,也可以包围任意多次, 可见包围n圈相当于是加法:围一圈,再围一圈,再围一圈...。而且我们容易注意到包围次 数不受次序的影响,因此同伦群是可交换的,即Abel的。更进一步,我们不光可以一次只围 一个洞,也可以一次围几个洞,形成不同的同伦类。看官想得出来,同伦类的数目决定了同 伦群的"自由元素"数目,也就是秩。由于不同维度的洞由不同维度的围道包围,故不同维 度的同伦群互相独立,也就是说,不同维度的同伦群(的元素)不会搅到一起。
作为一个例子,我们计算环面的同伦群。零阶同伦群为零,因为没有一维洞。一阶同伦群有 三个元素(三种不同的同伦类):环面上平庸围道(可以收缩成一点),它们不影响同伦群。 环面上的非平庸围道有两种:一种是围绕大环的,一种是围绕小环的。两种非平庸围道都服 从整数的加法而成群,是为Z群(整数群)。因此环面的一阶同伦群为:Z Z。环面的所有高 阶同伦群(大于等于2阶)均为平庸(仅含单位)。
看官不妨算一下中间挖掉两个小圆的三角板的一阶同伦群。
每本拓扑学书都有一大章讲同伦群,一般要花几十页篇幅。凭我的经验,学习效果都远远不 如我5到10分钟的解释。写成文字就是上面几行。很多学生学完拓扑学还是不知道算简单形 状的同伦群,就是因为教材上的那种写法是以最错乱的方式写的。 休息亭:基本群。它就是一阶同伦群。也就是以一维围道为同伦类构成的群。基本群之所以 重要,除它能描述二维洞以外,它与Poincare猜想之关连可能是最重要的原因。Poincare猜 想是說,与球面S^{n}同伦的 n 维拓扑流形一定同胚于 S^{n} 。对三维流形(Poincare猜 想原始版的流形),可以表成:如果一个三维流形的基本群与三维球面的一样,则这个三维 流形就是一个三维球面(拓扑等价或同胚)。很奇怪这个如此"地道的拓扑学"猜想最后竟然 不是用拓扑学方法证明的。
同伦群直观,又是Abel的,是流形分析的一个好工具,也有一些美丽的定理帮我们减少计算。 例如,Bott的一个伟大发现是,正交群的同伦群有周期性。这个我们后面还要比较仔细地讲。 但一般而言,流形的同伦群计算并没有一个可以依循的通用演算步骤,因而可能很复杂甚至 没办法算。像一般n维球面的同伦群问题还没有解决。因此,为了描述流形的组成,还需要别 的工具。
欧拉示性数催生的另一个伟大概念是同调群。现在同调已是一个容易导致混乱的词,因为有 十几种不一样的东东都打着同调这个旗号。当然从本质上讲,所有的同调有一些共性:就是 都对应一个叫同调群的Abel群。基本元素为链,闭链,边缘链(与之对偶的为上链,上闭链, 上边缘链)。实际情况中,我们一般通过上下文可以得知用的是哪种同调。 我们这里先讲讲最简单的同调群,后面再讲别的,AS定理至少涉及到四种同调,我们当然都 要解释。由欧拉示性数得知,一个一般的流形可以由一些简单的"元素"拼成:顶点,边, 面,体...不同维度的子流形。链的概念就是这些小流形的各种组合,如一些顶点加一些连 接线,一些面拼成的多面形。当拼出的流形封闭时,就叫闭链,如三角形的三条边,长方体 上表面的四条边,长方体的的六个面,都形成闭链。看官容易看出,流形的边缘是特殊的闭 链,例如三角形的三条边,圆盘的边缘,球体的表面...所以边缘链必为闭链,反之闭链不一 定是边缘链。
对于给定的流形,我们可以形式地用边缘算子来求得其边缘。例如,球体在边缘算子作用以 后成球面。边缘的边缘为零或边缘没有边缘的事实可以说成边缘算子作用在边缘链上为零。 因此当我们得到一些闭链时,为了将其中的边缘链区分出来,可以用边缘算子去作用它们, 剩下来的就是非边缘链。不断作用下去,就得到流形的分解。 因此仅相差边缘链的闭链可以当作是同一等价类,即同调类。也就是说,可以将闭链按边缘 链作为商得到的群来表示一个流形的分解。这就是同调群。 其实,同调有两种等价的说法,即所谓的上同调和(下)同调,前者是由低维往高维走,后 者是由高维往低维走。你知道,这种分法必然没有本质差异,因此可以不管它。 同调群的计算比同伦群来得可操作多了,在流形上人为画些边,面,得到闭链,即可依固定 程序算得同调群。实际上,由于我们知道,同调群闭链的差异其实也是在各维洞附近表现特 别,故由洞数以及洞之分布,可以帮助我们(猜)得到同调群。 作为本讲的结束,请看官留意欧拉示性数有一个非常优美的同调群语言表述: χ= [(-1)^{i}dim h_{i}],对i求和。
即欧拉示性数等于各阶同调群的维数(也就是Betti数)之交错和。再次以交错和来表达拓 扑不变量!
写到这里,我突然看到诗兴盎然的短江兄,于是也跟着诗兴发作,特贴出来与看官分享,并 请短江兄修改。
─────────────────
颂不变量(polik自由诗体)
啊,伟大的不变量!
你是思维的灯塔,
你是黑夜的星光。
有你就有共同点,
有你就有恒等式,
有你就有准绳和皈依。
你是法律,你是指南,
你是地图,你是基石。
啊,伟大的不变量!
你是科学的生命,
你是文明的灵魂。
────────────────
将不变量换成荆,周末可骗得美餐一顿。
不难理解,寻找不变量是数学(物理)的一个永恒主题。一方面是追求不变量,另一方面是 从完全不同的角度看待几何或拓扑。我们下面得分开成平行的两讲(4A)和(4B),然后才 回到正题(4C)。各节题目预告如下:
闲论Atiyah-Singer指标定理(4A)─先声─从Euler到Riemann-Roch与Gauss-Bonnet-Chern: 微分形式,(上)同调
闲论Atiyah-Singer指标定理(4B)─先声─从Euler到Riemann-Roch与Gauss-Bonnet-Chern: Morse理论
闲论Atiyah-Singer指标定理(4C)─先声─从Euler到Riemann-Roch与Gauss-Bonnet-Chern: RR定理及其推广
闲论Atiyah-Singer指标定理(4A)─先声─从Euler到Riemann-Roch与Gauss-Bonnet-Chern:
微分形式,de Rham(上)同调 上同调类有十几种,名字也混乱。数学家里变态的多,有些人喜欢迷雾好混水摸鱼,有些人 则专门制造迷雾。我在这里引带你们躲过那些害人的东西,直奔要点。我会在不久的将来另 文彻底清算数学上的各类同调理论。到时你会发现,同调湖里的浑水是多么的污浊,而又多 么不应该。
中学微积分知识告诉我们,对于一条曲线,一阶导数即切线代表倾斜程度,即斜率,二阶导 数代表弯曲程度,即曲率。推广到高维情形,依然成立,只是方向多了些,斜率需要多个独 立分量(=流形维度),而曲率就更多了,是一个张量。以二维曲面为例。每点的切线(无 限条)构成一个切平面,一个平面可由一个二维向量空间代表。又由于过每一点可以画无限 多条曲线,故曲率也很多(无限多),他们的大小满足从基点到一个椭球表面的距离,因此 可以用一个椭球面来描写二维曲面某一点的曲率,椭球的三个轴和椭球的方位总共对应6个独 立值,叫做曲率张量的6个分量:
d^2/dx^2,d^2/dxdy, d^2/dxdz,d^2/dy^2,d^2/dydz, d^2/dz^2.
高维情形依然有切平面,但曲率张量的分量要多一些。
曲率张量的每个分量是一个二阶导数。曲率张量还是反对称的,即交换指标出现一个负号。 这是要点。
因此干脆将曲率张量的每个分量带上相应的dx_idx_j,i,j=1,2,...n. 并且规定dx_idx_j = - dx_jdx_i,这当然与通常微分乘法不同,但体现交换反对称性质,叫外微分。这个看似 简单的记号改变,外微分是一个巨大的创新,对简化计算至关重要,更重要的是,它是20世 纪微分几何发展的一个主动力。现代微分几何都是用这套记号。很多人都不加"外"字了。这 是最紧要的,建议看官在这里反覆几次。 将二阶导数配上外微分,就得到了表达成外微分形式的曲率张量。 巧的是,如此定义微分,积分会得到巨大简化,高维积分与一维积分一样简便。 更巧的是这样定义的微分形式按乘法构成群,叫 (de Rham)上同调群。 外微分形式还有很多巧,暂先不谈。
我们知道,把张量分量当作一个矩阵(高维)的元素以后,张量就是矩阵。因此曲率张量就 是曲率矩阵。微分形式的曲率张量就是微分形式构成的矩阵。用矩阵时,我们希望矩阵行为 端正,例如不要奇异,即有反矩阵存在。否则我们就不理睬它。我们对待曲率矩阵也是如此, 都假定它是a good guy。这样我们就可以找他的特征值(即曲率张量的主分量)。我想,如
何求矩阵特征值就不用提了吧,归根到底就是解行列式而已:
|Ω-Iλ|=0
Ω是曲率矩阵,λ是特征值。与平常解矩阵特征值问题的唯一差异是,这里的特征值也是微 分形式。
我们知道任何一个行列式可以展开,曲率矩阵对应的特征行列式做展开以后,按特征值的幂 次表示出来:
1 + c_1 λ + c_2 λ^2+....=0 (第一个系数总可令其为1,why?)
其系数c_1,c_2就是第一陈式,第二陈式,....。他们分别是2i(1陈式是微分形式,而且是用来表示纤维丛的拓扑不变量的最佳形式,这样表示的拓扑不变量 就叫示性类,或特征类,即陈类。
陈式是闭微分形式,非常重要。代表d c_i =0, i=1,2,...表明局部"平"(流形)或"丛局部 =局部积"(丛),但其积分非零(整体拓扑非平庸流形/丛不等于流形简单乘积),即他们 不是恰当微分形式,c_i不能(在整个流形上)写成全微分形式df_i。 [微积分里讲过,闭形式是指:w = fdx + gdy 满足 df/dy = dg/dx,因此dw=0, 但w本身不 能写成某个形式的全微分dW,即f 不一定等于dW/dx,g也不一定等于dW/dy。] 与同伦群的元素为"类"一样,同调群的元素也为"类",即同调类。可以更清楚地写出明显形式: k维同调群 = k维闭链群/k维边缘链群。同调群的秩或维由群元素数目决定,也即自由群部 分的秩。同调群的扭分量是指交换群中的有限阶(非自由)元素。 微分形式组成的同调类叫de Rham上同调类,相应的群叫de Rham上同调群。同样,可以写出 de Rham上同调群的明显形式:
k维de Rham上同调群 = k维闭形式群/k维正合形式群 基础或基本(上同调)类就是n维体积元dx_1dx_2...dx_n,积分时往往要先将"被积函数" (微分形式)里提取出基本类来。
Todd类其实就是陈类的某种重组(也有人叫Todd类为陈类的余类)。所以并非新东西,也是 一些微分形式拼出来的。之所以特别引入Todd类,目的是他与所谓Betti数的关系更直接。 [第4节讲了,betti数就是流形同调群(非扭部分)的维数(秩),其几何意义为将连通流 形剖分时,最多可以切几次而不将其分成两片。有人直观但粗略地说,"bett数代表流形上 各维洞的数目",知道betti数可以算出洞数,但并不是指betti数就是洞数!例如,pretzel 的一维betti数为6而不是洞数3。]
在最一般的意义下微分算子的作用可以理解为在流形间建立映射,对切场产生前向映射,对 余切场(微分形式)产生拉回映射。与本题相关的是椭圆微分算子的作用在丛截面之间建立 映射,对余切场(微分形式)产生拉回映射。微分算子象征的陈类在积分时需要"乘以"Todd 类。
虽然de Rham上同调类是微分形式类,但多数人觉得它比很多别的(上)同调类反而来得直观 友好。其实,微分形式与边缘的关系通过Stokes定理而表现得淋漓尽致:
或 ,
用文字表达就是:对流形整体的积分可以化成对该流形边缘的积分,或更一般地,微分算子 是边缘算子的伴随算子。所以de Rham上同调类与闭链同调类实如形影相伴。Stokes定理对任 何维度都成立。这个公式不光美妙,更充满神秘。我相信任何初次接触这个公式的人与看到 爱因斯坦的质能关系一样,会感受自己心灵的震颤!
短江兄谈到中国人服暴力不崇理性,十分中肯。这其实是所有落后民族社群的共同不变量。 中国历史上产生了众多超级混混而受人膜拜,却从未能产生一个哪怕是玩具版的Stokes定理。 再随便看看任何表现理性和需要深度的地方,中国人就得鸭蛋。八卦易经、宫廷狗斗、中医 风水、算命相术,这些所谓中华文化的精髓就是蒙昧、荒诞及其滋生的暴力风格,所谓辉煌 的中国历史就是愚民反覆被极少数看穿这些精髓的魔头所利用然后很快被烹宰的历史。方舟 子老师批中医,据理据实,用心良苦,粪青叫痛早在预料之中,但还有那么多朝野"精英"人 物来抵制方老师,难怪中国人最多也不可能产生一个哪怕只是形似Stokes定理的作品。
No comments:
Post a Comment