相对论与黎曼几何-13-四维时空  精选
精选
|||
13. 四维时空
在科学史上,恐怕没有哪一个理论,像相对论这样引发了这么多的“佯谬”。除了双生子佯谬之外,还有滑梯佯谬、贝尔的飞船佯谬、转盘佯谬等等,以及它们的许许多多变种。这些佯谬的产生,根本原因是出于对同时性、时钟变慢、长度收缩、相对性原理、不同参考系的观察者、统一时空等等概念的思考和质疑。时间和空间到底是什么?正如公元四世纪哲学家圣·奥古斯丁对“时间”概念的名言:“Ifno one asks me, I know what it is. If I wish to explain it to him who asks, Ido not know.”我把它翻译成如下两句:“无人问时我知晓,欲求答案却茫然。”相对论是否部分地回答了这个问题?尽管众口难调,见仁见智,但相对论起码为我们提供了一种科学的思路和方法,使我们能从物理数学的理论上较为详细地诠释这些概念,何况还有上百年大量实验结果及天文观测数据的验证和支持呢。修正尚可,否定不易,起码不是诋毁谩骂之辈能做到的。
像双生子佯谬一样,尽管佯谬本身往往涉及到加速度参考系,但分析和理解这些佯谬并不一定需要广义相对论,许多相关的问题也并非一定要使用弯曲时空来解释。况且,正如我们在介绍黎曼几何时提到的,黎曼流形的每一个局部看起来都是一个欧氏空间。那么,对广义相对论研究的弯曲时空而言,它的每一个局部看起来便都是一个闵可夫斯基空间。闵可夫斯基4维时空的性质对广义相对论至关重要,是理解弯曲时空、分析黑洞等奇异现象的基础。因此,我们有必要在介绍爱因斯坦的引力场方程之前,首先多了解一些闵氏时空。
闵可夫斯基时空是欧氏空间的推广,仍然是平坦的。闵氏空间与欧式空间的区别,是在于度规张量的正定性。在黎曼流形上局部欧氏空间中定义的度规张量场gij,是对称正定的。如果将时间维加进去之后,度规张量便不能满足“正定”的条件了。将非正定的度规张量场包括在内的话,黎曼流形的概念被扩展为“伪黎曼流形”。比较幸运的是,之前我们所介绍的列维-奇维塔联络及相关的平行移动、测地线、曲率张量等等概念,都可以相应地推广到伪黎曼流形的情形。
度规张量是一个二阶张量,可以被理解为我们更为熟悉的方形“矩阵”。在矩阵中也有“对称正定”的概念。所谓对称矩阵,是指行和列对换后仍然是原来矩阵的那种矩阵。度规张量的对称性,是由它的定义决定的:
ds2 = gijdxidxj
实际上,任何矩阵都可以分解成一个对称矩阵和一个反对称矩阵之和。根据以上度规的定义可知,gij的反对称部分对ds2的贡献为0,所以,度规张量可以被认为是一个对称矩阵。
矩阵为“正定”的意思可以理解为这个矩阵的所有特征值都是“正”的。欧氏空间度规的正定性意味着实际空间中的距离(弧长)的平方是一个正实数ds2= dx2 + dy2 +dz2。因而,欧氏空间的度规是一个对称正定的d函数,
闵可夫斯基时空的度规仍然是对称的,但却不是正定的:dt2= dt2 - dx2 - dy2 - dz2,其度规记为h函数。上式中的t是时间,x、y、z是3个空间维坐标,而dt取代了弧长ds,被称为固有时。
细心的读者可能会问:时间间隔和空间距离的量纲是不一样的,怎么把它们的平方加减到一块儿去了呢?这儿也是使用了一个约定俗成的原则:将光速定义成了1。也就是说,四维时空的度规本来应该表示成如下形式:c2dt2 = c2dt2 -dx2 - dy2 - dz2,c=1的原则使公式看起来简洁明了,但我们务必随时记住这点。
比较欧氏空间和闵氏空间,将它们的度规d函数和h函数写成矩阵形式:

公式(2-13-2)中,第一维的本征值1对应于时间,其它本征值为-1的3个维度对应于3维空间。
时间和空间统一在4维时空中,是为了数学上的方便。爱因斯坦的狭义相对论揭示了时间空间的相对性及它们之间通过洛伦茨变换的互相关联。然而,时间和空间毕竟是不同的物理概念,时间用时钟来度量,空间用尺子来度量,将它们在4维时空中分别对应于本质不同的实数和虚数,这也反映了“时钟”和“米尺”不能互变的物理事实。
图2-13-1a的4维时空图实际上只画了3维,包括1个竖直方向的时间维和2个水平空间维。时间轴往上的方向表示未来,向下便代表过去。图中的圆锥被称为光锥。以时空中的一点为锥顶的光锥将这个点附近的时空分成类时、类光、类空三个部分。
四维时空中的一个点,有时间有地点,按照通常的意义把它叫做一个“事件”。例如,图2-13-1b中的A点,表示粒子初始时刻t1的空间坐标为(x1,y1)这个“事件”,后来,在时刻t2,粒子运动到了空间位置(x2,y2),即粒子最后在时空中的位置,这个“事件”用点B(t2,x2,y2)来表示。图中从A到B的曲线,叫做粒子的“世界线”。
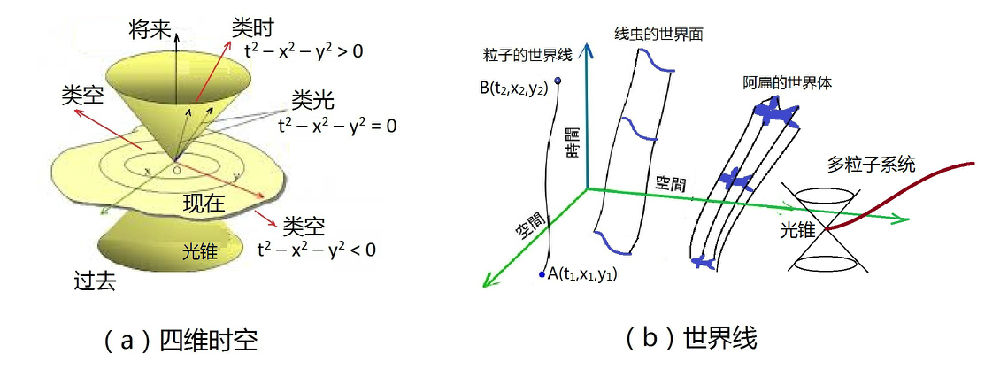
图2-13-1:四维时空和世界线
世界线,用以描述一个点粒子在时空中的运动轨迹。如果考虑的对象不是一个点,比如说,一条线虫,它在时空中的轨迹就成为了“事件面”,而要描述像阿扁那样的2维生物随时间长大的过程,就是个“世界体”了,见图2-13-1b。
在上一节中解读双生子佯谬时,将双生子的两次相遇当作2维时空中的两个事件点,然后,便可分别计算两条世界线的“固有时”再加以比较而得到答案。2维闵氏时空中两个任意事件之间直线路径的距离可表示为:
t2 = t2- x2
这个表达式右边的数值为正、零、负,分别定义了两个事件之间的相对关系:是类时、类光、还是类空。如果两事件的关系是类时的,t代表的才是固有时。类时关系说明两个事件之间可以有因果关联。比如双生子中的“刘天出生”(事件O),和“刘天返回地球”(事件D)这两个事件,一定是O在前,D在后,刘天不可能先返回地球再出生,无论从哪个参考系观察,这个结论都不会改变,这是“类时”的特点和物理意义。如果两个事件的关系是“类光”,t2 =0,说明它们互相位于另一个的光锥上,只有速度最快的光才能将它们联系起来。那么,类空(t2 <0)又是什么意思呢?在类空的情形下,两个事件之间的间隔无法叫做“固有时”了,因为它的本质已经不是时间,而更像空间。它可以被另一个物理量,即“固有距离”s来表征:s2= x2- t2。“类空”说明两个事件之间不可能具有因果关系,除非存在超光速的信号,才能将它们互相联系起来,但这是违反狭义相对论的基本假设的。所以,两个类空事件点之间不可能有真实粒子的“世界线”,真实粒子世界线的位置一定在光锥以内,是类时的。类空的两个事件互相位于对方的光锥之外。

图2-13-2:二维闵可夫斯基时空中事件之间的关系
如图2-13-2a中,很容易看出事件之间的关系:相对于事件O而言,事件B、G、F是类时的;事件E是类光的;事件A、C、D是类空的。图2-13-2b中的事件1和事件2互为类空,类空事件的时间顺序可以用坐标变换来改变。比如,从图2-13-2b中可见,事件1和事件2在Bob的坐标系(黑色)和Alice的坐标系(红色)中,发生的时间顺序不一样。在黑色(假设为静止)坐标系中的Bob看来,发生在t=0的事件1先于发生在t=1的事件2。红色坐标系相对于黑色作匀速直线运动,在其中的观测者Alice看起来,事件1仍然发生在t’=0处,但事件2却是发生在t’=-1的地方,发生时间早于事件1发生的时间。因而,这两个类空相关的事件不可能有因果关系。
现在,我们再来看看作匀速直线运动的粒子和作匀加速直线运动的粒子的世界线在2维时空中看起来是个什么样子?图2-13-2c画出了它们的曲线形状。
对于作匀速直线运动粒子的情况,我们早就打过交道,因为洛伦茨变换将静止的坐标系变换成相对运动的坐标系。比如说,图2-13-2b中红色坐标系的时间t’轴,实际上就是(t=0,x=0)的粒子,朝着x方向作匀速运动v的世界线。图c中的三条红线,则分别表示t=0时,位于x上不同位置的3个粒子的世界线。也就是说,匀速直线运动粒子的世界线和牛顿力学中将粒子的轨迹表示成时间的函数是一致的,是一条直线。
下面考虑运动粒子作匀加速直线运动的情况,根据牛顿力学中x方向的匀加速运动公式:x=(1/2)at2,应该是一条抛物线,但抛物线很快就跑到了光锥的外面,说明速度增加到超过了光速,这显然不满足狭义相对论光速极限的假设,见图2-13-2c。用相对论可以证明,2维闵氏时空中的匀加速运动粒子的世界线不是抛物线,而是无限靠近光锥的双曲线。“无限靠近光锥”,说明粒子的运动速度越来越大,无限地接近光速,但永远不等于光速。图c中的3条蓝色曲线,便分别对应于3个不同粒子的世界线。但是,读者对此可能又有疑问:不是说的是匀加速运动吗?匀加速运动的加速度应该为常数,如果速度永远不能超过光速的话,这“匀加速”又体现在哪儿呢?这点解释起来有点复杂,不过大家需要明白的是,相对论的关键思想是:观察同一个物理量,不同的参考系将得到不同的数值。这儿的“加速度不变”,是对于作匀加速运动的参考系中的观测者自己而言,是他们自已感觉到的加速度,所谓的“固有加速度”不变。当我们坐在加速运动的汽车上的时候,会感到反方向的惯性力,加速度越大,惯性力也越大,人也越会有不舒服的感觉。那条双曲线表示“匀加速”的意思就是说:沿着这条世界线运动的人将始终保持同样程度的不舒服感。
闵可夫斯基空间中的匀加速运动坐标系叫做伦德勒(Rindler)坐标。伦德勒坐标有许多有趣的性质,是使用平坦的闵氏空间来分析黑洞附近物理的一个强有力的工具,在伦德勒空间中存在类似于黑洞附近的“视界”之类的概念,甚至于还有与“霍金辐射”相类似的“安鲁效应”等量子物理相关的现象。首先弄明白伦德勒空间,对理解真正的黑洞物理有很大帮助,因此,我们将在下一节中介绍它。
有效质量
编辑
目录
定义编辑
负的有效质量说明晶格对电子作负功,即电子要供给晶格能量,而且电子供给晶格的能量大于外场对电子作功。 有效质量概括了半导体内部势场的作用,使得在解决半导体中电子在外力作用下的运动规律时,可以不涉及内部势场的作用。
有效质量编辑
公式表示编辑
Ft=MV′-MV0一般认为作用后的瞬间V′近似零故上述公式可简化为Ft=-MV0(公式中的负号表示F、V0反向)
IV称为有效质量.如果移动中不受阻力则所有质点将完全偏聚在表面.由于金属液体存在粘度于是第二相质点不可避免地受到移动阻力F
补充说明编辑
(1)因为在一般的载流子输运问题中,可以把晶体电子(或空穴)看成是具有动量P= ħk(k是晶体电子的准动量)和能量E = P2/ 2m* 的粒子(量子波包),即认为晶体电子是带有质量m*的自由粒子,m*就是晶体电子的有效质量。这就是所谓准经典近似,即把晶体电子看作为具有一定有效质量的经典粒子(能量与动量的平方成正比)。但是,终究有效质量是一个量子概念,所以有效质量不同于惯性质量,它反映了晶体周期性势场的作用(则可正可负,并可大于或小于惯性质量)。有效质量的大小与电子所处的状态k有关,也与能带结构有关(能带越宽,有效质量越小);并且有效质量只有在能带极值附近才有意义,在能带底附近取正值,在能带顶附近取负值。
(2)对于立方晶体,为了让电导率是一个标量,可引入所谓电导率有效质量;例如Si,导带电子的电导率有效质量mcn与导带底的横向有效质量mt*和纵向有效质量ml*的关系为mcn = 3ml*mt*/(2ml*+mt*),价带空穴的电导率有效质量mcp与重空穴有效质量mph*和轻空穴有效质量mpl*的关系为mcp = ( mph*3/2+ mpl*3/2 ) / ( mph*1/2 + mpl*1/2 ) ≈ mph*。
(3)此外,为了方便讨论导带底不在Brillouin区中心的半导体(如Si)中载流子的能态密度函数,还引入了所谓状态密度有效质量。这种半导体的导带底等能面是旋转椭球面,则其中电子的有效质量不是一个分量(有一个纵向有效质量ml*和两个横向有效质量mt*);这种非球形导带底的能态密度分布函数比较复杂,但是如果把电子有效质量代换为所谓态密度有效质量mdn* =(ml* mt* mt*)1/3,则可以认为它的能态密度分布函数与球形等能面的一样。
对于有s个等价导带底(能谷)的情况,电子的态密度有效质量应该更改为mdn* =(s2 ml* mt* mt*)1/3。对Si,s=6, mdn*=1.08m0,mdp*=0.59m0;对Ge,s=4,mdn*=0.56m0,mdp*=0.37m0,;对GaAs,等能面是球面,s=1,mdn* =m*。
No comments:
Post a Comment