 、
、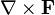 ,都可以用
,都可以用 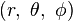 坐標表示,只要將標度因子代入在正交坐標系條目內對應的一般公式。
坐標表示,只要將標度因子代入在正交坐標系條目內對應的一般公式。球坐标系下的积分和微分公式[编辑]
假定 是從原點到 P 點的連線與正 z-軸的夾角
是從原點到 P 點的連線與正 z-軸的夾角- 线元素是一个从
 到
到  的无穷小位移,表示为公式:
的无穷小位移,表示为公式:
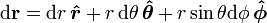 ;
;
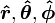 是在
是在 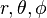 的各自的增加的方向上的单位矢量。
的各自的增加的方向上的单位矢量。- 面积元素1:在球面上,固定半径,天顶角从
 到
到  ,方位角从
,方位角从  到
到  变化,公式为:
变化,公式为:
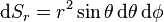 。
。
- 面积元素2:固定天顶角
 ,其他两个变量变化,則公式为:
,其他两个变量变化,則公式为:
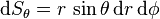 。
。
- 面积元素3:固定方位角
 ,其他两个变量变化,則公式为:
,其他两个变量变化,則公式为:
 。
。
- 体积元素,徑向坐標从
 到
到 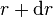 ,天顶角从
,天顶角从 到
到  ,并且方位角从
,并且方位角从  到
到  的公式为:
的公式为:
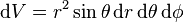 。
。
- 梯度公式:
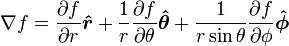 。
。
- 散度公式:
 。
。
- 旋度公式:
 。
。
 。
。
维基百科,自由的百科全书
在數學裏,一個正交坐標系定義為一組正交坐標 ,其坐標曲面都以直角相交。坐標曲面定義為坐標
,其坐標曲面都以直角相交。坐標曲面定義為坐標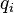 的等值曲面,或等值超曲面。例如,三維直角坐標
的等值曲面,或等值超曲面。例如,三維直角坐標 是一種正交坐標,它的
是一種正交坐標,它的 為常數,
為常數, 為常數,
為常數, 為常數的坐標曲面,都是互相以直角相交的平面,都互相垂直。
為常數的坐標曲面,都是互相以直角相交的平面,都互相垂直。
正交坐標時常用來解析一些出現於量子力學、流體動力學、電動力學、熱力學等等的偏微分方程。舉例而言,選擇一個恰當的的正交坐標來解析氫離子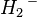 的波函數或消防水管的噴水,也許會比用直角坐標方便的多。這主要是因為恰當的正交坐標能夠與一個問題的對稱性相配合,從而促使應用分離變數法來成功的解析關於這問題的方程式。分離變數法是一種數學技巧,專門用來將一個複雜的
的波函數或消防水管的噴水,也許會比用直角坐標方便的多。這主要是因為恰當的正交坐標能夠與一個問題的對稱性相配合,從而促使應用分離變數法來成功的解析關於這問題的方程式。分離變數法是一種數學技巧,專門用來將一個複雜的 維問題變為
維問題變為 個一維問題。很多問題都可以簡化為拉普拉斯方程或亥姆霍茲方程,這些方程式可以用很多種正交坐標來分離。
個一維問題。很多問題都可以簡化為拉普拉斯方程或亥姆霍茲方程,這些方程式可以用很多種正交坐標來分離。
在數學裏,存在有各種各樣無限多的正交坐標系。應用二維直角坐標系 的共形映射方法,可以簡易的生成這些正交坐標系。一個複數
的共形映射方法,可以簡易的生成這些正交坐標系。一個複數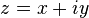 的任何全純函數
的任何全純函數 ,其複值的導數,如果不等於零,則會造成一個共形映射。如果答案可以表達為
,其複值的導數,如果不等於零,則會造成一個共形映射。如果答案可以表達為 ,則
,則 與
與 的等值曲線以直角相交,就好似原本的
的等值曲線以直角相交,就好似原本的 與
與 的等值曲線以直角相交
的等值曲線以直角相交
三維與更高維的正交坐標系可以由一個二維正交坐標系生成,只要將二維正交坐標往一個新的坐標軸投射(形成類似圓柱坐標系的坐標系),或者將二維正交坐標繞著其對稱軸旋轉。可是,也有一些三維正交坐標系,例如橢球坐標系,則不能夠用上述方法得到。
 ,可以寫為無窮小坐標位移的平方和:
,可以寫為無窮小坐標位移的平方和:
 是維數,標度因子
是維數,標度因子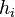 是度規張量的對角元素
是度規張量的對角元素 的平方根:
的平方根:
從前面的距離公式,可以觀察出,一個正交坐標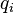 的無窮小改變
的無窮小改變 ,其相伴的長度是
,其相伴的長度是 。因此,一個位移向量的全微分
。因此,一個位移向量的全微分 等於
等於
 是垂直於
是垂直於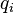 等值曲面的單位向量,指向著
等值曲面的單位向量,指向著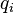 增值最快的方向,這些單位向量形成了一個局部直角坐標系的坐標軸。
增值最快的方向,這些單位向量形成了一個局部直角坐標系的坐標軸。
在正交坐標系裏,內積的公式仍舊不變:
 沿著周線
沿著周線 的線積分等於
的線積分等於
 是向量
是向量 在單位向量
在單位向量 方向的分量:
方向的分量:
 對於一個曲面
對於一個曲面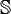 的曲面積分是
的曲面積分是
 ,其坐標曲面都以直角相交。坐標曲面定義為坐標
,其坐標曲面都以直角相交。坐標曲面定義為坐標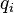 的等值曲面,或等值超曲面。例如,三維直角坐標
的等值曲面,或等值超曲面。例如,三維直角坐標 是一種正交坐標,它的
是一種正交坐標,它的 為常數,
為常數, 為常數,
為常數, 為常數的坐標曲面,都是互相以直角相交的平面,都互相垂直。
為常數的坐標曲面,都是互相以直角相交的平面,都互相垂直。正交坐標時常用來解析一些出現於量子力學、流體動力學、電動力學、熱力學等等的偏微分方程。舉例而言,選擇一個恰當的的正交坐標來解析氫離子
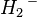 的波函數或消防水管的噴水,也許會比用直角坐標方便的多。這主要是因為恰當的正交坐標能夠與一個問題的對稱性相配合,從而促使應用分離變數法來成功的解析關於這問題的方程式。分離變數法是一種數學技巧,專門用來將一個複雜的
的波函數或消防水管的噴水,也許會比用直角坐標方便的多。這主要是因為恰當的正交坐標能夠與一個問題的對稱性相配合,從而促使應用分離變數法來成功的解析關於這問題的方程式。分離變數法是一種數學技巧,專門用來將一個複雜的 維問題變為
維問題變為 個一維問題。很多問題都可以簡化為拉普拉斯方程或亥姆霍茲方程,這些方程式可以用很多種正交坐標來分離。
個一維問題。很多問題都可以簡化為拉普拉斯方程或亥姆霍茲方程,這些方程式可以用很多種正交坐標來分離。在數學裏,存在有各種各樣無限多的正交坐標系。應用二維直角坐標系
 的共形映射方法,可以簡易的生成這些正交坐標系。一個複數
的共形映射方法,可以簡易的生成這些正交坐標系。一個複數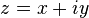 的任何全純函數
的任何全純函數 ,其複值的導數,如果不等於零,則會造成一個共形映射。如果答案可以表達為
,其複值的導數,如果不等於零,則會造成一個共形映射。如果答案可以表達為 ,則
,則 與
與 的等值曲線以直角相交,就好似原本的
的等值曲線以直角相交,就好似原本的 與
與 的等值曲線以直角相交
的等值曲線以直角相交三維與更高維的正交坐標系可以由一個二維正交坐標系生成,只要將二維正交坐標往一個新的坐標軸投射(形成類似圓柱坐標系的坐標系),或者將二維正交坐標繞著其對稱軸旋轉。可是,也有一些三維正交坐標系,例如橢球坐標系,則不能夠用上述方法得到。
向量與積分[编辑]
用數學術語,正交坐標的度規張量絕對沒有非對角項目。換句話說,無窮小距離的平方 ,可以寫為無窮小坐標位移的平方和:
,可以寫為無窮小坐標位移的平方和: ;
;
 是維數,標度因子
是維數,標度因子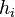 是度規張量的對角元素
是度規張量的對角元素 的平方根:
的平方根: 。
。
從前面的距離公式,可以觀察出,一個正交坐標
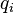 的無窮小改變
的無窮小改變 ,其相伴的長度是
,其相伴的長度是 。因此,一個位移向量的全微分
。因此,一個位移向量的全微分 等於
等於 ;
;
 是垂直於
是垂直於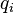 等值曲面的單位向量,指向著
等值曲面的單位向量,指向著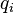 增值最快的方向,這些單位向量形成了一個局部直角坐標系的坐標軸。
增值最快的方向,這些單位向量形成了一個局部直角坐標系的坐標軸。在正交坐標系裏,內積的公式仍舊不變:
 。
。
 沿著周線
沿著周線 的線積分等於
的線積分等於 ;
;
 是向量
是向量 在單位向量
在單位向量 方向的分量:
方向的分量: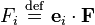 。
。
 ,
,
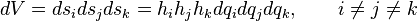 。
。
 對於一個曲面
對於一個曲面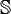 的曲面積分是
的曲面積分是 。
。
No comments:
Post a Comment