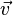 (in three dimensions) is a 9-term second-rank tensor (that is, a 3×3 matrix), but can be denoted simply as
(in three dimensions) is a 9-term second-rank tensor (that is, a 3×3 matrix), but can be denoted simply as 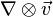 , where
, where  represents the dyadic product. This quantity is equivalent to the transpose of the Jacobian matrix of the vector field with respect to space.
represents the dyadic product. This quantity is equivalent to the transpose of the Jacobian matrix of the vector field with respect to space.Del
From Wikipedia, the free encyclopedia
No comments:
Post a Comment