[DOC]商空间
210.44.176.183/jpkc3/lxy/tpx/document/教案/3.3.doc
轉為繁體網頁
所谓商集乃是在一个集合中给定了一个等价关系之后将相对于这个等价关系而言的 ... 映射f: X→Y称为一个开映射(闭映射),如果对于X中的任何一个开集(闭集)U,象 ...
集合論(七):等價關係、等價類、商集
- 定義:設R為集合X上的一個二元關係,即R
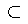 X×X。
X×X。 - 稱R為自反性如果對於X的任意元素x,有xRx。
- 稱R為反自反性如果對於X的任一個元素x,有
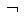 (xRx),即(x,x)
(xRx),即(x,x)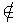 R。
R。 - 稱R為對稱性如果對於X的任意元素x、y,都有xRy → yRx。
- 稱R為反對稱性如果對於X的任意元素x、y,都有xRy
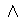 yRx →x=y。
yRx →x=y。 - 稱R為傳遞性如果對於X的任意元素x、y、z,都有xRy
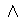 yRz →xRz。
yRz →xRz。 - 註:定義X×X的一個子集ΔX={ (x, x)
 X×X | x
X×X | x X },稱為X的對角線。
X },稱為X的對角線。 - R是自反的當且僅當ΔX
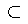 R。
R。 - R是對稱的當且僅當R=R-1,其中R-1是R的逆。
- 傳遞性的否定式:
- 例子:設Z為整數集合,固定一正整數n。在Z上定義一個關係:模n同餘的關係:
- 自反性:即證明:對所有的整數a,有(a, a)
 Rn。由於a-a=0=n的零倍,所以 (a , a)
Rn。由於a-a=0=n的零倍,所以 (a , a)  Rn。
Rn。 - 對稱性:要證明:對所有的整數a、b,有(a, b)
 Rn
Rn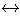 (b, a)
(b, a) Rn。
Rn。 - 傳遞性:要證明對所有的整數a、b、c,若 (a, b)
 Rn且(b, c)
Rn且(b, c) Rn 則(a, c)
Rn 則(a, c) Rn。由於(a, b)
Rn。由於(a, b) Rn且(b, c)
Rn且(b, c) Rn 所以a-b、b-c能被n整除。(注意:整除性與正負號無關。)因此由a-c =(a-b)+(b-c)及整除的性質,得知a-c也能被n整除。所以(a, c)
Rn 所以a-b、b-c能被n整除。(注意:整除性與正負號無關。)因此由a-c =(a-b)+(b-c)及整除的性質,得知a-c也能被n整除。所以(a, c) Rn 。
Rn 。 - 例子:
- X={a, b, c},R={ (a, b), (b,a), (a, c), (c, a)}。問R是否傳遞的?
- 例子:X={a, b, c},R={ (a, b), (b,a), (a, c), (c, a), (a, a), (b, b), (c,c)}。問R是否傳遞的?
- X={a, b, c},R=X×X。問R是否傳遞的?
- 定義:設R是在X上的一個等價關係。
- 設 a 為X的個元素,記[a]={ x
 X | aRx },稱[a]為a在R下的等價類(equivalence class) 或者陪集(coset )。它由所有與x有關的元素所組成。有以下刻劃: x
X | aRx },稱[a]為a在R下的等價類(equivalence class) 或者陪集(coset )。它由所有與x有關的元素所組成。有以下刻劃: x [a]
[a]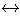 (a, x)
(a, x) R,即aRx。
R,即aRx。 - 由於aRa,所以a
 [a],即[a]≠
[a],即[a]≠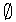 。任一個等價類[a]是X的一個非空子集,所以[a]是P(X)的一個元素。
。任一個等價類[a]是X的一個非空子集,所以[a]是P(X)的一個元素。 - 例子:
- 設X={ a, b, c }且R={ (a, a), (b, b), (c, c) }。
- 設X={ a, b, c }且R=X×X。試求X/R?
- 設Z為整數集,對於模n同餘關係Rn,試求Z/Rn有多少個等價類?
- 給出任一個整數b,可用歐氏算法將b=qn+r,其中q、r為整數,且r
 {0, 1, ... , n-1}共n個非負餘數。(雖然我們還未用集合論的方法來定義在整數集合上最常見的加減乘除,但這裡我們已接納了它們。其實直到現在連自然數也未有定義。)這個歐氏算法正如以前所學的短除法,只不過形式上改變了寫法。
{0, 1, ... , n-1}共n個非負餘數。(雖然我們還未用集合論的方法來定義在整數集合上最常見的加減乘除,但這裡我們已接納了它們。其實直到現在連自然數也未有定義。)這個歐氏算法正如以前所學的短除法,只不過形式上改變了寫法。 - 給出任一個整數b,若b=qn+r,此時差b-r=qn便能被n整除,因此(r, b)
 Rn,即b
Rn,即b [r]。明顯地,任何一個整數b,b會落在這n個等價類[0]、[1]、....、[n-2]、[n-1]之中的一個。
[r]。明顯地,任何一個整數b,b會落在這n個等價類[0]、[1]、....、[n-2]、[n-1]之中的一個。 - 現在要證明:這n個等價類兩兩不相等,且Z/Rn={[0]、[1]、....、[n-2]、[n-1]},共有n個等價類。
- 首先,[0]、[1]、....、[n-2]、[n-1]都是等價類,特別地,[i]
 Z/Rn。
Z/Rn。 - 由(ii)得知,Z/Rn
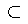 {[0]、[1]、....、[n-2]、[n-1]}。因此Z/Rn={[0]、[1]、....、[n-2]、[n-1]}。剩下來要證明{[0]、[1]、....、[n-2]、[n-1]}有n個兩兩不相的等價類。
{[0]、[1]、....、[n-2]、[n-1]}。因此Z/Rn={[0]、[1]、....、[n-2]、[n-1]}。剩下來要證明{[0]、[1]、....、[n-2]、[n-1]}有n個兩兩不相的等價類。 - 設i < j
 {0, 1, ... , n-1}為任意的,要證明等價類[i]、[j]兩兩不相同,只要證明:(i, j)
{0, 1, ... , n-1}為任意的,要證明等價類[i]、[j]兩兩不相同,只要證明:(i, j)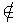 Rn(見下面的定理)。
Rn(見下面的定理)。 - 註:
- 如果X只有限多個元素,R是在X上的等價關係。則X/R只有有限多個等價類。而且每個等價類內的元素總數也是有限。
- 但有時即使X是無窮集合(即元素數見不是有限多個),有某些等價關係R使得商集X/R只有有限多個等價類。
- 引理一:
- (1)→ (2):假設aRb,要證明[a]∩[b]≠
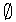 ,其實只需要證明[a]∩[b]包含元集b。
,其實只需要證明[a]∩[b]包含元集b。 - 由R的自反性,得知bRb,所以[b]必包含元素b。
- 此外由等價類的定義及aRb,得知[a]也包含b,因此[a]∩[b]包含元集b。
- (2)→(3):由於[a]∩[b]≠
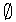 ,不妨假設集合[a]∩[b]包含x,要證明[a]=[b]。設c
,不妨假設集合[a]∩[b]包含x,要證明[a]=[b]。設c [a]∩[b],所以有aRc 及 bRc,由R的對稱性得知cRb,及從R的傳遞性有aRb。再由R的對稱性得知bRa。現證明[a]=[b]。
[a]∩[b],所以有aRc 及 bRc,由R的對稱性得知cRb,及從R的傳遞性有aRb。再由R的對稱性得知bRa。現證明[a]=[b]。 - 對於[a]的任一元素y,由等價類的定義得知aRy。又由bRa及R的傳遞性得知bRy。因此y也是[b]的一個元素。即[a]
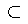 [b]。
[b]。 - 對於[b]的任一元素z,由等價類的定義得知bRz。又由aRb及R的傳遞性得知aRz。因此z也是[a]的一個元素。即[b]
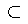 [a]。
[a]。 - (3) → (1):己知b
 [b]及[b]=[a],所以b
[b]及[b]=[a],所以b [a],跟據等價類[a]的定義,得aRb。
[a],跟據等價類[a]的定義,得aRb。
稱R為一個等價關係(equivalence relation)如果R滿足自反性、對稱性、傳遞性的條件。
設R是一個在X上的關係,則有
R是傳遞的當且僅當R。R
直接將關係的傳遞性改寫成形式語言:
R為傳遞性
R不滿足傳遞性
設a、b為整數,記
(a , b )
求證:Rn是整數集合Z上的等價關係:
假設(a, b)
由(a, b)
答:否定。因為(a, b)
答:否定。因為(b, a)
答:肯定。請給出理由。此外R是個等價關係。
將所有的等價類組成一個集合{[x]
求證:[a]={a}、[b]={b}、[c]={c}。此時 X在R下的商集X/R ={ {a}, {b}, {c} }。
答:由於 (a, c), (a, a), (a, b)
答:已證明Rn在Z上是個等價關係,分幾步進行探究商集Z/Rn:
因此{[0]、[1]、....、[n-2]、[n-1]}
證:(反證法)如果存在某兩個整數i、j滿足i < j
設R為X上的一個等價關係,[a]、[b]為X/R中的兩個等價類,則以下的三個條件是等價:
(1) aRb;
(2) [a]∩[b]≠
(3) [a]=[b]。
證:
No comments:
Post a Comment