练习题及答案
如图,有一弓形钢板ACB, 的度数为120°,弧长为l,现要用它剪出一个最大的圆形板料,则这一圆形板料的周长为( )。 的度数为120°,弧长为l,现要用它剪出一个最大的圆形板料,则这一圆形板料的周长为( )。 |
 |
题型:填空题难度:中档来源:同步题
所属题型:填空题 试题难度系数:中档
答案(找答案上“沪江中学题库”)
 |
考点梳理
初中一年级数学试题“如图,有一弓形钢板ACB,的度数为120°,弧长为l,现要用它剪出一”旨在考查同学们对 弧长的计算、 ……等知识点的掌握情况,关于数学的核心考点解析如下:
考点名称:弧长的计算
弧长的计算公式:

对圆形上任意一段弧的长度进行计算的公式。
定义:在圆周长上的任意一段弧的长度叫做弧长。有优弧劣弧之分。
弧长的计算:

弧长公式:弧长=θ*r,θ是弧度r是半径
l=nπr÷180或l=n/180·πr
在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=nπR÷180。
例:半径为1cm,45°的圆心角所对的弧长为
l=nπR÷180
=45×π×1÷180
约等于0.785(cm)
如果已知他的沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平,就得到圆锥的平面展开图。它是由一个半径为圆锥体的母线长,弧长等于圆锥体底面圆的周长的扇形和一个圆组成的,这个扇形又叫圆锥的侧面展开图。
补充公式:
S扇=nπR^2/360
=πRnR/360
=2πRn/360×1/2R
=πRn/180×1/2R
所以:S扇=RL/2
还可以是S扇=n/360πr²

对圆形上任意一段弧的长度进行计算的公式。
定义:在圆周长上的任意一段弧的长度叫做弧长。有优弧劣弧之分。
弧长的计算:

弧长公式:弧长=θ*r,θ是弧度r是半径
l=nπr÷180或l=n/180·πr
在半径是R的圆中,因为360°的圆心角所对的弧长就等于圆周长C=2πR,所以n°圆心角所对的弧长为l=nπR÷180。
例:半径为1cm,45°的圆心角所对的弧长为
l=nπR÷180
=45×π×1÷180
约等于0.785(cm)
如果已知他的沿圆锥体的一条母线和侧面与下底面圆的交线将圆锥体剪开铺平,就得到圆锥的平面展开图。它是由一个半径为圆锥体的母线长,弧长等于圆锥体底面圆的周长的扇形和一个圆组成的,这个扇形又叫圆锥的侧面展开图。
补充公式:
S扇=nπR^2/360
=πRnR/360
=2πRn/360×1/2R
=πRn/180×1/2R
所以:S扇=RL/2
还可以是S扇=n/360πr²
相关练习题推荐
与“如图,有一弓形钢板ACB,的度数为120°,弧长为l,现要用它剪出一”相关的知识点试题(更多试题练习--中学题库)
第二篇黎曼几何和广义相对论
1. 既古老又现代的几何学
几何是一门古老的学科。恐怕没有哪一门学科,像欧几里德几何学那样,在公元前就已经被创立成形,历经2000多年,至今还活跃在许多课堂上和数学竞赛试题中。尽管目前中国的中学教育已经不把平面几何当作必修课,一些学校删减了许多内容或者干脆取消了该门课程,但在上世纪的60-80年代,中国学生平面几何的水平肯定是算世界上比较高的。笔者还清楚地记得,解决平面几何难题,是本人中学时代的最爱。我们高中的数学老师兼班主任,是一个刚从师范毕业的年轻人,对数学教学充满热情。印象颇深的是他在黑板上画圆的绝活,他手握粉笔一挥一就,一笔下来,立刻在黑板上出现了一个规整的圆圈,用目测法很难看出这不是圆规画出来的。在他的影响下,我们班一半人都变成了数学迷,几何迷,大家在几何世界中遨游,从中体会到数学的奥妙,也感受到无限的乐趣。那两年,在教室的黑板上、课桌上,室外的石头边、树墩上,操场的篮球架上,随处可见同学们为思考几何题而画出来的三角形、直线、和圆圈。也许总体而言,中国式的教育方法忽略了发展学生改革创新的能力,但我深信,那个时代我们解决思考的无数道数学几何难题,对训练空间想象能力、逻辑推理能力,起了非常重要的作用。
纵观科学史,牛顿、爱因斯坦都是伟人,欧拉、高斯……伟大的数学家也可以列出不少,但恐怕很难找出像欧几里德这样的科学家,从2000多年前一直到现代,人们还经常提到以他命名的”欧几里德空间”、”欧几里德几何”等等名词,真可谓名垂千古而不朽了。阿基米德可能也能算一个,牛顿时代距离现在不过400来年,欧几里德和阿基米德却都是公元前古希腊时代的人物。
欧几里德的巨著—《几何原本》【1】(在1607年,有徐光启的中译本【2】),不仅仅被人誉为有史以来最成功的教科书,而且在几何学发展的历史中具有重要意义。其中所阐述的欧式几何是建立在五个公理之上的一套自洽而完整的逻辑理论,简单而容易理解。这点令人惊叹,它标志着在2000多年前,几何学就已经成为了一个有严密理论系统和科学方法的学科!
继欧几里德之后,16世纪法国哲学家、数学家笛卡儿(1596~1650年),将坐标的概念引入几何,建立了解析几何。
就平面几何而言,引入坐标的概念就是使用x、y来表示点、线、园等等图形在平面上的相对位置,因而便可以方便地应用解析的方法来处理几何的问题。如此一来,几何问题便成为代数的问题。这种处理方法使几何问题变得简单容易多了。说起来可笑,这种简单容易的方法反而使原来痴迷于求解平面几何难题的中学生们在刚学了解析几何之后,颇有一种失落感。因为解析几何使几何问题有了规范的解法,好像几何不再具有原来的魅力,原来那样有趣的几何学,被“解析”之后,突然间变得黯然失色、索然无味。
当然,谁也无法否认解析几何的诞生象征着几何发展的一个重要里程碑。解析几何不但能处理欧氏几何中的平面问题,还能解决三维空间的问题,以至于推广到更高维空间的几何问题。比如就说在二维和三维空间中吧,解析几何可研究的图形范围大大扩大。对平面曲线来说,欧氏几何中一般只能处理直线和圆。而现在有了坐标及函数的概念之后,直线可以用一次函数表示;圆可以用二次函数表示,二次函数不仅能够表示圆,还能表示椭圆、抛物线、双曲线等其它情形。除此之外,解析几何中还可以用一个任意的方程式f(x,y)=0,来表示所有的平面曲线,这些都使欧氏几何学望尘莫及。如果论及三维空间的话,在解析化之后,还能用三维坐标(x,y,z)和它们的代数方程式,表示各种各样的空间曲线和奇形怪状曲面。进一步谈到更高维的空间,欧几里德几何就更无用武之地了。
再到后来,数学的各个方面都有了巨大发展,特别是如我们在第一篇中所叙述的,牛顿和莱布尼茨发明了微积分,这是科学上的一件大事,使得那个时代的整个数学和物理都改变了面貌。那么,它对几何学的发展又有何种影响呢?
数学家们自然地将微积分这个强有力的工具用来研究几何学。实际上,微积分和几何的联系还更紧密一些,微积分的诞生也是得益于几何研究的,两者相互影响和发展。因此,微积分诞生之后不久,便有了“微分几何”这门新学科的萌芽。
法国数学家亚历克西斯·克莱洛(Alexis Clairaut ,1713 - 1763))是微分几何的先行者之一【3】。克莱洛是个名副其实的神童,他是母亲生下的20个子女中唯一一个长大成人的。在身为数学教授的父亲的严格管教和高标准要求下,克莱洛9岁开始读《几何原本》,13岁时就在法国科学院宣读他的数学论文。
之后几年,克莱洛迷上了空间曲线,他用曲线在两个垂直平面上的投影来研究空间曲线,第一次研究了空间曲线的曲率和挠率(当时被他称之为:双重曲率)。1729年,16岁的克莱洛将这个结果提交给法国科学院并以此申请法国科学院院士的资格,但当时未得到国王的立即认可。不过,只在两年之后,克莱洛发表了《关于双重曲率曲线的研究》一文,文中他公布了对空间曲线的研究成果,除了提出双重曲率之外,还认识到在一个垂直于曲线的切线的平面上可以有无数多条法线,同时给出了空间曲线的弧长公式,以及曲面的几个基本概念:长度、切线和双重曲率。这一年,18岁的克莱洛成为法国科学院有史以来最年轻的院士。
曲率和挠率是什么?我们先从平面曲线来认识曲率。

图2-1-1:克莱洛及双重曲率
我们首先需要引进曲线的切线,或称之为“切矢量”的概念,切矢量即为当曲线上两点无限接近时它们的连线的极限位置所决定的那个矢量。图2-1-1b中所标示的所有箭头,便是曲线的切矢量在曲线上各个点的直观图像。然后,再从图中切矢量沿着曲线的变化规律,又可以得到曲率的直观概念:曲率表征曲线的弯曲程度。比如说,图2-1-1b中最上面一条是直线,直线不会拐弯,其弯曲程度为0,即曲率等于0。这个0曲率与切矢量的变化是有关系的。看看直线上的箭头就容易明白了:上面所有箭头方向都是同样的。也就是说,曲率就是切矢量方向的变化率,或切矢量的旋转速率。直线上的切矢量方向不变,不旋转,对应于曲率为0。再看看图2-1-1b中下面两条曲线,当弧长增加时,切矢量不断旋转,曲线也随之而弯曲,切矢量旋转得越快,曲线的弯曲程度也越大。所以,曲率的几何意义就是曲线的切矢量对于弧长的旋转速度。
刚才在描述切矢量时,我们说它是“连线的极限位置所决定的那个矢量”,这儿我们很轻松地用上了“极限”的概念,诸位也毫不费力地就理解了它,因为大家学过了微积分。但是,在克莱洛的年代,曲率的计算可不是那么轻松容易的,这个十几岁的神童,天才地把微分的思想用于研究曲线,首次得到了这个结果。不仅如此,刚才我们讨论的只是平面曲线,克莱洛将微积分思想用于空间曲线。对一条平面曲线来说,如果每一点的曲率都确定了,这条曲线的形状便确定了。比如说,很容易直观地看出,一个圆上每个点的曲率都是一样的,等于它的半径的倒数。圆的半径越小,倒数则大,因而曲率便也越大;圆的半径越大,曲率则越小。因此,圆是等曲率的曲线,那么,现在我们考虑图2-1-2a中所示的平面螺旋线。因为平面螺旋线从内看到外,近似于一个一个从小到大的圆,所以,它的曲率是中心大边沿小。
我们可以将这个平面螺旋线想象成一个被压到一个平面上的的锥形弹簧,如果压力撤销之后,锥形弹簧恢复它的三维形状如图2-1-2b所示,这便得到了一条三维曲线。
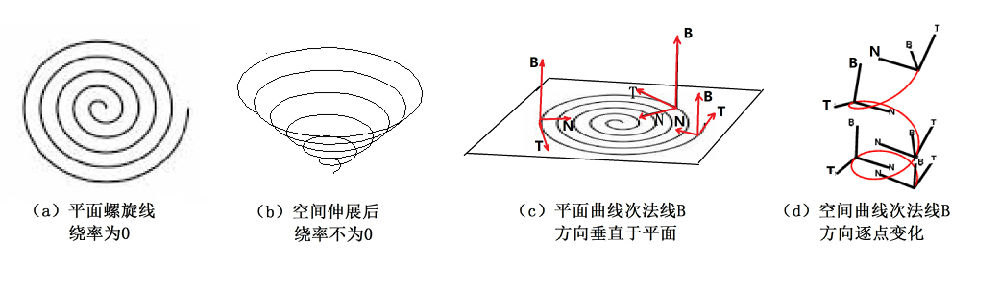
图2-1-2:空间曲线的挠率
首先让我们研究一下将平面螺旋线放在三维空间中的情形。如图2-1-2c所示,这时可以在曲线的每一个点定义一个由3个矢量组成的三维标架。令曲线的切线方向为T,在曲线所在的平面上有一个与T垂直的方向N。如果对于圆周来说,N的方向沿着半径指向圆心。N被称之为曲线在该点的主法线。为什么在法线的前面要加上一个“主”字呢,因为与切线T垂直的矢量不止一个,它们有无穷多个,都可以称为曲线在该点的法线,这些法线构成一个平面,叫做通过该点的法平面。刚才说过,这个事实是首先被小天才克莱洛认识到的。这所有的法线中,有一个是比较特别的,对平面曲线来说就是在此平面上的那一条法线,被称为主法线。有了切线T和主法线N,使用右手定则可以定义出三维空间中的另一个矢量B,B也是法线之一,称之为次法线。从图c很容易看出,螺旋线上每个点的切矢量T和主法线N的方向都逐点变化,唯有次法线B的方向不变。对一般的平面曲线也是如此,次法线的方向永远是垂直于曲线所在平面的,因此,一条平面曲线上每个点的次法线都指向同一个方向,即指向与该平面垂直的方向。
对一般的空间曲线,情况有所不同。想象一下让平面螺旋线中的每一圈逐渐从原来所在的平面慢慢被拉开,这时候,每一点次法线的方向便会从原来的垂直线逐渐发生偏离。也可以说,次法线的方向代表了与曲线“密切相贴”的那个平面,在一般三维曲线的情形下,这个密切相贴的平面逐点不一样,被称为曲线在这个点的“密切平面”。如图2-1-2d所示,对一般的三维曲线而言,在曲线上不同的点,三个标架T、N、B的方向都有所不同了。每一点的次法线B的方向也会变化,不过它仍然与该点的密切平面垂直。
克莱洛注意到空间曲线与平面曲线的不同,认为需要用另外一个曲率,后人称之为“挠率”的几何量来表征这种差别。换言之,挠率可以表示曲线偏离平面曲线的程度,被定义为次法线B随弧长变化的速率。
自组织与耗散结构
--摘自:方舟冲浪
自组织现象是指自然界中自发形成的宏观有序现象。在自然界中这种现象是大量存在的,理论研究较多的典型实例如:贝纳德(Bé nard)流体的对流花纹,贝洛索夫-扎鲍廷斯基(Belousov-Zhabotinsky)化学振荡花纹与化学波,激光器中的自激振荡等。自组织理论除耗散结构理论外,还包括协同学、超循环理论等,它们力图沟通物理学与生物学甚至社会科学,对时间本质问题等的研究有突破性进展,在相当程度上说明了生物及社会领域的有序现象。
耗散结构是自组织现象中的重要部分,它是在开放的远离平衡条件下,在与外界交换物质和能量的过程中,通过能量耗散和内部非线性动力学机制的作用,经过突变而形成并持久稳定的宏观有序结构。
耗散结构理论的创始人是伊里亚·普里戈金(Ilya Prigogine)教授,由于对非平衡热力学尤其是建立耗散结构理论方面的贡献,他荣获了1977年诺贝尔化学奖。普里戈金的早期工作在化学热力学领域,1945年得出了最小熵产生原理,此原理和翁萨格倒易关系一起为近平衡态线性区热力学奠定了理论基础。普里戈金以多年的努力,试图把最小熵产生原理延拓到远离平衡的非线性区去,但以失败告终,在研究了诸多远离平衡现象后,使他认识到系统在远离平衡态时,其热力学性质可能与平衡态、近平衡态有重大原则差别。以普里戈金为首的布鲁塞尔学派又经过多年的努力,终于建立起一种新的关于非平衡系统自组织的理论──耗散结构理论。这一理论于1969年由普里戈金在一次“理论物理学和生物学”的国际会议上正式提出。
耗散结构理论提出后,在自然科学和社会科学的很多领域如物理学、天文学、生物学、经济学、哲学等都产生了巨大影响。著名未来学家阿尔文·托夫勒在评价普里戈金的思想时,认为它可能代表了一次科学革命。
耗散结构理论可概括为:一个远离平衡态的非线性的开放系统(不管是物理的、化学的、生物的乃至社会的、经济的系统)通过不断地与外界交换物质和能量,在系统内部某个参量的变化达到一定的阈值时,通过涨落,系统可能发生突变即非平衡相变,由原来的混沌无序状态转变为一种在时间上、空间上或功能上的有序状态。这种在远离平衡的非线性区形成的新的稳定的宏观有序结构,由于需要不断与外界交换物质或能量才能维持,因此称之为“耗散结构”(dissipative structure)。[5]可见,要理解耗散结构理论,关键是弄清楚如下几个概念:远离平衡态、非线性、开放系统、涨落、突变。
(1)远离平衡态
远离平衡态是相对于平衡态和近平衡态而言的。平衡态是指系统各处可测的宏观物理性质均匀(从而系统内部没有宏观不可逆过程)的状态,它遵守热力学第一定律:dE=dQ-pdV,即系统内能的增量等于系统所吸收的热量减去系统对外所做的功;热力学第二定律:dS/dt>=0,即系统的自发运动总是向着熵增加的方向;和波尔兹曼有序性原理:pi=e-Ei/kT,即温度为T的系统中内能为Ei的子系统的比率为pi.
近平衡态是指系统处于离平衡态不远的线性区,它遵守昂萨格(Onsager)倒易关系和最小熵产生原理。前者可表述为:Lij=Lji,即只要和不可逆过程i相应的流Ji受到不可逆过程j的力Xj的影响,那么,流Ji也会通过相等的系数Lij受到力Xi的影响。后者意味着,当给定的边界条件阻止系统达到热力学平衡态(即零熵产生)时,系统就落入最小耗散(即最小熵产生)的态。
远离平衡态是指系统内可测的物理性质极不均匀的状态,这时其热力学行为与用最小熵产生原理所预言的行为相比,可能颇为不同,甚至实际上完全相反,正如耗散结构理论所指出的,系统走向一个高熵产生的、宏观上有序的状态。
(2)非线性
系统产生耗散结构的内部动力学机制,正是子系统间的非线性相互作用,在临界点处,非线性机制放大微涨落为巨涨落,使热力学分支失稳,在控制参数越过临界点时,非线性机制对涨落产生抑制作用,使系统稳定到新的耗散结构分支上。
(3)开放系统
热力学第二定律告诉我们,一个孤立系统的熵一定会随时间增大,熵达到极大值,系统达到最无序的平衡态,所以孤立系统绝不会出现耗散结构。那么开放系统为什么会出现本质上不同于孤立系统的行为呢?其实,在开放的条件下,系统的熵增量dS是由系统与外界的熵交换deS和系统内的熵产生diS两部分组成的,即:dS=deS+diS 热力学第二定律只要求系统内的熵产生非负,即diS>=0,然而外界给系统注入的熵deS可为正、零或负,这要根据系统与其外界的相互作用而定,在deS<0的情况下,只要这个负熵流足够强,它就除了抵消掉系统内部的熵产生diS外,还能使系统的总熵增量dS为负,总熵S减小,从而使系统进入相对有序的状态。所以对于开放系统来说,系统可以通过自发的对称破缺从无序进入有序的耗散结构状态。
(4)涨落
一个由大量子系统组成的系统,其可测的宏观量是众多子系统的统计平均效应的反映。但系统在每一时刻的实际测度并不都精确地处于这些平均值上,而是或多或少有些偏差,这些偏差就叫涨落,涨落是偶然的、杂乱无章的、随机的。
在正常情况下,由于热力学系统相对于其子系统来说非常大,这时涨落相对于平均值是很小的,即使偶尔有大的涨落也会立即耗散掉,系统总要回到平均值附近,这些涨落不会对宏观的实际测量产生影响,因而可以被忽略掉。然而,在临界点(即所谓阈值)附近,情况就大不相同了,这时涨落可能不自生自灭,而是被不稳定的系统放大,最后促使系统达到新的宏观态。
当在临界点处系统内部的长程关联作用产生相干运动时,反映系统动力学机制的非线性方程具有多重解的可能性,自然地提出了在不同结果之间进行选择的问题,在这里瞬间的涨落和扰动造成的偶然性将支配这种选择方式,所以普里戈金提出涨落导致有序的论断,它明确地说明了在非平衡系统具有了形成有序结构的宏观条件后,涨落对实现某种序所起的决定作用。
(5)突变
阈值即临界值对系统性质的变化有着根本的意义。在控制参数越过临界值时,原来的热力学分支失去了稳定性,同时产生了新的稳定的耗散结构分支,在这一过程中系统从热力学混沌状态转变为有序的耗散结构状态,其间微小的涨落起到了关键的作用。这种在临界点附近控制参数的微小改变导致系统状态明显的大幅度变化的现象,叫做突变。耗散结构的出现都是以这种临界点附近的突变方式实现的。
No comments:
Post a Comment