Saturday, February 20, 2016

Quantum superposition For an equation describing a physical phenomenon, the superposition principle states that a combination of solutions to a linear equation is also a solution of it.

Gauge fixing

From Wikipedia, the free encyclopedia
Jump to: navigation, search
Electromagnetism
Solenoid
Quantum field theory
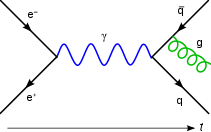
Feynmann Diagram Gluon Radiation.svg
Feynman diagram
History
In the physics of gauge theories, gauge fixing (also called choosing a gauge) denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field configurations. Any two detailed configurations in the same equivalence class are related by a gauge transformation, equivalent to a shear along unphysical axes in configuration space. Most of the quantitative physical predictions of a gauge theory can only be obtained under a coherent prescription for suppressing or ignoring these unphysical degrees of freedom.
Although the unphysical axes in the space of detailed configurations are a fundamental property of the physical model, there is no special set of directions "perpendicular" to them. Hence there is an enormous amount of freedom involved in taking a "cross section" representing each physical configuration by a particular detailed configuration (or even a weighted distribution of them). Judicious gauge fixing can simplify calculations immensely, but becomes progressively harder as the physical model becomes more realistic; its application to quantum field theory is fraught with complications related to renormalization, especially when the computation is continued to higher orders. Historically, the search for logically consistent and computationally tractable gauge fixing procedures, and efforts to demonstrate their equivalence in the face of a bewildering variety of technical difficulties, has been a major driver of mathematical physics from the late nineteenth century to the present.[citation needed]


Gauge freedom[edit]

The archetypical gauge theory is the Heaviside–Gibbs formulation of continuum electrodynamics in terms of an electromagnetic four-potential, which is presented here in space/time asymmetric Heaviside notation. The electric field E and magnetic field B of Maxwell's equations contain only "physical" degrees of freedom, in the sense that every mathematical degree of freedom in an electromagnetic field configuration has a separately measurable effect on the motions of test charges in the vicinity. These "field strength" variables can be expressed in terms of the electric scalar potential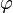 \varphi and the magnetic vector potential A through the relations:
{\mathbf E} = -\nabla\varphi - \frac{\partial{\mathbf A}}{\partial t}\,, \quad {\mathbf B} = \nabla\times{\mathbf A}.
If the transformation
\mathbf{A} \rightarrow \mathbf{A}+\nabla\psi




(1)
is made, then B remains unchanged, since
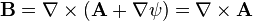{\mathbf B} = \nabla\times ({\mathbf A}+ \nabla \psi) = \nabla\times{\mathbf A}.
However, this transformation changes E according to
{\mathbf E} = -\nabla\varphi - \frac{\partial{\mathbf A}}{\partial t} - \nabla \frac{\partial{\psi}}{\partial t} = -\nabla \left( \varphi + \frac{\partial{\psi}}{\partial t}\right) - \frac{\partial{\mathbf A}}{\partial t}.
If another change
\varphi\rightarrow\varphi - \frac{\partial{\psi}}{\partial t}




(2)
is made then E also remains the same. Hence, the E and B fields are unchanged if one takes any function ψ(r, t) and simultaneously transforms A and φ via the transformations (1) and (2).
A particular choice of the scalar and vector potentials is a gauge (more precisely, gauge potential) and a scalar function ψ used to change the gauge is called a gauge function. The existence of arbitrary numbers of gauge functions ψ(r, t) corresponds to the U(1) gauge freedom of this theory. Gauge fixing can be done in many ways, some of which we exhibit below.
Although classical electromagnetism is now often spoken of as a gauge theory, it was not originally conceived in these terms. The motion of a classical point charge is affected only by the electric and magnetic field strengths at that point, and the potentials can be treated as a mere mathematical device for simplifying some proofs and calculations. Not until the advent of quantum field theory could it be said that the potentials themselves are part of the physical configuration of a system. The earliest consequence to be accurately predicted and experimentally verified was the Aharonov–Bohm effect, which has no classical counterpart. Nevertheless, gauge freedom is still true in these theories. For example, the Aharonov–Bohm effect depends on a line integral of A around a closed loop, and this integral is not changed by
\mathbf{A} \rightarrow \mathbf{A} + \nabla \psi\,.
Gauge fixing in non-abelian gauge theories, such as Yang–Mills theory and general relativity, is a rather more complicated topic; for details see Gribov ambiguity, Faddeev–Popov ghost, and frame bundle.

An illustration[edit]


Gauge fixing of a twisted cylinder. (Note: the line is on the surface of the cylinder, not inside it.)
By looking at a cylindrical rod can one tell whether it is twisted? If the rod is perfectly cylindrical, then the circular symmetry of the cross section makes it impossible to tell whether or not it is twisted. However, if there were a straight line drawn along the length of the rod, then one could easily say whether or not there is a twist by looking at the state of the line. Drawing a line is gauge fixing. Drawing the line spoils the gauge symmetry, i.e., the circular symmetry U(1) of the cross section at each point of the rod. The line is the equivalent of a gauge function; it need not be straight. Almost any line is a valid gauge fixing, i.e., there is a large gauge freedom. To tell whether the rod is twisted, you need to first know the gauge. Physical quantities, such as the energy of the torsion, do not depend on the gauge, i.e., are gauge invariant.


Quantum superposition

From Wikipedia, the free encyclopedia
Jump to: navigation, search
Quantum superposition of states and decoherence
Quantum mechanics
\sigma_x \sigma_p \ge \frac{\hbar}{2}
Quantum superposition is a fundamental principle of quantum mechanics. It states that much like waves in classical physics, any two (or more) quantum states can be added together ("superposed") and the result will be another valid quantum state; and conversely, that every quantum state can be represented as a sum of two or more other distinct states. Mathematically, it refers to a property of solutions to the Schrödinger equation; since the Schrödinger equation is linear, any linear combination of solutions will also be a solution.
An example of a physically observable manifestation of superposition is interference peaks from an electron wave in a double-slit experiment.
Another example is a quantum logical qubit state, as used in quantum information processing, which is a linear superposition of the "basis states" |0 \rangle and |1 \rangle . Here |0 \rangle is the Dirac notation for the quantum state that will always give the result 0 when converted to classical logic by a measurement. Likewise |1 \rangle is the state that will always convert to 1.


Theory[edit]

Examples[edit]

For an equation describing a physical phenomenon, the superposition principle states that a combination of solutions to a linear equation is also a solution of it. When this is true the equation is said to obey the superposition principle. Thus if state vectors f1, f2 and f3 each solve the linear equation on ψ, then ψ = c1 f1 + c2 f2 + c3 f3 would also be a solution, in which each c is a coefficient. The Schrödinger equation is linear, so quantum mechanics follows this.
For example, consider an electron with two possible configurations, up and down. This describes the physical system of a qubit.
c_1 \mid \uparrow \rangle + c_2 \mid \downarrow \rangle
is the most general state. But these coefficients dictate probabilities for the system to be in either configuration. The probability for a specified configuration is given by the square of the absolute value of the coefficient. So the probabilities should add up to 1. The electron is in one of those two states for sure.
p_\text{up} = \mid c_1 \mid^2
p_\text{down} = \mid c_2 \mid^2
p_\text{up or down} = p_\text{up} + p_\text{down} = 1
Continuing with this example: If a particle can be in state  up and  down, it can also be in a state where it is an amount 3i/5 in up and an amount 4/5 in down.
|\psi\rangle = {3\over 5} i |\uparrow\rangle + {4\over 5} |\downarrow\rangle.
In this, the probability for up is \left|\;\frac{3i}{5}\;\right|^2=\frac{9}{25}. The probability for down is \left|\;\frac{4}{5}\;\right|^2=\frac{16}{25}. Note that \frac{9}{25}+\frac{16}{25}=1.
In the description, only the relative size of the different components matter, and their angle to each other on the complex plane. This is usually stated by declaring that two states which are a multiple of one another are the same as far as the description of the situation is concerned. Either of these describe the same state for any nonzero \alpha
|\psi \rangle \approx \alpha |\psi \rangle
The fundamental law of quantum mechanics is that the evolution is linear, meaning that if state A turns into A′ and B turns into B′ after 10 seconds, then after 10 seconds the superposition \psi turns into a mixture of A′ and B′ with the same coefficients as A and B.



[PDF]Quantization of Gauge Theories
eduardo.physics.illinois.edu/...
University of Illinois at Urbana–Champaign
Loading...
Unlike systems which only have global symmetries, not all the classical configurations of vector potentials represent physically distinct states. It could be argued ...

Gauge fixing - Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Gauge_fixing
Wikipedia
Loading...
Any two detailed configurations in the same equivalence class are related by a gauge ... A particular choice of the scalar and vector potentials is a gauge (more .... not depend on the gauge function is said to be gauge invariant: all physical ... states, which are not observed in experiments at classical distance scales, one ...

Quantum superposition - Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Quantum_superposition
Wikipedia
Loading...
It states that much like waves in classical physics, any two (or more) quantum ... state can be represented as a sum of two or more other distinct states. ... For an equation describing a physical phenomenon, the superposition principle states that a ... Thus if state vectors f1, f2 and f3 each solve the linear equation on ψ, then ψ ...

Gauge theory - Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Gauge_theory
Wikipedia
Loading...
Its case is somewhat unique in that the gauge field is a tensor, the Lanczos tensor. ... 3.1 Classical electromagnetism; 3.2 An example: Scalar O(n) gauge theory .... orbit of mathematical configurations that represent a given physical situation to a ... to electromagnetism, we have a second potential, the vector potential A, with.

Euclidean Quantum Gravity - Page 131 - Google Books Result

https://books.google.com/books?isbn=9810205163
G. W. Gibbons, ‎Stephen W. Hawking - 1993 - ‎Science
This manipulation is not needed to construct Euclidean functional integrals ... the classical Euclidean actions of these theories are manifestly positive. ... given in a form in which not all field configurations are physically distinct. ... In electromagnetism, the physical fields are the transverse components of the vector potential Af; ...
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)