一個粒子在力場裡怎麼走,即彈來彈去的軌跡;古典力學討論其相對應的譜很小的時候,而量子力學即算子裡譜的問題,對應的譜很大的時候
| |
 1│2 1│2 
|
|
.丘成桐先生80年11月4日於中正大學應數所之演講,原載於數學傳播第十五卷第四期 |
| |
Laplacian
算子對應譜的最近發展
丘成桐先生演講
丘成桐
紀錄:賴玲淑;劉榮彰
|
|
| |
此篇文章主要是探討譜與區域的對應關係。首先介紹何謂 Laplacian 算子,所謂 Laplacian 算子在一維空間是定義為 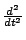 ,而在二維空間則定義為 ,而在二維空間則定義為 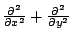 記做 記做
一開始,先看簡單的一維空間,通常在一維的 Laplacian 算子的譜的問題可由弦振動來解釋之,固定兩端點不動的均勻弦(密度 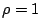 )。存在一組數列 )。存在一組數列 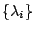 , ,
而由此
方程式,每任意特徵值 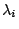 可對應一個特徵函數(基本波)ui,再將 ui 正規化,即 可對應一個特徵函數(基本波)ui,再將 ui 正規化,即 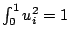 , , 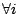 。 則對任意在[0, 1]
之間的函數(波)u,可用此基本波 ui 表示之。亦即 。 則對任意在[0, 1]
之間的函數(波)u,可用此基本波 ui 表示之。亦即
若此弦的密度 ρ 不均勻,那上述的方程要修正為
而在研究一維弦振動中有一重要性質,就是 Sturm-Liouville 性質:
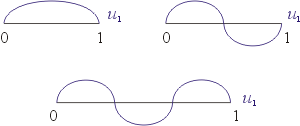
圖一 |
但此性質在二維空間以上就不存在了,所以在研究二維空間的問題比較困難,跟一維空間不同。
綜合上述,給定弦本身的密度 ρ,可以決定一組譜 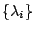 , , 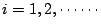 (其實 (其實 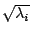 就是頻率)。反過來說,就是著名的 inverse 問題,即若給定 就是頻率)。反過來說,就是著名的 inverse 問題,即若給定 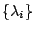 ,如何決定密度 ρ;相對的在二維空間也有 inverse 問題,即 Kac.Bochner 所提的問題 ,如何決定密度 ρ;相對的在二維空間也有 inverse 問題,即 Kac.Bochner 所提的問題
How to hear the shape of a drum?
那就是說,鼓可視為一個二維的有界區域
(domain),所謂鼓的形狀,就是相對於區域的幾何性質,這個問題就是怎麼樣從打鼓的音調聽出鼓的形狀。同樣的問題在一維空間的問題比較簡單,因為整個
potential 可以寫下來,二維空間以上就比較麻煩,我們考慮的方程式為
其中 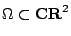 ,是一個有界區域。 ,是一個有界區域。
而 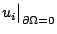 即對應於打鼓的時候,邊界不變。從此可提出許多問題,其中有個著名的問題:Ω 的幾何性與譜 即對應於打鼓的時候,邊界不變。從此可提出許多問題,其中有個著名的問題:Ω 的幾何性與譜 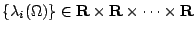 的對等性,其中已知 Ω 可決定譜 的對等性,其中已知 Ω 可決定譜 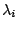 ,而 ,而 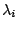 能否決定 Ω
將是主要探討的問題,在物理上而言,即是古典力學與量子力學的對應關係,那就是說一個粒子在力場裡怎麼走,即彈來彈去的軌跡;古典力學討論其相對應的譜很小的時候,而量子力學即算子裡譜的問題,對應的譜很大的時候 能否決定 Ω
將是主要探討的問題,在物理上而言,即是古典力學與量子力學的對應關係,那就是說一個粒子在力場裡怎麼走,即彈來彈去的軌跡;古典力學討論其相對應的譜很小的時候,而量子力學即算子裡譜的問題,對應的譜很大的時候
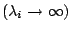 ,而這只是一個特別情形,實際上,在物理學裡,一般情況都有 potenial V(位能)存在,此時, ,而這只是一個特別情形,實際上,在物理學裡,一般情況都有 potenial V(位能)存在,此時,
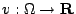 ,即考慮 ,即考慮
但此問題還未被完全瞭解,例如:
其中 M 是一個流形 (Manifold)
在此考慮 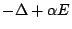 這算子,亦即 這算子,亦即
而加入 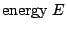 ,才會有好的譜分射。又一般在幾何上,都把 V 設定為
0,實際上,在微分幾何中並非不討論 ,才會有好的譜分射。又一般在幾何上,都把 V 設定為
0,實際上,在微分幾何中並非不討論 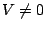 的情況,這要謹記在心。 的情況,這要謹記在心。
現在進入主要的問題: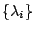 能否決定 Ω 的幾何性,對此問題可由二種不同的方法逼近,此二方法分別為
Wave mechanical approach 和 elliptic 問題。 能否決定 Ω 的幾何性,對此問題可由二種不同的方法逼近,此二方法分別為
Wave mechanical approach 和 elliptic 問題。
| (一)
Wave mechanical approach |
基本上 wave mechanical approach 可用 kernel mechanical 來看,即考慮 ![$\exp [it\sqrt{-\Delta}]$](http://episte.math.ntu.edu.tw/articles/mm/mm_15_4_01/img30.gif) ,其中 Δ 為 Laplacian 算子,從這邊其譜對應於 ,其中 Δ 為 Laplacian 算子,從這邊其譜對應於 ![$\exp [\sqrt{-1} t \sqrt{\lambda_i}]$](http://episte.math.ntu.edu.tw/articles/mm/mm_15_4_01/img31.gif) ,從此著手的好處是 Wave
equation(波動方程)可與古典力學聯結起來,因波動方程的傳播 (propagation) 速度是有限的 (finite),亦即在解波動方程時,如果在
t=0 時有 singularity,則在時間 t>0 時,singularity 仍存在,不會消失,這與連接算子的譜有很大關係,基本上研究的方法是考慮
kernel function(核函數) ,從此著手的好處是 Wave
equation(波動方程)可與古典力學聯結起來,因波動方程的傳播 (propagation) 速度是有限的 (finite),亦即在解波動方程時,如果在
t=0 時有 singularity,則在時間 t>0 時,singularity 仍存在,不會消失,這與連接算子的譜有很大關係,基本上研究的方法是考慮
kernel function(核函數)
的形式,這可解出 wave equation,且滿足 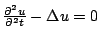 。但實際上, 。但實際上, 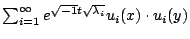 並不收歛,因而可發現其 singular
support 與 並不收歛,因而可發現其 singular
support 與 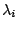 有關,然後由剛才寫下來的 w(x,y) 跟用不同的方法如微分幾何或其他方程方法計算方程的
approximate kenel,而後我們發現與 geodesic
flow(沿直線如何走的問題)有關,如此用這二種不同的方法得到的基本解,令它們相等,就可得到許多訊息 (information) 去探討 Ω,在物理上稱為
WKB method,同樣的方式亦可應用 ellitpic 方法,在下節將再做詳細說明。 有關,然後由剛才寫下來的 w(x,y) 跟用不同的方法如微分幾何或其他方程方法計算方程的
approximate kenel,而後我們發現與 geodesic
flow(沿直線如何走的問題)有關,如此用這二種不同的方法得到的基本解,令它們相等,就可得到許多訊息 (information) 去探討 Ω,在物理上稱為
WKB method,同樣的方式亦可應用 ellitpic 方法,在下節將再做詳細說明。
|
|
對外搜尋關鍵字:
.Laplacian算子 |
|
 |
|
| |
(若有指正、疑問……,可以在此 留言 或 寫信
給我們。) |
 |
EpisteMath (c) 2000
中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有
|
編輯:廖俊旻 ∕ 校對:黃怡碧
∕ 繪圖:簡立欣
| |
Laplacian 算子對應譜的最近發展
丘成桐先生演講 (第 2 頁)
丘成桐
紀錄:賴玲淑;劉榮彰
|
|
.丘成桐先生80年11月4日於中正大學應數所之演講,原載於數學傳播第十五卷第四期
‧對外搜尋關鍵字 |
| |
| (二)
elliptic 問題:即 Heat equation method |
首先考慮 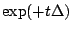 算子,並考慮 算子,並考慮 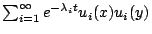 ,我們可以證明在 t>0 時會收歛。定義 ,我們可以證明在 t>0 時會收歛。定義 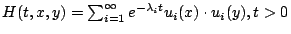 ,可知 H 不但收歛而且是 ,可知 H 不但收歛而且是 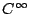 函數,此時
H(t,x,y) 滿足 函數,此時
H(t,x,y) 滿足
且
由此可知譜 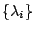 與函數 與函數 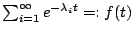 是等價的,從這個等價的結果,我們就發現一個方法來研究 是等價的,從這個等價的結果,我們就發現一個方法來研究 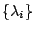 與古典力學的一些關聯性,這兩者的關係是什麼呢?就是說所謂 Heat equation,(*)可以用不同的方法來解,亦即可以用
approximate 方法來算,我們可以硬將其解寫下來。我們令 與古典力學的一些關聯性,這兩者的關係是什麼呢?就是說所謂 Heat equation,(*)可以用不同的方法來解,亦即可以用
approximate 方法來算,我們可以硬將其解寫下來。我們令
這就是在 n 維空間裡 Heat equation 的解(對應於所謂的
Gaussian
Distribution)。而現在我們在二維空間裡,熱方程式的解已經找到了!但我們需要加入一些邊界值的條件,(這有如我們固定一個區域,然後考慮熱從此區域流失的現象),亦即(*)變為
此時(**)的解就須加入一些項:
亦即 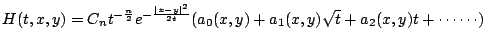 然後逐項的去解 ai, i=0,1,2,…,ai 可以用區域的幾何(如邊界的長度,曲率以及其微分, 然後逐項的去解 ai, i=0,1,2,…,ai 可以用區域的幾何(如邊界的長度,曲率以及其微分, )來表示。其實這樣解出來的無窮級數並不收歛,但這沒有造成什麼問題,因為我們只考慮當 t 很小的時候(這對於 )來表示。其實這樣解出來的無窮級數並不收歛,但這沒有造成什麼問題,因為我們只考慮當 t 很小的時候(這對於 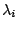 很大的時候);我們得到
很大的時候);我們得到
由(1)(2),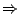
我們可證明 a0(x,x)=1,所以得到
亦即給定一組 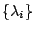 ,我們可以決定出 ,我們可以決定出
事實上,也可算出
其中 R 是曲率 (curvature)。
以上的 Heat equation method 也是用二種不同的方法,得到 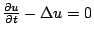 的基本解在 的基本解在 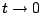 時,然後讓它們相等,得到一串訊息,如
時,然後讓它們相等,得到一串訊息,如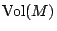 , , 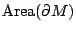 , ,  ,這是在eigenvalue(譜)中很重要的方法,可是此方法還是不夠用的,因為只看 ,這是在eigenvalue(譜)中很重要的方法,可是此方法還是不夠用的,因為只看 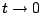 ,就像在 WKB method 中也會遺失了一些訊息,因此,也無法從 wave mechanical approach 和
elliptic 完全決定區域 Ω。 ,就像在 WKB method 中也會遺失了一些訊息,因此,也無法從 wave mechanical approach 和
elliptic 完全決定區域 Ω。
例: 在 wave equation 時,考慮 wave kernel,其訊息基本上是沿著
(travel along) characteristics 傳播,即所謂 null curve,在區域裡,相當於 geodesic,而從 geodesic
可以得到一串 eigenvalue 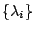 ,如何得到呢?我們在流形上說明比較容易。例如在
torus 上,有一個封閉的 geodesic,如下圖 ,如何得到呢?我們在流形上說明比較容易。例如在
torus 上,有一個封閉的 geodesic,如下圖
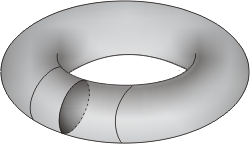
圖二 |
我們可以作一管狀鄰域 (tubelar neithborhood) V,然後可以得到一組函數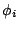 ;這些函數在 V 之外為 0(零),然後在這些 geodesics 附近有值,事實上 closed geodesic
本身就有許多訊息,我們可以定義 Poincaré map(映射),從這個映射,我們可以建構一組近似的 eigenfunction ;這些函數在 V 之外為 0(零),然後在這些 geodesics 附近有值,事實上 closed geodesic
本身就有許多訊息,我們可以定義 Poincaré map(映射),從這個映射,我們可以建構一組近似的 eigenfunction 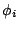 出來,即 出來,即 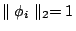 , , 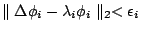 ,其中 ,其中 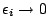 as as 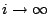 , , 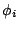 可以用 Poincaré map 寫下來,而對於這些
eigenvalues 的行為,我們知道的不多,但這一串的 eigenvlues 是無法從以上的方法 (Heat equation) 得到的。 可以用 Poincaré map 寫下來,而對於這些
eigenvalues 的行為,我們知道的不多,但這一串的 eigenvlues 是無法從以上的方法 (Heat equation) 得到的。
例如:torus 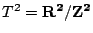 其 metric 為 dx2+dy2,曲率K=0,而在 T2
上,Heat equation 的近似解為 其 metric 為 dx2+dy2,曲率K=0,而在 T2
上,Heat equation 的近似解為 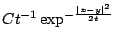 as as 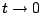 。亦即 。亦即
沒有了 lower terms,即只有 a0=1,其它都為
0,所以無法得到很好的訊息當 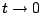 。但從 wave equation 可以找到所有的
closed geodesic 的長度,叫做 。但從 wave equation 可以找到所有的
closed geodesic 的長度,叫做 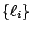 ,而 ,而 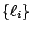 可由 可由 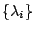 決定,又在某些特別情形下, 決定,又在某些特別情形下,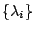 亦可由 亦可由 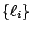 決定,至少在 tori 的情形可以決定 決定,至少在 tori 的情形可以決定
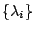 。如在 Mn(M 是
n 維流形),K=-1
時,我們可以證明 。如在 Mn(M 是
n 維流形),K=-1
時,我們可以證明 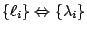 ,這即為著名的 Selberg trace formula。 ,這即為著名的 Selberg trace formula。
現在要講幾個做了很多年的問題,其中一個就是如何了解多少個 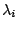 即決定 Ω 的幾何性質的問題,譬如 即決定 Ω 的幾何性質的問題,譬如 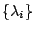 可決定 可決定 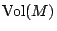 這個不變量,亦即從頻率決定了面積有多大(討論二維時),這就是前面所寫的公式:
這個不變量,亦即從頻率決定了面積有多大(討論二維時),這就是前面所寫的公式:
底下我們想想看事實上能否真正地決定面積的這個問題。考慮打一個鼓,是否可以聽出它的面積 (Area)
有多大?其實這是有點欺騙。因為打鼓的時候,只能聽到有限 (finite) 的 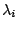 ,不可能將函數 ,不可能將函數
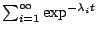 找出來。這邊一個問題就是這樣: 找出來。這邊一個問題就是這樣: 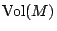 是否可以有效的決定 (determine effectively)?就是能不能真的從有限的 是否可以有效的決定 (determine effectively)?就是能不能真的從有限的 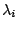 有效決定 有效決定 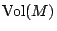 的問題,這個問題有可能沒辦法做到的。 的問題,這個問題有可能沒辦法做到的。

圖三 |
現在舉個最簡單的例子,就是考慮一個長方形區域(如上圖),慢慢拉長的時候,此時長方形的譜從兩邊得到,一邊從 x 方面,另一邊從 y 方向,而 x 方向有 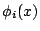
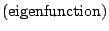 , y
方向有 , y
方向有 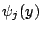 (eigenfunction),而 (eigenfunction),而 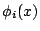 的相對固有值(eigenvalue) 為
的相對固有值(eigenvalue) 為 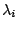 , ,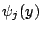 相對的固有值為 相對的固有值為
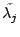 ,所以整個長方形的譜為 ,所以整個長方形的譜為 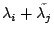 ,那現在有什麼問題呢?就是若此長方形拉的很扁(窄),即固定寬度(y 方向),長度拉長(x 方向),此時 ,那現在有什麼問題呢?就是若此長方形拉的很扁(窄),即固定寬度(y 方向),長度拉長(x 方向),此時
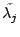 這邊很大, 這邊很大,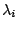 很小。而假如 很小。而假如
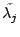 很大,就看不到 很大,就看不到 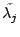 此時長方形的譜慢慢靠近 此時長方形的譜慢慢靠近 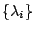 ,就有限步驟來看的時候,只看到 ,就有限步驟來看的時候,只看到 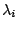 的部分,看不到 的部分,看不到 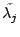 的部分( 的部分(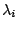 與 與 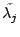 相較之下),所以從 相較之下),所以從 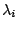 這邊看過去的話,無從曉得面積到底有多大?(因只有長度無法決定面積)。所以必須改變這問題,了解有效決定的意思。而不能說:
Given 這邊看過去的話,無從曉得面積到底有多大?(因只有長度無法決定面積)。所以必須改變這問題,了解有效決定的意思。而不能說:
Given 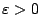 , determine Vol(M) up to ε 的問題為 , determine Vol(M) up to ε 的問題為 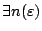 , , 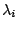 , , , ,
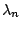 s.t. s.t. 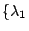 , ,  , , 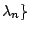 determine Vol(M) up to ε。剛才的例子就說明了不可能做到。所以,我們要想個辦法知它的意思,這個辦法就是給定 determine Vol(M) up to ε。剛才的例子就說明了不可能做到。所以,我們要想個辦法知它的意思,這個辦法就是給定
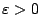 ,已知 ,已知 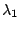 ,存在 ,存在 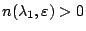 使得 使得 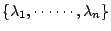 決定的誤差在 ε 之內。目前已知在 Ω 是凸區域 (convax) 時,能有效地決定 決定的誤差在 ε 之內。目前已知在 Ω 是凸區域 (convax) 時,能有效地決定 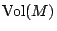 ,即 ,即
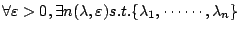 determine vol 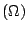 up to ε。
在此提出兩個 open question:
-
- Question 1. Area
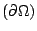 是否可被有限 是否可被有限 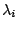 決定,當 Ω 是凸區域。亦即 Area 決定,當 Ω 是凸區域。亦即 Area
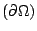 是否可用上述同樣的方法所決定? 是否可用上述同樣的方法所決定?
-
- Question 2. 若 Ω 不是凸區域(如 star-shape 星形區域)
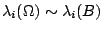 是否也可被有限 是否也可被有限 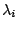 決定? 決定?
最後提二個類似的結果,一個著名的定理是:
則可推得Ω=Ball。
最近 Melas 得到下列有趣的定理:
-
-
- Melas: 若
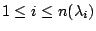 , , 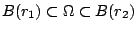 且 Ω 為 convax,則可得到 且 Ω 為 convax,則可得到 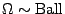 ,亦即存在半徑 r1,
r2 >0,使得 ,亦即存在半徑 r1,
r2 >0,使得 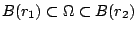 且 且 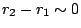 。 。
當把 Ω 為凸集的假設去掉,則 Melas 的結果能否成立呢?這是一個有趣的工作。
|
|
|
|
 |
|
| |
(若有指正、疑問……,可以在此 留言 或 寫信
給我們。) |
 |
EpisteMath (c) 2000
中央研究院數學所、台大數學系
各網頁文章內容之著作權為原著作人所有
|
| 編輯:廖俊旻 ∕ 校對:黃怡碧
∕ 繪圖:簡立欣 |
最後修改日期:4/26/2002 |
|
最後修改日期:4/26/2002 |
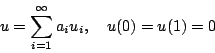
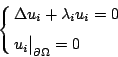
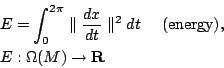
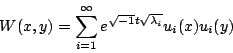

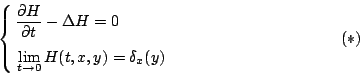
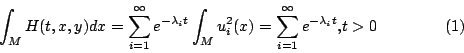
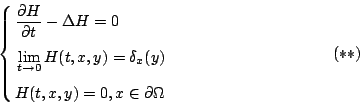
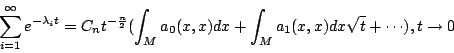
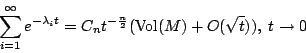
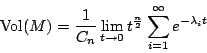
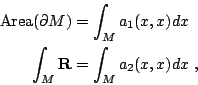

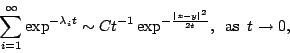
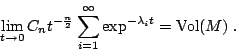

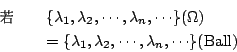
No comments:
Post a Comment