QMD模型初始化中的几个问题[量子分子动力学之家]
www.imqmd.com › 研究领域頁庫存檔 - 轉為繁體網頁
您公開 +1 了這個項目。 復原
2010年10月9日 – 1)初始核的动量分布是满足Fermi-Dirac分布的,这个主要是初始核子的动量由费米
气体模型给,费米气体理论本身就是要满足Fermi-Dirac分布的(看 ... 英語語言詞典[fermi momentum] # 翻譯[fermi momentum]
zh-tw.w3dictionary.org/index.php?q=fermi+momentum頁庫存檔Fermi momentum. 費米動量. zh-tw • #883519 • lan5ec-dictionary ... 費米動量. Fermi momentum. zh-tw • #667292 • lan5ce-dictionary ...費米能- 維基百科,自由的百科全書
zh.wikipedia.org/zh-hk/費米能頁庫存檔這個概念通常應用在能量和動量之間的色散關係上,與動量的方向無關。更一般的情況下,費米能更具有普遍意義。 費米速度指絕對零度下電子繞原子核運動的平均 ...
费米能- 维基百科,自由的百科全书
为电子质量。 这个概念通常应用在能量和动量之间的色散关系上,与动量的方向无关。更一般的情况下,费米能更具有普遍意义。 费米速度指绝对零度下电子绕原子核 ...
就一个由费米子组成的微观体系而言,每个费米子都处在各自的量子能态上。现在假想 把所有的费米子 从这些量子态上移开。之后再把这些费米子按照一定的规则(例如泡利原理等)填充在各个可供占据的量子能态上,并且这种填充过程中每个费米子都占据 最低的可供占据的量子态。最后一个费米子占据着的量子态 即可粗略理解为费米能级
- 有15篇回复贴
肖特基势垒是指具有整流特性的金属-半导体接触,就如同二极管具有整流特性。是金属-半导体边界上形成的具有整流作用的区域。
金属与n型半导体形成的肖特基势垒如图1所示。金属—半导体作为一个整体在热平衡时有同样费米能级。肖特基势垒相较于PN接面最大的区别在于具有较低的接面电压,以及在金属端具有相当薄的(几乎不存在)空乏区宽度。由半导体到金属,电子需要克服势垒;而由金属向半导体,电子受势垒阻挡。在加正向偏置时半导体一侧的势垒下降;相反,在加反向偏置时,半导体一侧势垒增高。使得金属-半导体接触具有整流作用(但不是一切金属—半导体接触均如此。如果对于P型半导体,金属的功函数大于半导体的功函数,对于N型半导体,金属的功函数小于半导体的功函数,以及半导体杂质浓度不小于10^19/立方厘米数量级时会出现欧姆接触,它会因杂质浓度高而发生隧道效应,以致势垒不起整流作用。并非所有的金属-半导体接面都是具有整流特性的,不具有整流特性的金属-半导体接面则称为欧姆接触。整流属性决定于金属的功函、固有半导体的能隙,以及半导体的掺杂类型及浓度。在设计半导体器件时需要对肖特基效应相当熟悉,以确保不会在需要欧姆接触的地方意外地产生肖特基势垒。当半导体均匀掺杂时肖特基势垒的空间电荷层宽度和单边突变P-N结的耗尽层宽度相一致。
金属与n型半导体形成的肖特基势垒如图1所示。金属—半导体作为一个整体在热平衡时有同样费米能级。肖特基势垒相较于PN接面最大的区别在于具有较低的接面电压,以及在金属端具有相当薄的(几乎不存在)空乏区宽度。由半导体到金属,电子需要克服势垒;而由金属向半导体,电子受势垒阻挡。在加正向偏置时半导体一侧的势垒下降;相反,在加反向偏置时,半导体一侧势垒增高。使得金属-半导体接触具有整流作用(但不是一切金属—半导体接触均如此。如果对于P型半导体,金属的功函数大于半导体的功函数,对于N型半导体,金属的功函数小于半导体的功函数,以及半导体杂质浓度不小于10^19/立方厘米数量级时会出现欧姆接触,它会因杂质浓度高而发生隧道效应,以致势垒不起整流作用。并非所有的金属-半导体接面都是具有整流特性的,不具有整流特性的金属-半导体接面则称为欧姆接触。整流属性决定于金属的功函、固有半导体的能隙,以及半导体的掺杂类型及浓度。在设计半导体器件时需要对肖特基效应相当熟悉,以确保不会在需要欧姆接触的地方意外地产生肖特基势垒。当半导体均匀掺杂时肖特基势垒的空间电荷层宽度和单边突变P-N结的耗尽层宽度相一致。
优点 由于肖特基势垒具有较低的界面电压,可被应用在某器件需要近似于一个理想二极管的地方。在电路设计中,它们也同时与一般的二极管及晶体管一起使用,
其主要的功能是利用其较低的接面电压来保护电路上的其它器件。
然而,自始至终肖特基器件相较于其它半导体器件来说能被应用的领域并不广。
然而,自始至终肖特基器件相较于其它半导体器件来说能被应用的领域并不广。
器件 肖特基二极管,肖特基势垒自身作为器件即为肖特基二极管。
肖特基势垒碳纳米管场效应晶体管FET:金属和碳纳米管之间的接触并不理想所以层错导致肖特基势垒,所以我们可以使用这一势垒来制作肖特基二极管或者晶体管等等。
 肖特基二极管(2张)
肖特基二极管(2张)
肖特基势垒碳纳米管场效应晶体管FET:金属和碳纳米管之间的接触并不理想所以层错导致肖特基势垒,所以我们可以使用这一势垒来制作肖特基二极管或者晶体管等等。
 肖特基二极管(2张)
肖特基二极管(2张)太阳能电池是一对光有响应并能将光能转换成电力的器件。能产生光伏效应的材料有许多种,如:单晶硅,多晶硅,非晶硅,砷化镓,硒铟铜等。它们的发电原理基本相同,现以晶体为例描述光发电过程。p型晶体硅经过掺杂磷可得n型硅,形成p-n结。
当光线照射太阳能电池表面时,一部分光子被硅材料吸收;光子的能量传递给了硅原子,使电子发生了越迁,成为自由电子在p-n结两侧集聚形成了电位差,当外部接通电路时,在该电压的作用下,将会有电流流过外部电路产生一定的输出功率。这个过程的实质是:光子能量转换成电能的过程。
当光照射到半导体上时,光子将能量提供给电子,电子将跃迁到更高的能态,在这些电子中,作为实际使用的光电器件里可利用的电子有:
(1)价带电子;
(2)自由电子或空穴(free carrier);
(3)存在于杂质能级上的电子。
太阳电池可利用的电子主要是价带电子。由价带电子得到光的能量跃迁到导带的过程决定的光的吸收称为本征或固有吸收。
太阳电池能量转换的基础是结的光生伏特效应。当光照射到pn结上时,产生电子一空穴对,在半导体内部结附近生成的载流子没有被复合而到达空间电荷区,受内建电场的吸引,电子流入n区,空穴流入p区,结果使n区储存了过剩的电子,p区有过剩的空穴。它们在pn结附近形成与势垒方向相反的光生电场。光生电场除了部分抵消势垒电场的作用外,还使p区带正电,n区带负电,在n区和p区之间的薄层就产生电动势,这就是光生伏特效应。此时,如果将外电路短路,则外电路中就有与入射光能量成正比的光电流流过,这个电流称作短路电流,另一方面,若将pn结两端开路,则由于电子和空穴分别流入n区和p区,使n区的费米能级比p区的费米能级高,在这两个费米能级之间就产生了电位差voc。可以测得这个值,并称为开路电压。由于此时结处于正向偏置,因此,上述短路光电流和二极管的正向电流相等,并由此可以决定voc的值。
太阳电池的能量转换过程
太阳电池是将太阳能直接转换成电能的器件。它的基本构造是由半导体的pn结组成。此外,异质结、肖特基势垒等也可以得到较好的光电转换效率。本节以最普通的硅pn结太阳电池为例,详细地观察光能转换成电能的情况。
首先研究使太阳电池工作时,在外部观测到的特性。当太阳光照射到这个太阳电池上时,将有和暗电流方向相反的光电流iph流过。
当给太阳电池连结负载r,并用太阳光照射时,则负载上的电流im和电压vm将由图中有光照时的电流一电压特性曲线与v=-ir表示的直线的交点来确定。此时负载上有pout=ri2m的*gong*率消耗,它清楚地表明正在进行着光电能量的转换。通过调整负载的大小,可以在一个最佳的工作点上得到最大输出*gong*率。输出*gong*率(电能)与输入*gong*率(光能)之比称为太阳电池的能量转换效率。
下面我们把目光转到太阳电池的内部,详细研究能量转换过程。太阳电池由硅pn结构成,在表面及背面形成无整流特性的欧姆接触。并假设除负载电阻r外,电路中无其它电阻成分。当具有hν(ev)(hν>eg,eg为硅的禁带宽度)能量的光子照射在太阳电池上时,产生电子―空穴对。由于光子的能量比硅的禁带宽度大,因此电子被激发到比导带底还高的能级处。对于p型硅来说,少数载流子浓度np极小(一般小于105/cm),导带的能级几乎都是空的,因此电子又马上落在导带底。这时电子及空穴将总的hν - eg(ev)的多余能量以声子(晶格振动)的形式传给晶格。落到导带底的电子有的向表面或结扩散,有的在半导体内部或表面复合而消失了。但有一部分到达结的载流子,受结处的内建电场加速而流入n型硅中。在n型硅中,由于电子是多数载流子,流入的电子按介电驰豫时间的顺序传播,同时为满足n型硅内的载流子电中性条件,与流入的电子相同数目的电子从连接n型硅的电极流出。这时,电子失去相当于空间电荷区的电位高度及导带底和费米能级之间电位差的能量。设负载电阻上每秒每立方厘米流入n个电子,则加在负载电阻上的电压v=qnr=ir表示。由于电路中无电源,电压v=ir实际加在太阳电池的结上,即结处于正向偏置。一旦结处于正向偏置时,二极管电流id=i0[exp(qv/nkt)-1]朝着与光激发产生的载流子形成的光电流iph相反的方向流动,因而流入负载电阻的电流值为
在负载电阻上,一个电子失去一个qv的能量,即等于光子能量hν转换成电能qv。流过负载电阻的电子到达p型硅表面电极处,在p型硅中成为过剩载流子,于是和被扫出来的空穴复合,形成光电流
肖特基二极管是以金属为正极,N型半导体为负极,利用二者接触面上形成的势垒,从而具有整流特性的金属-半导体器件。因此它不是P-N结,而是金属-N结。由于金属导体内部有大量的导电电子,使得金属的费米能级低于半导体的费米能级,所以当金属与半导体接触时,形成的势垒高度低于PN结势垒高度,势垒高度低的外在表现为正向导通压降小,因而损耗小。
就一个由费米子组成的微观体系而言,每个费米子都处在各自的量子能态上。现在假想 把所有的费米子
从这些量子态上移开。之后再把这些费米子按照一定的规则(例如泡利原理等)填充在各个可供占据的量子能态上,并且这种填充过程中每个费米子都占据
最低的可供占据的量子态。最后一个费米子占据着的量子态 即可粗略理解为费米能级。
虽然严格来说,费米能等于费米子系统在趋于绝对零度时的化学势;但是在半导体物理和电子学领域中,费米能级则经常被当做电子或空穴化学势的代名词。一般来说,“费米能级"这个术语所代表的含义可以从上下语境中判断。
费米子[1]可以是电子、质子、中子(自旋为半整数的粒子)
对于金属,绝对零度下,电子占据的最高能级就是费米能级。
费米能级的物理意义是,该能级上的一个状态被电子占据的几率是1/2。
费米能级在半导体物理中是个很重要的物理参数,只要知道了他的数值,在一定温度下,电子在各量子态上的统计分布就完全确定了。它和温度,半导体材料的导电类型,杂质的含量以及能量零点的选取有关。
将半导体中大量电子的集体看成一个热力学系统,可以证明处于热平衡状态下的电子系统有统一的费米能级。
费米子[1]可以是电子、质子、中子(自旋为半整数的粒子)
对于金属,绝对零度下,电子占据的最高能级就是费米能级。
费米能级的物理意义是,该能级上的一个状态被电子占据的几率是1/2。
费米能级在半导体物理中是个很重要的物理参数,只要知道了他的数值,在一定温度下,电子在各量子态上的统计分布就完全确定了。它和温度,半导体材料的导电类型,杂质的含量以及能量零点的选取有关。
将半导体中大量电子的集体看成一个热力学系统,可以证明处于热平衡状态下的电子系统有统一的费米能级。
在固态物理学中,一个由无相互作用的费米子组成的系统的费米能(EF)表示在该系统中加入一个粒子引起的基态能量的最小可能增量。费米能亦可等价定义为在绝对零度时,处于基态的费米子系统的化学势,或上述系统中处于基态的单个费米子的最高能量。费米能是凝聚态物理学的核心概念之一。
虽然严格来说,费米能级是指费米子系统在趋于绝对零度时的化学位;但是在半导体物理和电子学领域中,费米能级则经常被当做电子或空穴化学势的代名词。一般来说,“费米能级"这个术语所代表的含义可以从上下语境中判断。
费米能以提出此概念的美籍意大利裔物理学家恩里科·费米(Enrico Fermi)的名字命名。
虽然严格来说,费米能级是指费米子系统在趋于绝对零度时的化学位;但是在半导体物理和电子学领域中,费米能级则经常被当做电子或空穴化学势的代名词。一般来说,“费米能级"这个术语所代表的含义可以从上下语境中判断。
费米能以提出此概念的美籍意大利裔物理学家恩里科·费米(Enrico Fermi)的名字命名。
三维形式的推导
考虑一个处于边长为L 的正方体内无相互作用的费米子组成的系统,其总体积 V = L3。该系统的波函数可视为限制于三维无限深方形阱中,可写为:

其中
A 为波函数的归一化常数,
nx、ny、nz 为正整数
在某一能级上一个粒子的能量为:

在绝对零度时,该费米子系统中存在具有最高能量即费米能的一个粒子,将该粒子所处的态记为nF。对于具有N 个费米子的系统,其nF 须满足:

或简化为

带入En 能量式,即得到费米能的表达式:



利用几何关系(将L2 写成V2/3),既得到用单位体积中的粒子数表示的费米能:

其中
 为约化普朗克常数
为约化普朗克常数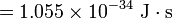
m 为粒子质量。
考虑一个处于边长为L 的正方体内无相互作用的费米子组成的系统,其总体积 V = L3。该系统的波函数可视为限制于三维无限深方形阱中,可写为:
其中
A 为波函数的归一化常数,
nx、ny、nz 为正整数
在某一能级上一个粒子的能量为:
在绝对零度时,该费米子系统中存在具有最高能量即费米能的一个粒子,将该粒子所处的态记为nF。对于具有N 个费米子的系统,其nF 须满足:
或简化为
带入En 能量式,即得到费米能的表达式:
利用几何关系(将L2 写成V2/3),既得到用单位体积中的粒子数表示的费米能:

其中
m 为粒子质量。
典型的费米能
[编辑] 白矮星
白矮星是宇宙中一类质量与太阳相当,但半径约只有太阳的1/100的天体。这种天体的高密度使的其中的电子不是被各自所属的单个原子核束缚,而是以简并电子气的形式存在。白矮星中的体积电子数密度为1036个/m3 量级。利用前面的公式可以得到其费米能为:

[编辑] 原子核
另一个典型例子是构成原子核的核子(即质子和中子)。原子核半径约为:

其中 A 为核子数。
所以原子核的核子数密度为:
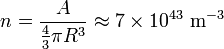
所以原子核的费米能约为:
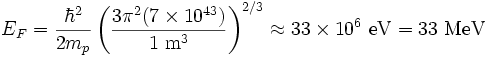
[编辑] 白矮星
白矮星是宇宙中一类质量与太阳相当,但半径约只有太阳的1/100的天体。这种天体的高密度使的其中的电子不是被各自所属的单个原子核束缚,而是以简并电子气的形式存在。白矮星中的体积电子数密度为1036个/m3 量级。利用前面的公式可以得到其费米能为:

[编辑] 原子核
另一个典型例子是构成原子核的核子(即质子和中子)。原子核半径约为:
其中 A 为核子数。
所以原子核的核子数密度为:
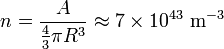
所以原子核的费米能约为:
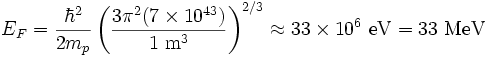
费米能级是绝对零度下电子的最高能级。根据泡利不相容原理,同一个量子态不能容纳两个或两个以上的费米子,所以在绝对零度下,电子将从低到高依次填充各能级,形成电子能态的“费米海”[1]。“费米海”中每个电子的平均能量为(绝对零度下):

其中 EF 为费米能。
费米面上电子(或其它费米子)的动量称为费米动量,满足:

其中 me 为电子质量。
这个概念通常应用在能量和动量之间的色散关系上,与动量的方向无关。更一般的情况下,费米能更具有普遍意义。
费米速度指绝对零度下电子绕原子核运动的平均速度,该速度对应于前面给出的平均能量。费米速度定义为:

其中 me 为电子质量。
另一个相关的概念是费米温度,定义为:

其中 kB 为玻尔兹曼常数。
物质在费米温度以下会越来越显著地表现出量子效应。
其中 EF 为费米能。
费米面上电子(或其它费米子)的动量称为费米动量,满足:
其中 me 为电子质量。
这个概念通常应用在能量和动量之间的色散关系上,与动量的方向无关。更一般的情况下,费米能更具有普遍意义。
费米速度指绝对零度下电子绕原子核运动的平均速度,该速度对应于前面给出的平均能量。费米速度定义为:

其中 me 为电子质量。
另一个相关的概念是费米温度,定义为:
其中 kB 为玻尔兹曼常数。
物质在费米温度以下会越来越显著地表现出量子效应。
量子力学解释
根据量子力学理论,具有半奇数自旋量子数(通常为1/2)的费米子,如电子,遵循泡利不相容原理,即一个量子态只能被一个粒子所占据。因此,费米子在能级中的分布遵循费米-狄拉克分布。一个由无相互作用的费米子组成的系统的基态模型可按照如下的方法构造:从无粒子系统开始,将粒子逐个填入现有而未被占据的最低能量的量子态,直到所有粒子全部填完。此时,系统的费米能就是最高占据分子轨道(highest occupied molecular orbital,缩写为HOMO)的能量。在导电材料中,HOMO与最低未占据分子轨道(lowest unoccupied molecular orbital,缩写为LUMO)是等价的。但在其它材料中,上述两个轨道的能量会相差2-3电子伏。事实上这一能隙在导体中也存在,只是小得可以忽略而已。
根据量子力学理论,具有半奇数自旋量子数(通常为1/2)的费米子,如电子,遵循泡利不相容原理,即一个量子态只能被一个粒子所占据。因此,费米子在能级中的分布遵循费米-狄拉克分布。一个由无相互作用的费米子组成的系统的基态模型可按照如下的方法构造:从无粒子系统开始,将粒子逐个填入现有而未被占据的最低能量的量子态,直到所有粒子全部填完。此时,系统的费米能就是最高占据分子轨道(highest occupied molecular orbital,缩写为HOMO)的能量。在导电材料中,HOMO与最低未占据分子轨道(lowest unoccupied molecular orbital,缩写为LUMO)是等价的。但在其它材料中,上述两个轨道的能量会相差2-3电子伏。事实上这一能隙在导体中也存在,只是小得可以忽略而已。
自由电子气
自由电子气是借用理想气体模型描述费米子系统性质的量子力学模型。该模型中,粒子所处的量子态可用它们具有的动量来表征。对于周期性系统,譬如在金属原子点阵中运动的电子,亦可类似地引入“准动量”的概念以表征量子态(参见条目布洛赫波)。无论上述哪种模型,其具有费米能的量子态都处于动量空间中的一个确定的曲面上,这个曲面称为费米面。自由电子气的费米面是一个球面;周期体系中的费米面则通常是扭曲面(参见条目布里渊区)。费米面包围的体积决定了系统中的电子数,而费米面的拓扑结构则与金属的各种传导性质(如电导率)直接相关。对费米面的研究有时被称为“费米学”(Fermiology)。如今,绝大多数金属的费米面均已经有较透彻的理论与实验研究。
自由电子气的费米能与化学势之间存在如下关系:
 "
"
]其中 EF 为费米能,kB 为玻尔兹曼常数,T 为绝对温度。从上式可以看出,当温度远低于费米温度EF/kB时,系统的化学势与费米能近似相等。金属的费米温度为105K量级,因此在室温(300 K)下,系统的费米能与化学势基本上是相等的。这在应用上是一个重要的结论,因为费米-狄拉克分布的表达式中出现的是化学势,而不是费米能[1]
自由电子气是借用理想气体模型描述费米子系统性质的量子力学模型。该模型中,粒子所处的量子态可用它们具有的动量来表征。对于周期性系统,譬如在金属原子点阵中运动的电子,亦可类似地引入“准动量”的概念以表征量子态(参见条目布洛赫波)。无论上述哪种模型,其具有费米能的量子态都处于动量空间中的一个确定的曲面上,这个曲面称为费米面。自由电子气的费米面是一个球面;周期体系中的费米面则通常是扭曲面(参见条目布里渊区)。费米面包围的体积决定了系统中的电子数,而费米面的拓扑结构则与金属的各种传导性质(如电导率)直接相关。对费米面的研究有时被称为“费米学”(Fermiology)。如今,绝大多数金属的费米面均已经有较透彻的理论与实验研究。
自由电子气的费米能与化学势之间存在如下关系:
]其中 EF 为费米能,kB 为玻尔兹曼常数,T 为绝对温度。从上式可以看出,当温度远低于费米温度EF/kB时,系统的化学势与费米能近似相等。金属的费米温度为105K量级,因此在室温(300 K)下,系统的费米能与化学势基本上是相等的。这在应用上是一个重要的结论,因为费米-狄拉克分布的表达式中出现的是化学势,而不是费米能[1]
- 有15篇回复贴





No comments:
Post a Comment