阿布拉罕-勞侖茲力(Abraham-Lorentz force)是一加速
帶電粒子因為粒子放射出
電磁輻射而所受到的平均
力。其適用在粒子行進速度不快的時候。若在
相對論性速度下,此力則稱作是
阿布拉罕-勞侖茲-狄拉克力(Abraham-Lorentz-Dirac force)。
阿布拉罕-勞侖茲力問題的解被認為預測了「來自於未來的訊號影響了現在」這樣的結果,而挑戰了直觀上的因果律。試圖解決此一問題的涉及到許多
近代物理的領域,雖然Yaghjian曾展試過這問題的解實際上相當簡單。
定義與描述[编辑]
數學上,阿布拉罕-勞侖茲力可寫為:
其中:
- F 是力,
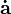 是 加加速度(加速度的导数)。
是 加加速度(加速度的导数)。
- μ0和ε0 是真空磁导率和真空电容率,
- c是真空中的光速,
- q 是电荷量。
當速度很慢時。根據
拉莫方程式(Larmor formula),一加速電荷放出輻射,而輻射會將
動量自電荷帶走。既然動量是
守恆的,電荷會被推往與輻射釋放方向相反的方向。阿布拉罕-勞侖茲力即為因於輻射釋放而施加在一加速電荷上的平均力。
古典電動力學中,問題通常可以分為兩類:
- 問題中,產生場的電荷與電流源已指定,要計算出場;
- 問題中,場已指定,要計算出電荷的運動。
在一些物理學領域中,如
電漿物理學,場由源產生,而源的運動可以自洽的解出。然而在這樣的場合中,源的運動常是從所有其他的源產生的場來計算。很少去計算一粒子(源)所產生的場,對於同一粒子造成什麼樣的運動影響。理由有兩個層次:
- 忽略「自身場(self-fields)」通常仍可得到足夠精確的答案,足以用在許多應用上;
- 包含自身場會導致物理學中目前未解決的問題,關係到物質與能量的本質。
由自身場所衍生的概念問題在標準的研究生教科書有所著墨。(
Jackson電動力學)
“
(譯自原文)此一問題所引出的困難涉及到物理學中最重要的基本面貌之一──基本粒子的本質。雖然在一些設有限制的領域中,有部份可用的解已經給出,然則基本問題方面則仍舊未有解決。一些人可能希望從古典到量子處理方法上的過渡可以解決這樣的難題。雖仍希望這件事終究會發生,不過當前量子力學方面的討論甚至還遇上了比古典還要複雜得多的狀況。在較近期的年代中(~
1948年 -
1950年),所出現的成就之一是將
勞侖茲協變性與
規範不變性等概念巧妙地運用,在
量子電動力學中迴避了這些困難,而允許對於非常小的輻射效應做出計算,達到極高的精準度,並與實驗結果相符。但若從基本觀點來看,這樣的難題依舊是存在的。
”
我们从点电荷的辐射的
拉莫方程式开始:
 .
.
如果我们假设带电粒子的运动是周期性的,则阿布拉罕-洛伦兹力对粒子所做的功等于拉莫功率从
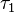
到

的积分:
 .
.
我们可以用
分部积分法来计算以上的积分。如果我们假设运动是周期性的,则表达式的第一项为零:
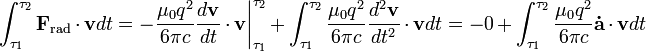 .
.
因此,我们有:
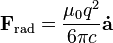 .
.
来自未来的讯号[编辑]
下面展示了一种会导致惊人结果的经典分析方法。可以看到,经典理论正在挑战因果律的标准图景,表明要么因果律被破坏,要么理论需要扩展。在本例中,理论的扩展包括
量子力学和它的相对论版本
量子场论。参考Rohrlich
[1]关于“物理学理论遵循有效性限制的重要性”的介绍。
对于一个受到外力

,我们有

其中:
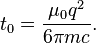
公式经过整理后,可以得到:

这个积分从当前延续到无穷远的未来。因而未来的作用力将影响到粒子当前的加速度。未来的数值按以下因子加权:

随着未来超过
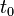
时间的增长而迅速减小。因此,大概在未来
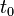
时间段内的信号会影响到当前的加速度。对于电子来说,这个时间段大约是

秒,相当于光线穿越电子“尺寸”所需的时间。
 .
.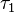 到
到 的积分:
的积分: .
.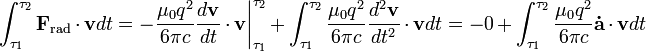 .
.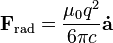 .
. ,我们有
,我们有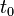 时间的增长而迅速减小。因此,大概在未来
时间的增长而迅速减小。因此,大概在未来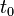 时间段内的信号会影响到当前的加速度。对于电子来说,这个时间段大约是
时间段内的信号会影响到当前的加速度。对于电子来说,这个时间段大约是 秒,相当于光线穿越电子“尺寸”所需的时间。
秒,相当于光线穿越电子“尺寸”所需的时间。 (
( (
(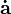 是
是 
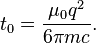


No comments:
Post a Comment