访客
博文
标签:
杂谈 |
算术平方根是一个非负数的非负平方根。
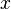 的平方根是
的平方根是 ,它的算术平方根是
,它的算术平方根是 。
。
再如4的平方根是±2,它的算术平方根是2。
0的算术平方根是0。
方差
 是随机变量
X 的期望值(平均数)设
是随机变量
X 的期望值(平均数)设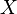 为服从分布
为服从分布 的随机变量,则称
的随机变量,则称
 为随机变量
为随机变量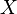 或者分布
或者分布 的方差。
的方差。
如果X是一个复数随机变量的向量(向量中每个元素均为复数的随机变量),那么其方差定义则为E[(X − μ)(X − μ)*],其中X*是X的共轭转置向量或称为埃尔米特向量。根据这个定义,方差为实数。
标准差的观念是由卡尔·皮尔逊(Karl Pearson)引入到统计中。
例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
 (皆为实数),其平均值为:
(皆为实数),其平均值为:
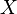 的标准差定义为:
的标准差定义为:
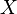 为
为  具有相同概率,则可用上述公式计算标准差。
具有相同概率,则可用上述公式计算标准差。
从一大组数值 当中取出一样本数值组合
当中取出一样本数值组合
 ,常定义其样本标准差:
,常定义其样本标准差:
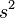 是对总体方差
是对总体方差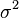 的无偏估计。
的无偏估计。  中分母为
中分母为 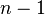 是因为
是因为  的自由度为
的自由度为 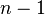 ,这是由于存在约束条件
,这是由于存在约束条件  。
。
 的连续随机变量
的连续随机变量 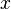 的标准差是:
的标准差是:
 和随机变量
和随机变量 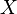 和
和  :
:
第一步,计算平均值 ︰
︰
 = 4 (因为集合里有 4 个数),分别设为:
= 4 (因为集合里有 4 个数),分别设为:
 ︰
︰
 在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约 68% 数值分布在距离平均值有 1 个标准差之内的范围,约 95%
数值分布在距离平均值有 2 个标准差之内的范围,以及约 99.7% 数值分布在距离平均值有 3 个标准差之内的范围。称为
"68-95-99.7法则"。
在实际应用上,常考虑一组数据具有近似于正态分布的概率分布。若其假设正确,则约 68% 数值分布在距离平均值有 1 个标准差之内的范围,约 95%
数值分布在距离平均值有 2 个标准差之内的范围,以及约 99.7% 数值分布在距离平均值有 3 个标准差之内的范围。称为
"68-95-99.7法则"。
 为实数,定义函数
为实数,定义函数
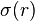 在下面情况下具有唯一最小值:
在下面情况下具有唯一最小值:
 维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值,
维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值, 。它们可以在3维空间中确定一个点
。它们可以在3维空间中确定一个点  。想像一条通过原点的直线
。想像一条通过原点的直线 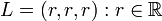 。如果这组数据中的3个值都相等,则点
。如果这组数据中的3个值都相等,则点 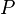 就是直线
就是直线  上的一个点,
上的一个点,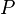 到
到  的距离为0, 所以标准差也为0。若这3个值不都相等,过点
的距离为0, 所以标准差也为0。若这3个值不都相等,过点 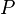 作垂线
作垂线  垂直于
垂直于  ,
, 交
交  于点
于点  ,则
,则  的坐标为这3个值的平均数:
的坐标为这3个值的平均数:
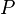 与点
与点  之间的距离(也就是点
之间的距离(也就是点 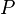 到直线
到直线  的距离)是
的距离)是 。在
。在
 维空间中,这个规律同样适用,把
维空间中,这个规律同样适用,把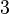 换成
换成
 就可以了。
就可以了。
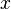 的平方根是
的平方根是 ,它的算术平方根是
,它的算术平方根是 。
。再如4的平方根是±2,它的算术平方根是2。
0的算术平方根是0。
方差
目录[隐藏] |
定义
如果 是随机变量
X 的期望值(平均数)设
是随机变量
X 的期望值(平均数)设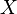 为服从分布
为服从分布 的随机变量,则称
的随机变量,则称 为随机变量
为随机变量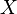 或者分布
或者分布 的方差。
的方差。特性
在样本空间Ω上存在有限期望和方差的随机变量构成一个希尔伯特空间: L2(Ω, dP),不过这里的内积和长度跟方差,标准差还是不大一样。所以,我们得把这个空间“除”常变量构成的子空间,也就是说把相差一个常数的所有原来那个空间的随机变量做成一个等价类。这还是一个新的无穷维线性空间,并且有一个从老空间内积诱导出来的新内积,而这个内积就是方差一般化
如果X是一个向量其取值范围在实数空间Rn,并且其每个元素都是一个一维随机变量,我们就把X称为随机向量。随机向量的方差是一维随机变量方差的自然推广,其定义为E[(X − μ)(X − μ)T],其中μ = E(X),XT是X的转秩.这个方差是一个非负定的方阵,通常称为协方差矩阵。如果X是一个复数随机变量的向量(向量中每个元素均为复数的随机变量),那么其方差定义则为E[(X − μ)(X − μ)*],其中X*是X的共轭转置向量或称为埃尔米特向量。根据这个定义,方差为实数。
标准差
标准差(Standard Deviation),在概率统计中最常使用作为统计分布程度(statistical dispersion)上的测量。标准差定义为方差的算术平方根,反映组内个体间的离散程度。测量到分布程度的结果,原则上具有两种性质:
- 为非负数值,
- 与测量资料具有相同单位。
标准差的观念是由卡尔·皮尔逊(Karl Pearson)引入到统计中。
目录[显示] |
阐述及应用
简单来说,标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。例如,两组数的集合 {0, 5, 9, 14} 和 {5, 6, 8, 9} 其平均值都是 7 ,但第二个集合具有较小的标准差。
标准差可以当作不确定性的一种测量。例如在物理科学中,做重复性测量时,测量数值集合的标准差代表这些测量的精确度。当要决定测量值是否符合预测值,测量值的标准差占有决定性重要角色:如果测量平均值与预测值相差太远(同时与标准差数值做比较),则认为测量值与预测值互相矛盾。这很容易理解,因为如果测量值都落在一定数值范围之外,可以合理推论预测值是否正确。
标准差应用于投资上,可作为量度回报稳定性的指标。标准差数值越大,代表回报远离过去平均数值,回报较不稳定故风险越高。相反,标准差数值越小,代表回报较为稳定,风险亦较小。
标准差的定义及简易计算公式
标准计算公式
假设有一组数值 (皆为实数),其平均值为:
(皆为实数),其平均值为: .
.
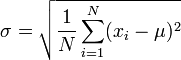 .
.
简化计算公式
上述公式可以变换为一个较简单的公式:随机变量的标准差计算公式
一随机变量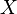 的标准差定义为:
的标准差定义为: .
.
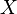 为
为  具有相同概率,则可用上述公式计算标准差。
具有相同概率,则可用上述公式计算标准差。样本标准差
在真实世界中,除非在某些特殊情况下,找到一个总体的真实的标准差是不现实的。大多数情况下,总体标准差是通过随机抽取一定量的样本并计算样本标准差估计的。从一大组数值
 当中取出一样本数值组合
当中取出一样本数值组合
 ,常定义其样本标准差:
,常定义其样本标准差: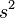 是对总体方差
是对总体方差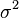 的无偏估计。
的无偏估计。  中分母为
中分母为 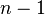 是因为
是因为  的自由度为
的自由度为 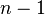 ,这是由于存在约束条件
,这是由于存在约束条件  。
。连续随机变量的标准差计算公式
概率密度为 的连续随机变量
的连续随机变量 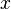 的标准差是:
的标准差是:标准差的性质
对于常数 和随机变量
和随机变量 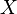 和
和  :
:


- 其中:
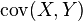 表示随机变量
表示随机变量 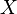 和
和  的协方差。
的协方差。
范例
这里示范如何计算一组数的标准差。例如一群孩童年龄的数值为 { 5, 6, 8, 9 } :第一步,计算平均值
 ︰
︰ = 4 (因为集合里有 4 个数),分别设为:
= 4 (因为集合里有 4 个数),分别设为: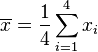 用 4 取代
用 4 取代 
 此为平均值。
此为平均值。
 ︰
︰ 用 4 取代
用 4 取代 
 用 7 取代
用 7 取代 
 此为标准差。
此为标准差。
正态分布的规则

深蓝区域是距平均值小于一个标准差之内的数值范围。在正态分布中,此范围所占比率为全部数值之 68% 。 根据正态分布,两个标准差之内(深蓝,蓝)的比率合起来为 95%
。根据正态分布,三个标准差之内(深蓝,蓝,浅蓝)的比率合起来为 99% 。
标准差与平均值之间的关系
一组数据的平均值及标准差常常同时作为参考的依据。从某种意义上说,如果用平均值来考量数值的中心的话,则标准差也就是对统计的分散度的一个"自然"的测度。因为由平均值所得的标准差要小于到其他任何一个点的标准差。较确切的叙述为:设 为实数,定义函数
为实数,定义函数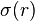 在下面情况下具有唯一最小值:
在下面情况下具有唯一最小值:几何学解释
从几何学的角度出发,标准差可以理解为一个从 维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值,
维空间的一个点到一条直线的距离的函数。举一个简单的例子,一组数据中有3个值, 。它们可以在3维空间中确定一个点
。它们可以在3维空间中确定一个点  。想像一条通过原点的直线
。想像一条通过原点的直线 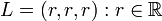 。如果这组数据中的3个值都相等,则点
。如果这组数据中的3个值都相等,则点 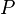 就是直线
就是直线  上的一个点,
上的一个点,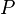 到
到  的距离为0, 所以标准差也为0。若这3个值不都相等,过点
的距离为0, 所以标准差也为0。若这3个值不都相等,过点 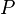 作垂线
作垂线  垂直于
垂直于  ,
, 交
交  于点
于点  ,则
,则  的坐标为这3个值的平均数:
的坐标为这3个值的平均数: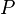 与点
与点  之间的距离(也就是点
之间的距离(也就是点 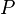 到直线
到直线  的距离)是
的距离)是 。在
。在
 维空间中,这个规律同样适用,把
维空间中,这个规律同样适用,把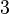 换成
换成
 就可以了。
就可以了。标签:
杂谈 |
算术-几何平均数
两个正实数x和y的算术-几何平均数定义如下:
首先计算x的y算术平均数,称其为a1。然后计算x的y几何平均数,称其为g1;这是xy的平方根。
如果r > 0,则M(rx, ry) = r M(x, y)。
M(x,y)还可以写为如下形式:
1和 的算术-几何平均数的倒数,称为高斯常数。
的算术-几何平均数的倒数,称为高斯常数。
首先计算x的y算术平均数,称其为a1。然后计算x的y几何平均数,称其为g1;这是xy的平方根。
目录[隐藏] |
[编辑] 例子
欲计算a0 = 24和g0 = 6的算术-几何平均数,首先算出它们的算术平均数和几何平均数: etc.
etc.
-
n an gn 0 24 6 1 15 12 2 13.5 13.41640786500... 3 13.45820393250... 13.45813903099... 4 13.45817148175... 13.45817148171...
[编辑] 性质
M(x, y)是一个介于x和y的算术平均数和几何平均数之间的数。如果r > 0,则M(rx, ry) = r M(x, y)。
M(x,y)还可以写为如下形式:
1和
 的算术-几何平均数的倒数,称为高斯常数。
的算术-几何平均数的倒数,称为高斯常数。[编辑] 参见
[编辑] 参考文献
- Jonathan Borwein, Peter Borwein, Pi and the AGM. A study in analytic number theory and computational complexity. Reprint of the 1987 original. Canadian Mathematical Society Series of Monographs and Advanced Texts, 4. A Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1998. xvi+414 pp. ISBN 0-471-31515-X MR1641658
- Eric W. Weisstein, Arithmetic-Geometric mean, MathWorld.
标签:
杂谈 |
是统计中的一个重要概念。为集中趋势的最常用测度值,目的是确定一组数据的均衡点。
算术平均数是表征数据集中趋势的一个统计指标。它是一组数据之和除以这组数据之个/项数。
算术平均数在统计学上的优点就是它较中位数、众数更少受到随机因素影响,缺点是它更容易受到极端数影响。
计算公式为:
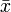 表示,对全体数据的平均值用
表示,对全体数据的平均值用  表示。
表示。几何平均数,是求一组数值的平均数的方法中的一种。适用于对比率数据的平均,并主要用于计算数据平均增长(变化)率。
其计算公式为:
标签:
杂谈 |
曲面积分
曲面积分http://v.youku.com/v_show/id_XMTY1NzQwNzY4.html
曲面应满足什么条件才能使高斯公式成立?曲面应是分片光滑的闭曲面!!!
Gauss公式的实质
表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系.
物理意义----通量与散度
向量场
曲线积分和曲面积分的物理意义是什么啊?
变力做功的问题就是一个典型的曲线积分问题。
电通量和磁通量问题就是一个典型的曲面积分问题。
对于矢量而言,
闭合曲线积分:环流;
闭合曲面积分:通量。
闭合曲线上的斯托克斯积分,揭示了什么样的物理现象?
有旋还是无旋
高斯散度定理
更加精确地说,高斯公式说明向量场穿过曲面的通量,等于曲面内部区域的散度的三重积分。直观地,所有源点的和减去所有汇点的和,就是流出一个区域的流量。
高斯公式在工程数学中是一个很重要的结果,特别是静电学和流体力学。
这两个公式叫做高斯公式。
 是定义在V中和S上连续可微的矢量场。如果
是定义在V中和S上连续可微的矢量场。如果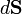 是外法向矢量面元,则
是外法向矢量面元,则
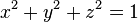 所定义的单位球,F是向量场
所定义的单位球,F是向量场
 和
和 是奇函数,我们有:
是奇函数,我们有:
 。
。
下面举一个例子:用二阶张量及其与矢量的缩并来重新写 和
和 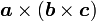 。
。
 的转置
的转置  (又可以记为
(又可以记为  ),定义如下:
),定义如下:
 是三维欧几里得空间中的一个有限区域,
是三维欧几里得空间中的一个有限区域, 是它的边界曲面,
是它的边界曲面,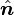 是
是  的外法线方向上的单位矢量,
的外法线方向上的单位矢量, 是定义在
是定义在  的某个开邻域上的
的某个开邻域上的  连续的二阶张量场,
连续的二阶张量场, 是
是  的转置,则
的转置,则
 ,则
,则
数学上,曲面积分(面积分)是在曲面上的定积分(曲面可以是空间中的弯曲子集);它可以视为和线积分相似的双重积分。给定一个曲面,可以在上面对标量场(也即,返回数值的函数)进行积分,也可以对向量场(也即,返回向量值的函数)积分。
面积分在物理中有大量应用,特别是在电磁学的经典理论中。
要找到面积分的直接公式,首先需要参数化S,也即在S上建立曲线坐标系,就像球面上的经纬度。令参数化为x(s, t),其中(s, t)在某个平面上的区域T中变化。则面积分为
例如,如果要找出某个函数( )形状的曲面面积,就有
)形状的曲面面积,就有
 。所以,
。所以, ,且
,且 。因此
。因此
注意,因为叉积的存在,上述供述只在曲面嵌入在三维空间中时适用。
这个解释意味着如果向量场和S在每点相切,则流量为0,因为液体平行于S流动,从而不进不出。这也意味着如果v不仅仅沿着S流动,也即,如果v既有切向分量也有法向分量,则只有法向分量对流量作出贡献。基于这个推理,要找出流量,我们必须取v和S上每点的单位法向量的点积,这就给出了一个标量场,然后就可以用上述方式积分。公式如下
该公式定义为向量场v在S上的面积分。
 。则f在S上的面积分为
。则f在S上的面积分为
注意2-形式的面积分和以 、
、 和
和 为分量的向量场的面积分相同。
为分量的向量场的面积分相同。
对于向量场,情况复杂一些,因为涉及到曲面的法向量。如果两个参数化下法向量的定向相同,则积分值不变。如果法向量定向相反,则积分值相反。因此,不必拘泥于特定参数化,但是对于向量场,参数化的定向必须保持一致。
另外一个问题是,有时曲面没有覆盖整个曲面的单一参数化;譬如对于有限长的圆柱面就是这样。一个直接的解决办法就是将曲面切成几片,在每一片上求面积分,然后加起来。这就是正确的办法,但是对向量场积分的时候,必须小心,要让每个小片的法向量定向和周围的一致。对于柱面来讲,也就是让所有片的法向量向外指。
最后一个问题是,有些曲面没有一个一致的法向量(譬如莫比乌斯带)。对于这样的曲面,无法找到一致的定向。这样的曲面称为不可定向的,在其上无法进行向量场的积分。
面积分在物理中有大量应用,特别是在电磁学的经典理论中。
标量场的面积分
考虑定义了标量场f的一个曲面S。如果把S当作某种材料制成,而对于每个点x,f(x)就是在该点的材料密度,则f在S上的面积分就是S的每单位厚度的质量。(这只当曲面是无穷薄的情况下成立。)计算面积分的一个办法是将曲面分成很多小片,假设每片的密度大致为常数,找到每片的每单位厚度质量,然后乘以小片的面积,最后加起来得到总的每单位厚度的质量。要找到面积分的直接公式,首先需要参数化S,也即在S上建立曲线坐标系,就像球面上的经纬度。令参数化为x(s, t),其中(s, t)在某个平面上的区域T中变化。则面积分为
例如,如果要找出某个函数(
 )形状的曲面面积,就有
)形状的曲面面积,就有 。所以,
。所以, ,且
,且 。因此
。因此注意,因为叉积的存在,上述供述只在曲面嵌入在三维空间中时适用。
向量场的面积分
考虑S上的向量场v,对于每个S上的点x,v(x)是一个向量。想象一个穿过S的液体流,使得v(x)决定液体在x的速度。则流量定义为单位时间穿过S的液体量。这个解释意味着如果向量场和S在每点相切,则流量为0,因为液体平行于S流动,从而不进不出。这也意味着如果v不仅仅沿着S流动,也即,如果v既有切向分量也有法向分量,则只有法向分量对流量作出贡献。基于这个推理,要找出流量,我们必须取v和S上每点的单位法向量的点积,这就给出了一个标量场,然后就可以用上述方式积分。公式如下
该公式定义为向量场v在S上的面积分。
微分2-形式的面积分
令 。则f在S上的面积分为
。则f在S上的面积分为注意2-形式的面积分和以
 、
、 和
和 为分量的向量场的面积分相同。
为分量的向量场的面积分相同。涉及面积分的定理
面积分中很多有用的结果可以用微分几何和向量微积分导出,例如散度定理及其推广斯托克斯定理。进阶问题
注意面积分的定义中用到曲面S的参数化。而给定曲面可以有多种参数化。例如,如果移动球面上南极和北极的位置,所有球面上的点的经度和纬度都会改变。很自然就有面积分是否依赖于给定参数化的问题。对于标量场的积分,答案很简单:无论参数化为何,面积分不变。对于向量场,情况复杂一些,因为涉及到曲面的法向量。如果两个参数化下法向量的定向相同,则积分值不变。如果法向量定向相反,则积分值相反。因此,不必拘泥于特定参数化,但是对于向量场,参数化的定向必须保持一致。
另外一个问题是,有时曲面没有覆盖整个曲面的单一参数化;譬如对于有限长的圆柱面就是这样。一个直接的解决办法就是将曲面切成几片,在每一片上求面积分,然后加起来。这就是正确的办法,但是对向量场积分的时候,必须小心,要让每个小片的法向量定向和周围的一致。对于柱面来讲,也就是让所有片的法向量向外指。
最后一个问题是,有些曲面没有一个一致的法向量(譬如莫比乌斯带)。对于这样的曲面,无法找到一致的定向。这样的曲面称为不可定向的,在其上无法进行向量场的积分。
参看
曲面积分
什么是曲面积分?
先看一个例子:设有一构件占空间曲面Σ,其质量分布密度函数为(密度分布)ρ(x,y,z),求构件的质量。 同样,对于密度不均匀的物件,也不可以直接利用ρS(这里的S代表的是面积,下同)处理问题的思想方法类似于分布在平面区域的质量问题,就需要利用曲面积分; dm=ρ(x,y,z)*ds;m=∫ρ(x,y,z)*ds,就是对面积的曲面积分。曲面积分的类别:
对面积的曲面积分(第一类曲面积分); 对坐标轴的曲面积分(第二类曲面积分); 对面积的曲面积分和对坐标轴的曲面积分是可以转化的;两类曲面积分的区别在于形式上积分元素的不同,第一类曲面积分的积分元素是面积元素dS,例如:在积分曲面Σ上的对面积的曲面积分: ∫∫f(x,y,z)dS; 而第二类曲面积分的积分元素是坐标平面dxdy,dydz或dxdz,例如:在积分曲面Σ上的对坐标平面的曲面积分: ∫∫P(x,y,z)dxdy+Q(x,y,z)dydz+R(x,y,z)dxdz;两种曲面积分之间的关系:
两种积分之间的转化在于如何将空间曲面在坐标平面上投影; 设dS是积分曲面Σ上的面积元素。 设Σ的方程为z=(x,y),Σ在xOy平面上的投影区域D是有界闭区域,z=(x,y)在D上具有连续的偏导数,于是: dS/(dxdy)=1/cosθ,θ是面积元素dS和坐标平面的夹角; 积分曲面Σ上任意一点的法向量为(〥z/〥x,〥z/〥y,-1)(注:〥表示求偏导数,〥z/〥x表示z对x偏导数,是整体符号,下同),xOy平面的法向量取(0,0,1); 于是1/cosθ=√[1+(〥z/〥x)^2+(〥z/〥y)^2]; 所以dS=√[1+(〥z/〥x)^2+(〥z/〥y)^2]*dxdy,Σ上的点为(x,y,z(x,y))则∫∫f(x,y,z)dS存在,且在积分曲面Σ上的曲面积分有: ∫∫f(x,y,z)dS=∫∫f(x,y,z)*√[1+(〥z/〥x)^2+(〥z/〥y)^2]*dxdy 这样就把对面积的曲面积分和对坐标轴的曲面积分的关系联系起来了。 而对于∫∫P(x,y,z)dxdy+Q(x,y,z)dydz+R(x,y,z)dxdz这种类型的曲面积分,积分曲面可能需要同时向三个坐标平面 xOy,xOz,yOz投影,投影的方式和上面的方法一样。实际上如果面积元素dS与三个坐标平面的夹角分别为α,β,γ,则有dxdy=cosαdS;dxdz=cosβdS,dydz=cosγdS; 而α,β,γ的余弦是可以通过法向量的数量积求得的,所以可以写成: ∫∫P(x,y,z)dxdy+Q(x,y,z)dydz+R(x,y,z)dxdz=∫∫[P(x,y,z)cosα+Q(x,y,z)cosγ+R(x,y,z)cosβ]dS 在向各个坐标平面投影的时候需要注意dS的有向性,即夹角的大小,在夹角大于π/2的时候,其余弦值是负的。曲面积分http://v.youku.com/v_show/id_XMTY1NzQwNzY4.html
曲面应满足什么条件才能使高斯公式成立?曲面应是分片光滑的闭曲面!!!
Gauss公式的实质
表达了空间闭区域上的三重积分与其边界曲面上的曲面积分之间的关系.
物理意义----通量与散度
向量场
曲线积分和曲面积分的物理意义是什么啊?
变力做功的问题就是一个典型的曲线积分问题。
电通量和磁通量问题就是一个典型的曲面积分问题。
对于矢量而言,
闭合曲线积分:环流;
闭合曲面积分:通量。
闭合曲线上的斯托克斯积分,揭示了什么样的物理现象?
有旋还是无旋
高斯散度定理
更加精确地说,高斯公式说明向量场穿过曲面的通量,等于曲面内部区域的散度的三重积分。直观地,所有源点的和减去所有汇点的和,就是流出一个区域的流量。
高斯公式在工程数学中是一个很重要的结果,特别是静电学和流体力学。
定理
设空间闭区域Ω是由分片光滑的闭曲面Σ所围成,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在Ω上具有一阶连续偏导数,则有这两个公式叫做高斯公式。
用散度表示
高斯公式用散度表示为:用向量表示
令V代表有一间单闭曲面S为边界的体积, 是定义在V中和S上连续可微的矢量场。如果
是定义在V中和S上连续可微的矢量场。如果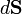 是外法向矢量面元,则
是外法向矢量面元,则推论
- 对于标量函数g和向量场F的积,应用高斯公式可得:
- 对于两个向量场
 的向量积,应用高斯公式可得:
的向量积,应用高斯公式可得:
- 对于标量函数f和非零常向量的积,应用高斯公式可得:
- 对于向量场F和非零常向量的向量积,应用高斯公式可得:
例子
假设我们想要计算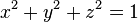 所定义的单位球,F是向量场
所定义的单位球,F是向量场 和
和 是奇函数,我们有:
是奇函数,我们有:二阶张量的高斯公式
二阶张量的高斯公式实际上是上面的高斯公式的推论。为了使内容完整,首先简要地介绍三维欧几里得空间上的二阶张量(详见并矢张量或张量积)以及相关的概念和记号。在这里,矢量和矢量场用黑斜体字母表示,张量用正黑体字母表示。- 两个矢量
 和
和 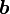 并排放在一起所形成的量
并排放在一起所形成的量  被称为矢量
被称为矢量  和
和 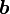 的并矢或并矢张量。要注意,一般来说,
的并矢或并矢张量。要注意,一般来说, 。
。
 的充分必要条件是
的充分必要条件是 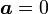 或
或  。
。
- 二阶张量就是有限个并矢的线性组合。
 分别线性地依赖于
分别线性地依赖于  和
和 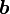 。
。
- 二阶张量
 和矢量
和矢量  的缩并
的缩并  以及
以及  对
对  和
和  都是线性的。
都是线性的。
- 特别是,当
 时,
时,
 。
。下面举一个例子:用二阶张量及其与矢量的缩并来重新写
 和
和 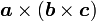 。
。 的转置
的转置  (又可以记为
(又可以记为  ),定义如下:
),定义如下: 仍然是一个二阶张量,并且线性地依赖于
仍然是一个二阶张量,并且线性地依赖于  。
。
 。
。
 是三维欧几里得空间中的一个有限区域,
是三维欧几里得空间中的一个有限区域, 是它的边界曲面,
是它的边界曲面,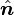 是
是  的外法线方向上的单位矢量,
的外法线方向上的单位矢量, 是定义在
是定义在  的某个开邻域上的
的某个开邻域上的  连续的二阶张量场,
连续的二阶张量场, 是
是  的转置,则
的转置,则 ,则
,则参阅
格林公式
在物理学与数学中,
格林定理连结了一个封闭曲线上的线积分与一个边界为 C 且平面区域为 D 的双重积分。格林定理是斯托克斯定理的二维特例,以英国数学家乔治·格林(George Green)命名。
设闭区域D由分段光滑的曲线 L 围成,函数 P(x,y)及 Q(x,y)在 D 上具有一阶连续偏导数,则有
此公式叫做格林公式,它给出了沿着闭曲线C的曲线积分与C所包围的区域D上的二重积分之间的关系。另见格林第一公式、格林第二公式。
如果我们可以证明
把右图中I型的区域D定义为:
对于C1,使用参数方程:x = x,y = g1(x),a ≤ x ≤ b。那么:
| 微积分学 | ||||||
 | ||||||
函数 · 导数 · 微分 · 积分
| ||||||
设闭区域D由分段光滑的曲线 L 围成,函数 P(x,y)及 Q(x,y)在 D 上具有一阶连续偏导数,则有
此公式叫做格林公式,它给出了沿着闭曲线C的曲线积分与C所包围的区域D上的二重积分之间的关系。另见格林第一公式、格林第二公式。
特殊情况的证明
以下是特殊情况下定理的一个证明,其中D是一种I型的区域,C2和C4是竖直的直线。对于II型的区域D,其中C1和C3是水平的直线。如果我们可以证明
把右图中I型的区域D定义为:
对于C1,使用参数方程:x = x,y = g1(x),a ≤ x ≤ b。那么:
参见
斯托克斯公式
 为边界的分片光滑的有向曲面,Γ 的正向与 S 的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面 S(连同边界 Γ)上具有一阶连续偏导数,则有
为边界的分片光滑的有向曲面,Γ 的正向与 S 的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面 S(连同边界 Γ)上具有一阶连续偏导数,则有
该定理的第一个已知的书面形式由威廉·汤姆森 (开尔文勋爵)给出,出现在他给斯托克斯的信中。
类似的,高斯散度定理
微积分基本定理和格林定理也是一般性斯托克斯定理的特例。
使用微分形式的一般化斯托克斯定理当然比其特例更强,虽然后者更直观而且经常被使用它的科学工作者或工程师认为更方便。
该定理经常用于 M 是嵌入到某个定义了 ω 的更大的流形中的子流形的情形。
定理可以简单的推广到分段光滑的子流形的线性组合上。斯托克斯定理表明相差一个恰当形式的闭形式在相差一个边界的链上的积分相同。这就是同调群和德拉姆上同调可以配对的基础。
利用斯托克斯公式可计算曲线积分。
ℝ³ 上的斯托克斯公式
设 Γ 为分段光滑的空间有向闭曲线,S 是以 为边界的分片光滑的有向曲面,Γ 的正向与 S 的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面 S(连同边界 Γ)上具有一阶连续偏导数,则有
为边界的分片光滑的有向曲面,Γ 的正向与 S 的侧符合右手规则,函数P(x,y,z)、Q(x,y,z)、R(x,y,z)在曲面 S(连同边界 Γ)上具有一阶连续偏导数,则有该定理的第一个已知的书面形式由威廉·汤姆森 (开尔文勋爵)给出,出现在他给斯托克斯的信中。
类似的,高斯散度定理
微积分基本定理和格林定理也是一般性斯托克斯定理的特例。
使用微分形式的一般化斯托克斯定理当然比其特例更强,虽然后者更直观而且经常被使用它的科学工作者或工程师认为更方便。
另一种形式
通过以下公式可以在对坐标的曲线积分和对面积的面积积分之间相互转换:流形上的斯托克斯公式
令 M 为一个可定向分段光滑 n 维流形,令 ω 为 M 上的 n−1 阶 C1 类紧支撑微分形式。如果 ∂M 表示 M 的边界,并以 M 的方向诱导的方向为边界的方向,则该定理经常用于 M 是嵌入到某个定义了 ω 的更大的流形中的子流形的情形。
定理可以简单的推广到分段光滑的子流形的线性组合上。斯托克斯定理表明相差一个恰当形式的闭形式在相差一个边界的链上的积分相同。这就是同调群和德拉姆上同调可以配对的基础。
应用
斯托克斯公式是格林公式的推广。利用斯托克斯公式可计算曲线积分。
(2012-06-14
15:27)
标签:
杂谈 |
离散元发展历程
离散元方法(DEM)首次于19世纪70年代由CundallandStrack在《A
discrete numerical model for granular
assemblies》一文提出,并不断得到学者的关注和发展。离散元在我国起步比较晚,但是发展迅速,1986年第一届全国岩石力学数值计算及模型试验讨论会上,王泳嘉首次向我国岩石力学与工程界介绍了离散元法的基本原理及几个应用例子。
离散元基本原理
离散元法是专门用来解决不连续介质问题的数值模拟方法。该方法把节理岩体视为由离散的岩块和岩块间的节理面所组成,允许岩块平移、转动和变形,而节理面可被压缩、分离或滑动。因此,岩体被看作一种不连续的离散介质。其内部可存在大位移、旋转和滑动乃至块体的分离,从而可以较真实地模拟节理岩体中的非线性大变形特征。离散元法的一般求解过程为:将求解空间离散为离散元单元阵,并根据实际问题用合理的连接元件将相邻两单元连接起来;单元间相对位移是基本变量,由力与相对位移的关系可得到两单元间法向和切向的作用力;对单元在各个方向上与其它单元间的作用力以及其它物理场对单元作用所引起的外力求合力和合力矩,根据牛顿运动第二定律可以求得单元的加速度;对其进行时间积分,进而得到单元的速度和位移。从而得到所有单元在任意时刻的速度、加速度、角速度、线位移和转角等物理量。
离散元应用领域
离散元技术在岩土、矿冶、农业、食品、化工、制药和环境等领域有广泛地应用,可分为分选、凝聚、混合、装填和压制、推铲、储运、粉碎、爆破、流态化等过程。颗粒离散元法在上述领域均有不少应用:料仓卸料过程的模拟;堆积、装填和压制;颗粒混合过程的模拟。
相关计算机软件
目前开发离散元商用程序最有名的公司要属由离散元思想首创者Cundall加盟的ITASCA国际工程咨询公司.该公司开发的二维UDEC(universal
distinct element code)和三维3DEC(3-dimensional distinct
elementcode)块体离散元程序,主要用于模拟节理岩石或离散块体岩石在准静或动载条件下力学过程及采矿过程的工程问题.该公司开发的PFC2D和PFC3D(particle
flow code in 2/3
dimensions)则分别为基于二维圆盘单元和三维圆球单元的离散元程序.它主要用于模拟大量颗粒元的非线性相互作用下的总体流动和材料的混合,含破损累计导致的破裂、动态破坏和地震响应等问题.Thornton的研究组研制了GRANULE程序,可进行包括不同形状的干、湿颗粒结块的碰撞一破裂规律研究,离散本构关系的细观力学分析,料仓料斗卸料规律研究等.国内离散元软件的开发相对还比较落后,但随着离散元方法研究在国内的升温,也出现了用于土木工程设计的块体离散元分析系统2D—Block[oJ和三维离散单元法软件TRUDEC及应用,以及北京大学刘凯欣研究小组开发的基于二维圆盘单元和三维球单元为基础的SUPER-DEM离散元力学分析系统。
最近,中国科学院非连续介质力学与工程灾害联合实验室与极道成然科技有限公司联合开发了国内最新的离散元大型商用软件GDEM,该软件基于中科院力学所非连续介质力学与工程灾害联合实验室开发的CDEM算法,将有限元与块体离散元进行有机结合,并利用GPU加速技术,可以高效的计算从连续到非连续整个过程。GDEM软件拥有完全独立的自主知识产权,代表了离散元的最高发展水平,让国人和世界站在了同一起跑线上。
参考文献:
A GPU Accelerated
Continuous-based Discrete Element Method for Elastodynamics Analysis.
基于CDEM的高桩码头承载力数值模拟
离散元法及其在岩土工程中的应用综述
颗粒流的离散元法模拟及其进展
离散元法研究的评述
离散元的历史
离散元(discrete element method, distinct element method)是一种数值计算方法,主要用来计算大量颗粒在给定条件下如何运动。1971年Cundall提出此方法时采用ditinct element method是为了和连续介质力学中的finite element method相区别。后来用discrete element method取代了distinct element method,以反映系统是离散的之一本质特征。1971年Cundall提出适于岩石力学的离散元法, 1979年Cundall和Strack又提出适于土力学的离散元法,并推出二维圆盘(disc)程序BALL和三维圆球程序TRUBAL(后发展成商业软件PFC-2D/3D),形成较系统的模型与方法,被称为软颗粒模型;
离散元与分子动力学的比较
从本质上来讲,离散元和分子动力学方法类似(molecular dynamics),以至于有些作者在文献中不加区别的使用MD和DEM两个名字。然而离散元和分子动力学相似性只体现在形式上的相似(颗粒和牛顿定理)。二者还是有很大差别,在于分子动力学计算原子如何在给定相互作用势下如何运动,而离散元计算的颗粒通常为微米及毫米量级。此外,离散元方法中需要考虑颗粒体在外力作用下的旋转运动,颗粒的形状,颗粒尺寸分布,以及颗粒之间填充气体,液体对颗粒材料宏观性能都有很大的影响。总之,即使计算模拟一个最简单的颗粒系统,单一尺寸的球形颗粒考虑摩擦作用下的运动问题都涉及到许多需要仔细考虑的细节,然而正如其他模拟方法一样,这些细节往往不会被作者在文章中出版,大多靠自己在实践中去不断领悟。计算流程
第一步:建立所需要的几何模型并产生颗粒。几何模型可以根据实际计算模型需要建立,颗粒产生通常为随机产生,及在给定的几何空间内随机产生所需要的颗粒。产生颗粒时需要实时监测新产生的颗粒和已有颗粒之间的位置关系,任意两颗粒之间不能有重叠,否则颗粒之间相互作用力可能很大而导致系统崩溃。所以如果几何模型尺寸,颗粒尺寸以及颗粒数目之间关系不合适,有可能导致颗粒产生失败。颗粒的初始速度需要根据模拟需要而给定。
第二步:确定接触模型。
接触模型是离散元计算的核心。所谓接触模型就是确定颗粒接触时的相互作用力。离散元计算中首先把相互作用力分解为法向力和切向力(法向指的是两接触颗粒中心之间的连线),所以接触模型一般包含法向相互作用和切向相互作用。
中文名称:离散元法英文名称:distinct element method
定义:由康德尔建立的应用于不连续岩体的数值求解方法。即将含不连续面的岩体看作若干块刚体组成,块体之间靠角点作用力维持平衡。角点接触力用弹簧和黏性元件描述,并服从牛顿第二定律。块体的位移和转动根据牛顿定律用动力松弛法按时步进行迭代求解。
应用学科:水利科技(一级学科);岩石力学、土力学、岩土工程(二级学科);岩石力学(水利)(三级学科)
离散元法(distinct element method,dem)是由cundall[1]提出的1种处理非连续介质问题的数值模拟方法,其理论基础是结合不同本构关系的牛顿第二定律,采用动态松弛法求解方程.
dem自问世以来,其主要应用领域集中在岩体工程和粉体(颗粒散体)工程.首先,在岩体计算力学方面,由于离散单元能更真实地表达节理岩体的几何特点,便于处理所有非线性变形和破坏都集中在节理面上的岩体破坏问题,被广泛应用于模拟边坡、滑坡和节理岩体地下水渗流等力学过程.其次,在粉体工程方面,颗粒离散元被广泛应用于粉体在复杂物理场作用下的复杂动力学行为的研究和多相混合材料介质或具有复杂结构的材料力学特性研究中.它涉及到粉末加工、研磨技术、混合搅拌等工业加工领域以及粮食等颗粒离散体的仓储和运输等生产实际领域.
岩体工程中的dem与颗粒dem并无本质不同,但在接触处理以及一些概念的认识上有一定区别.例如,在节理岩体问题中,单元之间总是处于相互接触或存在接触—断开的过程,均可视为准静态情况,在此基础上引入动态松弛法[2]将该准静态问题化为动力学问题进行求解.动态松弛法要求选取合适的阻尼,使函数收敛于静态值.在颗粒体问题中,颗粒间并不一定总存在接触,颗粒体间的相互碰撞也表现为动态的过程,此时采用动态松弛法进行求解并非为了得到静态值,而是为了引入阻尼系数以提供耗能装置,达到最大程度的模拟效果.
本文旨在对颗粒dem中阻尼等计算参数的选取方法进行阐述,有关dem原理的详细论述可参考文献[3].
1阻尼系数选取
颗粒dem中阻尼系数的选取可参考连续介质中阻尼的取法,引入工程中的黏性阻尼概念,采用rayleigh线性比例阻尼.rayleigh线性比例阻尼可以表示为
常用的系统振动阻尼比ζ的确定方法有半功率法和对数减量法等.
如前所述,rayleigh阻尼理论适用于连续介质系统,不完全适用于颗粒体这样的非连续介质系统,因为非连续介质系统随着单元之间的滑移或分离,其振型不确定,但阻尼却仍然存在,并可以用图1所示的物理模型解释.可以想象图中质量阻尼dm为把整个系统浸泡在黏性液体中,在物理意义上等价于用黏性活塞将颗粒单元与一不动点相连,使块体单元的绝对运动受到阻尼.刚度阻尼ds在物理意义上等价于用黏性活塞把两个接触块体相连,使颗粒单元之间的相对运动受到阻尼.
当颗粒之间接触完全脱离,即不存在颗粒之间的相互接触时,阻尼不再存在,或者将此时的阻尼理解为颗粒在空气中受到的质量阻尼.所以,在颗粒dem中,实际存在一个变阻尼的概念,包含至少两套阻尼,即接触时的质量阻尼加刚度阻尼和无接触时的空气质量阻尼.
对于连续介质来说,其振型、最小圆频率ωmin和最小临界阻尼系数ξmin等能够经过计算与实验得到.但是,对于非连续介质,由于其振型不确定,只能用试算的办法确定这些参数进而计算阻尼系数.颗粒dem中引入阻尼系数是为了提供耗能装置,并非为了得到准静态解,因此,阻尼系数的选取具有一定的灵活性,以满足最大程度模拟为原则.
2刚度系数选取
对刚度系数的考虑见图2,颗粒体a与颗粒体b存在两个角边接触,接触力分别为f1和f2,对于块体a有平衡方程
3时步选取
时步计算的理论基础是求解单自由度有阻尼弹性体系的中心差分格式下的临界时步δt.对于动力方程
由推导可知,采用上述方法计算的时步能够达到足够小,可以保证颗粒之间的接触过程得到充分模拟,不会出现这个时步颗粒之间刚刚开始接触,下个时步颗粒间的接触就反弹开了的现象,保证了接触模拟的真实性.
4算例
下面给出采用本文作者编制的颗粒dem筒仓计算程序sisolv-2[4],对某大型筒仓的装、卸料过程进行模拟的算例.对原60 m直径、20 m仓高的筒仓按25∶3缩小建立模型,模型尺寸见图3.模拟中采用的计算参数见表1.
5讨论
颗粒dem看似简单,其实却很难.如何选取上述几个参数对于初学者是很棘手的问题.要得到正确的模拟结果,需要在深入理解某些相关概念的基础上通过试算得到阻尼等计算参数,只有选取合理的计算参数才能保证模拟的真实性.
Discrete element method
A discrete
element method (DEM), also called a distinct element method is any of
family of numerical methods for computing the
motion of a large number of particles of micrometre-scale size and above. Though
DEM is very closely related to molecular
dynamics,
the method is generally distinguished by its inclusion of rotational
degrees-of-freedom as well as stateful contact and often complicated geometries
(including polyhedra). With advances in computing power and numerical algorithms
for nearest neighbor sorting, it has become possible to numerically simulate
millions of particles on a single processor. Today DEM is becoming widely
accepted as an effective method of addressing engineering problems in granular
and discontinuous materials, especially in granular flows, powder mechanics, and
rock mechanics.
Discrete element methods are relatively computationally intensive, which limits either the length of a simulation or the number of particles. Several DEM codes, as do molecular dynamics codes, take advantage of parallel processing capabilities (shared or distributed systems) to scale up the number of particles or length of the simulation. An alternative to treating all particles separately is to average the physics across many particles and thereby treat the material as a continuum. In the case of solid-like granular behavior as in soil mechanics, the continuum approach usually treats the material as elastic or elasto-plastic and models it with the finite element method or a mesh free method. In the case of liquid-like or gas-like granular flow, the continuum approach may treat the material as a fluid and use computational fluid dynamics. Drawbacks to homogenization of the granular scale physics, however, are well-documented and should be considered carefully before attempting to use a continuum approach.
The following forces may have to be considered in macroscopic simulations:
Typical integration methods used in a discrete element method are:
However, simulations in molecular dynamics divide the space in which the simulation take place into cells. Particles leaving through one side of a cell are simply inserted at the other side (periodic boundary conditions); the same goes for the forces. The force is no longer taken into account after the so-called cut-off distance (usually half the length of a cell), so that a particle is not influenced by the mirror image of the same particle in the other side of the cell. One can now increase the number of particles by simply copying the cells.
Algorithms to deal with long-range force include:
Discrete element methods are relatively computationally intensive, which limits either the length of a simulation or the number of particles. Several DEM codes, as do molecular dynamics codes, take advantage of parallel processing capabilities (shared or distributed systems) to scale up the number of particles or length of the simulation. An alternative to treating all particles separately is to average the physics across many particles and thereby treat the material as a continuum. In the case of solid-like granular behavior as in soil mechanics, the continuum approach usually treats the material as elastic or elasto-plastic and models it with the finite element method or a mesh free method. In the case of liquid-like or gas-like granular flow, the continuum approach may treat the material as a fluid and use computational fluid dynamics. Drawbacks to homogenization of the granular scale physics, however, are well-documented and should be considered carefully before attempting to use a continuum approach.
|
|
The DEM family
The various branches of the DEM family are the distinct element method proposed by Cundall in 1971, the generalized discrete element method proposed by Hocking, Williams and Mustoe in 1985, the discontinuous deformation analysis (DDA) proposed by Shi in 1988 and the finite-discrete element method concurrently developed by several groups (e.g., Munjiza and Owen). The general method was originally developed by Cundall in 1971 to problems in rock mechanics. The theoretical basis of the method was established by Sir Isaac Newton in 1697. Williams, Hocking, and Mustoe in 1985 showed that DEM could be viewed as a generalized finite element method. Its application to geomechanics problems is described in the book Numerical Modeling in Rock Mechanics, by Pande, G., Beer, G. and Williams, J.R.. The 1st, 2nd and 3rd International Conferences on Discrete Element Methods have been a common point for researchers to publish advances in the method and its applications. Journal articles reviewing the state of the art have been published by Williams, Bicanic, and Bobet et al. (see below). A comprehensive treatment of the combined Finite Element-Discrete Element Method is contained in the book The Combined Finite-Discrete Element Method by Munjiza.Applications
The fundamental assumption of the method is that the material consists of separate, discrete particles. These particles may have different shapes and properties. Some examples are:- liquids and solutions, for instance of sugar or proteins;
- bulk materials in storage silos, like cereal;
- granular matter, like sand;
- powders, like toner.
- Blocky or jointed rock masses
- Agriculture and food handling
- Chemical
- Civil Engineering
- Oil and gas
- Mining
- Mineral processing
- Pharmaceutical
- Powder metallurgy
Outline of the method
A DEM-simulation is started by first generating a model, which results in spatially orienting all particles and assigning an initial velocity. The forces which act on each particle are computed from the initial data and the relevant physical laws and contact models. Generally, a simulation consists of three parts: the initialization, explicit time-stepping, and post-processing. The time-stepping usually requires a nearest neighbor sorting step to reduce the number of possible contact pairs and decrease the computational requirements; this is often only performed periodically.The following forces may have to be considered in macroscopic simulations:
- friction, when two particles touch each other;
- contact plasticity, or recoil, when two particles collide;
- gravity, the force of attraction between particles due to their mass, which is only relevant in astronomical simulations.
- attractive potentials, such as cohesion, adhesion, liquid bridging, electrostatic attraction. Note that, because of the overhead from determining nearest neighbor pairs, exact resolution of long-range, compared with particle size, forces can increase computational cost or require specialized algorithms to resolve these interactions.
- the Coulomb force, the electrostatic attraction or repulsion of particles carrying electric charge;
- Pauli repulsion, when two atoms approach each other closely;
- van der Waals force.
Typical integration methods used in a discrete element method are:
Long-range forces
When long-range forces (typically gravity or the Coulomb force) are taken into account, then the interaction between each pair of particles needs to be computed. The number of interactions, and with it the cost of the computation, increases quadratically with the number of particles. This is not acceptable for simulations with large number of particles. A possible way to avoid this problem is to combine some particles, which are far away from the particle under consideration, into one pseudoparticle. Consider as an example the interaction between a star and a distant galaxy: The error arising from combining all the stars in the distant galaxy into one point mass is negligible. So-called tree algorithms are used to decide which particles can be combined into one pseudoparticle. These algorithms arrange all particles in a tree, a quadtree in the two-dimensional case and an octree in the three-dimensional case.However, simulations in molecular dynamics divide the space in which the simulation take place into cells. Particles leaving through one side of a cell are simply inserted at the other side (periodic boundary conditions); the same goes for the forces. The force is no longer taken into account after the so-called cut-off distance (usually half the length of a cell), so that a particle is not influenced by the mirror image of the same particle in the other side of the cell. One can now increase the number of particles by simply copying the cells.
Algorithms to deal with long-range force include:
Combined finite-discrete element method
Following the work by Munjiza and Owen's earlier work, the combined-discrete element method has been further developed to various irregular and deformable particles in many applications including pharmaceutical tableting,[1] packaging and flow simulations,[2] and concrete and impact analysis,[3] and many other applications.Advantages and limitations
Advantages- DEM can be used to simulate a wide variety of granular flow and rock mechanics situations. Several research groups have independently developed simulation software that agrees well with experimental findings in a wide range of engineering applications, including adhesive powders, granular flow, and jointed rock masses.
- DEM allows a more detailed study of the micro-dynamics of powder flows than is often possible using physical experiments. For example, the force networks formed in a granular media can be visualized using DEM. Such measurements are nearly impossible in experiments with small and many particles.
- The maximum number of particles, and duration of a virtual simulation is limited by computational power. Typical flows contain billions of particles, but contemporary DEM simulations on large cluster computing resources have only recently been able to approach this scale for sufficiently long time (simulated time, not actual program execution time).
References
- ^ R W Lewis, D T Gethin, X-S Yang, R. Rowe, A Combined Finite-Discrete Element Method for Simulating Pharmaceutical Powder Tableting, Int. J. Num. Method in Engineering, 62, 853–869 (2005)
- ^ D T Gethin, X-S Yang and R W Lewis; A Two Dimensional Combined Discrete and Finite Element Scheme for Simulating the Flow and Compaction of Systems Comprising Irregular Particulates, Computer Methods in Applied Mechanics and Engineering, 195, 2006, 5552–5565 (2006)
- ^ I. M. May, Y. Chen, D. R. J. Owen, Y.T. Feng and P. J. Thiele: Reinforced concrete beams under drop-weight impact loads, Computers and Concrete, 3 (2–3): 79–90 (2006).
Bibliography
Book- Ante Munjiza, The Combined Finite-Discrete Element Method Wiley, 2004, ISBN 0-470-84199-0
- Bicanic, Ninad, Discrete Element Methods in Stein, de Borst, Hughes Encyclopedia of Computational Mechanics, Vol. 1. Wiley, 2004. ISBN 0-470-84699-2.
- Griebel, Knapek, Zumbusch, Caglar: Numerische Simulation in der Molekulardynamik. Springer, 2004. ISBN 3-540-41856-3.
- Williams, J.R., Hocking, G., and Mustoe, G.G.W., “The Theoretical Basis of the Discrete Element Method,” NUMETA 1985, Numerical Methods of Engineering, Theory and Applications, A.A. Balkema, Rotterdam, January 1985
- Pande, G., Beer, G. and Williams, J.R., Numerical Modeling in Rock Mechanics, John Wiley and Sons, 1990.
- Farhang Radjaï and Frédéric Dubois, "Discrete-element Modeling of Granular Materials", Wiley, 2011, ISBN 978-1-84821-260-2
- Thorsten Pöschel and Thomas Schwager, Computational Granular Dynamics, models and algorithms. Springer, 2005. ISBN 3-540-21485-2.
- A. Bobet, A. Fakhimi, S. Johnson, J. Morris, F. Tonon, and M. Ronald Yeung (2009) "Numerical Models in Discontinuous Media: Review of Advances for Rock Mechanics Applications", J. Geotech. and Geoenvir. Engrg., 135 (11) pp. 1547–1561
- P.A. Cundall, O.D.L. Strack, A discrete numerical model for granular assemblies. Geotechnique, 29:47–65, 1979.
- Kawaguchi, T., Tanaka, T. and Tsuji, Y., Numerical simulation of two-dimensional fluidized beds using the discrete element method (comparison between the two- and three-dimensional models) Powder Technology, 96(2):129–138, 1998.
- Williams, J.R. and O’Connor, R., Discrete Element Simulation and the Contact Problem, Archives of Computational Methods in Engineering, Vol. 6, 4, 279–304, 1999
- Zhu HP, Zhou ZY, Yang RY, Yu AB. Discrete particle simulation of particulate systems: Theoretical developments. Chemical Engineering Science. 2007;62:3378-3396
- Zhu HP, Zhou ZY, Yang RY, Yu AB. Discrete particle simulation of particulate systems: A review of mayor applications and findings. Chemical Engineering Science. 2008;63:5728-5770.
- Shi, G, Discontinuous deformation analysis – A new numerical model for the statics and dynamics of deformable block structures, 16pp. In 1st U.S. Conf. on Discrete Element Methods, Golden. CSM Press: Golden, CO, 1989.
- Williams, J.R. and Pentland, A.P., "Superquadric and Modal Dynamics for Discrete Elements in Concurrent Design," National Science Foundation Sponsored 1st U.S. Conference of Discrete Element Methods, Golden, CO, October 19–20, 1989.
- 2nd International Conference on Discrete Element Methods, Editors Williams, J.R. and Mustoe, G.G.W., IESL Press, 1992 ISBN 0-918062-88-8
Software
Open source and non-commercial software:- Ascalaph Molecular dynamics with fourth order symplectic integrator.
- BALL & TRUBAL (1979–1980) distinct element method (FORTRAN code), originally written by P.Cundall and currently maintained by Colin Thornton.
- dp3D (discrete powder 3D), DEM code oriented toward material science engineering applications (powder compaction, powder sintering, fracture of brittle materials...). Emphasis is put on the physics of the contact laws. dp3D is written in fortran 90 and heavily parallelised with OpenMP.
- ESyS-Particle ESyS-Particle is a high-performance computing implementation of the Discrete Element Method released under the Open Software License v3.0. To date, development focus is on geoscientific applications including granular flow, rock breakage and earthquake nucleation. ESyS-Particle includes a Python scripting interface providing flexibility for simulation setup and real-time data analysis. The DEM computing engine is written in C++ and parallelised using MPI, permitting simulations of more than 1 million particles on clusters or high-end workstations.
- LAMMPS is a very fast parallel open-source molecular dynamics package with GPU support also allowing DEM simulations. LAMMPS Website, Examples .
- LIGGGHTS is a code based on LAMMPS with more DEM features such as wall import from CAD, a moving mesh feature and granular heat transfer. Further a coupling to CFD is available. LIGGGHTS Website
- SDEC Spherical Discrete Element Code.
- LMGC90 Open platform for modelling interaction problems between elements including multi-physics aspects based on an hybrid or extended FEM – DEM discretization, using various numerical strategies as MD or NSCD.
- Pasimodo PASIMODO is a program package for particle-based simulation methods. The main field of application is the simulation of granular media, such as sand, gravel, granulates in chemical engineering and others. Moreover it can be used for the simulation of many other Lagrangian methods, e.g. fluid simulation with Smoothed-Particle-Hydrodynamics.
- Yade Yet Another Dynamic Engine (historically related to SDEC), modular and extensible toolkit of DEM algorithms written in c++. Tight integration with Python gives flexibility to simulation description, real-time control and post-processing, and allows introspection of all internal data. Can run in parallel on shared-memory machines using OpenMP.
- MechSys Although it is initially a package dedicated to the FEM method, it also contains a DEM module. It uses both spherical elements and spheropolyhedra to model collision of particles with general shapes. Both elastic and cohesive forces are included to model damage and fracture processes. Parallelization is achieved mostly by the new std::thread library of the new C++ standard. There is also a module dealing with the coupling between DEM and LBM still under development.
- Bulk Flow Analyst (Applied DEM) General-purpose 3D DEM tool for mechanical engineering applications. Imports many types of 3D modelling files (including DXF, IGES, and STEP) and integrates with AutoCAD and SolidWorks as well as providing its own 3D interface.
- Chute Analyst (Overland Conveyor Company) 3D DEM tool for transfer chute engineering applications. Imports many types of 3D modelling files (including DXF, IGES, and STEP) and integrates with AutoCAD and SolidWorks as well as providing its own 3D interface.
- Chute Maven (Hustrulid Technologies Inc.) Spherical Discrete Element Modeling in 3 Dimensions. Directly reads in AutoCad dxf files and interfaces with SolidWorks.
- EDEM (DEM Solutions Ltd.) General-purpose DEM simulation with CAD import of particle and machine geometry, GUI-based model set-up, extensive post-processing tools, progammable API, couples with CFD, FEA and MBD software.
- ELFEN
- GROMOS 96
- MIMES a variety of particle shapes can be used in 2D
- PASSAGE/DEM (PASSAGE/DEM Software is for predicting the flow particles under a wide variety of forces.)
- PFC (2D & 3D) Particle Flow Code.
- SimPARTIX DEM and SPH simulation package from Fraunhofer IWM
- StarCCM+ Engineering analysis suite for solving problems involving flow (of fluids or solids), heat transfer and stress.
- UDEC and 3DEC Two- and three-dimensional simulation of the response of discontinuous media (such as jointed rock) that is subject to either static or dynamic loading.
- DEMpack Discrete / finite element simulation software in 2D and 3D, user interface based on GiD.
- MFIX
See also
http://wenku.baidu.com/view/678738d380eb6294dd886c90
http://wenku.baidu.com/view/112dbf0e76c66137ee0619da
http://wenku.baidu.com/view/e38ca5d5360cba1aa811dafb
离散元方法与有限元方法的比较http://www.docin.com/p-99509567.html
标签:
杂谈 |
整体微分几何(Global Differential Geometry)
微分几何
微分几何研究微分流形的几何性质,是现代数学中一主流;是广义相对论的基础,与拓扑学、代数几何及理论物理关系密切。
古典微分几何起源于微积分,主要内容为曲线论和曲面论。欧拉、蒙日和高斯被公认为古典微分几何的奠基人。近代微分几何的创始人是黎曼,他在1854年创立了黎曼几何(实际上黎曼提出的是芬斯勒几何),这成为近代微分几何的主要内容,并在相对论有极为重要的作用。埃利·嘉当和陈省身等人曾在微分几何领域做出极为杰出的贡献。
内在的观点更加灵活,例如在相对论中时空不能很自然的用外在形式表示。但用内在的观点,曲率和联络这样的结构比较难定义一些,所以采用内在的观点也不是没有代价的。
这两种观点也是可以融通的,即外在几何可以被看作是附加于内在几何上的结构。(见纳什嵌入定理)
可微流形是一个拓扑空间,它有一个开覆盖,其中的每个开集同胚于Rn中的一个开单位球。并且,如果f,g是其中两个同胚映射,则函数 无限可微。我们称一个函数无限可微,如果它和每个同胚的复合是从开球到R的无限可微函数。
无限可微。我们称一个函数无限可微,如果它和每个同胚的复合是从开球到R的无限可微函数。
在流形的每一点,有一个该点的切空间,它由每个从该点离开进行运动的所有可能的速度(方向和大小)所组成。对一个n维流形,每点的切空间是一个n维向量空间,或者说是一个Rn。切空间有多种定义。其中一个是作为所有在该点取值为0的函数组成的线性空间的对偶空间,除以所有取值为0 并且一阶导数为0的函数空间(所得到的余空间)。导数为0可以定义为“和任何可微的从实数到该流形的函数的复合的导数为0”,因而只需要用到可微性。
向量场是从流形到它的切空间的并集(切丛)的函数,在每一点所取的值是该点的切空间的一个元素。这样的映射称为纤维丛的截面。向量场可微,如果该向量场应用到每个可微函数都得到一个可微函数。向量场可以看作是时不变的微分方程组。从实数到流形的可微函数是流形上的曲线。这给了一个从实数到切空间的函数:曲线上每点的速度。一条曲线称为一个向量场的一个解,如果曲线每点的速度和向量场在该点的值相等。
交错k维线性形式是向量空间V的对偶空间V*的反对称k阶向量积的一个元素。k微分形式就是在流形的每一点选取一个这样的交错k形式--V在这里就是该点的切空间。如果它作用在k个可微向量场上的结果是流形上的一个可微
分支
黎曼几何以黎曼流形为主要研究对象— 有额外结构的光滑流形,他们因此无穷小得看起来像欧几里得空间。这使得欧几里得几何的诸如函数的梯度,散度,曲线的长度等概念得到了推广;而无须假设空间整体上有这么对称。
研究的对象是复流形。这是一类有着可积的近复结构的微分流形。因为非奇异的复代数簇自然的是复流形,因此与复代数几何有着紧密的联系。
这是研究辛流形的学科。一个辛流形是带有辛形式(也就是,一个闭的非退化2-形式)的微分流形。
这是辛几何在奇数维上的对应物。大致来说,在(2n+1)微流形上的切触结构是一个1-形式α使得 处处非退化。
处处非退化。
芬斯勒几何以芬斯勒流形为主要研究对象— 这是一个有芬斯勒度量的微分流形,也就是切空间被赋予了巴拿赫范数。芬斯勒度量是比黎曼度量一般得多的结构。
Richard Palais's 3DXM Surfaces Gallery
2. Manfredo Do Carmo (1976), Differential Geometry of Curves and Surfaces. Prentice Hall.
3. Manfredo Perdigao do Carmo, Francis Flaherty (1994), Riemannian Geometry.
4. John McCleary (1994), Geometry from a Differentiable Viewpoint
5. Ethan D. Bloch (1996), A First Course in Geometric Topology and Differential Geometry
6. Alfred Gray (1998), Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed.
古典微分几何起源于微积分,主要内容为曲线论和曲面论。欧拉、蒙日和高斯被公认为古典微分几何的奠基人。近代微分几何的创始人是黎曼,他在1854年创立了黎曼几何(实际上黎曼提出的是芬斯勒几何),这成为近代微分几何的主要内容,并在相对论有极为重要的作用。埃利·嘉当和陈省身等人曾在微分几何领域做出极为杰出的贡献。
内在对外在
从一开始到19世纪中叶,微分几何是从外在观点来进行研究的:曲线和曲面是被放在更高维欧几里得空间中来考虑的(譬如曲面被放在三维的背景空间中)。其中的最简单的成果就是曲线微分几何中的结果。内在观点开始于黎曼的工作,在那里因为几何对象被认为是独立的给出的,所以不能说移到外面来考虑这个对象。内在的观点更加灵活,例如在相对论中时空不能很自然的用外在形式表示。但用内在的观点,曲率和联络这样的结构比较难定义一些,所以采用内在的观点也不是没有代价的。
这两种观点也是可以融通的,即外在几何可以被看作是附加于内在几何上的结构。(见纳什嵌入定理)
技术要求
微分几何的工具也就是流形上的微积分:包括对于流形,切丛,余切丛,微分形式,外微分,p-形式在p维子流形上的积分以及斯托克斯定理,楔积,和李导数的研究。这些都和多变量微积分相关;但对于几何上的应用来讲,必须发展一种在某种意义上和特定坐标系无关的方法。微分几何的特殊概念可以说是那些体现几何本质的二阶导数:曲率的很多表现方式。可微流形是一个拓扑空间,它有一个开覆盖,其中的每个开集同胚于Rn中的一个开单位球。并且,如果f,g是其中两个同胚映射,则函数
 无限可微。我们称一个函数无限可微,如果它和每个同胚的复合是从开球到R的无限可微函数。
无限可微。我们称一个函数无限可微,如果它和每个同胚的复合是从开球到R的无限可微函数。在流形的每一点,有一个该点的切空间,它由每个从该点离开进行运动的所有可能的速度(方向和大小)所组成。对一个n维流形,每点的切空间是一个n维向量空间,或者说是一个Rn。切空间有多种定义。其中一个是作为所有在该点取值为0的函数组成的线性空间的对偶空间,除以所有取值为0 并且一阶导数为0的函数空间(所得到的余空间)。导数为0可以定义为“和任何可微的从实数到该流形的函数的复合的导数为0”,因而只需要用到可微性。
向量场是从流形到它的切空间的并集(切丛)的函数,在每一点所取的值是该点的切空间的一个元素。这样的映射称为纤维丛的截面。向量场可微,如果该向量场应用到每个可微函数都得到一个可微函数。向量场可以看作是时不变的微分方程组。从实数到流形的可微函数是流形上的曲线。这给了一个从实数到切空间的函数:曲线上每点的速度。一条曲线称为一个向量场的一个解,如果曲线每点的速度和向量场在该点的值相等。
交错k维线性形式是向量空间V的对偶空间V*的反对称k阶向量积的一个元素。k微分形式就是在流形的每一点选取一个这样的交错k形式--V在这里就是该点的切空间。如果它作用在k个可微向量场上的结果是流形上的一个可微
分支
黎曼几何以黎曼流形为主要研究对象— 有额外结构的光滑流形,他们因此无穷小得看起来像欧几里得空间。这使得欧几里得几何的诸如函数的梯度,散度,曲线的长度等概念得到了推广;而无须假设空间整体上有这么对称。
研究的对象是复流形。这是一类有着可积的近复结构的微分流形。因为非奇异的复代数簇自然的是复流形,因此与复代数几何有着紧密的联系。
这是研究辛流形的学科。一个辛流形是带有辛形式(也就是,一个闭的非退化2-形式)的微分流形。
这是辛几何在奇数维上的对应物。大致来说,在(2n+1)微流形上的切触结构是一个1-形式α使得
 处处非退化。
处处非退化。芬斯勒几何以芬斯勒流形为主要研究对象— 这是一个有芬斯勒度量的微分流形,也就是切空间被赋予了巴拿赫范数。芬斯勒度量是比黎曼度量一般得多的结构。
外部链接
A Modern Course on Curves and Surface, Richard S Palais, 2003Richard Palais's 3DXM Surfaces Gallery
参考书目
1. Michael Spivak (1999), A Comprehensive Introduction to Differential Geometry,(5 Volumes),3rd Edition.2. Manfredo Do Carmo (1976), Differential Geometry of Curves and Surfaces. Prentice Hall.
3. Manfredo Perdigao do Carmo, Francis Flaherty (1994), Riemannian Geometry.
4. John McCleary (1994), Geometry from a Differentiable Viewpoint
5. Ethan D. Bloch (1996), A First Course in Geometric Topology and Differential Geometry
6. Alfred Gray (1998), Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed.
Differential geometry

A triangle immersed in a
saddle-shape plane (a hyperbolic
paraboloid),
as well as two diverging ultraparallel
lines.
Differential
geometry is a mathematical discipline that uses the
techniques of differential
calculus and integral
calculus, as
well as linear
algebra and multilinear
algebra, to
study problems in geometry. The theory of plane and
space curves and of surfaces in the
three-dimensional Euclidean
space formed
the basis for development of differential geometry during the 18th
century and
the 19th
century.
Since the late 19th century, differential geometry has grown into a field
concerned more generally with the geometric structures on differentiable
manifolds.
Differential geometry is closely related to differential
topology,
and to the geometric aspects of the theory of differential
equations. Grigori
Perelman's
proof of the Poincaré
conjecture using the techniques
of Ricci
flows demonstrated the power of the
differential-geometric approach to questions in topology and it highlighted the
important role played by its analytic methods. The differential
geometry of surfaces captures many of the key
ideas and techniques characteristic of this field.
Branches of differential geometry
Riemannian geometry
Main
article: Riemannian
geometry
Riemannian geometry
studies Riemannian
manifolds, smooth
manifolds with a Riemannian
metric. This is a concept of distance expressed by means of a smooth positive
definite symmetric
bilinear form defined on the tangent space
at each point. Riemannian geometry generalizes Euclidean
geometry to
spaces that are not necessarily flat, although they still resemble the Euclidean
space at
each point "infinitesimally", i.e. in the first order of approximation. Various
concepts based on length, such as the arc
length of curves, area
of plane regions,
and volume of solids all possess natural
analogues in Riemannian geometry. The notion of a directional
derivative of a function from multivariable
calculus is
extended in Riemannian geometry to the notion of a covariant
derivative of a tensor. Many concepts and
techniques of analysis and differential equations have been generalized to the
setting of Riemannian manifolds.
A distance-preserving
diffeomorphism between Riemannian manifolds
is called an isometry. This notion can also be
defined locally, i.e. for small neighborhoods of points. Any two regular
curves are locally isometric. However, the Theorema
Egregium of Carl Friedrich
Gauss showed
that already for surfaces, the existence of a local isometry imposes strong
compatibility conditions on their metrics: the Gaussian
curvatures at the corresponding points
must be the same. In higher dimensions, the Riemann
curvature tensor is an important pointwise
invariant associated to a Riemannian manifold that measures how close it is to
being flat. An important class of Riemannian manifolds is the Riemannian
symmetric spaces, whose curvature is not
necessarily constant. These are the closest analogues to the "ordinary" plane
and space considered in Euclidean and non-Euclidean
geometry.
Pseudo-Riemannian geometry
Pseudo-Riemannian geometry generalizes Riemannian
geometry to the case in which the metric
tensor need
not be positive-definite. A special case of this is
a Lorentzian
manifold,
which is the mathematical basis of Einstein's general
relativity theory of gravity.
Finsler geometry
Finsler
geometry has
the Finsler manifold as the main object of study. This is a differential
manifold with a Finsler
metric, i.e.
a Banach
norm defined
on each tangent space. A Finsler metric is a much more general structure than a
Riemannian metric. A Finsler structure on a manifold M is a function
F
- F(x, my) = |m|F(x,y) for all x, y in TM,
- F is infinitely differentiable in TM − {0},
- The vertical Hessian of F2 is positive definite.
Symplectic geometry
Main
article: Symplectic
geometry
Symplectic
geometry is
the study of symplectic
manifolds.
An almost symplectic manifold is a differentiable manifold equipped with
a smoothly
varying non-degenerate skew-symmetric bilinear
form on each
tangent space, i.e., a nondegenerate 2-form
ω, called the
symplectic form. A symplectic manifold is an almost symplectic manifold
for which the symplectic form ω is closed: dω = 0.A diffeomorphism between two symplectic manifolds which preserves the symplectic form is called a symplectomorphism. Non-degenerate skew-symmetric bilinear forms can only exist on even dimensional vector spaces, so symplectic manifolds necessarily have even dimension. In dimension 2, a symplectic manifold is just a surface endowed with an area form and a symplectomorphism is an area-preserving diffeomorphism. The phase space of a mechanical system is a symplectic manifold and they made an implicit appearance already in the work of Joseph Louis Lagrange on analytical mechanics and later in Carl Gustav Jacobi's and William Rowan Hamilton's formulations of classical mechanics.
By contrast with Riemannian geometry, where the curvature provides a local invariant of Riemannian manifolds, Darboux's theorem states that all symplectic manifolds are locally isomorphic. The only invariants of a symplectic manifold are global in nature and topological aspects play a prominent role in symplectic geometry. The first result in symplectic topology is probably the Poincaré-Birkhoff theorem, conjectured by Henri Poincaré and then proved by G.D. Birkhoff in 1912. It claims that if an area preserving map of an annulus twists each boundary component in opposite directions, then the map has at least two fixed points.[1]
Contact geometry
Main
article: Contact
geometry
Contact
geometry deals with certain manifolds
of odd dimension. It is close to symplectic geometry and like the latter, it
originated in questions of classical mechanics. A contact structure on a
(2n + 1) - dimensional manifold M is given by a smooth hyperplane field
H in the tangent
bundle that
is as far as possible from being associated with the level sets of a
differentiable function on M (the technical term is "completely
nonintegrable tangent hyperplane distribution"). Near each point p, a
hyperplane distribution is determined by a nowhere vanishing 1-form  , which is unique up to multiplication by a nowhere vanishing
function:
, which is unique up to multiplication by a nowhere vanishing
function: then this form is contact if and only if the top-dimensional form
then this form is contact if and only if the top-dimensional formComplex and Kähler geometry
Complex differential geometry is the study of complex manifolds. An almost complex manifold is a real manifold , endowed with a tensor of type
(1 , 1), i.e. a
vector bundle
endomorphism (called an almost complex structure)
, endowed with a tensor of type
(1 , 1), i.e. a
vector bundle
endomorphism (called an almost complex structure) ,
such that
,
such that  .
.
An almost complex manifold is called complex if
 , where
, where  is a tensor of type (2 , 1) related to
is a tensor of type (2 , 1) related to  , called the Nijenhuis
tensor (or
sometimes the torsion). An almost complex manifold is complex if and only
if it admits a holomorphic coordinate
atlas. An
almost Hermitian structure is given by an almost
complex structure J, along with a Riemannian
metric g, satisfying the
compatibility condition
, called the Nijenhuis
tensor (or
sometimes the torsion). An almost complex manifold is complex if and only
if it admits a holomorphic coordinate
atlas. An
almost Hermitian structure is given by an almost
complex structure J, along with a Riemannian
metric g, satisfying the
compatibility condition .
.
 .
.
 is the Levi-Civita
connection of
is the Levi-Civita
connection of  . In this case,
. In this case,  is called a Kähler
structure, and a Kähler manifold is a manifold endowed
with a Kähler structure. In particular, a Kähler manifold is both a complex and
a symplectic
manifold. A
large class of Kähler manifolds (the class of Hodge
manifolds)
is given by all the smooth complex
projective varieties.
is called a Kähler
structure, and a Kähler manifold is a manifold endowed
with a Kähler structure. In particular, a Kähler manifold is both a complex and
a symplectic
manifold. A
large class of Kähler manifolds (the class of Hodge
manifolds)
is given by all the smooth complex
projective varieties.CR geometry
CR geometry is the study of the intrinsic geometry of boundaries of domains in complex manifolds.Differential topology
Differential topology is the study of (global) geometric invariants without a metric or symplectic form. It starts from the natural operations such as Lie derivative of natural vector bundles and de Rham differential of forms. Beside Lie algebroids, also Courant algebroids start playing a more important role.Lie groups
A Lie group is a group in the category of smooth manifolds. Beside the algebraic properties this enjoys also differential geometric properties. The most obvious construction is that of a Lie algebra which is the tangent space at the unit endowed with the Lie bracket between left-invariant vector fields. Beside the structure theory there is also the wide field of representation theory.Bundles and connections
The apparatus of vector bundles, principal bundles, and connections on bundles plays an extraordinarily important role in modern differential geometry. A smooth manifold always carries a natural vector bundle, the tangent bundle. Loosely speaking, this structure by itself is sufficient only for developing analysis on the manifold, while doing geometry requires, in addition, some way to relate the tangent spaces at different points, i.e. a notion of parallel transport. An important example is provided by affine connections. For a surface in R3, tangent planes at different points can be identified using a natural path-wise parallelism induced by the ambient Euclidean space, which has a well-known standard definition of metric and parallelism. In Riemannian geometry, the Levi-Civita connection serves a similar purpose. (The Levi-Civita connection defines path-wise parallelism in terms of a given arbitrary Riemannian metric on a manifold.) More generally, differential geometers consider spaces with a vector bundle and an arbitrary affine connection which is not defined in terms of a metric. In physics, the manifold may be the space-time continuum and the bundles and connections are related to various physical fields.Intrinsic versus extrinsic
From the beginning and through the middle of the 18th century, differential geometry was studied from the extrinsic point of view: curves and surfaces were considered as lying in a Euclidean space of higher dimension (for example a surface in an ambient space of three dimensions). The simplest results are those in the differential geometry of curves and differential geometry of surfaces. Starting with the work of Riemann, the intrinsic point of view was developed, in which one cannot speak of moving "outside" the geometric object because it is considered to be given in a free-standing way. The fundamental result here is Gauss's theorema egregium, to the effect that Gaussian curvature is an intrinsic invariant.The intrinsic point of view is more flexible. For example, it is useful in relativity where space-time cannot naturally be taken as extrinsic (what would be "outside" of it?). With the intrinsic point of view it is harder to define the central concept of curvature and other structures such as connections, so there is a price to pay.
These two points of view can be reconciled, i.e. the extrinsic geometry can be considered as a structure additional to the intrinsic one. (See the Nash embedding theorem.)
Applications of differential geometry
Below are some examples of how differential geometry is applied to other fields of science and mathematics.- In physics, three uses will be
mentioned:
- Differential geometry is the language in which Einstein's general theory of relativity is expressed. According to the theory, the universe is a smooth manifold equipped with a pseudo-Riemannian metric, which describes the curvature of space-time. Understanding this curvature is essential for the positioning of satellites into orbit around the earth. Differential geometry is also indispensable in the study of gravitational lensing and black holes.
- Differential forms are used in the study of electromagnetism.
- Differential geometry has applications to both Lagrangian mechanics and Hamiltonian mechanics. Symplectic manifolds in particular can be used to study Hamiltonian systems.
See also
- Integral geometry
- List of differential geometry topics
- Glossary of differential geometry and topology
- Important publications in differential geometry
- Important publications in differential topology
- Basic introduction to the mathematics of curved spacetime
- Affine differential geometry
- Projective differential geometry
- Noncommutative geometry
- Synthetic differential geometry
- Abstract differential geometry
- Discrete differential geometry
- Analysis on fractals
References
- ^ It is easy to show that the area preserving condition (or the twisting condition) cannot be removed. Note that if one tries to extend such a theorem to higher dimensions, one would probably guess that a volume preserving map of a certain type must have fixed points. This is false in dimensions greater than 3.
- ^ Paul Marriott and Mark Salmon (editors), "Applications of Differential Geometry to Econometrics", Cambridge University Press; 1 edition (September 18, 2000).
- ^ Jonathan H. Manton, "On the role of differential geometry in signal processing" [1].
- ^ Mario Micheli, "The Differential Geometry of Landmark Shape Manifolds: Metrics, Geodesics, and Curvature", http://www.math.ucla.edu/~micheli/PUBLICATIONS/micheli_phd.pdf
- ^ Anand A. Joshi, "Geometric methods for image processing and signal analysis", [2]
Further reading
- Wolfgang
Kühnel (2002). Differential Geometry: Curves - Surfaces - Manifolds (2nd
ed. ed.). ISBN
0-8218-3988-8. - Theodore
Frankel (2004). The geometry of physics: an introduction (2nd ed.
ed.). ISBN
0-521-53927-7. - Spivak, Michael (1999). A Comprehensive Introduction to Differential Geometry (5 Volumes) (3rd Edition ed.).
- do Carmo,
Manfredo (1976). Differential Geometry of Curves and Surfaces. ISBN
0-13-212589-7. Classical geometric approach to differential geometry without tensor analysis. - Kreyszig,
Erwin (1991). Differential Geometry. ISBN
0-486-66721-9. Good classical geometric approach to differential geometry with tensor machinery. - do Carmo, Manfredo Perdigao (1994). Riemannian Geometry.
- McCleary, John (1994). Geometry from a Differentiable Viewpoint.
- Bloch, Ethan D. (1996). A First Course in Geometric Topology and Differential Geometry.
- Gray, Alfred (1998). Modern Differential Geometry of Curves and Surfaces with Mathematica (2nd ed. ed.).
- Burke, William L. (1985). Applied Differential Geometry.
- ter Haar
Romeny, Bart M. (2003). Front-End Vision and Multi-Scale Image
Analysis. ISBN
1-4020-1507-0.
External links
- B. Conrad. Differential Geometry handouts, Stanford University
- Michael Murray's online differential geometry course, 1996
- A Modern Course on Curves and Surface, Richard S Palais, 2003
- Richard Palais's 3DXM Surfaces Gallery
- Balázs Csikós's Notes on Differential Geometry
- N. J. Hicks, Notes on Differential Geometry, Van Nostrand.
- MIT OpenCourseWare: Differential Geometry, Fall 2008
整体微分几何
课程名称:整体微分几何
预修要求:微分几何(局部理论)
内容简介:《整体微分几何》主要介绍曲线与曲面的大范围整体几何性质,包括某些拓扑性质。内容分四章:第一章介绍活动标架法,它是研究整体微分几何和几何分析的有力工具。第二章介绍3维欧氏空间中闭曲线的整体微分几何性质。第三章介绍3维欧氏空间中曲面的整体微分几何性质。第四章介绍曲面的内蕴几何。通过本课程学习,使学生掌握整体微分几何的基本概念和重要思想方法,了解数学各方向之间相互交织、相互渗透的现代数学概貌。
选用教材或参考书: 《整体微分几何初步》沈一兵编着
《整体微分几何》教学大纲
一、课程的教学目的和基本要求
主要内容:
(一)
1.
2.
3.
4.
(二)
1.
2.
(三)E3中曲面的整体微分几何
1.曲面的Gauss-Bonnet公式
2.球面的刚性定理 ▲
3.凸曲面与积分公式 ▲
4.全平均曲率与Willmore猜想 ▲
5.常负曲率曲面与Backlund变换 ▲
6.极小曲面的Bernstein定理
7.常平均曲率曲面
四、教材及主要参考书
教材:《整体微分几何初步》 沈一兵编著
主要参考书:(1)《微分几何》 苏步青、胡和生等编著
五、有关说明
书名:整体微分几何初步
著译者:沈一兵
出版日期:2005-10-01
出 版 社:浙江大学出版社
出版社: 浙江大学出版社; 第2版 (2005年10月1日)
丛书名: 新世纪高等院校精品教材
内容简介
原是作者学习整体微分几何和外形式法的一些心得体会,整理后于1998年由原杭州大学出版社出版,拟作数学系高年级本科生的选修课教材。出版后颇受广大读者重视和钟爱,不久书即告罄。书中不少内容源自著名几何学大师陈省身先生的学术论著和演讲。2001年先生来杭时曾对本书颇加嘉奖,并建议稍增内容,译成英文。但由于作者拖沓,一直未能兑现。不料先生于2004年12月3日突然仙逝,作者悲悼之余,也对此事遗憾万分。作者愿以再版此书敬献先生!本版与初版的主要差别是增加了第五章:高维欧氏空间的超曲面。这是三维欧氏空间中曲面论的最直接和最自然的推广,至今还在发展。
第一章 活动标架法.
1 幺正标架
1.1 幺正标架
1.2 幺正标架的运动方程
2 外微分形式
2.1 外代数
2.2 外微分形式
2.3 外微分
2.4 微分形式的积分
3 可积系统
3.1 E3的结构方程
3.2 Frobenius定理
3.3 用活动标架法研究曲面
3.3.1 第一和第二基本形式
3.3.2 主曲率、Gauss曲率和平均曲率
3.3.3 曲面论基本定理
第二章 曲线的整体微分几何
1 平面曲线的某些整体性质
1.1 等周不等式
1.2 曲线的旋转指标
.1.2.1 映射的度数
1.2.2 旋转指标定理
1.3 凸闭曲线
2 空间曲线的某些整体性质
2.1 球面上的Crofton公式
2.2 空间曲线的全曲率
2.3 空间曲线的全挠率
第三章 E3中曲面的整体微分几何
1 曲面的Gauss—Bonnet公式
1.1 曲面的整体描述
1.2 Gauss—Bonnet公式
2 Liebmann定理
2.1 球面的刚性
2.2 两个引理
2.3 Liebmann定理的证明
3 凸曲面和积分公式
3.1 凸曲面的Hadamard定理
3.2 Cohn—Vossen定理
3.3 Minkowski积分公式
4 Minkowski问题和Christoffel问题的唯一性
4.1 概述
4.2 基本公式
4.3 Minkowski问题的唯一性
4.4 Christoffel问题的唯一性
5 全平均曲率与Willmore猜想
5.1 全平均曲率
5.2 球面的一个特征
5.3 环面的全平均曲率
6 常负曲率曲面和Backlund变换
6.1 常负曲率曲面和SG方程
6.2 伪球线汇和焦曲面
6.3 Backlund变换
7 Hilbert定理
7.1 负曲率曲面上的渐近线网
7.2 常负曲率完备曲面上的整体渐近线网
7.3 定理的证明
8 Hartman—Nirenberg定理
8.1 预备引理
8.2 定理的证明
9 极小曲面的Bernstein定理..
9.1 共变微分和Laplacian
9.2 关于Gauss曲率的计算
9.3 极小图的Gauss曲率计算
9.4 Bernstein定理的证明
10 常平均曲率曲面
10.1 面积的变分
10.2 保体积的变分
10.3 Hopf定理
第四章 曲面的内蕴几何学
1 曲面上的向量场
1.1 曲面上的向量场
1.2 曲面上向量场的平行移动
1.3 向量场的奇点
1.4 抽象曲面上的向量场
2 测地线与完备曲面
2.1 测地线
2.2 指数映射exp
2.3 测地线的最短性
2.4 完备性
3 弧长的第一变分
3.1 曲线的变分
3.2 第一变分公式
3.3 第一变分公式的应用
4 弧长的第二变分及Jacobi场
4.1 弧长的第二变分公式
4.2 Jacobi场
4.3 共轭点
5 曲率与拓扑
5.1 曲率与Jacobi场
5.2 Gauss曲率非正的曲面
6 闭测地线与基本群
6.1 闭测地线与基本群
6.2 覆盖空间与闭测地线
6.3 紧致闭曲面上的闭测地线
第五章 高维欧氏空间的超曲面
1 基本公式
1.1 超曲面的结构方程和曲率张量
1.2 主曲率与平均曲率
2 积分公式
2.1 Minkowski积分公式
2.2 紧致凸超曲面
3 球面的刚性定理
3.1 非负Ricci曲率的紧致超曲面
3.2 常数数量曲率的紧致超曲面
4 极小超曲面的Bernstein型定理
4.1 关于第二基本形式的一个估计
4.2 稳定性不等式
4.3 Bernstein定理的推广
4.4 定理4.4的另一证明
5 常平均曲率的完备超曲面
5.1 常平均曲率图
5.2 常平均曲率超曲面的曲率估计
5.3 具有有限全曲率的常平均曲率超曲面
6 平均曲率流
6.1 平均曲率流方程
6.2 解的短时间存在性
6.3 度量和曲率的发展
6.4 紧致凸超曲面的收缩
附录A 欧氏空间点集拓扑概要
附录B 曲面的拓扑分类
参考文献...
扩展阅读:
图书 http://vipbooks.ninghaisen.com/book/B0011B8IRE.html
标签:
杂谈 |
戴季陶,(1891-1949)国民党。从最初宣传马克思主义,筹建中国共产党,到最后坚决反共。一路走来,十分之艰辛。国民党中唯一能够与中共思想抗衡的杰出理论家,在这过程中自杀两次,一次是1921年中共正式成立,国民党戴季陶不能左,后经商惨败跳江未遂;一次是1949年,解放军占领南京,戴季陶随国民政府败退广州后,服药自尽。
国民党多出几个戴季陶,想必就不是现在的结果了。只觉得他一生的才华太孤单,孤军奋战共产党,没有人配合。想当初,与陈独秀等人,朝夕相处,大谈马克思主义,互相交流思想,到后来筹建中国共产党,我想那一定是他最愉快的时光,尽管后来这(中国共产党)成为他最大的劲敌。
戴季陶指责共产党“只借中国国民党的躯壳,发展自己组织”“只单纯的利用国民党政治的保护力和经济的维持力,扩张自己的生命”。从整个历史来看,的确如此。觉得国民党失败的可惜。
一个人的信仰真的可以左右他的一生,而我们呢,信什么呢?
国民党多出几个戴季陶,想必就不是现在的结果了。只觉得他一生的才华太孤单,孤军奋战共产党,没有人配合。想当初,与陈独秀等人,朝夕相处,大谈马克思主义,互相交流思想,到后来筹建中国共产党,我想那一定是他最愉快的时光,尽管后来这(中国共产党)成为他最大的劲敌。
戴季陶指责共产党“只借中国国民党的躯壳,发展自己组织”“只单纯的利用国民党政治的保护力和经济的维持力,扩张自己的生命”。从整个历史来看,的确如此。觉得国民党失败的可惜。
一个人的信仰真的可以左右他的一生,而我们呢,信什么呢?
标签:
转载 |
本产品可用于儿童教育金规划、个人养老金规划、资产传承规划、合理避税规划、资产风险规避规划等。
投保示例 王先生,公司职员,为自己刚出生满30天的儿子王小天投保20份“鸿鑫人生两全保险(分红型)”和20份“附加鸿鑫人生加倍关爱重大疾病保险”,主附险基本保额都是2万元,年交保费12520元,10年交清,红利累积生息。

投保示例 王先生,公司职员,为自己刚出生满30天的儿子王小天投保20份“鸿鑫人生两全保险(分红型)”和20份“附加鸿鑫人生加倍关爱重大疾病保险”,主附险基本保额都是2万元,年交保费12520元,10年交清,红利累积生息。

保障利益王小天的保障利益如下:
1、祝福金:自合同生效日起,小天每年可领取1800元,直至终身。王先生指定领取日为小天的生日,将祝福金作为小天的生日礼物和成长纪念。
2、祝寿金:小天70周岁时可以领取一笔金额相当于已支付的主险保险费总额的祝寿金117200元。
3、上述祝福金和祝寿金若留存于公司,还可累积生息,持续增值。按照3%的年累积利率预测,生存给付累积账户金额到60周岁时可达302301元,到80周岁时可达753314元。
4、重大疾病关爱金及重大疾病保险费豁免:若小天被确诊初次发生附加险合同约定的重大疾病,将于重大疾病确诊后每年获得1800元重大疾病关爱金,直至身故,重大疾病关爱金如不领取,还可留存于公司累积生息;同时公司将豁免以后各期的主附险合同的保险费,被豁免的保险费视为已支付。
附加险合同生效或最后一次复效(以较迟者为准)之日起180天内,若小天因意外伤害以外的原因被确诊初次发生附加险合同约定的重大疾病,退还已支付的附加险保险费,附加险合同终止。
5、身故保障:若70周岁合同生效日对应日前身故,按身故时已支付的主险保险费总额与身故时主险保险单的现金价值两项中较大者以及身故时已支付的附加险保险费总额与身故时附加险保险单的现金价值两项中较大者之和给付身故保险金,主险合同及附加险合同终止;70周岁合同生效日对应日后身故,按主险基本保险金额2万元与身故时主险保险单的现金价值两项中较大者以及附加险已支付的保险费总额与身故时附加险保险单的现金价值两项中较大者之和给付身故保险金,主险合同及附加险合同终止。
6、红利分配:保单有效期内,可参与公司红利分配。
1、祝福金:自合同生效日起,小天每年可领取1800元,直至终身。王先生指定领取日为小天的生日,将祝福金作为小天的生日礼物和成长纪念。
2、祝寿金:小天70周岁时可以领取一笔金额相当于已支付的主险保险费总额的祝寿金117200元。
3、上述祝福金和祝寿金若留存于公司,还可累积生息,持续增值。按照3%的年累积利率预测,生存给付累积账户金额到60周岁时可达302301元,到80周岁时可达753314元。
4、重大疾病关爱金及重大疾病保险费豁免:若小天被确诊初次发生附加险合同约定的重大疾病,将于重大疾病确诊后每年获得1800元重大疾病关爱金,直至身故,重大疾病关爱金如不领取,还可留存于公司累积生息;同时公司将豁免以后各期的主附险合同的保险费,被豁免的保险费视为已支付。
附加险合同生效或最后一次复效(以较迟者为准)之日起180天内,若小天因意外伤害以外的原因被确诊初次发生附加险合同约定的重大疾病,退还已支付的附加险保险费,附加险合同终止。
5、身故保障:若70周岁合同生效日对应日前身故,按身故时已支付的主险保险费总额与身故时主险保险单的现金价值两项中较大者以及身故时已支付的附加险保险费总额与身故时附加险保险单的现金价值两项中较大者之和给付身故保险金,主险合同及附加险合同终止;70周岁合同生效日对应日后身故,按主险基本保险金额2万元与身故时主险保险单的现金价值两项中较大者以及附加险已支付的保险费总额与身故时附加险保险单的现金价值两项中较大者之和给付身故保险金,主险合同及附加险合同终止。
6、红利分配:保单有效期内,可参与公司红利分配。
产品特色
1、巧理财终生年年祝福金
自主险合同生效日起,每年都可领到相当于主险基本保险金额9%的祝福金,首期祝福金于合同生效日即可领取,无需长期等待。收益返还频率高、速度快,年年享有一笔稳定的现金流,轻松满足长期财务规划的需要。
2、巧保值 七十还本祝寿金
除每年可领取祝福金之外,在70周岁时,还可领取到一笔相当于已交主险保费总额的祝寿金,既保证了资金安全,又可用于养老生活支出,提高晚年生活的品质。
3、巧增值 复利累积红利金
本公司每年根据分红保险的业务经营状况,确定红利分配方案,您可以每年分享到公司经营的成果。祝福金、祝寿金和红利均可留存在本公司账户,以复利累积生息,收益升值空间可靠稳定,助您抵御通货膨胀。
4、巧防范抵御风险保障金
一旦投保,将拥有终身身价保障。在保障资金收益安全之外,还可防范身故风险。
5、巧关怀 加倍体贴关爱金
可附加鸿鑫人生重疾保险,组成更为全面的保障计划。若患约定的重大疾病且符合理赔条件,将每年获得一笔金额等同于祝福金的特设重大疾病关爱金,增强生活保障,加倍体贴呵护人生长路。重大疾病关爱金如不领取,还可留存于公司累积生息。
6、巧呵护 人性彰显豁免金
可附加鸿鑫人生重疾保险,若患约定的重大疾病且符合理赔条件,除可获得重大疾病关爱金之外,对分期支付保费的,本公司将逐期豁免主险和附加鸿鑫人生加倍关爱重疾险的剩余保费,为您减轻经济负担,而且还继续享有理财计划的各项权益,彰显人性关怀。
7、巧心思指定日期送礼金
可自由设置祝福金和祝寿金在每年及70 周岁时的领取日期,如生日、结婚纪念日、开学日等,使受益人在特定的日期收到一份特殊的礼物,赋予您的爱更深刻的含义。
自主险合同生效日起,每年都可领到相当于主险基本保险金额9%的祝福金,首期祝福金于合同生效日即可领取,无需长期等待。收益返还频率高、速度快,年年享有一笔稳定的现金流,轻松满足长期财务规划的需要。
2、巧保值 七十还本祝寿金
除每年可领取祝福金之外,在70周岁时,还可领取到一笔相当于已交主险保费总额的祝寿金,既保证了资金安全,又可用于养老生活支出,提高晚年生活的品质。
3、巧增值 复利累积红利金
本公司每年根据分红保险的业务经营状况,确定红利分配方案,您可以每年分享到公司经营的成果。祝福金、祝寿金和红利均可留存在本公司账户,以复利累积生息,收益升值空间可靠稳定,助您抵御通货膨胀。
4、巧防范抵御风险保障金
一旦投保,将拥有终身身价保障。在保障资金收益安全之外,还可防范身故风险。
5、巧关怀 加倍体贴关爱金
可附加鸿鑫人生重疾保险,组成更为全面的保障计划。若患约定的重大疾病且符合理赔条件,将每年获得一笔金额等同于祝福金的特设重大疾病关爱金,增强生活保障,加倍体贴呵护人生长路。重大疾病关爱金如不领取,还可留存于公司累积生息。
6、巧呵护 人性彰显豁免金
可附加鸿鑫人生重疾保险,若患约定的重大疾病且符合理赔条件,除可获得重大疾病关爱金之外,对分期支付保费的,本公司将逐期豁免主险和附加鸿鑫人生加倍关爱重疾险的剩余保费,为您减轻经济负担,而且还继续享有理财计划的各项权益,彰显人性关怀。
7、巧心思指定日期送礼金
可自由设置祝福金和祝寿金在每年及70 周岁时的领取日期,如生日、结婚纪念日、开学日等,使受益人在特定的日期收到一份特殊的礼物,赋予您的爱更深刻的含义。
购买提示:
1、投保范围:投保年龄:出生满30天至60周岁。
2、交费方式:保险费采用趸交、3年限交、5年限交、10年限交或20年限交的方式。
3、保险期间:保险期间为合同生效之日起,直至被保险人终身。
温馨提示2、交费方式:保险费采用趸交、3年限交、5年限交、10年限交或20年限交的方式。
3、保险期间:保险期间为合同生效之日起,直至被保险人终身。
(1)如需咨询或购买,欢迎随时联系;
(2)联系方式:博客评论、留言,QQ 1966951883(注明咨询理财),或者发邮件到aisinuo@sina.cn。
(3)本文仅供参考,所演示的红利是不确定的,详细产品内容以条款为准。
(2)联系方式:博客评论、留言,QQ 1966951883(注明咨询理财),或者发邮件到aisinuo@sina.cn。
(3)本文仅供参考,所演示的红利是不确定的,详细产品内容以条款为准。
标签:
转载 |

如想购买本期ILOOK,请到http://ilookmagazine.taobao.com/
希望的核爆炸
九十年代初,我认识一个官员,他在一个中央研究机构工作,他的研究项目是中国的改革,他穿得破破烂烂的,皮鞋总是张着嘴,拎着一个旧得不能再旧的公文包,全国到处乱跑。我问他到底在研究啥,他总是笑着说:“我什么都不研究,我是销售员,我在全国推销希望。”
二十年来,我一直记得这句话,现在这个希望推销员已经是一个副部级的干部了。三十多年来,希望正是改革开放的真正动力。
写这篇文章的时候,正是日本地震后的一周,国内有人在抢盐,大家都怕日本会发生核爆炸。我突然觉得希望就是日本福岛的核电站。曾经一度,点亮了无数人的生活,希望是一种最原始的动力,能够使很多人跟通了电一样拼命地干活。我自己也不例外,CIMG刚成立的时候,我曾经希望挣很多钱,希望公司上市,希望去纽约证交所敲钟(和我的朋友们一样)。第一次结婚希望白头到老,第二次希望并肩奋斗,第三次希望写本中国人的《永远的普罗旺斯》。
希望的破灭就是核爆炸,其结果是向社会散发出无数浮云辐射后,大多数人会产生不可抗拒的挫折感,对生活毫无追求,不是绝望也是好死不如赖活着。
我们的社会似乎已经经历了无数次这种核爆炸,以至于“神马都是浮云”成为了流行语。这种失落,对于我们的社会还是一件新鲜事物,而在西方,浮云已经飘了N 多年了。
这就终于扯到我们这期的主题:浮云。德国的马克思主义哲学家Ernst Bloch 在他的《希望的准则》一书中写道:
“不能从根本上改变我们的看法就不可能达到社会主义。有些东西从一个理性的技术社会去看似乎只是‘白日梦’或‘逃避’。而实际上,从一个新的角度去分析,这些都是对一个新的、更加人性的社会制度的期望,这种表现虽然幼稚,但却是真实的改革的替身。”
我的理解是浮云并非完全消极,这种态度迫使人们去追求一种新的社会变革,一个更加人性、更加公正的和谐社会。
正如 Bloch 所说,我们要用不同角度去诠释“浮云”,而我们当然是用时尚的角度去看浮云这件事情,时尚本身就是浮云,而从这个云堆里面看社会,看到失望、甚至专制都有一套自己的审美。特此我们想让大家关注两部作品:
一是上海摄影艺术家马良的作品,早在几年前,他就已经把“浮云”纳入了他的创作主题。二是小说《华氏451度》。网上有卖的,是一本背景为美国的科幻小说。
刊物是我们很认真做的,这篇导语也是我做了功课后写的,但是劝大家还是不要想太多,毕竟浮云里面仍然有希望。
标签:
转载 |
赢在长庆
长庆石油报记者 王静
2009年对于长庆来说,注定不寻常。
一方面,世界经济持续低迷,国内石油石化行业纷纷限产关井,整个中国石油原油生产调减700万吨,调减产能建设400万吨,上万口油井被迫关闭,上百部钻机停钻,勘探和炼化版块投资锐减,炼厂负荷降低,油气销售不畅,库存上升,经济形势异常严峻;另一方面,却是中石油做出的“保大庆稳产、促长庆上产”的战略决策,“投资不减、产量不减”的“双不减”政策,让金融危机背景下的长庆油田优势勃发,马达加速,依然保持了昂扬向上的发展势头。
首季开门红让处在经济“严冬”中的每一个长庆人感受到了春天般的温暖,而3000万和5000万的高远目标更让长庆人感到了肩上沉甸甸的责任。正处在发展快车道上的长庆油田,在全球经济萎缩的形势下之所以要继续加大规模上产,加速发展,是国家石油战略安全的需要,更是长庆作为中国石油战略接替区和中国陆上天然气枢纽的重要地位所决定,为国分忧是此时长庆必然要担当的神圣使命。
到2015年,当长庆顺利实现5000万吨油气当量规划目标,谁将是最大的受益者?每个人的答案都会不尽相同。但从长庆这几年大发展带来的变化中我们不难看到,发展是解决一切问题的关键,大发展给员工带来的将是可持续的永久的回报,数万员工既是5000万吨的创造者,也始终是5000万吨最大的受益者。
岁月有多长,创业的路就有多长
从某种意义上讲,精神文化就是生产力,是企业跨越式发展的内在动力。
在38年的岁月长河中,几代长庆人殚精竭虑,以“我为祖国献石油”的豪迈情怀奉献能源,使长庆从一个不为人知的油田,成长为中石油第二大油田,在创造物质财富的同时,也给我们留下了宝贵的精神财富。
长庆油田沉积了丰厚的企业文化底蕴。“自力更生、艰苦奋斗”的延安老区精神,在油气田的每一寸热土闪烁光芒;“三老四严、四个一样”的大庆精神和“宁肯少活二十年,拼命也要拿下大油田”的铁人精神,更是激励一代代石油人扎根陕甘宁,为“发展大油田,建设大气田”孜孜不断地追求进取。
如果说,老区精神、铁人精神是推动油田发展的精神源泉的话,那么,具有鲜明个性特色的“攻坚啃硬,拼搏进取”的精神理念,无疑是长庆油田由小到大,油丰气盛的精神支柱。就是在这种精神的支撑下,使长庆油田在“三个石头支口锅,三顶帐篷搭个窝”的艰苦条件下,创造了从陕西咸阳“人拉肩扛跑步数百公里上陇东”参加油田会战及“磨刀石上闹革命”开发低渗透油田的奇迹。
在38年的发展中,长庆人在发展中继承,在实践中创新,确立了自己的信仰追求,将自已的前途、企业的命运与国家发展联系起来,树立为祖国献石油的神圣使命和崇高责任。多年来,长庆人义不容辞地承担确保国家能源安全的职责,把忠诚于石油事业的选择,做为实现自已终身奋斗的目标,献了青春献终身,献了终身献子孙,代代薪火相传,骨子里已镌刻下了忠诚于祖国的烙印。国家的需要就是长庆石油人的需要,神圣使命滋生出他们为国家寻找大油田、大气田,为国家多生产石油、天然气的不竭动力。
长庆人用自已的行动诠释了神圣使命的含义。上个世纪70年代,长庆还是一个无人知晓的油田;80年代,原油产量上到百万吨;90年代,原油产量达到500万吨以上;进入新世纪,原油产量突破1000万吨,发现了7个大气田,天然气产量上百亿立方米,2007年油气当量跨超2000万吨,成为中国石油发展最快的油田。
从1997年开始,天然气进入西安、北京。如今,长庆天然气北上呼和浩特,西输银川,东进石家庄、北京、天津,南下郑州、上海,已实现给18个大中城市供气,四通八达的外输管线区域,已形成了一大批天然气发电、化工产业。塞外荒漠的石油人和周边城市千家万户居民的日常生活紧紧联系在一起。长庆人用无私的创造,温暖了祖国的大江南北。
2003年,西部大开发标志性工程西气东输管道全线贯通,长庆天然气要作为“先锋气”奔向大上海。当年必须增加27亿立方米的产气能力,相当于一年内要完成前五年的工作量,当时正值“非典”全国处于高度戒备,产能建设却如火如荼的展开。在大气田火热的生产现场,员工长期不能回家,许多家人带着孩子,赶往气田“探亲”。10月6日,当长庆天然气胜利到达上海的那一天,许多长庆人留下了热泪。在西气东输表彰大会上荣立一等功的采气一厂员工说,人一辈子能遇到几件全国关注的大事情,能作为给北京、给上海生产天然气的一名工人,这样的经历值得一生骄傲和自豪。2004年冬季,由于北京、西安地区天然气用户快速增长,用气量急剧上升,长庆宁肯减少油田自用气,也要确保向北京、西安安全足量供气,受到社会各界的称赞。
正是有了强烈的责任感和使命感,才有了这样的价值选择。长庆企业文化,正是从地域文化中捡石,在军队文化中淬火,于石油文化中炼金,在大项目大发展中亮剑,推动着长庆油田跃上发展新高点。这种融入了使命与责任的长庆文化,决定了长庆人必然选择奉献和勇气,来忠诚使命和践行责任。
这些文化基因,都有着相同的优秀特质,即强大的执行力,勇于奉献的精神,甘守寂寞的情怀和不轻言弃的坚韧,锻造出长庆这支“特别能吃苦、特别能奉献、特别能创造”的英雄队伍,展现了“高度的凝聚力、顽强的战斗力和坚定的执行力”,成为长庆发展的文化基础和队伍保障。
名扬油田内外的“好汉坡”,由于坡陡涧深,当地人叫它“阎王坡”。近20年来,王三计量站的员工为了巡护山顶上的11口油井,每日徒步攀爬海拔1300米、坡度70度的陡坡,硬是靠信念踩出了一条创业之路,成为长庆人不畏艰难,矢志奉献精神的一个缩影。2008年7月,中国石油天然气集团公司总经理、党组书记蒋洁敏和参加中国石油延安干部会议的代表一起攀上“好汉坡”后,被长庆人历经磨难、无畏艰难、勇攀高峰的新时期创业精神和热爱石油、无私奉献的敬业情怀所感动,欣然题写下了“好汉坡、石油河、英雄人”9个刚劲有力的大字。如今,“好汉坡”精神在“发展大油田,建设大气田”的伟大实践中,如一颗夺目的宝石,正在绽放出绚丽的异彩。
曾经是好汉坡第一任站长的梁冬介绍:我们的工作性质要求每天必须对油井两次的巡护。遇到下雨天我们就是拿着铁锨拄着,相互搀扶着慢慢地去攀爬。遇到下雪天,就是用铁锨、用扫帚把雪扫干净,然后在保证安全的前提下,再上去巡护。我们做到了365天风雨无阻。
这就是长庆人的勇气。勇者无畏勇者强,因为这是为祖国而勇,长庆人义无反顾。
在安塞县贺家沟海拔1600多米的高山上,驻扎一个计量接转小站,它就是安塞油田的第一个女子站——郭秀玲站。郭秀玲站是安塞油田的咽喉站,安塞油田每天生产的上千吨原油,就是从这里转输出去的。这里春秋两季经常狂风肆虐,冬夏时节寒暑难当。可就是在这种艰苦的条件下,这个由17名平均年龄只有25岁的女工组成的集体,却在大山里默默地坚守了1800多个日日夜夜,确保了油田“大动脉”的畅通。
郭秀玲说:老一辈石油人留下的精神财富,就是要在我们这一代人身上得到传承,长庆,是我们的长庆,我们有责任靠勤劳的双手去创造长庆美好的明天。也许,这就是郭秀玲当初放弃医生这个理想职业,跑到大山深处来当一名普通石油人的初衷。
这就是长庆人的胸怀。胸中有爱,这是大爱,爱事业,爱祖国,总是无怨无悔。
长庆石油人的美好年华属于高原大漠,员工们以质朴和爱心感动着厚重的大山。南一增压站座落在陕西靖边县一个山沟里,站上有6名采油女工,站外不足百米的地方有一所小学。2003年9月,一次偶然机会,女工们发现这个学校只有一名老师,4个年级23名学生混用一间夏不遮雨、冬不挡寒的教室。她们与村干部联系,利用休息时间义务给山村小学生上课,为从来没唱过歌、跳过舞的孩子们增加了音乐、舞蹈、美术等课目。5年来,南一增女工累计给这些山村小学生教课1600多次。使这原来在学区统考一直倒数第一的学校,2005年以来已经连续两年夺冠。中央电视台《当代工人》栏目曾现场录制了反映这个站采油女工爱心助学的节目。
这就是长庆人的风采,他们有无比坚强的意志,也有一颗柔软的心。点点滴滴,春风化雨,洒向人间。
好汉坡、郭秀玲站,是长庆油田艰苦创业的缩影。在沟壑纵横或者黄沙漫天的环境中建成可望接替大庆的油气田,其实已经成为一种内涵丰富的国企文化现象。而统领这种文化的核心精神,则是一般企业难以企及的。
一批批能够体现和反映长庆油田个性特点的精神成果层出不穷。安塞油田的“好汉坡”、陇东油田的“流芳亭”、靖边气田的“陕参1井”等,不但成为对员工进行思想教育的主阵地、活教材,而且成为外界了解长庆的文化窗口。这些代表着长庆人“爱国、创业、求实、奉献”精神的闪光亮点,昭示着一批又一批的长庆员工,积极投身“发展大油田,建设大气田”的火热一线。
作为5000万吨的创造者和见证者,每一位长庆员工都是大写的人。我们的身上,流淌着先辈的血液,我们的脑海里,刻印着先辈的精神。解放军文化、石油文化和老区文化,融进第一代长庆人的血液里,推动了长庆的大发展,也必将成为今天长庆员工的信仰与追求,为5000万吨目标的实现,振奋精神,脚踏实地,进行前所未有的卓绝的创造。
心有多大,舞台就有多大
人生能有几回搏,大海召唤弄潮儿。
长庆5000万吨的高远目标,是一个载入史册的重大事件和伟大创造,作为发展长庆、奉献长庆的亲历者、见证者、创造才和推动者,几代长庆人的夙愿集中到了我们这一代人身上,长庆人迎来了千载难逢的发展机遇。一场历史性的静悄悄的大会战,为新时期的长庆人搭建起了更加灿烂、更加诱人、更加广阔的人生舞台,为更多的员工在大发展的伟大实践中提供了展示才智、提升能力、锤炼成长、实现人生价值的机会。长庆人在创造丰厚的物质文明的同时,也在享受着崇高的精神的回报,长庆人为此自豪,为此骄傲。
近年来,油田公司为员工创造了良好的成长空间,搭建起了展示聪明才智的广阔舞台:长庆油田不仅要出油气,更要出人才、出精神,长庆的大发展需要一支一专多能的高素质人才队伍。
油田公司为员工成长、成才开辟了多种渠道,搭建宽广平台,不论是遍及油区的大培训、大练兵、大比武活动,还是积极承办或参与的甘肃省、陕西省、宁夏回族自治区及集团公司技能大赛;不论是丰富多彩的班站长培训、转岗培训、岗位适应性培训、企业文化、HSE管理等培训,还是广泛开展的技能鉴定、技术等级晋升和职业资格认证,都为员工发展成长畅通管道,提升了员工队伍整体素质,支撑了油田大发展。
多年来,长庆油田一直积极探索适应社会发展和企业实际的人才培养机制,探索新型人才培养方式,逐步完善了自主培养、合作培养、外来引进三者互补的人才培养模式。长庆油田目前已经建立起了经营管理人员能力建设培训、专业技术人员技术创新培训、操作技能人员技能提升培训以及在职人员学历提高培训为主要内容的,大规模、广覆盖、多层次、有重点的运行机制和培训工作格局。
为保证人才队伍建设扎实有效开展,长庆油田各单位结合本单位的实际和一线作业队伍生产施工特点,开展了灵活多样,切合生产作业实际的培训方式,培训工作在基层得到较好的落实。在培训时间上,坚持了“宜长则长,宜短则短”的原则,不搞一刀切,在培训形式上,采取了集中与分散相结合,请进来与送出去相结合、脱产与业余相结合,内培与外培相结合,岗位练兵与专题训练相结合等多种培训形式,使整体培训效果较往年有了明显的提高。
从基层建设管理十法的总结应用到基层文化示范窗口的不断涌现,从标准化的广泛推行到数字化的建设,一批新时期的优秀员工脱颖而出,一大批员工正在完成由传统管理到现代管理角色的转换。仅2008年以来,就有2万余名员工参加了各种培训,5600余人参加了公司技能大赛,100余人参加了省级职业技能竞赛,6000余人进行了技术等级鉴定,80多人申报了省部级技术状元、技术能手称号,32人破格晋升为技师、高级技师。油田公司也先后荣获陕西省、甘肃省职业技能大赛团体金奖,并在集团公司技能竞赛中取得11枚奖牌。
长庆油田采取积极有效的激励措施激发人才的积极性,使人才发展与企业发展同频共振、同轨并进、同心相融。为了最大程度的发挥人才的作用,长庆油田倾尽全力营造氛围,制定激励机制,让人才的能量充分释放,为油田大发展贡献力量。每年提供专门的项目资金,用来支持和奖励员工为企业改革创新提供新思路、新方法、新科研。凡是有发明、创造、参加科技攻关、发表学术论文、获得国家专利的员工都可以从中得到资金奖励和职位晋升。在2008年,油田公司还选派127名劳动模范、优秀员工出外学习培训,安排810名优秀员工、技术骨干进京观看奥运会、残奥会,多管齐下的激励效应得到最大程度的放大。油田大发展的喜人形势、呈现出的健康发展氛围、珍惜人才的做法,无一不吸引着众人的关注,一批又一批的人才纷至沓来,2008年,就先后有千余名本科以上人才加入到长庆油田的员工队伍之中,投身鄂尔多斯盆地的开发建设。
长庆油田第一采油厂王十六转隆重举行“郭秀玲站”命名大会;采油二厂培训中心专职教师梁庆辉开发的“四化”培训法被命名为梁庆辉“四化”教学培训法,受到表彰奖励;2007年在采油四厂成立并揭牌“程少春工作室”,给予工人发明家程少春最大肯定的同时,也为创建“技能型、知识型、创新型”的员工队伍平台提供了一个平台。
现在,长庆油田已经建立健全了中长期激励机制,制定了多层次的员工培训体系,使优秀、骨干员工能够分享公司成长的成果。如今,这些优秀、骨干员工大多已经走上了管理、技术等重要岗位,成为长庆油田新生的中坚力量。
“全国知识型职工优秀个人”、采油二厂木二转站长马琴,将“爱心、诚心、用心、精心、恒心”应用到班站管理中,打造出了一支真情相连、主动工作、永不等待、坚强有力的自主管理团队,她的管理方法很快被油田公司命名为“马琴工作法”在全油田得以推广,成为班组管理的亮点。
在陕北吴起,一块交织着革命先烈红色印记与石油工人金色希望的热土上,采油三厂新寨作业区的经理谢银伍,从当初的一名普普通通的采油工一路走来,他将自己的知识、才华和理想,放置于油田大发展的舞台上尽情展示,放置于大山深处艰苦的环境中不断淬火、锤炼,逐步成长为一名采油队长、作业区经理。谢银伍干事爱动脑子,是个出了名的“智多星”。他倡导淡化领导,突出团队作用,坚持“心通行同合作双赢”的理念,运用“工作上分、思想上通、目标上和”的工作方法,实施“1+2”用工管理模式,为市场化用工探索出一条路径;培育“新天地”文化,铸就精神动力;探索出了“五自”管理法,为五型班组建设植入新思想。凭借一腔热情,挥洒创业激情,谢银伍的先进管理思路和实践在他倾心付出的土地上结出了硕果。队伍稳定、管理有序、高效运行、产量攀升……作业区各项工作呈现良性的运行态势,展示出“和谐发展、彰现人文”的景象。2007年1月,采油三厂产建主力区块由靖安油田转至吴起油田,谢银伍被委以重任,担任新成立的新寨作业区经理。他创新有效管理,提出“重点工作日常化、日常工作高效化”的思路,制定了《多元多级化程控管理办法》,实施“两超两全两化”组织和“一小两大”扁平化管理模式,促进基层管理水平提高。他管理的新寨作业区曾经创造出日产9换百字头,突破2000吨,成为国内特低渗透油田采油作业区原油日产水平最高纪录,2009年,谢银伍被树立为“中国石油榜样.好干部”典型。
采油七厂白豹作业区采油六井区党支部书记兼白四增压站站长周阿妮,工作5年来,不论是在操作岗位,还是在管理岗位,她都认真、主动对待每一项工作。用她自己的话说,只有把工作主动干好了,管理才有“号召力”,团队才能拧成一股绳,团队每个成员才能充分发挥智慧和力量。在周阿妮的感染和带领下,白四增压站先后获得油田公司“巾帼建功示范岗”、“青年文明号”、“基层建设示范点”等荣誉称号;“周阿妮亲情管理法”在2008年油田公司工作会议上,被作为典型示范在全公司进行推广。周阿妮也先后被评为油田公司2007年第四届“十大杰出青年”,采油七厂“首届十佳青年”等。
这些长庆人,和石油在一起,他们是大写的人,在各自平凡的工作中追求卓越、创造价值,他们是数万名为油奉献、为气拼搏的一线员工的杰出代表,他们的名字将永远镌刻在长庆油田的发展史上。随着长庆实现5000万吨的步伐加速,还会涌现出更多的郭秀玲、刘玲玲、谢银武,梁庆辉这样的优秀人才,在长庆的大舞台上尽情驰骋,越来越多的员工,将在长庆这片土地上找到属于自己的人生座标。
发展有多大,回报就有多大
发展长庆就是发展自己。实现5000万,是每一个长庆人最大的福祉。
从昔日的“三块石头架口锅,三个帐篷搭个窝”到今天风景如画、生活设施齐全的生活小区;从设施简陋、光秃秃的小小井站,到掩映在绿树丛中的“一线之家”,长庆的大发展,回馈给员工的是丰厚的物质回报。
冉新权总经理不止一次地强调:“长庆油田的快速发展要惠及员工、以人为本。主要体现在保证员工收入持续稳定增长、一线员工工作和生活条件不断改善、基本解决职工子女就业问题和大力解决职工住房问题等方面。要解决员工的后顾之忧,进一步增强队伍凝聚力。”
以人为本,将企业发展成果惠及广大员工群众,实现企业与员工利益的共同发展。这在长庆油田,不仅仅是一句承诺。
近几年来,长庆在在薪酬分配、福利待遇及社会保险,改善一线员工工作、生活条件,解决子女就业和帮扶困难群体,加强矿区建设、提高矿区服务质量等方面开展了大量细致而卓有成效的工作,使员工的生产生活条件得到了很大改善。
长庆油田点多、线长、面广,绝大部分井站和施工点分布在陕、甘、宁、内蒙古的偏僻山区,员工长年驻守井站,远离城市,对于精神文化生活有着强烈需求。近年来,改善一线员工的工作生活条件被提到了与油气发展同等重要的位置。油田公司心系一线员工道路安全,以“建养并重、保障生产”为原则,投资上亿元,重点对员工生活区、大站大库、油气产量高、井站数量多、车辆通行量大的油气区主干道进行升级改造,完善主干道路网络和道路安全防护设施,大大降低了安全风险。开展“送健身器材、送整体厨房、送文化活动”进井站活动,为一线井站配置图书报刊、健身器材和文体用品,营造良好的井站人文环境,加大温暖基金向基层文艺团体、基层文体协会的投入力度,鼓励员工参加文艺创作、出版个人作品、实现个人价值。坚持疗养疗休向一线员工、艰苦岗位、劳模先进“三个倾斜”,使广大员工特别是一线员工在繁忙的工作之余得到了身心的放松。
2008年,油田公司在改善一线员工生产生活条件方面更是下了大力气,做了大投入:投资3.08亿元建设和改造前线生产倒班点53个,解决油区单井看护点100多个,井场值班室246间,一线100个生产场所环保厕。投资2000万元安装净化水装置、修建水窖等,解决老油田一线员工生活饮水困难问题。同时下拨3000万元解决野外生产一线“员工之家”建设。
现在,无论在采油或采气一线,都能看到掩映在绿树红花丛中的井站。视频监控和采油数据自动采集技术,让采油工不用出门,坐在计算机前就能对井站的工况实时监控;工作环境不断改善,劳动强度大大降低。一线井站不但有阅览室、电视,有澡堂,而且有简易网吧和话吧,员工工作午餐免费供应,住宿全部实现了公寓化。井区和大站建立的图书室和阅览室,使员工一年四季都能看到不同内容的图书和杂志,员工们可以自我充电获取新知识;在井区建立就医点及邀请专家上门就诊,解决了一线员工的看病难题;新春季节,从身边的大棚里就能吃到比城市居民吃的还新鲜的各种蔬菜……
长庆油田在改善一线生产生活条件的同时,不断配套完善后勤基地。从“三块石头支口锅”、“一顶帐篷安个家”,到今天定居大中城市,长庆人用了30多年的时间。自1970年石油勘探会战至今,共形成了综合性基地和生活基地52个,主要分布在陕西、甘肃、宁夏等省区的26个市县。长庆油田本着以人为本、方便管理、改善生活的原则,优化生产生活布局,已经形成重点建设的西安和银川两个大的总部基地和生活基地,并在不断配套完善陇东、延安、靖边、定边、顺宁、榆林和乌审旗等七个生产基地。目前长庆油田生活小区占地总面积2800多公顷,已建职工住宅61010套,建筑面积541万平方米,驻矿居民达15万余人,基本适应了油田快速发展的需要。
位于西安市北郊西安经济开发区中心地段的兴隆园,集生产、科研、工贸、文教卫生、生活服务为一体,已成为设施配套齐全,院落整洁、环境优美、治安秩序良好的新型石油基地。在西安市泾河开发区,新建的长庆龙凤园小区和泾渭苑小区职工相继搬迁新居。从上世纪90年代末开始承建,到今天建成占地面积2040亩,建筑面积近110万平方米,住宅10252套,总投资15亿元,有3万多职工家属入住的银川燕鸽湖基地,长庆人只用了不到十年的时间。目前,这座聚集了宁夏片区长庆石油人的现代化生活社区,拥有优美的中学、小学校园,设施健全活动中心和人工景观湖,成为长庆职工家属安居之地。除了西安、银川两大重点建设总部基地和生活基地之外,长庆油田在陇东、延安、靖边等城市的生活小区也在蓬勃发展,长庆石油人落户大中城市的梦想已经成为现实。
随着公司的大发展,长庆油田还不断提高员工的生活保障水平。2001年开始先后设立了公司“温暖基金”、机关干部助学基金及员工大病互助基金,对困难或因特殊情况致贫的员工实施生活救助、医疗救助和子女入学的一体化帮扶救助。建立了团体综合福利保障,实施一线员工免费就餐,设立了员工就医绿色通道,全方位解决了员工的后顾之忧。
员工子女就业问题一直牵动着长庆油田领导的心。2008年,公司接收高校毕业生,在专业对口、择优录用的前提下,优先考虑油田子女。在该年录用的非主体专业高校毕业生中,油田子女占到了非主体专业高校毕业生接收总数的87.5%。不仅如此,公司为了大发展储备人力资源和解决油田子女就业,长庆石油学校招生全部改为录用油田子女。去年,长庆油田解决油田职工子女就业1463人,是长庆油田历史上解决最多的一年。
为了提高有偿解除劳动关系人员在基地服务类岗位再就业劳务报酬、再就业困难补助、劳动家属生活补贴标准,2008年,安置再就业人员3007人,领取再就业困难补助2013人。再就业人员劳务报酬由原标准每人每月638.5元调整为746元;再就业困难补助由原标准每人每月362.2元调整为436元;劳动家属生活补贴由原标准每人每月160、180元分别调整为210、230元;修订完善了《长庆油田分公司困难职工帮扶管理办法》,理顺整合了公司困难员工生活帮扶、医疗帮扶、助学帮扶、就业帮扶及工作机制。2008年下拨帮扶资金2400万元,共计慰问各类困难员工5138户次。
与此同时,长庆油田在提高一线员工免费就餐标准、薪酬分配、福利待遇及社会保险方面也做了大量卓有成效的工作。从2008年7月1日起工作单位不在油田生活基地的误餐补助标准,误餐补助由13元和10元统一提高为18元。为14724
名合同化员工、合同制员工岗位(技)工资晋档,年增资530万元。在集团(股份)公司建立统一的企业年金制度的基础上,为保证已退休人员享受的补充养老保险人均267元不受影响和即将退休人员待遇不降低,将逐年筹资近3亿元实施油田公司企业年金过渡办法。为18199名员工投保团体保险,并提高了基本医疗最高支付限额。从2008年1月1日起,基本医疗最高支付限额由56700元提高到66260元,增加9560元。调整员工和退休人员因病、非因工死亡供养直系亲属生活困难补助费标准,人均月增加90元。修订完善了《长庆油田公司关于组织好员工疗休养工作落实带薪休假制度工作的意见》,组织劳模先进疗休养279人,员工疗休养2000人。将员工疗休养和落实带薪年休假制度工作结合起来,在保证生产建设工作正常进行的同时,最大限度地组织员工休假、休养,积极推进整合后员工疗休养工作的顺利开展,将企业发展成果惠及全体员工。
对员工的关爱在继续,在深化,一项项惠民政策,像一场场如酥春雨,滋润了广大员工的心田,更激发了每一个长庆人发奋创造的激情和活力。
沧海横流,方显英雄本色。
从当年数万人“人拉肩扛跑步上陇东”、挺进年产量百万吨的人海会战,到如今数万人按照“大油田管理、大规模建设”发展思路、年产挺进3000万吨的静悄悄的科技大会战;
从历经十年发展的痛苦徘徊,人才“孔雀东南飞”,到如今日新月异的大发展,成为中国石油增储上产的领跑者,吸引大量研究生、博士生落户到这片创业热土;
从当年“三个石头支口锅,三顶帐篷搭个窝”的艰苦生活,到如今在大中城市安家落户,拥有花园般美丽的家园和一流的社区服务;
从当年外界陌生和茫然的眼神,到如今知名度和美誉度大幅提升,像当年的大庆一样备受世界瞩目……
长庆的大发展,回馈给员工的是丰厚的物质回报。
面对来之不易的大发展局面,身处和谐奋进的良好氛围,吹响5000万吨的强劲号角,每一位长庆人都已做好了准备,为长庆的大发展尽心竭力。这样,当我们回首往事,不会因碌碌无为而懊悔,更不会因错失良机而遗憾。当我们看到欣欣向荣的发展景象,看到幸福指数不断提升的子孙后代,我们一定会倍感骄傲和自豪,因为,这一段辉煌的发展史,这一个充满希望的长庆,这样一个美好的未来,我们亲历,我们见证,更由我们创造!
长庆,这个正在西部扬帆起航的巨轮,正以它磅礴的气势,百折不挠的勇气、一往无前的信念,让世人看到了中国石油工业的新希望。
长庆,是我们的长庆,是我们的家园。铸就5000万吨丰碑,长庆奉献给中国和世界的,是一个奇迹。这个奇迹,将从这一代长庆人手中诞生!

 加载中…
加载中…

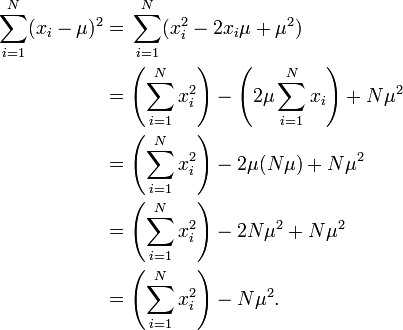
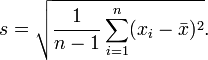



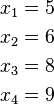
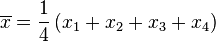


![\sigma = \sqrt{\frac{1}{4} \left [ (x_1 - 7)^2 + (x_2 - 7)^2 + (x_3 - 7)^2 + (x_4 - 7)^2 \right ] }](http://upload.wikimedia.org/wikipedia/zh/math/1/f/7/1f7d72737d4cdd6dd0332b4dfc606a50.png)
![\sigma = \sqrt{\frac{1}{4} \left [ (5 - 7)^2 + (6 - 7)^2 + (8 - 7)^2 + (9 - 7)^2 \right ] }](http://upload.wikimedia.org/wikipedia/zh/math/6/5/6/6560ac4b798b90789db7a4248692077e.png)


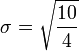





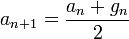



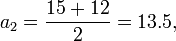



![G = \sqrt[n]{\prod_{i=1}^n x_i} = \sqrt[n]{x_1 \cdot x_2 \cdots x_n}](http://upload.wikimedia.org/wikipedia/zh/math/4/3/c/43cea9aee871f9ad5ec664fcf4f9e2e3.png)




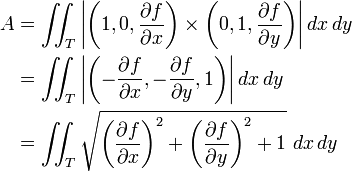

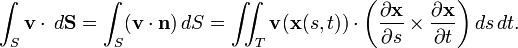

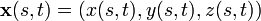
![场论/曲面的积分(高斯公式、格林公式、斯托克斯公式) \iint_D \left[ f_{1} ( \mathbf{x} (s,t)) \frac{\partial(x,y)}{\partial(s,t)} + f_{2} ( \mathbf{x} (s,t))\frac{\partial(y,z)}{\partial(s,t)} + f_{3} ( \mathbf{x} (s,t))\frac{\partial(z,x)}{\partial(s,t)} \right]\, ds dt](http://upload.wikimedia.org/wikipedia/zh/math/0/9/d/09d4c43acaf269e54f65ffef9174d54f.png)














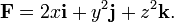










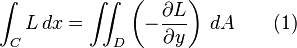



![场论/曲面的积分(高斯公式、格林公式、斯托克斯公式) =\int_a^b\!\!\int_{g_1(x)}^{g_2(x)} \left[\frac{\partial L (x,y)}{\partial y}\, dy\, dx \right]](http://upload.wikimedia.org/wikipedia/zh/math/3/3/d/33d654ab5d0c1af5db56b9741638d931.png)

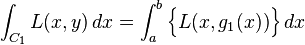
![场论/曲面的积分(高斯公式、格林公式、斯托克斯公式) \int_{C_3} L(x,y)\, dx = -\int_{-C_3} L(x,y)\, dx = - \int_a^b [L(x,g_2(x))]\, dx](http://upload.wikimedia.org/wikipedia/zh/math/c/4/1/c414fd50f39dccb536e87c0519f773b6.png)


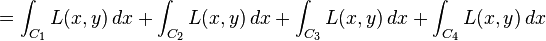
![场论/曲面的积分(高斯公式、格林公式、斯托克斯公式) = -\int_a^b [L(x,g_2(x))]\, dx + \int_a^b [L(x,g_1(x))]\, dx\qquad\mathrm{(4)}](http://upload.wikimedia.org/wikipedia/zh/math/4/a/8/4a8ea1e07dac7011641487530c9167ee.png)




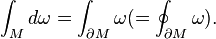

No comments:
Post a Comment