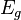 )。
)。能带结构可以解释固体中导体、半导体、绝缘体三大类区别的由来。材料的导电性是由“传导带”中含有的电子数量决定。当电子从“价带”获得能量而跳跃至“传导带”时,电子就可以在带间任意移动而导电。
一般常见的金属材料,因为其传导带与价带之间的“能隙”非常小,在室温下电子很容易获得能量而跳跃至传导带而导电,而绝缘材料则因为能隙很大(通常大于9电子伏特),电子很难跳跃至传导带,所以无法导电。一般半导体材料的能隙约为1至3电子伏特,介于导体和绝缘体之间。因此只要给予适当条件的能量激发,或是改变其能隙之间距,此材料就能导电。
能带理论
维基百科,自由的百科全书
| 建議将能带结构併入本條目或章節。(討論) |

晶体硅的能带结构示意图
自20世纪六十年代,电子计算机得到广泛应用以后,使用电子计算机依据第一性原理做复杂能带结构计算成为可能(不过仍然非常耗时,一次典型的能带结构自洽计算在普通工作站上往往需要花几个小时甚至一周多的时间才能完成)。能带理论由定性发展为一门定量的精确科学。
目录[隐藏] |
[编辑] 能带结构简介
固体材料的能带结构由多条能带组成,能带分为传导带(简称导带)、价电带(简称价带)和禁带等,导带和价带间的空隙称为能隙(即右边第二副图中所示的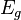 )。
)。能带结构可以解释固体中导体、半导体、绝缘体三大类区别的由来。材料的导电性是由“传导带”中含有的电子数量决定。当电子从“价带”获得能量而跳跃至“传导带”时,电子就可以在带间任意移动而导电。
一般常见的金属材料,因为其传导带与价带之间的“能隙”非常小,在室温下电子很容易获得能量而跳跃至传导带而导电,而绝缘材料则因为能隙很大(通常大于9电子伏特),电子很难跳跃至传导带,所以无法导电。一般半导体材料的能隙约为1至3电子伏特,介于导体和绝缘体之间。因此只要给予适当条件的能量激发,或是改变其能隙之间距,此材料就能导电。
[编辑] 理论基础
对于理想晶体,其原子服从晶格排列,具有周期性,因而可以认为离子实的势场也具有周期性。晶体中的电子在一个周期性等效势场中运动,其波动方程为: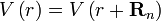 为周期性等效势场,
为周期性等效势场, 为波函数,
为波函数, 为普朗克常数,
为普朗克常数, 为质量,
为质量, 为微分算符,
为微分算符,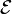 为能量
为能量[编辑] 近自由电子模型
能带理论认为,固体内部的电子,不是被束缚在单个原子周围,而是在整个固体内部运动,仅仅受到离子实势场的微扰。本征波函数的主部是动量的本征态,散射只给出一阶修正。这个模型只对少数晶体(如碱金属)适用。[编辑] 布洛赫波函数
布洛赫波函数是指形如 的波函数
的波函数 。其中
。其中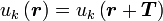 具有晶格周期性(
具有晶格周期性( 为晶格平移矢量)。
为晶格平移矢量)。布洛赫本人证明,对于上述的含周期势场的薛定谔方程,其解必为布洛赫波函数的形式。这一定理被称之为布洛赫定理。它表明,对于周期势场中的波动方程而言,其本征函数的形式为一个平面波
 乘以一个周期性函数
乘以一个周期性函数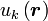 。
。布洛赫函数可以表示为行波波包的叠加,由于德布罗意提出电子可以表示为波,从而布洛赫波函数可以表示在离子实周期性势场中自由传播的电子。
[编辑] 紧束缚近似
紧束缚近似是将在一个原子附近的电子看作受该原子势场的作用为主,其他原子势场的作用看作微扰,从而可以得到电子的原子能级和晶体中能带之间的相互关系。在此近似中,能带的电子波函数可以写成布洛赫波函数之和的形式:
其中
 被称为瓦尼尔函数。
被称为瓦尼尔函数。可以用微扰理论求解该近似模型。求解结果为一个原子能级对应一条能带。紧束缚适用于计算相当多的晶体能带

![\left[-\frac{\hbar ^2}{2m} \nabla ^2 +V \left( r \right) \right] \psi = \mathcal E \psi](http://upload.wikimedia.org/math/b/d/c/bdc0cb0c26a11874a7c843e670af0ad7.png)
No comments:
Post a Comment