维基百科,自由的百科全书
重力波相當微弱,我們所預期在地球上可觀測到的最強引力波會來自很遠且古老的事件,在這事件中大量的能量發生劇烈移動(例子包括兩顆中子星的對撞,或兩個極重的黑洞對撞)。這樣的波動會造成地球上各處相對距離的變動,但這些變動的數量級應該頂多只有10-21。以激光干涉引力波天文台(LIGO)的雙臂而言,這樣的變化小於一顆質子直徑的千分之一。這樣的案例應該可以指引出為什麼偵測重力波是十分困難的。
引力波的存在而且也真的無所不在,是廣義相對論中一項毫不模糊的預言。所有目前相互競爭而且被“認可”的重力理論(「認可」:與現前可得一切證據能達到相當準確度的相符)所預言的重力輻射特質即各有千秋;而原則上,這些預言有時候和廣義相對論所預言的相差甚遠。但很不幸地,現在要確認重力輻射的存在性就已相當具有挑戰性,更不用說要研究它的細節。
雖然重力輻射並未被清楚地“直接”測到,然而已有顯著的“間接”證據支持它的存在。最著名的是天文學家對脈衝星雙星系統PSR B1913+16的觀測。這系統被認為具有兩顆中子星,以極其緊密而快速的模式互相環繞對方。其並且呈現了漸進式旋近(in-spiral),旋近時率恰好是廣義相對論所預期的值。對於這樣的觀測,最簡單(也幾乎是廣為接受)的解釋為:廣義相對論對準確說明系統的重力輻射。约瑟夫·泰勒和拉塞尔·赫尔斯因為這些成就共同获得了1993年诺贝尔物理学奖。
目录[隐藏] |
[编辑] 概觀
在愛因斯坦的廣義相對論裡,重力的本質是時空曲率的表現。約翰·惠勒所推廣的宣傳詞——「物質告訴時空如何彎曲,時空告訴物質如何運動。」——簡單傳神地表達出這項關係。舉例來說,若人站立着,可以感受到地面對足部的壓力。從廣義相對論的觀點,這表示與地面的接觸阻止了物體的自由下落,因而加速了物體。既然加速被視為對世界線的彎折,這表示非在自由下落的人體的世界線並不是短程線(測地線)。另一方面,時空若遠離任何質能則幾乎是完美平直。也因此,短程線表現上近似於較為人知的實體幾何學中的直線,因而小物體可以表現出直線慣性運動。廣義相對論以及其他類似的重力理論是以寫下場方程式來表達,有時可能另外也寫下運動方程式。也就是說,這些理論是古典相對論性場論,在這之中重力場或多或少都和時空曲率有關。因此某種程度上,一些區域的質能的快速運動會產生時空的漣漪,並向外輻射出,呈現為重力波。換個角度說,這是場的更新資訊從一處向另一處傳遞的表現。
相似於電磁輻射,在廣義相對論(以及其他競爭理論)中,重力輻射以光速前行,並且具有橫波的特性。橫波表示了重力波對於測試粒子運動的影響是發生在與傳播方向相垂直的平面。然而粗略來說:
- 重力波代表了一個二階張量場(矩陣)的微擾;在量子場論術語中會稱作是「自旋-2」。
- 電磁波則是來自於向量場的微擾;在量子場論中會稱作是「自旋-1」。
- 其他類型的物理學波動有很多來自於純量場的微擾;在量子場論中會稱作是「自旋-0」。
[编辑] 重力波源
[编辑] 偵測
[编辑] 「愛因斯坦在你家」重力波搜尋計畫(Einstein@Home)
Einstein@Home(意为“爱因斯坦在你家”),是一个由威斯康星大學密爾沃基分校主辦,基于BOINC计算平台的分布式计算项目。该项目計劃通过位于美国的激光干涉引力波天文台(Laser Interferometer Gravitational wave Observatory,LIGO)和位于德国的GEO 600引力波天文台收集数据,希望从这些收集来的数据当中寻找能够证实爱因斯坦的广义相对论中的引力波存在的证据。Einstein@Home 项目基于 BOINC 平台,设计目的是利用志愿计算的威力来处理分析 LIGO 和 GEO600 采集的海量观测数据,以从中寻找引力波存在的证据。该项目由 威斯康新-密尔沃基大学的 Bruce Allen 教授领导,在美国物理协会(APS)的支持下,作为“2005 世界物理年”的活动项目于 2005 年 2 月开始正式运行,现已成为 BOINC 平台的主要项目之一,目前项目正在对 LIGO 探测器首次运行在设计精度上所探测到的数据进行处理。
此外,Einstein@Home 于 2009 年 3 月正式启动了一个新的子项目,其目的主要是从阿雷西博天文台采集到的射电数据中寻找之前未发现过的脉冲星,关于该子项目的详细情况请看 en:Arecibo Binary Pulsar Search。
[编辑] 展望
| 未解決的物理學問題: 我們宇宙是否充滿始於大爆炸的重力輻射?又或是源於天文物理的客體,例如旋近的中子星?這些現象對於量子重力與廣義相對論方面,能夠告訴我們些什麼呢? |
[编辑] 推導
[编辑] 平直時空的微擾
考慮近乎平直的完整度規 ,而寫成平直度規
,而寫成平直度規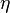 加上一些微擾
加上一些微擾 。
。 是里奇曲率。我們將對
是里奇曲率。我們將對 就
就 的冪級做微擾式的展開。
的冪級做微擾式的展開。 是對於平直芮奇曲率(因此是零)的偏離,其和微擾
是對於平直芮奇曲率(因此是零)的偏離,其和微擾 呈線性關係。
呈線性關係。現在我們要用到芮奇曲率的式子:
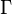 是克里斯托菲尔符號,而
是克里斯托菲尔符號,而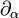 是
是 的簡略形。只有前兩項會對一階修正有貢獻,此二在
的簡略形。只有前兩項會對一階修正有貢獻,此二在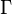 中是線性的:
中是線性的: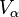 代表
代表 ,而
,而 是達朗貝爾算符(d'Alembertian)或4-拉普拉斯算符。升降指標可以是很具技巧性的。到第一階,你只需要用到平直度規。此外注意到反度規(inverse metric)帶有負的微擾加上其高階項。
是達朗貝爾算符(d'Alembertian)或4-拉普拉斯算符。升降指標可以是很具技巧性的。到第一階,你只需要用到平直度規。此外注意到反度規(inverse metric)帶有負的微擾加上其高階項。接著,我們挑選了一個特別的座標系統,其中
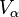 恰是零。要能如此需做一些證明,不過事實上真的可以。我們得到一條波動方程式與我們的規範條件(gauge condition)。
恰是零。要能如此需做一些證明,不過事實上真的可以。我們得到一條波動方程式與我們的規範條件(gauge condition)。 ,是個零向量。波動方程式現在被滿足了,不過
,是個零向量。波動方程式現在被滿足了,不過 該選什麼才能滿足我們所用的規範條件呢? 将:
該選什麼才能滿足我們所用的規範條件呢? 将: 代入
代入 ,且是橫波:
,且是橫波: 。
。對於一個沿
 方向前行的波,
方向前行的波, ,微擾會是如下形式:
,微擾會是如下形式:
因此振動會是橫向的空間扭曲。這樣的波稱為自旋-2因為存在有2個不同的偏振。光只有1!
 稱為加號偏振(plus polarization)而
稱為加號偏振(plus polarization)而 稱為叉號偏振(cross polarization)。
稱為叉號偏振(cross polarization)。[编辑] 有源微擾
愛因斯坦方程式描述了時空曲率與造成曲率的物質或源之間的關係: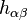 的散度。自此以後,對角元素反轉的微擾將簡化為
的散度。自此以後,對角元素反轉的微擾將簡化為 。
。我們現在可以將這些方程式併入線性化愛因斯坦方程式:
 是遲滯時間(retarded time)。
是遲滯時間(retarded time)。[编辑] 遠源的近似
如果想研究遠離波源的擾動的話,我們可以援引出一個非常有用的近似式: 代表距波源的近似值。
代表距波源的近似值。我们现在援引局部動量守恒原理,以找到应力张量之間有用的相互关系。
 的平方,以將兩部分融合,并得到一個正則積分式。
的平方,以將兩部分融合,并得到一個正則積分式。 是质量密度而
是质量密度而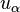 是四维速度。如果源是非相对论性的,则对能量密度有主要贡献的是质量密度,
是四维速度。如果源是非相对论性的,则对能量密度有主要贡献的是质量密度,
[编辑] 微擾法 對 精確解
重力波和電磁波性質迥異,理由是電磁波可以精確地從麥克斯韋方程式推導出來。然而重力波,作為線性、自旋-2的波,常被看作僅僅是特定時空幾何的微擾罷了。換言之,現實中總是會有線性、自旋-1的電磁波,卻不存在有線性、自旋-2的重力波。雖說仍有波樣的擾動,但一般來講,一如廣義相對論中總會出現的,事物是非線性的。這也是重力子可能不存在的理由之一。[编辑] 重力波會傳遞能量
科學社群中有部分人一開始對於「重力波是否會如同電磁波一般可以傳遞能量」感到困惑,這樣的困惑來自於一項事實:重力波沒有局域能量密度——如此對於應力-能量張量的量值不會造成貢獻。不像牛頓重力,愛因斯坦重力不是一項力理論。重力在廣義相對論中不是一種力,它是幾何。因此這樣的場原來被認為不含能量,一如重力勢。然而這場確實可以攜帶能量,如同它可以在遠處作出機械功。而這已經用可傳輸能量的應力-能量偽張量進行證明過,也可看出輻射是如何將能量往外攜帶到無限遠處。[编辑] 其他观点
新近的研究表明,引力波可能与电磁波有着相同的本质:宇宙背景辐射中的21厘米微波即是宇宙中氢原子辐射的引力波。这项理论和实验研究的结论与人们关于引力波的传统观念完全不同。[1][编辑] 参考资料
- ^ "Quantum resonance scheme to measure the gravitational constant G" Retrieved 2013-02-20.
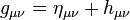






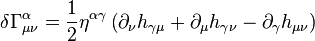

















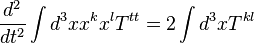




No comments:
Post a Comment