https://zh.wikipedia.org/wiki/%E5%A4%9A%E6%A5%B5%E5%B1%95%E9%96%8B
多極展開[编辑]
维基百科,自由的百科全书
在物理學裏,多極展開(multipole expansion)方法廣泛應用於涉及於質量分佈產生的重力場、電荷分佈產生的電勢或電場、電流分佈產生的磁向量勢和磁場、電磁波的傳播等等問題。使用多極展開,重力場或電勢等等,都可以表達為單極項目、偶極項目、四極項目、八極項目等等的疊加。一個典型範例是,從原子核的外部多極矩與電子軌域的內部多極矩之間的交互作用能量,計算求得原子的原子核外多極矩。由於從原子核的外多極矩可以給出原子核內部的電荷分佈,物理學者可以研究原子核的形狀。
做理論運算時,在允許誤差範圍內,時常可以只取多極展開的最低階的幾個非零項目,忽略其它項目,因為它們的數值超小。
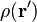 ,則其產生的電勢
,則其產生的電勢 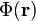 為
為
 是場位置,
是場位置, 是源位置,
是源位置,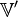 是積分的體積區域。
是積分的體積區域。
假設體積區域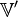 是在以原點為圓心、半徑為
是在以原點為圓心、半徑為  的圓球內部,則在圓球以外,電勢
的圓球內部,則在圓球以外,電勢 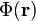 可以多極展開。文獻裏常見到兩種電勢的多極展開方法。一種展開為直角坐標
可以多極展開。文獻裏常見到兩種電勢的多極展開方法。一種展開為直角坐標 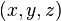 的泰勒級數,稱為「笛卡兒多極展開」(Cartesian multipole expansion);另一種是用距離倒數的冪和球諧函數展開,是以球坐標表示,稱為「球多極展開」(spherical multipole expansion)。
的泰勒級數,稱為「笛卡兒多極展開」(Cartesian multipole expansion);另一種是用距離倒數的冪和球諧函數展開,是以球坐標表示,稱為「球多極展開」(spherical multipole expansion)。
 在原點
在原點  的泰勒級數為
的泰勒級數為
 是對於
是對於  的偏微分。
的偏微分。
設定 ,則
,則  對於
對於  的偏微分為
的偏微分為
 是狄拉克δ函數。
是狄拉克δ函數。
所以 在原點
在原點  的泰勒級數為
的泰勒級數為
 、電偶極矩
、電偶極矩  、電四極矩(electric quadrupole moment)
、電四極矩(electric quadrupole moment)  分別以方程式定義為[1]
分別以方程式定義為[1]
 ,可以用球諧函數
,可以用球諧函數  展開為[1]
展開為[1]
 與
與  的球坐標分別為
的球坐標分別為 與
與 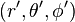 。
。
將這展開式代入電勢的方程式,則可得到
 以方程式定義為
以方程式定義為
 。以下列出幾個最低階的球多極矩的表達式,以及與笛卡兒多極矩之間的關係[1]:
。以下列出幾個最低階的球多極矩的表達式,以及與笛卡兒多極矩之間的關係[1]:
 ,笛卡兒多極展開會得到
,笛卡兒多極展開會得到  個笛卡兒多極矩,而球多極展開會得到
個笛卡兒多極矩,而球多極展開會得到 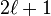 個球多極矩。這是因為兩種展開各自具有不同的旋轉變換屬性。笛卡兒多極矩是可約的(reducible);而球多極矩則是不可約的,這種分解能夠得到旋轉群的不可約表示。
個球多極矩。這是因為兩種展開各自具有不同的旋轉變換屬性。笛卡兒多極矩是可約的(reducible);而球多極矩則是不可約的,這種分解能夠得到旋轉群的不可約表示。
在多極展開式裏,不等於零的最低階多極矩,其數值與原點的選擇無關。例如,對於在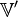 內部、位置為
內部、位置為  的單獨點電荷,電荷密度可以寫為
的單獨點電荷,電荷密度可以寫為  。這單獨點電荷的電單極矩為
。這單獨點電荷的電單極矩為  ,與原點位置無關。
,與原點位置無關。
對於在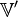 內部、位置分別為
內部、位置分別為  、
、 的兩個異電性、同電量的點電荷,電荷密度可以寫為
的兩個異電性、同電量的點電荷,電荷密度可以寫為 ![\rho(\mathbf{r}')=q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]](https://upload.wikimedia.org/math/1/4/3/14311a67654d1bc1e98e20d17f8076ca.png) 。這單獨點電荷的電單極矩為
。這單獨點電荷的電單極矩為 ![\int_{\mathbb{V'}}q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]\ \mathrm{d}^3\mathbf{r}' =0](https://upload.wikimedia.org/math/e/9/5/e95426553a1b518ad0ad057dc1294654.png) 。最低階多極矩為電偶極矩
。最低階多極矩為電偶極矩 ![\int_{\mathbb{V'}}\mathbf{r}'q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]\ \mathrm{d}^3\mathbf{r}' =q(\mathbf{r}'_1-\mathbf{r}'_2)](https://upload.wikimedia.org/math/0/4/a/04a14cbd70fc17d275be1e4b287cb47d.png) 。這電偶極矩與原點位置無關,與兩個點電荷之間的相對位置有關。
。這電偶極矩與原點位置無關,與兩個點電荷之間的相對位置有關。
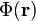 的電荷密度分佈
的電荷密度分佈 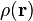 ,則其電能
,則其電能  為
為
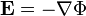 ,外電勢
,外電勢 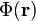 在原點
在原點  的泰勒級數為
的泰勒級數為
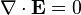 ,電勢可以寫為
,電勢可以寫為
 ,則其產生的磁向量勢
,則其產生的磁向量勢  為
為
 是場位置,
是場位置, 是源位置。
是源位置。
將前面推導出的 在原點
在原點  的泰勒級數帶入磁向量勢方程式,則可得到
的泰勒級數帶入磁向量勢方程式,則可得到
 ,
,
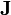 是局部的,假若積分體積
是局部的,假若積分體積  足夠大,則位於包含積分體積的曲面
足夠大,則位於包含積分體積的曲面  的電流密度分佈為零:
的電流密度分佈為零:
 等於零。
等於零。
磁偶極子項目不等於零。首先,應用高斯散度定理和電流密度分佈的局部性這事實,可以得到
 為
為
 為
為
做理論運算時,在允許誤差範圍內,時常可以只取多極展開的最低階的幾個非零項目,忽略其它項目,因為它們的數值超小。
目录[隐藏] |
電勢的多極展開式[编辑]
在靜電學裏,設定電荷密度分佈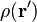 ,則其產生的電勢
,則其產生的電勢 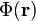 為
為 ;
;
 是場位置,
是場位置, 是源位置,
是源位置,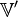 是積分的體積區域。
是積分的體積區域。假設體積區域
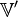 是在以原點為圓心、半徑為
是在以原點為圓心、半徑為  的圓球內部,則在圓球以外,電勢
的圓球內部,則在圓球以外,電勢 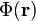 可以多極展開。文獻裏常見到兩種電勢的多極展開方法。一種展開為直角坐標
可以多極展開。文獻裏常見到兩種電勢的多極展開方法。一種展開為直角坐標 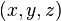 的泰勒級數,稱為「笛卡兒多極展開」(Cartesian multipole expansion);另一種是用距離倒數的冪和球諧函數展開,是以球坐標表示,稱為「球多極展開」(spherical multipole expansion)。
的泰勒級數,稱為「笛卡兒多極展開」(Cartesian multipole expansion);另一種是用距離倒數的冪和球諧函數展開,是以球坐標表示,稱為「球多極展開」(spherical multipole expansion)。笛卡兒多極展開[编辑]
任意函數 在原點
在原點  的泰勒級數為
的泰勒級數為 ;
;
 是對於
是對於  的偏微分。
的偏微分。設定
 ,則
,則  對於
對於  的偏微分為
的偏微分為 、
、 ;
;
 是狄拉克δ函數。
是狄拉克δ函數。所以
 在原點
在原點  的泰勒級數為
的泰勒級數為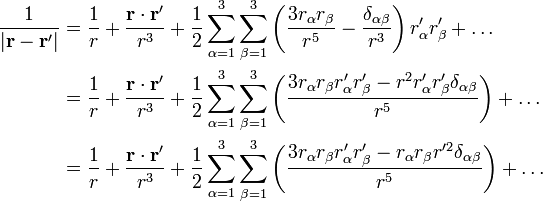 。
。
![\Phi(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\int_{\mathbb{V'}}
\left[\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}
+\frac{1}{2}\sum_{\alpha=1}^3\sum_{\beta=1}^3 \frac{r_\alpha r_\beta (3 r'_\alpha r'_\beta - r^{\prime 2}\delta_{\alpha\beta})}{r^5}+\dots\right] \rho(\mathbf{r}')\ \mathrm{d}^3\mathbf{r}'](https://upload.wikimedia.org/math/c/8/6/c86cfc8fa87fcfcbac1d75e328e996a8.png) 。
。
 、電偶極矩
、電偶極矩  、電四極矩(electric quadrupole moment)
、電四極矩(electric quadrupole moment)  分別以方程式定義為[1]
分別以方程式定義為[1] 、
、 、
、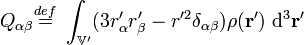 。
。
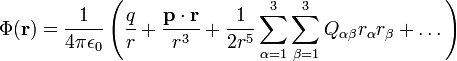 。
。
球多極展開[编辑]
場位置與源位置之間距離的倒數, ,可以用球諧函數
,可以用球諧函數  展開為[1]
展開為[1]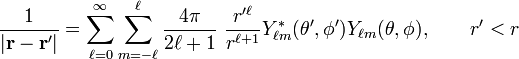 ;
;
 與
與  的球坐標分別為
的球坐標分別為 與
與 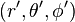 。
。將這展開式代入電勢的方程式,則可得到
 。
。
 以方程式定義為
以方程式定義為 。
。
 。
。
 。以下列出幾個最低階的球多極矩的表達式,以及與笛卡兒多極矩之間的關係[1]:
。以下列出幾個最低階的球多極矩的表達式,以及與笛卡兒多極矩之間的關係[1]: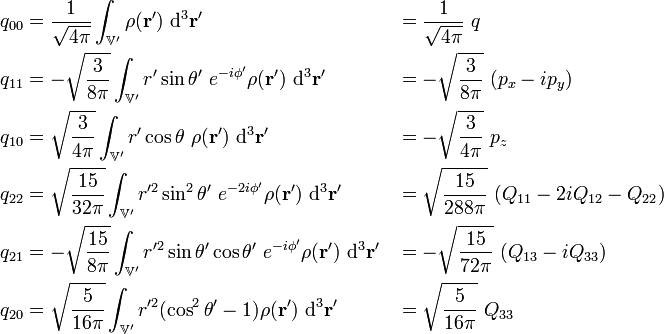 。
。
多極展開式的特性[编辑]
對於多極展開式的每一階 ,笛卡兒多極展開會得到
,笛卡兒多極展開會得到  個笛卡兒多極矩,而球多極展開會得到
個笛卡兒多極矩,而球多極展開會得到 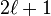 個球多極矩。這是因為兩種展開各自具有不同的旋轉變換屬性。笛卡兒多極矩是可約的(reducible);而球多極矩則是不可約的,這種分解能夠得到旋轉群的不可約表示。
個球多極矩。這是因為兩種展開各自具有不同的旋轉變換屬性。笛卡兒多極矩是可約的(reducible);而球多極矩則是不可約的,這種分解能夠得到旋轉群的不可約表示。在多極展開式裏,不等於零的最低階多極矩,其數值與原點的選擇無關。例如,對於在
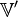 內部、位置為
內部、位置為  的單獨點電荷,電荷密度可以寫為
的單獨點電荷,電荷密度可以寫為  。這單獨點電荷的電單極矩為
。這單獨點電荷的電單極矩為  ,與原點位置無關。
,與原點位置無關。對於在
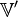 內部、位置分別為
內部、位置分別為  、
、 的兩個異電性、同電量的點電荷,電荷密度可以寫為
的兩個異電性、同電量的點電荷,電荷密度可以寫為 ![\rho(\mathbf{r}')=q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]](https://upload.wikimedia.org/math/1/4/3/14311a67654d1bc1e98e20d17f8076ca.png) 。這單獨點電荷的電單極矩為
。這單獨點電荷的電單極矩為 ![\int_{\mathbb{V'}}q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]\ \mathrm{d}^3\mathbf{r}' =0](https://upload.wikimedia.org/math/e/9/5/e95426553a1b518ad0ad057dc1294654.png) 。最低階多極矩為電偶極矩
。最低階多極矩為電偶極矩 ![\int_{\mathbb{V'}}\mathbf{r}'q[\delta(\mathbf{r}'-\mathbf{r}'_1)-\delta(\mathbf{r}'-\mathbf{r}'_2)]\ \mathrm{d}^3\mathbf{r}' =q(\mathbf{r}'_1-\mathbf{r}'_2)](https://upload.wikimedia.org/math/0/4/a/04a14cbd70fc17d275be1e4b287cb47d.png) 。這電偶極矩與原點位置無關,與兩個點電荷之間的相對位置有關。
。這電偶極矩與原點位置無關,與兩個點電荷之間的相對位置有關。電能的多極展開式[编辑]
假設處於外電勢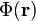 的電荷密度分佈
的電荷密度分佈 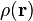 ,則其電能
,則其電能  為
為 。
。
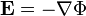 ,外電勢
,外電勢 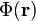 在原點
在原點  的泰勒級數為
的泰勒級數為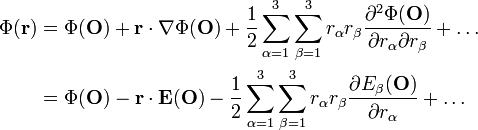 。
。
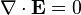 ,電勢可以寫為
,電勢可以寫為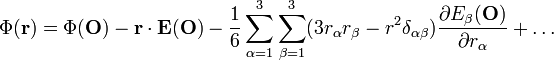 。
。
 。
。
磁向量勢的多極展開式[编辑]
在靜磁學裏,設定電流密度分佈 ,則其產生的磁向量勢
,則其產生的磁向量勢  為
為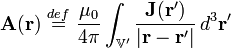 ;
;
 是場位置,
是場位置, 是源位置。
是源位置。將前面推導出的
 在原點
在原點  的泰勒級數帶入磁向量勢方程式,則可得到
的泰勒級數帶入磁向量勢方程式,則可得到![\mathbf{A}(\mathbf{r})=\frac{\mu_0}{4\pi}\int_{\mathbb{V'}}
\left[\frac{1}{r}+\frac{\mathbf{r}\cdot\mathbf{r}'}{r^3}
+\frac{1}{2}\sum_{\alpha=1}^3\sum_{\beta=1}^3 \frac{r_\alpha r_\beta (3 r'_\alpha r'_\beta - r^{\prime 2}\delta_{\alpha\beta})}{r^5}+\dots\right] \mathbf{J}(\mathbf{r}')\ \mathrm{d}^3\mathbf{r}'](https://upload.wikimedia.org/math/6/5/5/655a9719b5fc0390286e0f216f2b4409.png) 。
。
 ,
,![\begin{align}\int_{\mathbb{V}'}J_{\alpha}(\mathbf{r}')\, d^3\mathbf{r}' & =\int_{\mathbb{V}'}[\mathbf{J}(\mathbf{r}')\cdot\nabla']r'_{\alpha}\, d^3\mathbf{r}'
=\int_{\mathbb{V}'}\nabla'\cdot[r'_{\alpha}\mathbf{J}(\mathbf{r}')]-r'_{\alpha}\nabla'\cdot\mathbf{J}(\mathbf{r}')\, d^3\mathbf{r}' \\
& =\int_{\mathbb{V}'}\nabla'\cdot[r'_{\alpha}\mathbf{J}(\mathbf{r}')]\, d^3\mathbf{r}' \\
\end{align}](https://upload.wikimedia.org/math/5/0/1/501ac616d4ea5c30aafbe847bead043d.png) ;
;
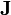 是局部的,假若積分體積
是局部的,假若積分體積  足夠大,則位於包含積分體積的曲面
足夠大,則位於包含積分體積的曲面  的電流密度分佈為零:
的電流密度分佈為零: 。
。
 等於零。
等於零。磁偶極子項目不等於零。首先,應用高斯散度定理和電流密度分佈的局部性這事實,可以得到
![\begin{align}
\int_{\mathbb{V}'}\nabla'\cdot[r'_{\alpha}r'_{\beta}J(\mathbf{r}')]\, d^3\mathbf{r}' &
=\int_{\mathbb{V}'}r'_{\beta}[J(\mathbf{r}')\cdot\nabla']r'_{\alpha}
+r'_{\alpha}[J(\mathbf{r}')\cdot\nabla']r'_{\beta}
+r'_{\alpha}r'_{\beta}\nabla'\cdot J(\mathbf{r}')\, d^3\mathbf{r}' \\
& =\int_{\mathbb{V}'}r'_{\beta}J_{\alpha}(\mathbf{r}')+r'_{\alpha}J_{\beta}(\mathbf{r}')\, d^3\mathbf{r}' \\
& = 0 \\
\end{align}](https://upload.wikimedia.org/math/0/6/b/06b8317e2ac27712066758407781fe12.png) 。
。
![\begin{align}
\mathbf{r}\cdot\int_{\mathbb{V'}}\mathbf{r}'J_{\alpha}(\mathbf{r}')\ \mathrm{d}^3\mathbf{r}'
& = \frac{1}{2}\sum_{\beta=1}^3 r_{\beta}\int_{\mathbb{V'}}r'_{\beta}J_{\alpha}(\mathbf{r}')-r'_{\alpha}J_{\beta}(\mathbf{r}')\ \mathrm{d}^3\mathbf{r}' \\
& = -\ \frac{1}{2}\left[\mathbf{r}\times\int_{\mathbb{V'}}
\mathbf{r}'\times\mathbf{J}(\mathbf{r})\ \mathrm{d}^3\mathbf{r}'\right]_{\alpha} \\
\end{align}](https://upload.wikimedia.org/math/7/1/2/712e1adeabf0cb990c24be9dba07e86d.png) 。
。
 為
為 。
。
 為
為 。
。

No comments:
Post a Comment