【2012諾貝爾】個別量子系統的測量與操縱
■ 今年的諾貝爾物理獎，頒發給可讓科學家對個別量子系統進行測量與操縱的實驗性發明與發現。這可分為兩個各自獨立，但卻彼此相關的科技：一是用和諧阱困住離子，二是用空腔困住光子。
編譯│高英哲
簡介
量子力學描述構成我們這個世界的個別成分，也就是原子（物質）跟光子（光線）的行為。這些粒子很少單獨存在，通常跟它們的周遭環境有著很密切的互動關係。一團粒子的行為通常會跟個別粒子有所不同，一般都能透過古典物理學加以描述。然而在量子力學的領域裡，物理學家卻會利用想像出來的實驗環境，把情況加以簡化，藉此預測單一量子粒子的行為。
在一九八〇年代跟一九九〇年代，物理學家發明了把困在離子阱裡的個別離子冷卻下來，透過雷射光的幫助控制其狀態的方法。藉由跟環境只有最低程度互動的光子，個別離子如今可以在「原位」 (in situ) 進行操控與觀察。在另一種類型的實驗中，可將光子困在空腔內加以操控。在精心設計的實驗操作下，可以觀察這些被困住的光子，而不至於使它們因為跟原子產生互動而被摧毀。這些技法使得科學家身先士卒，開始研究測試量子力學的基本原理，以及宏觀與微觀世界之間轉換的過程，而且不再局限於想像中的實驗，而是得以實際操作加以驗證。這些研究促成了量子運算研究領域的發展，也從而產生新一代的高精確度光學鐘。
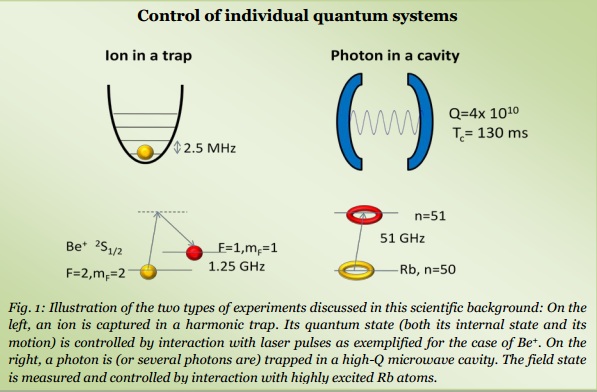
今年的諾貝爾物理獎，頒發給可讓科學家對個別量子系統進行測量與操縱的實驗性發明與發現。這可分為兩個各自獨立，但卻彼此相關的科技：一是用和諧阱困住離子，二是用空腔困住光子（見圖一）。此次諾貝爾獎科學背景的兩種實驗圖解：左邊是一個離子被困在一個和諧阱中，其量子態（內部態及其運動皆然）就如同圖例中的鈹離子所示，受到與雷射脈衝的互動所控制。右邊則是一個或好幾個光子被困在高 Q 度的微波空腔內，微波場態是透過與高度激化的銣原子的互動，加以測量與控制。
這兩者之間有幾個有趣的相似之處。在這兩種情況下，量子態都是透過與量子化諧振子耦合的雙能階系統，以非破壞性的量子測量法加以觀察，所謂的傑恩斯—康明斯漢密爾頓量 (Jaynes-Cummings Hamiltonian) 就是在描述這種狀況。雙能階系統由一個離子（帶有兩個與雷射光耦合的能階）或一個高度激化的原子（帶有兩個與微波場耦合的雷德堡 (Rydberg) 能階）所構成。量子化諧振子則是在描述困在阱裡的離子運動，或是困在空腔裡的微波場。
在簡短的背景介紹後，我們在此描述這兩種情況各自的實施做法，並提出一些重要的科技應用。
困住離子法
這個研究領域是從一九七〇年代研發出來，用來困住充電粒子的技法開始發展起來的。一九八九年的諾貝爾物理獎得主鮑爾 (Paul) 跟德梅特 (Dehmelt) ，就是因為他們「研發出困住離子的技法」而得獎。由洪許 (Hänsch) 跟夏洛 (Schawlow) 在一九七五年提出的中性原子都卜勒 (Doppler) 冷卻法，以及懷蘭德 (Windland) 跟德梅特在同年提出的離子都卜勒冷卻法，是控制個別
獨立離子相當重要的一個進展。懷蘭德跟紐豪瑟 (Neuhauser) 等人在一九七八年，各自對鎂離子 (Mg+) 跟鋇離子 (Ba+) 進行困住離子的第一次實驗。懷蘭德、艾克斯壯 (Ekstrom) 跟德梅特早在一九七三年，就在探討捕捉單一離子的可能性。到了一九八〇年，托謝克 (Toschek) 領導的研究團隊就在鮑爾設計的離子阱裡，成功捕捉到單一的鋇離子；懷蘭德跟伊塔諾 (Itano) 則在一九八一年，用潘寧 (Penning) 設計的離子阱捕捉到一個鎂離子。由佩爾 (Peil) 跟加布瑞瑟 (Gabrielse) 領導的研究團隊，則在一九九九年研發出與此有密切關係的技法，用來冷卻潘寧阱裡捕捉到的單一電子。
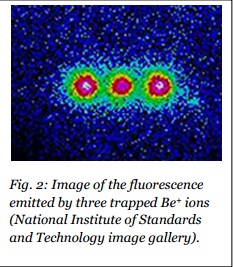
離子阱是在超高度的真空中，結合靜電場與振盪電場所製造出來的。離子阱有只會捕捉到一個離子的，也有好幾個離子會成一條線分佈的線性阱。被困住的離子具有振盪運動，在低溫下會量子化，因此離子會帶有兩套量子化能階：描述在阱中運動的振動模式（又稱外部態），以及描述離子內部量子態的電子能階。這些能階可用吸光或發光現象，或是透過一種叫做「拉曼躍遷」 (Raman transition) 的雙光子過程加以耦合。透過用雷射激發強烈散射光的光學躍遷，這些離子便可直接用肉眼或是 CCD 攝影機（見圖二）加以觀察。此外，離子的內部態也能藉由觀察量子跳躍加以判定，納葛尼 (Nagourney) 等人跟懷蘭德、伯格奎斯特 (Bergquist) 等人在一九八六年，就分別示範過要怎麼做了。
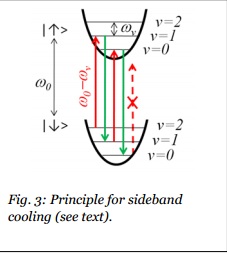
要控制離子的量子態有一步很重要，就是要利用一種叫做「側帶冷卻」 (sideband cooling) 的技法，把離子阱降溫到能量最低的狀態，迪崔奇 (Diedrich) 等人在一九八九年，以及門羅 (Monroe) 等人在一九九五年，都曾經探討過這個技法。圖三顯示離子阱裡的離子，在兩種不同的電子能階下的幾種振動狀態（|↓> 跟 |↑>）。這套技法會激化離子，增加內部能量並減低振動能量。要達到這些效果，就要用一道頻率為 ω0 – ων 的窄頻雷射， ων 代表離子阱兩種振盪模式之間的頻率區間，而ω0 則是原子頻率，也就是該離子兩種電子能階之間的頻率差。受激化的離子會優先往具有同樣振動量子數ν 的狀態產生衰變。這套由懷蘭德等人研發出來的技法，可以控制離子的內部與外部自由度。在確實監控離子阱特質的情況下，就能創造出ν 定義得很清楚的運動福克態 (Fock state) ，以及各種受到良好控制的重疊福克態，比方說同調態或熱力態。米克霍夫 (Meekhof) 等人在一九九六年對此有論文加以探討。
另外一大突破則是發展出將電子態的量子重疊，轉變為離子阱振動模式的量子重疊技法。席哈克 (Cirac) 跟左勒 (Zoller) 在一九九五年提出理論做法，門羅等人在同年就把實作技法研究出來。經過這個技法轉變的量子重疊，就能夠轉移到另一個跟第一個離子具有相同振動態的離子上面，奧地利因斯布魯克大學的布拉特 (Blatt) 跟史密特卡勒 (Schmidt-Kaler) 等人，在二〇〇三年展示了如何做到這點。這套技法廣泛使用在有用到超導迴路的研究工作上，薛可夫 (Schoelkopf) 跟紀爾文 (Girvin) 在二〇〇八年發表的論文中，將這套技法取名為「迴路QED」 (Circuit-QED) 。
小欄一：創造、移轉離子的重疊態
想像有一個被困在阱裡的離子，最低電子態為 |↓> ，最低阱態為 |0> 。這個量子系統可以用下列式子表示：
|φ0> = |↓>|0>.
這個離子可用雷射脈衝加以激化，從而創造出一個同調重疊態：
|φ0>→|φ1> = (α|↓> + β|↑>) |0>.
「紅側帶」π-puls （頻率等於ω0 – ων ，見圖三）與離子產生交互作用。由於離子處在最低振動模式，只有 |↑>|0> 狀態會受到影響。離子躍遷到 |↓>|1> ，因此
|φ1>→|φ2> = α|↓> |0> + β|↓>|1> = |↓> (α|0>+β|1>).
重疊態就這樣移轉到離子的振動模式。倘若阱中還含有另一個離子，該離子會跟第一個離子具有相同的振動模式。如此一來重疊態就能夠以同樣的方式，移轉到第二個離子的內部態。
微波空腔則是哈羅契 (Haroche) 、雷蒙 (Raimond) 跟布魯恩 (Brune) 等人所用的主要實驗組件。微波空腔由兩塊相隔 2.7 公分的球面鏡構成，鏡子是由超導材質鈮 (Nb) 製成，並且冷卻到非常低的 0.8K 溫度。製作鏡面的技術品質在大約十年前大幅提升，使得空腔能夠有可達到 4×1010 的極高 Q 值，也就是說光子在空腔內能夠維持非常長的一段時間（大約 130 毫秒）。在這樣的空腔內，光子在消失前可以行進大約40,000公里。
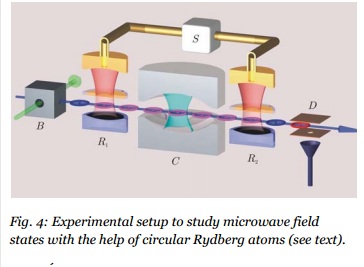
空腔內的場可用在圓形雷德堡態（比方說 n = 50, l = |m|=49 ）的銣 (Rb) 原子加以探測。有些原子的範圍很大，半徑長達 125 奈米，與空腔內的場耦合性非常強。從n = 50 (|↓>) 躍遷到 n = 51 (|↑>) ，其頻率幾乎跟空腔內的微波場相同 (51 GHz) 。 R1 跟 R2 兩個空腔是用來創造介於 |↓> 跟 |↑> 之間受控制的量子重疊，並且加以分析。有個選擇性的場離子化偵測器 (D) ，是用來偵測原子狀態的。由同調來源製造出來的光子，透過波導管與空腔耦合。原子一次一個，以控制下的速度送進空腔裡，因此產生交互作用的時間也能受到控制。在哈羅契的研究團隊所進行的大多數實驗中，原子跟場的頻率有些微差異。在空腔內行進的原子並不會吸收光子，其能階反而會因為動態史塔克效應 (Stark effect) 而產生位移，微波場的相位變異也包括在內。這個相位位移的符號相反，要看這個原子是在 |↓> 還是 |↑> 的狀態而定，導致原子態與場態纏結（詳見布魯恩等人在一九九六年發表的論文）。
哈羅契等人在一九九〇年，提出一個以非破壞性量子測量法，測量空腔內光子數量的方法（詳見布魯恩等人同年發表的論文）。葛利澤斯 (Gleyzes) 等人在二〇〇七年用實驗展示實作方法，相關實驗亦可參考諾格斯 (Nogues) 等人在一九九九年的研究成果。他們在空腔中捕捉到個別的光子，並且透過它們與原子的互動加以觀察。關於這種測量方式的原理，在小欄二裡有更詳細的解說。由於有這種測量法，就產生了波函數的「漸進崩解」 (progressive collapse) ，可透過非破壞性量子測量法加以觀察的實驗。在這些實驗中，光子的數量在量測過程中即使有所增減，也可追蹤無誤（詳見古爾林 (Guerlin) 等人在二〇〇七年發表的論文）。
小欄二：如何測量空腔內的光子而不使其摧毀
一個在 |↑> 狀態的原子在 B 的位子準備就緒（見圖四）。在 R1 有一股π/2 的脈衝，創造出 |↓> 跟 |↑> 原子態的重疊態，因此 |φ1> = (|↓> + |↑>)/√2.
重疊態在行經空腔 C 之後，就會變成 |φ> = (|↓> + eiφ |↑>)/√2 ，φ是原子態的重疊態在行經過程中累積的相位。由原子態的重疊態創造出來的原子雙極，其作用就像個時鐘一樣，而行經空腔過後的相位，就代表時鐘的指針位置。空腔內的微波場頻率與原子頻率略有出入。橫越空腔的原子並不會吸收或釋放光子，然而其能階卻會隨著產生位移，結果是相位 φ 會按照空腔內的光子數目而有所改變。
原子的行經時間是可以選定的，所以倘若空腔內沒有光子的話，φ = 0 mod 2π 。當原子抵達 R2 時，原子已位於重疊態 |φ1> 。原子在 R2 與另一道 π/2 的脈衝產生交互作用，因此 |φ1>→ |↓> ，這個現象由 D 偵測到。原子頻率與空腔內微波場頻率的出入也是可以選定的，因此倘若空腔內有一個光子的話，φ = π 。當原子在跟一個光子產生互動，抵達 R2 之後，原子已位於重疊態 |φ2> = (|↓>– |↑>) /√2 。原子跟 π/2 脈衝產生互動時， |φ2>→|↑> 。因此無論空腔內有 0 個還是 1 個光子，我們都有可能以非破壞性的方式加以測量。這種測量方式可以延伸到有幾個光子的情況，只要利用不同的相位跟幾個原子，重複類似的測量方式即可。
以實驗探討「薛丁格的貓」
量子物理學的核心問題，就是在於量子與古典物理學之間要如何轉換。這個問題可用廣為流傳，叫做「薛丁格的貓」(Schrödinger’s cat) 的矛盾加以闡述。這個名稱是指薛丁格在一九三五年所提出的一個想像實驗，用來強調要把量子力學的概念應用到日常生活中有多困難（見圖五）。他提出的問題是：隨著時光流逝，一個量子系統要到什麼時候，才會從一個既有的重疊態變成另一個？自從量子力學在一九三〇年代產生以來，許多物理學家就一直在鑽研量子物理學與古典物理學的界限（詳見祖瑞克 (Zurek) 在一九九一年發表的論文，以及雷格特 (Leggett) 等人在一九八七年的文獻回顧）。
哈羅契跟懷蘭德等人所領導的研究團隊，對於單一量子系統做到的控制程度，使他們得以在實驗室裡，利用光子跟離子進行類似薛丁格的貓的實驗（詳見哈羅契在一九九八年寫的文獻回顧）。大衛多維奇 (Davidovich) 等人在一九九六年提出一個實驗設計，哈羅契的研究團隊隨即著手實作，把一個雷德堡原子跟空腔場纏結，藉此創造出一個類似薛丁格的貓的微波場態重疊。這樣的重疊非常脆弱，只要跟環境耦合便會輕易被摧毀（在這個例子中，指的是逃離空腔的光子）。這個重疊的脫散現象（也就是演變為一個統計上的混態）可以當成一個時間與重疊態特性函數來加以測量。懷蘭德等人利用離子阱技法，進行了類似的實驗，他們創造出跟運動同調態纏結的受困單一離子，用這些離子來構成「貓態」（詳見門羅等人在一九九六年發表的論文），並觀察其脫散現象（詳見彌亞特 (Myatt) 等人在二〇〇八年所做研究）。哈羅契等人最近創造出貓態，加以測量並且拍了一部影片，展示貓態如何從重疊態演變成古典混態（詳見戴樂葛利瑟 (Deléglise) 等人在二〇〇八年發表的論文）。這種超凡的控制程度，也使得他們得以做出量子回饋機制，對脫散效應進行測量並加以修正，從而「穩定」量子態，比方說使其穩定在一個給定的福克態（詳見賽林 (Sayrin) 等人在二〇一一年的研究成果）。
量子電腦
席哈克跟左勒在一九九五年發表了一篇極具影響力的理論性文章，指出可用被困住的離子建造一台量子電腦。我們可將量子位元 (qubits) 編碼到被困離子的超精細能階中，因為被困離子與環境的互動非常弱，因此保存時間就可拉長。藉由質心運動，兩個以上的離子都能夠加以耦合（如小欄一所示）。懷蘭德的研究團隊率先進行鈹離子 (Be+) 運動與旋轉的二量子位元（受控否閘 (CNOT) ）實驗（詳見門羅等人於一九九五年發表的論文），從那之後，以被困離子為基礎的量子資訊研究領域，就有了相當可觀的進展。奧地利因斯布魯克大學的布拉特等人，在二〇〇三年做到了用鈣離子 (Ca+) 進行 CNOT 運算（詳見史密特卡勒等人在當年的研究成果）。時至今日，最先進的量子電腦科技是根據被困離子做出來的，並且可運用多達 14 個量子位元，以及一系列的運算閘與運算協定（詳見布拉特與懷蘭德在二〇〇八年所寫的文獻回顧）。不過未來若要研發出運算能力能夠超越古典電腦之所及的大型裝置，則需要克服相當多的挑戰。
光學鐘
光學鐘是懷蘭德研究被困離子的一項重要應用。根據在可見光區域的離子躍遷做出來的光學鐘之所以有意思，是因為可見光或紫外線光的躍遷頻率，比起在無線電波範圍運作的銫原子鐘躍遷頻率，嘖嘖高出了好幾個數量級。懷蘭德等人研發出來的光學鐘（如迪達姆斯 (Diddams) 等人在二〇〇一年，羅森班德 (Rosenband) 等人在二〇〇八年，以及周清文等人在二〇一〇年所做的），目前的精確度剛好可達到10-17 以下，比目前銫原子鐘的頻率標準還要精確兩個數量級。
光學離子鐘靠的是對攝動不怎麼敏感的單一離子狹窄躍遷（又稱禁戒躍遷 (forbidden transition) ）。這離子也必須要具有強烈的容許躍遷 (allowed transition) ，才能夠有效地加以冷卻，供人偵測。懷蘭德等人研發出一種叫做「量子邏輯光譜分析」 (quantum logic spectroscopy) 的新技法，靠的是兩種離子的纏結狀態，如小欄一所示。使用這個技法時，其中一個離子提供光譜躍遷（比方說 1S0→3P1 在 27Al+ (267 奈米) ），另一個離子（比方說 9Be+）則有強烈的冷卻躍遷（詳見史密特 (Schmidt) 等人在二〇〇五年發表的論文）。兩個不同光學鐘的精確度，可以透過由洪許跟霍爾 (Hall) 發明的頻梳 (frequency comb) 技法進行比較，他們兩位藉此獲頒二〇〇五年諾貝爾物理獎。
最近光學鐘所達到的精確度，使懷蘭德等人得以測量相對論效應，比方說在時速幾千公里下的時間擴大現象，或是兩點間僅有大約 30 公分高度差時的重力勢能差（詳見周清文在二〇一〇年發表的論文）。
總結
懷蘭德與哈羅契發明了可以用高精確度，對個別量子系統進行測量與控制的新科技，並且實作成功。他們的研究成果使我們得以透過測量類似「薛丁格的貓」狀態的演變過程，來研究脫散現象，這對於開發量子電腦，研發極為精確的光學鐘，邁出了第一步。
–
編譯│高英哲
簡介
量子力學描述構成我們這個世界的個別成分，也就是原子（物質）跟光子（光線）的行為。這些粒子很少單獨存在，通常跟它們的周遭環境有著很密切的互動關係。一團粒子的行為通常會跟個別粒子有所不同，一般都能透過古典物理學加以描述。然而在量子力學的領域裡，物理學家卻會利用想像出來的實驗環境，把情況加以簡化，藉此預測單一量子粒子的行為。
在一九八〇年代跟一九九〇年代，物理學家發明了把困在離子阱裡的個別離子冷卻下來，透過雷射光的幫助控制其狀態的方法。藉由跟環境只有最低程度互動的光子，個別離子如今可以在「原位」 (in situ) 進行操控與觀察。在另一種類型的實驗中，可將光子困在空腔內加以操控。在精心設計的實驗操作下，可以觀察這些被困住的光子，而不至於使它們因為跟原子產生互動而被摧毀。這些技法使得科學家身先士卒，開始研究測試量子力學的基本原理，以及宏觀與微觀世界之間轉換的過程，而且不再局限於想像中的實驗，而是得以實際操作加以驗證。這些研究促成了量子運算研究領域的發展，也從而產生新一代的高精確度光學鐘。
圖一：控制個別量子系統。（左）阱中的離子 （右）空腔中的光子
這兩者之間有幾個有趣的相似之處。在這兩種情況下，量子態都是透過與量子化諧振子耦合的雙能階系統，以非破壞性的量子測量法加以觀察，所謂的傑恩斯—康明斯漢密爾頓量 (Jaynes-Cummings Hamiltonian) 就是在描述這種狀況。雙能階系統由一個離子（帶有兩個與雷射光耦合的能階）或一個高度激化的原子（帶有兩個與微波場耦合的雷德堡 (Rydberg) 能階）所構成。量子化諧振子則是在描述困在阱裡的離子運動，或是困在空腔裡的微波場。
在簡短的背景介紹後，我們在此描述這兩種情況各自的實施做法，並提出一些重要的科技應用。
困住離子法
這個研究領域是從一九七〇年代研發出來，用來困住充電粒子的技法開始發展起來的。一九八九年的諾貝爾物理獎得主鮑爾 (Paul) 跟德梅特 (Dehmelt) ，就是因為他們「研發出困住離子的技法」而得獎。由洪許 (Hänsch) 跟夏洛 (Schawlow) 在一九七五年提出的中性原子都卜勒 (Doppler) 冷卻法，以及懷蘭德 (Windland) 跟德梅特在同年提出的離子都卜勒冷卻法，是控制個別
圖二：三個被困的鈹離子所發出的螢光造影（美國國家標準技術局提供）。
離子阱是在超高度的真空中，結合靜電場與振盪電場所製造出來的。離子阱有只會捕捉到一個離子的，也有好幾個離子會成一條線分佈的線性阱。被困住的離子具有振盪運動，在低溫下會量子化，因此離子會帶有兩套量子化能階：描述在阱中運動的振動模式（又稱外部態），以及描述離子內部量子態的電子能階。這些能階可用吸光或發光現象，或是透過一種叫做「拉曼躍遷」 (Raman transition) 的雙光子過程加以耦合。透過用雷射激發強烈散射光的光學躍遷，這些離子便可直接用肉眼或是 CCD 攝影機（見圖二）加以觀察。此外，離子的內部態也能藉由觀察量子跳躍加以判定，納葛尼 (Nagourney) 等人跟懷蘭德、伯格奎斯特 (Bergquist) 等人在一九八六年，就分別示範過要怎麼做了。
圖三：側帶冷卻原理（見內文）。
另外一大突破則是發展出將電子態的量子重疊，轉變為離子阱振動模式的量子重疊技法。席哈克 (Cirac) 跟左勒 (Zoller) 在一九九五年提出理論做法，門羅等人在同年就把實作技法研究出來。經過這個技法轉變的量子重疊，就能夠轉移到另一個跟第一個離子具有相同振動態的離子上面，奧地利因斯布魯克大學的布拉特 (Blatt) 跟史密特卡勒 (Schmidt-Kaler) 等人，在二〇〇三年展示了如何做到這點。這套技法廣泛使用在有用到超導迴路的研究工作上，薛可夫 (Schoelkopf) 跟紀爾文 (Girvin) 在二〇〇八年發表的論文中，將這套技法取名為「迴路QED」 (Circuit-QED) 。
小欄一：創造、移轉離子的重疊態。
想像有一個被困在阱裡的離子，最低電子態為 |↓> ，最低阱態為 |0> 。這個量子系統可以用下列式子表示：
|φ0> = |↓>|0>.
這個離子可用雷射脈衝加以激化，從而創造出一個同調重疊態：
|φ0>→|φ1> = (α|↓> + β|↑>) |0>.
「紅側帶」π-puls （頻率等於ω0 – ων ，見圖三）與離子產生交互作用。由於離子處在最低振動模式，只有 |↑>|0> 狀態會受到影響。離子躍遷到 |↓>|1> ，因此
|φ1>→|φ2> = α|↓> |0> + β|↓>|1> = |↓> (α|0>+β|1>).
重疊態就這樣移轉到離子的振動模式。倘若阱中還含有另一個離子，該離子會跟第一個離子具有相同的振動模式。如此一來重疊態就能夠以同樣的方式，移轉到第二個離子的內部態。
圖四：利用圓形雷德堡原子研究微波場態的實驗設置（見內文）。
空腔內的場可用在圓形雷德堡態（比方說 n = 50, l = |m|=49 ）的銣 (Rb) 原子加以探測。有些原子的範圍很大，半徑長達 125 奈米，與空腔內的場耦合性非常強。從n = 50 (|↓>) 躍遷到 n = 51 (|↑>) ，其頻率幾乎跟空腔內的微波場相同 (51 GHz) 。 R1 跟 R2 兩個空腔是用來創造介於 |↓> 跟 |↑> 之間受控制的量子重疊，並且加以分析。有個選擇性的場離子化偵測器 (D) ，是用來偵測原子狀態的。由同調來源製造出來的光子，透過波導管與空腔耦合。原子一次一個，以控制下的速度送進空腔裡，因此產生交互作用的時間也能受到控制。在哈羅契的研究團隊所進行的大多數實驗中，原子跟場的頻率有些微差異。在空腔內行進的原子並不會吸收光子，其能階反而會因為動態史塔克效應 (Stark effect) 而產生位移，微波場的相位變異也包括在內。這個相位位移的符號相反，要看這個原子是在 |↓> 還是 |↑> 的狀態而定，導致原子態與場態纏結（詳見布魯恩等人在一九九六年發表的論文）。
哈羅契等人在一九九〇年，提出一個以非破壞性量子測量法，測量空腔內光子數量的方法（詳見布魯恩等人同年發表的論文）。葛利澤斯 (Gleyzes) 等人在二〇〇七年用實驗展示實作方法，相關實驗亦可參考諾格斯 (Nogues) 等人在一九九九年的研究成果。他們在空腔中捕捉到個別的光子，並且透過它們與原子的互動加以觀察。關於這種測量方式的原理，在小欄二裡有更詳細的解說。由於有這種測量法，就產生了波函數的「漸進崩解」 (progressive collapse) ，可透過非破壞性量子測量法加以觀察的實驗。在這些實驗中，光子的數量在量測過程中即使有所增減，也可追蹤無誤（詳見古爾林 (Guerlin) 等人在二〇〇七年發表的論文）。
小欄二：如何測量空腔內的光子而不使其摧毀。
一個在 |↑> 狀態的原子在 B 的位子準備就緒（見圖四）。在 R1 有一股π/2 的脈衝，創造出 |↓> 跟 |↑> 原子態的重疊態，因此 |φ1> = (|↓> + |↑>)/√2.
重疊態在行經空腔 C 之後，就會變成 |φ> = (|↓> + eiφ |↑>)/√2 ，φ是原子態的重疊態在行經過程中累積的相位。由原子態的重疊態創造出來的原子雙極，其作用就像個時鐘一樣，而行經空腔過後的相位，就代表時鐘的指針位置。空腔內的微波場頻率與原子頻率略有出入。橫越空腔的原子並不會吸收或釋放光子，然而其能階卻會隨著產生位移，結果是相位 φ 會按照空腔內的光子數目而有所改變。
原子的行經時間是可以選定的，所以倘若空腔內沒有光子的話，φ = 0 mod 2π 。當原子抵達 R2 時，原子已位於重疊態 |φ1> 。原子在 R2 與另一道 π/2 的脈衝產生交互作用，因此 |φ1>→ |↓> ，這個現象由 D 偵測到。原子頻率與空腔內微波場頻率的出入也是可以選定的，因此倘若空腔內有一個光子的話，φ = π 。當原子在跟一個光子產生互動，抵達 R2 之後，原子已位於重疊態 |φ2> = (|↓>– |↑>) /√2 。原子跟 π/2 脈衝產生互動時， |φ2>→|↑> 。因此無論空腔內有 0 個還是 1 個光子，我們都有可能以非破壞性的方式加以測量。這種測量方式可以延伸到有幾個光子的情況，只要利用不同的相位跟幾個原子，重複類似的測量方式即可。
以實驗探討「薛丁格的貓」
圖五：薛丁格的貓。
哈羅契跟懷蘭德等人所領導的研究團隊，對於單一量子系統做到的控制程度，使他們得以在實驗室裡，利用光子跟離子進行類似薛丁格的貓的實驗（詳見哈羅契在一九九八年寫的文獻回顧）。大衛多維奇 (Davidovich) 等人在一九九六年提出一個實驗設計，哈羅契的研究團隊隨即著手實作，把一個雷德堡原子跟空腔場纏結，藉此創造出一個類似薛丁格的貓的微波場態重疊。這樣的重疊非常脆弱，只要跟環境耦合便會輕易被摧毀（在這個例子中，指的是逃離空腔的光子）。這個重疊的脫散現象（也就是演變為一個統計上的混態）可以當成一個時間與重疊態特性函數來加以測量。懷蘭德等人利用離子阱技法，進行了類似的實驗，他們創造出跟運動同調態纏結的受困單一離子，用這些離子來構成「貓態」（詳見門羅等人在一九九六年發表的論文），並觀察其脫散現象（詳見彌亞特 (Myatt) 等人在二〇〇八年所做研究）。哈羅契等人最近創造出貓態，加以測量並且拍了一部影片，展示貓態如何從重疊態演變成古典混態（詳見戴樂葛利瑟 (Deléglise) 等人在二〇〇八年發表的論文）。這種超凡的控制程度，也使得他們得以做出量子回饋機制，對脫散效應進行測量並加以修正，從而「穩定」量子態，比方說使其穩定在一個給定的福克態（詳見賽林 (Sayrin) 等人在二〇一一年的研究成果）。
量子電腦
席哈克跟左勒在一九九五年發表了一篇極具影響力的理論性文章，指出可用被困住的離子建造一台量子電腦。我們可將量子位元 (qubits) 編碼到被困離子的超精細能階中，因為被困離子與環境的互動非常弱，因此保存時間就可拉長。藉由質心運動，兩個以上的離子都能夠加以耦合（如小欄一所示）。懷蘭德的研究團隊率先進行鈹離子 (Be+) 運動與旋轉的二量子位元（受控否閘 (CNOT) ）實驗（詳見門羅等人於一九九五年發表的論文），從那之後，以被困離子為基礎的量子資訊研究領域，就有了相當可觀的進展。奧地利因斯布魯克大學的布拉特等人，在二〇〇三年做到了用鈣離子 (Ca+) 進行 CNOT 運算（詳見史密特卡勒等人在當年的研究成果）。時至今日，最先進的量子電腦科技是根據被困離子做出來的，並且可運用多達 14 個量子位元，以及一系列的運算閘與運算協定（詳見布拉特與懷蘭德在二〇〇八年所寫的文獻回顧）。不過未來若要研發出運算能力能夠超越古典電腦之所及的大型裝置，則需要克服相當多的挑戰。
光學鐘
光學鐘是懷蘭德研究被困離子的一項重要應用。根據在可見光區域的離子躍遷做出來的光學鐘之所以有意思，是因為可見光或紫外線光的躍遷頻率，比起在無線電波範圍運作的銫原子鐘躍遷頻率，嘖嘖高出了好幾個數量級。懷蘭德等人研發出來的光學鐘（如迪達姆斯 (Diddams) 等人在二〇〇一年，羅森班德 (Rosenband) 等人在二〇〇八年，以及周清文等人在二〇一〇年所做的），目前的精確度剛好可達到10-17 以下，比目前銫原子鐘的頻率標準還要精確兩個數量級。
光學離子鐘靠的是對攝動不怎麼敏感的單一離子狹窄躍遷（又稱禁戒躍遷 (forbidden transition) ）。這離子也必須要具有強烈的容許躍遷 (allowed transition) ，才能夠有效地加以冷卻，供人偵測。懷蘭德等人研發出一種叫做「量子邏輯光譜分析」 (quantum logic spectroscopy) 的新技法，靠的是兩種離子的纏結狀態，如小欄一所示。使用這個技法時，其中一個離子提供光譜躍遷（比方說 1S0→3P1 在 27Al+ (267 奈米) ），另一個離子（比方說 9Be+）則有強烈的冷卻躍遷（詳見史密特 (Schmidt) 等人在二〇〇五年發表的論文）。兩個不同光學鐘的精確度，可以透過由洪許跟霍爾 (Hall) 發明的頻梳 (frequency comb) 技法進行比較，他們兩位藉此獲頒二〇〇五年諾貝爾物理獎。
最近光學鐘所達到的精確度，使懷蘭德等人得以測量相對論效應，比方說在時速幾千公里下的時間擴大現象，或是兩點間僅有大約 30 公分高度差時的重力勢能差（詳見周清文在二〇一〇年發表的論文）。
總結
懷蘭德與哈羅契發明了可以用高精確度，對個別量子系統進行測量與控制的新科技，並且實作成功。他們的研究成果使我們得以透過測量類似「薛丁格的貓」狀態的演變過程，來研究脫散現象，這對於開發量子電腦，研發極為精確的光學鐘，邁出了第一步。
–
研究出處：2012諾貝爾物理獎原文介紹
責任編輯：Nita Hsu
No comments yet.
【我的自己人】
2013台積電盃青年尬科學 本活動結合「聽」、「說」、「讀」、「寫」的面相，使科普傳播寓教於樂的學習。
CASE 科學教育發展中心首頁 國立台灣大學科學教育發展中心首頁
科學人文跨科際計畫
跨科際科學營
鏈結
12年國教論壇 作為一個開放的網路平台，希望能廣納各方不同面向的意見，針對台灣教育問題做全面性的深入探討。
CASEdu教育平台 CASEdu是由臺大科學教育發展中心所成立的教育平台。處於國家教育政策的變動時期，我們期許能匯集建設性的專業意見，歡迎對教育有熱忱的朋友一同參與討論。
國科會高瞻計畫資源平台 高瞻是國科會為提升高中職學生科技教育品質、改善科技教材而進行的一項計畫，在高瞻的資源平台內有各科種子教師的心血結晶，非常適合中學老師閱讀！
No comments:
Post a Comment