 蘋果和地球之間的萬有引力,可以將地球的萬有引力視為質量集中在地心處嗎?
蘋果和地球之間的萬有引力,可以將地球的萬有引力視為質量集中在地心處嗎?
 蘋果和地球之間的萬有引力,可以將地球的萬有引力視為質量集中在地心處嗎?
蘋果和地球之間的萬有引力,可以將地球的萬有引力視為質量集中在地心處嗎?剥皮法则_百度百科
baike.baidu.com/view/5532293.htm
轉為繁體網頁
球体(密度呈球对称分布)内部空间的拓展——对球内任一距球心为r的一质点A的吸引力等效于质量与半径为r的球的质量相等且位于球心的质点对质点A的吸引。...
baike.baidu.com/view/5532293.htm
轉為繁體網頁
球体(密度呈球对称分布)内部空间的拓展——对球内任一距球心为r的一质点A的吸引力等效于质量与半径为r的球的质量相等且位于球心的质点对质点A的吸引。...轉為繁體網頁
有一质量为M,半径为R的密度均匀球体,在距离球心O为2R的 ...
gaokao.hujiang.com/tiku/p1202392/
轉為繁體網頁
有一质量为M,半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的 ... 但当球体被挖去一部分后,由于质量分布不均匀,万有引力定律就不再适用.
gaokao.hujiang.com/tiku/p1202392/
轉為繁體網頁
有一质量为M,半径为R的密度均匀球体,在距离球心O为2R的地方有一质量为m的 ... 但当球体被挖去一部分后,由于质量分布不均匀,万有引力定律就不再适用.轉為繁體網頁
[DOC]下载浏览该文件2008824193755189 - 浙江省湖州中学
www.hzhs.net/uploadfile/2008824193755189.doc
轉為繁體網頁
若质点质量为m,与球心的距离为R。设球的半径为a,密度为,质量为。 ... 如果场点P
www.hzhs.net/uploadfile/2008824193755189.doc
轉為繁體網頁
若质点质量为m,与球心的距离为R。设球的半径为a,密度为,质量为。 ... 如果场点P轉為繁體網頁
[DOC]重力場積分
memo.cgu.edu.tw/yun-ju/CGUWeb/.../H105GravitationIntegral.doc
設質量M、半徑R之半圓環的線密度為λ(單位:kg/m),求圓心位置處之重力場強度。 ... 就是:「質量均勻分佈的球對外部質點的吸引力,看起來像所有質量都集中在球心 ...
memo.cgu.edu.tw/yun-ju/CGUWeb/.../H105GravitationIntegral.doc
設質量M、半徑R之半圓環的線密度為λ(單位:kg/m),求圓心位置處之重力場強度。 ... 就是:「質量均勻分佈的球對外部質點的吸引力,看起來像所有質量都集中在球心 ...李晓鹏:年轻人,你活着不是为了观察K线做布朗运动
这篇文章本来是该几年前写的,奉劝大家不要去玩股票。因为那个时候我的《中国崛起的经济学分析》这本书刚刚出版,里面用“破坏性要素参与分配”的理论来分析了中国经济。在写作过程中我发现这个理论也可以顺便用来解释股票市场,让大家看清楚股票市场的本质。但当时的大盘指数才1980点,我怕写出来很多人会被我“忽悠”,把手里的股票“割肉”卖掉,回头会恨死我。所以就忍了。
我的观点很简单:股票市场不是年轻人应该去的地方。对年轻人来说,玩股票就跟爱上赌博一样,是在浪费生命。年轻人最大的资本是自己,一旦把自己有限的积蓄投入到股市中去,就会被行情的波动死死的抓住,然后在里面虚度光阴:原本应该学英语的时间,却拿来研究波[……]
我的观点很简单:股票市场不是年轻人应该去的地方。对年轻人来说,玩股票就跟爱上赌博一样,是在浪费生命。年轻人最大的资本是自己,一旦把自己有限的积蓄投入到股市中去,就会被行情的波动死死的抓住,然后在里面虚度光阴:原本应该学英语的时间,却拿来研究波[……]
统计物理学中的“最小作用量原理” - 心情随笔网
www.huangi.com/article/75283596824/
轉為繁體網頁
经典力学中力学系统的运动规律的最一般表述由“最小作用量原理”给出。我觉得,“轉為繁體網頁
关于最小作用量原理2_百度文库
wenku.baidu.com/view/b3c737fd700abb68a982fbc2.html - 轉為繁體網頁
2010年12月12日 - 物理学关于最小作用量原理刘大为(甘肃联合大学理工学院, ... 作用量函数L=一mc作用量,熵(体系,理想氣體)狀態函數,路徑無關;最小作用量原理 ...
blog.sina.com.cn/s/blog_a582cd40010178x9.html
轉為繁體網頁
2012年7月18日 - 作用量狀態函數 的結果(無引號): ... 薛定谔是一个聪明人,他知道这个世界上,孤立体系熵是增加的(也就是说,孤立 ... 其中s是作用量,ψ是波函数。轉為繁體網頁
熵- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/熵
熵亦被用於計算一個系統中的失序現象,也就是計算該系統混亂的程度。熵是一个描述系统状态的函数,但是经常用熵的参考值和变化量进行分析比较,它在控制论、关于最小作用量原理_CNKI学问
xuewen.cnki.net/CJFD-KXJS200710032.html - 轉為繁體網頁
关于最小作用量原理-1对于三种基本原理目前被认知的普遍程度的评述任何自然事物的变化 ... 沿用普通分析力学中的研究思路,引入两个新广义动量和新Hamil-ton标度,对数,熵,概率,信息,最小作用量- ideaflying的日志 ...
ideaflying.blog.163.com/.../23536005220149610105188...
轉為繁體網頁
2014年10月6日 - Nottale的标度相对论主要分成两大块,一块是纯粹的相对论,他仿照爱因 ... 信息熵轉為繁體網頁
稳定作用量原理_搜索_互动百科
www.baike.com/wiki/稳定作用量原理 - 轉為繁體網頁
稳定作用量原理,互动百科搜索. ... 周向作用量_百科词条. 是指,当波流同向时,波变平缓;当波流反向时,波明显变陡.随着波流强度的增加,非线性的 ... 作用量作额外的限制。我们假设S[φ]是M上的如下函数的积分称为拉格朗日量,它. ... 熵量守恒定律 ...万门大学|新闻|[万门大学杯]第一届理论物理知识竞赛
www.wanmen.org/blogs/36
轉為繁體網頁
系统的拉氏量L可以减去“任意函数f对时间的全导数”而不改变其物理演化。 2. 场论中的作用量密度L是t,x,y,z的函数,经典力学中的作用量是t的函数. 3. 四维磁矢势A ...轉為繁體網頁
swordi:【原创】地球瓶颈中的达尔文主义 (一) 2015-01-09 08:13:47
 忽然想明白你这个“觅母”是MEME的意思 [ 原手 ] 于:2015-01-09 08:13:47 复:4085144
忽然想明白你这个“觅母”是MEME的意思 [ 原手 ] 于:2015-01-09 08:13:47 复:4085144
为什么不翻译成咪咪呢,不过发音是咪一。
还以为与母系社会有什么关系呢,猜了半天。
裴多菲的这首诗通过你的诠释,变成这样:
肉体诚可贵
进化价更高
若为觅母故
二者皆可抛
一听之下,裴多菲有恋母症。
你最后提出一个有意思的问题,永生啦,伟大啦不说,人生原本不过是基因的傀儡,不但生老病死身不由己,就是喜怒哀乐,勾心斗角,基本上也是不由自主的。
时下一个时髦的话题是人到底有多少自由意志(free will),这个是牵涉了心理学,哲学,生物学,脑神经,物理,化学,计算机等广泛领域内的大讨论。
裴多菲让人怀念之处在于他提出了人战胜基因操控的一种尝试,或者说就是觅母破土而出之前的呐喊。
生命或者肉体,或者我们常说的“人”仍然不过是在基因或者觅母的控制下的化学品。虽然可以叫做人的生物性,社会性,不过这很可能是肉体们的一厢情愿,只是基因让你这样想的(还相信自由意志么?)。
觅母有着自己的未来,这也是觅母与基因在裴多菲这具肉体上争斗的本质,觅母要脱离肉体,而基因不让觅母脱离肉体,当然在裴多菲的例子中,觅母赢了,我们现在人人都会背诵他的这个诗。但在绝大多数的例子中,基因是稳操胜券的,英雄难过通奸关,五斗米折腰随处可见。
还以为与母系社会有什么关系呢,猜了半天。
裴多菲的这首诗通过你的诠释,变成这样:
肉体诚可贵
进化价更高
若为觅母故
二者皆可抛
一听之下,裴多菲有恋母症。
你最后提出一个有意思的问题,永生啦,伟大啦不说,人生原本不过是基因的傀儡,不但生老病死身不由己,就是喜怒哀乐,勾心斗角,基本上也是不由自主的。
时下一个时髦的话题是人到底有多少自由意志(free will),这个是牵涉了心理学,哲学,生物学,脑神经,物理,化学,计算机等广泛领域内的大讨论。
裴多菲让人怀念之处在于他提出了人战胜基因操控的一种尝试,或者说就是觅母破土而出之前的呐喊。
生命或者肉体,或者我们常说的“人”仍然不过是在基因或者觅母的控制下的化学品。虽然可以叫做人的生物性,社会性,不过这很可能是肉体们的一厢情愿,只是基因让你这样想的(还相信自由意志么?)。
觅母有着自己的未来,这也是觅母与基因在裴多菲这具肉体上争斗的本质,觅母要脱离肉体,而基因不让觅母脱离肉体,当然在裴多菲的例子中,觅母赢了,我们现在人人都会背诵他的这个诗。但在绝大多数的例子中,基因是稳操胜券的,英雄难过通奸关,五斗米折腰随处可见。
千里积于跬步——流,向量场,和微分方程
在很多不同的科学领域里面,对于运动或者变化的描述和建模,都具有非常根本性的地位——我个人认为,在计算机视觉里面,这也是非常重要的。
 这个S(t, x)呢,可以从两个方面去看,就得到两种不同的理解。首先,固定 t,
这个S(t, x)呢,可以从两个方面去看,就得到两种不同的理解。首先,固定 t,
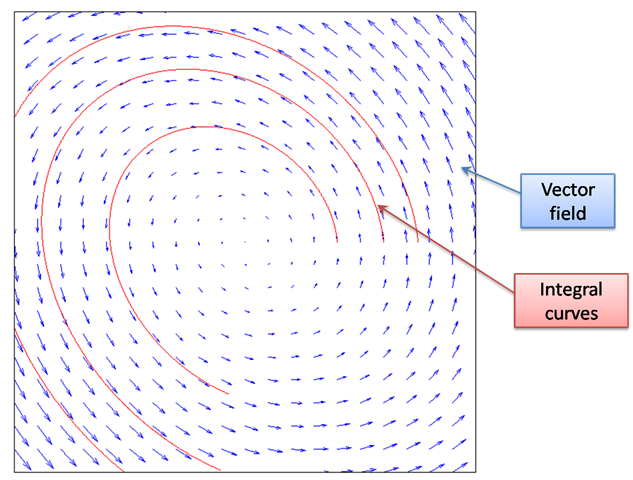 我不打算给出严格的证明,这可以在很多微分流形的相关资料中找到。这里,我希望用一个通俗的过程来介绍,怎么构造出这个流。我们把向量场看成是在一个大地图上标了很多很密的指示牌——告诉你到了这点后应该用多大的速度往什么方向开车。于是,你从某个地方出发,你先看看附近的指示牌,把车子调整到指示的速度和方向,往前开一小段后看到下一个指示,继续调整速度和方向,一直这样下去,你开车的过程就形成了一个运动轨迹,而且在各点上的速度,都和该点的指示一致。设想一个极限过程,指示牌无限密集,开车的人每个时刻都在连续地调节速度,那么就得到了一个和向量场一致的运动曲线。我们上面说过,流是所有这些运动曲线的集体,于是我们从不同的地方开始开车,最后就能把整个流构造出来了。 有些时候,向量场的定义域可能不是很完整,那么车子不能无限开下去(不然可能开出去了),这时候只能给出“局部的流”。如果一个向量场存在一个全局的流,就叫做完备的向量场(Complete Vector Field)。 从这个故事,我们知道一个变换是怎么炼成的:就是按照指示,一步步的做,这些小步积累起来,就形成最后的变换效果。有什么样的指示,就会有什么样的变换。在李群论中,数学家给向量场起了个名字:infinitestimal generator——寓意是,千里变换,生于跬步。数学上,“千里”与“跬步”的关系,就是李群和李代数的联系。 为什么我们不直接描述变换,而言描述生成它的向量场呢?很简单,很多时候全局的演化不容易直接描述,而小步的前进则是很容易把握的。在很多问题中,我们知道“divide and conquer“的策略能够大大简化问题,从变换群到向量场正是这种策略的极限体现。一个简单的例子,比如我们要表示一个不会改变物体大小的变换过程,所谓“不可压缩性”如果用变换矩阵直接表达,那是一个颇为复杂的非线性约束,而如果使用向量场表达,我们只需要把向量场限制在某个有限维子空间里——这就是一个简单得多的线性约束。这样的例子还有很多很多。
我不打算给出严格的证明,这可以在很多微分流形的相关资料中找到。这里,我希望用一个通俗的过程来介绍,怎么构造出这个流。我们把向量场看成是在一个大地图上标了很多很密的指示牌——告诉你到了这点后应该用多大的速度往什么方向开车。于是,你从某个地方出发,你先看看附近的指示牌,把车子调整到指示的速度和方向,往前开一小段后看到下一个指示,继续调整速度和方向,一直这样下去,你开车的过程就形成了一个运动轨迹,而且在各点上的速度,都和该点的指示一致。设想一个极限过程,指示牌无限密集,开车的人每个时刻都在连续地调节速度,那么就得到了一个和向量场一致的运动曲线。我们上面说过,流是所有这些运动曲线的集体,于是我们从不同的地方开始开车,最后就能把整个流构造出来了。 有些时候,向量场的定义域可能不是很完整,那么车子不能无限开下去(不然可能开出去了),这时候只能给出“局部的流”。如果一个向量场存在一个全局的流,就叫做完备的向量场(Complete Vector Field)。 从这个故事,我们知道一个变换是怎么炼成的:就是按照指示,一步步的做,这些小步积累起来,就形成最后的变换效果。有什么样的指示,就会有什么样的变换。在李群论中,数学家给向量场起了个名字:infinitestimal generator——寓意是,千里变换,生于跬步。数学上,“千里”与“跬步”的关系,就是李群和李代数的联系。 为什么我们不直接描述变换,而言描述生成它的向量场呢?很简单,很多时候全局的演化不容易直接描述,而小步的前进则是很容易把握的。在很多问题中,我们知道“divide and conquer“的策略能够大大简化问题,从变换群到向量场正是这种策略的极限体现。一个简单的例子,比如我们要表示一个不会改变物体大小的变换过程,所谓“不可压缩性”如果用变换矩阵直接表达,那是一个颇为复杂的非线性约束,而如果使用向量场表达,我们只需要把向量场限制在某个有限维子空间里——这就是一个简单得多的线性约束。这样的例子还有很多很多。
什么是“流”?
在我接触过的各种数学体系中,对于运动和变化的描述,我感觉最为适合的有两种不同的perspective:流和变换群。前者以被作用的对象为中心,运动就是这个东西随时间变化的函数;后者以变换本身为中心,研究的是各种变换所组成的空间的代数和拓扑结构。我想,相对来说,前者对于多数人而言似乎更为直观。在这篇文章里,就以“流”(Flow)的角度展开了。其实,这两种思路有着根本的联系——这种联系体现在李群论的一个基础概念——李群作用(Lie Group Action),以及由它所延伸出来的丰富的理论。 流(Flow)是什么呢?很通俗的说,表示了一种运动规则。给定一个点的初始位置 x,让它运动一段时间 t,那么之后到达另一个位置 y,那么 y 就是初始位置 x 和运动时间 t 的函数:y = S( t, x )这个函数 S,如果符合一些合理的性质,就叫做一个流(Flow)。学过微分几何的同学可能会觉得这个定义与数学中的严格定义有点差距——确实如此。在微分几何中,流的概念需要建立在流形和单参数子群或者积分曲线的基础上,在一篇Blog文章中很难按照这样的方式阐述。只好在一定程度上放弃严密性,从直观出发,希望能传递出最基本的思想。 我们想想, 一个合理的运动函数应该具有什么性质呢?我想,最起码应该有三点:
- 运动是连续的。物理学告诉我们,现实中没有所谓的“瞬间转移”。在上面的式子中,如果固定 x,那么 y( t ) = S(t, x) 就是这个初始位置在 x 的点的运动过程。在数学上,没有“瞬间转移”就是说对于任何 x,它的运动过程 y( t ) 都是连续的。
- 变形是连续的。现在假设我们不考虑一个点,而是考虑一个物体。那么,本来是邻居的点,后来还是邻居——严格一点,在拓扑学上就是说,x 和它的一个邻域各自都运动了时间 t,那么运动后,这个邻域关系还是保持的——这等价于不改变这个物体的拓扑结构(比如,不把它撕开,但是连续变形是肯定允许的)。当然,在现实中物体被撕开不是没有可能,但是这会导致拓扑结构的改变,这就不是一般的数学工具所用表达的了。
- 时间上的一致性。简单的说,如果我先让它运动时间 t1,在运动时间 t2,那么和让它运动时间 (t1 + t2)是一样的。用上面这个表达式写,就是:S( t2, S( t1, x) ) = S(t2 + t1, x)。这个性质在物理上似乎理所当然,但是在数学上,你随便给一个二元函数S,可就未必符合这个属性了。这个规定保证了,我们定义出来的 S 最起码在物理上不会出现错乱。但是,它的意义不止于此,后面我们会看到,它在代数上,表示了一个群同构映射(Group homomorphism)——这种映射在李代数中有着核心作用。
流——变换群和运动曲线的统一
 这个S(t, x)呢,可以从两个方面去看,就得到两种不同的理解。首先,固定 t,
这个S(t, x)呢,可以从两个方面去看,就得到两种不同的理解。首先,固定 t,T_t ( x ) = S(t, x)它就变成了一个关于x的变换函数:把一个点从一个位置变换到时间 t 后的另外一个位置。那么 T_t 就是一个变换。然后,不同的时间 t,对应着一个不同的变换。而且基于时间的一致性,先做 T_(t1) 变换 (走时间 t1),再做 T_(t2) 变换(再走时间 t2),相当于另一个变换 T_(t2 + t1)。数学上就是:T_(t2) * T_(t1) = T_(t2 + t1)。如果你对群的概念有基本的了解,这里就可以看出来,从全部的不同时间的T_t 构成了一个变换群,从 t 到 T_t 的映射,就是从实数R上的加法群到这个变换群的同构映射。因为 T_t 是由一个参数 t 控制的,有个专门的名词,叫做“单参数群”(one-parameter group)。由于加法群的可交换性,这个单参数变换群也是可交换的——这个可交换性的物理意义很明显: 先走t1,再走t2;还是先走t2,再走t1,是一样的。 因此,我们得到了第一种理解:流,就是连续作用在一个物体上的可交换单参数变换群。(这里所谓“物体”,在数学上有专门的名字“流形”,对于这点我不想展开太多了。)其实,这才是关于流的比较正规的定义。 从另外一个角度上看,固定 x,我们追踪这一个点的运动, y_x ( t ) = S(t, x) 那么 y_x 就是初始位置(t=0时的位置)为 x 的点的运动过程——也叫做运动曲线(curve) 或者运动轨迹(orbit)。每个点都有自己的运动曲线,所谓流,就是这所有的这些运动曲线的共同体,或者说,流就是由这些运动曲线刻画的——这和我们一些直观的想法是一样的——我们在画画时喜欢在河上画几条曲线来表示流动。 这个函数S(t, x),把变换群和运动曲线同一起来了——它们就是一个东西的两个不同侧面。到这里,我们向我们的目标迈出了第一步——最终,我们是要把变换群和向量场联系在一起——这就是李群和李代数的核心所在。
流与向量场
继续我们的故事。现在,我们有了y_x( t ),那么对它求导,我们就可以得到这个点在各个时刻的速度。整个流行就是所有这些曲线的集合,这样,在流形上的每个点,我们都能找到经过它的一条曲线,从而标出这点的速度。(这里强调一点,对于一个给定的流,经过某点的曲线是唯一的,你可以想想为什么?)于是,我们给每个点都赋予了一个速度,这就是“速度场”(velocity field)。每个速度就是曲线上的一个切向量,所以更一般的说,我们把它叫做“向量场”。这里,我们看到,任意一个流都可以通过运动曲线的速度来建立一个对应的向量场。而且可以证明,这个向量场是连续的。 那么反过来呢?我们给定一个连续的向量场,能不能找到一个流和它对应呢?这里面有三个方面- (存在性),能不能找到一个流,它的速度场等于给定的向量场。
- (唯一性),如果存在,这个流是不是唯一的。
- (连续性),这个流 S(t, x) 是不是关于 x 和 t 的连续函数(或者光滑函数)。
 我不打算给出严格的证明,这可以在很多微分流形的相关资料中找到。这里,我希望用一个通俗的过程来介绍,怎么构造出这个流。我们把向量场看成是在一个大地图上标了很多很密的指示牌——告诉你到了这点后应该用多大的速度往什么方向开车。于是,你从某个地方出发,你先看看附近的指示牌,把车子调整到指示的速度和方向,往前开一小段后看到下一个指示,继续调整速度和方向,一直这样下去,你开车的过程就形成了一个运动轨迹,而且在各点上的速度,都和该点的指示一致。设想一个极限过程,指示牌无限密集,开车的人每个时刻都在连续地调节速度,那么就得到了一个和向量场一致的运动曲线。我们上面说过,流是所有这些运动曲线的集体,于是我们从不同的地方开始开车,最后就能把整个流构造出来了。 有些时候,向量场的定义域可能不是很完整,那么车子不能无限开下去(不然可能开出去了),这时候只能给出“局部的流”。如果一个向量场存在一个全局的流,就叫做完备的向量场(Complete Vector Field)。 从这个故事,我们知道一个变换是怎么炼成的:就是按照指示,一步步的做,这些小步积累起来,就形成最后的变换效果。有什么样的指示,就会有什么样的变换。在李群论中,数学家给向量场起了个名字:infinitestimal generator——寓意是,千里变换,生于跬步。数学上,“千里”与“跬步”的关系,就是李群和李代数的联系。 为什么我们不直接描述变换,而言描述生成它的向量场呢?很简单,很多时候全局的演化不容易直接描述,而小步的前进则是很容易把握的。在很多问题中,我们知道“divide and conquer“的策略能够大大简化问题,从变换群到向量场正是这种策略的极限体现。一个简单的例子,比如我们要表示一个不会改变物体大小的变换过程,所谓“不可压缩性”如果用变换矩阵直接表达,那是一个颇为复杂的非线性约束,而如果使用向量场表达,我们只需要把向量场限制在某个有限维子空间里——这就是一个简单得多的线性约束。这样的例子还有很多很多。
我不打算给出严格的证明,这可以在很多微分流形的相关资料中找到。这里,我希望用一个通俗的过程来介绍,怎么构造出这个流。我们把向量场看成是在一个大地图上标了很多很密的指示牌——告诉你到了这点后应该用多大的速度往什么方向开车。于是,你从某个地方出发,你先看看附近的指示牌,把车子调整到指示的速度和方向,往前开一小段后看到下一个指示,继续调整速度和方向,一直这样下去,你开车的过程就形成了一个运动轨迹,而且在各点上的速度,都和该点的指示一致。设想一个极限过程,指示牌无限密集,开车的人每个时刻都在连续地调节速度,那么就得到了一个和向量场一致的运动曲线。我们上面说过,流是所有这些运动曲线的集体,于是我们从不同的地方开始开车,最后就能把整个流构造出来了。 有些时候,向量场的定义域可能不是很完整,那么车子不能无限开下去(不然可能开出去了),这时候只能给出“局部的流”。如果一个向量场存在一个全局的流,就叫做完备的向量场(Complete Vector Field)。 从这个故事,我们知道一个变换是怎么炼成的:就是按照指示,一步步的做,这些小步积累起来,就形成最后的变换效果。有什么样的指示,就会有什么样的变换。在李群论中,数学家给向量场起了个名字:infinitestimal generator——寓意是,千里变换,生于跬步。数学上,“千里”与“跬步”的关系,就是李群和李代数的联系。 为什么我们不直接描述变换,而言描述生成它的向量场呢?很简单,很多时候全局的演化不容易直接描述,而小步的前进则是很容易把握的。在很多问题中,我们知道“divide and conquer“的策略能够大大简化问题,从变换群到向量场正是这种策略的极限体现。一个简单的例子,比如我们要表示一个不会改变物体大小的变换过程,所谓“不可压缩性”如果用变换矩阵直接表达,那是一个颇为复杂的非线性约束,而如果使用向量场表达,我们只需要把向量场限制在某个有限维子空间里——这就是一个简单得多的线性约束。这样的例子还有很多很多。 和微分方程的联系
最后,我们再回头看看上面这个“从向量场推导流”的问题。我们知道所谓速度场,就是对 t 的导数,所以这个问题,可以写成:给定向量场 V(x), 求 S(t, x) 使得 d S(t, x) / dt = V(x), 并且 S(0, x) = x这就是一般意义的常微分方程的初值问题。对这个问题的回答,和对于常微分方程的解得存在性,唯一性和连续性的回答,是联系在一起的。给定一个向量场,就相当于给出一个常微分方程。如果给定 x, 那么所形成的曲线 y_x ( t ),就是上述微分方程的解,而流 S(t, x) 就是所有这些解的整体。我们知道微分方程的解通常以积分形式给出,所以上面说的“运动曲线”,在数学上有个正式的学名叫“积分曲线”(Integral curve)。 在物理上,“积分曲线”也是很容易理解的,就是把“速度指示牌”的指示积累起来形成的路径,积分曲线生成的过程就是“积跬步而致千里”的过程。而且,这不仅仅是一种形象思考,在实际问题中微分方程的数值解法正好就是这种过程的最好体现。
剥皮法则编辑
本词条缺少名片图,补充相关内容使词条更完整,还能快速升级,赶紧来编辑吧!
球体(密度呈球对称分布)内部空间的拓展——对球内任一距球心为r的一质点A的吸引力等效于质量与半径为r的球的质量相等且位于球心的质点对质点A的吸引 。
中文名
类 别
法则
特 点
密度呈球对称分布
证 明
球壳证明
目录
1球体编辑
球体(密度呈球对称分布)内部空间的拓展——对球内任一距球心为r的一质点A的吸引力等效于质量与半径为r的球的质量相等且位于球心的质点对质点A的吸引 。
2球壳编辑
球壳(密度呈球对称分布)内部空间的拓展 ——对球壳内任一位置上任一质点A的吸引力都为零。
3证明编辑
球壳证明(球体可视为去掉球壳)
证明:设球壳内任一位置上任一质点A质量为m,对球内任一距球心为半径的一质点的质量为M,取过A点的两条弦(十分靠近)EC,BD.
令∠DAE=∠BAC=α→0,
则EA=DA,BA=CA
F(D对A)=(GMm)/AD² ①
由于上述夹角非常小,所以DE,BC之间的曲面可以视为一个圆(我只是淮南一中高一学生,不会求一部分球面对面积,所以只有近似,欢迎高手来修改为更好的解法)
S(DE之间)=π[1/2(ADα)]² ③
S(BC之间)=π[1/2(ACα)]² ④
F(ED之间的圆曲面对A)=①×③
F(BC之间的圆曲面对A)=②×④
上述两式大小相等方向相反,合力为O
整个球壳以此类推
得,球壳对球壳内任一位置上任一质点A的吸引力都为零。
以上证明均为淮南一中2013届学生证明,由于知识有限,如有不妥敬请见谅。
据说高等教育出版社出版的《力学》有相关严谨的证明,有需要有条件者可购买查阅
這是 http://phy.ntnu.edu.tw/~yao/newton-central-force.pdf 的 HTML 檔。
G o o g l e 在網路漫遊時會自動將檔案轉換成 HTML 網頁。
G o o g l e 在網路漫遊時會自動將檔案轉換成 HTML 網頁。
| Page 1 |


No comments:
Post a Comment