"选定一个力学量
 表象时,就相当于选定这个希尔伯特空间的一个坐标系"
表象时,就相当于选定这个希尔伯特空间的一个坐标系""设有Descartes坐标架转动 这里 。其中 为三个Euler角, 为矢 量表示的三个角。于是有 现执行一个向二维空间的投影,即以投影算符P 作用,得三 个POVM如下"
【精品文档】量子理论基础中的疑难问题及open问题
http://www.docin.com/p-117820922.html
Feynman 发明了路径积分以后,量子理论看起来便不那么反传统了,路径积分的被积函数都是经典的,交换的力学量,被一个幺模复值泛函加权,得到经典观测值"
倒三角是一个算符,意思是分别对ψ(x,y,z)的x,y,z坐标求偏导的平方和, ▽2ψ(x,y,z)+(8π2m/h2)[E-U(x,y,z)]ψ(x,y,z)=0
"矩阵力学和波动力学统一在“变换理论”框架下,这使得具有深刻分析背景的 von Neumann 意识到,某种函数空间上的微分算子理论对应于波动力学,而这种空间的代数结构可以用来归纳矩阵力学。因为这种函数空间已经被 Hilbert 的学生 Schmidt 研究过,而大家普遍相信是 Hilbert 的思想引导了对这种函数空间的研究,所以 von Neumann 用了 Hilbert space 这个名字。 据数学史研究者澄清,Hilbert space 的主要思想基本来自于 Schmidt 本人。von Neumann 的名著〈量子力学的数学基础〉用分析和代数的结合体 --- 算子代数来描述量子物理,他的基本定理是 Stone-von Neumann 定理:由坐标和动量生成的“Heisenberg 代数” [tex][Q,P]=\mathrm{i}\hbar[/tex] 只有唯一的自伴表示等价类,其中一个代表的表示空间是坐标的平方可积函数空间,坐标和动量分别表示为算子
这种对量子理论的理解可以大致总结为“非交换”观点,因为 Hilbert 空间
http://quantway.lofter.com/post/42866f_179de26
如果我们利用某个关系函数,比如Y=F(X),代入一个X算出一个Y,又将Y作为新的X再次计算下一个Y………如此不断,这种方法在数学上称为迭代,
Clifford 几何代数的基本观点
||
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
"随机函数的谱分解 Feynman 发明了路径积分以后,量子理论看起来便不那么反传统了,路径积分的被积函数都是经典的,交换的力学量,被一个幺模复值泛函 加权,得到经典观测值
DF]取值于von Neumann代数的测度
将Kluvanek延拓定理推广到一弱可列可加测度,并证明了域上的正规正算子测度. 在该域所张成的。一域上有惟一的弱可列可加延拓. 关键词:算子测度; 弱可列可加 ...
运算量子物理学_百度百科
书中利用量子理论的概率结构,用运算量子物理学给出量子力学一个系统表述。书中把可观测量视为正算子测度,并深入探索而得到量子测量理论,从而应用它...
[PDF]σ- 弱算子拓扑下的测度与积分Ξ
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
2View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
1View count
6/28/15
0Comment count
2View count
6/28/15
0Comment count
1View count
6/28/15
http://media.open.com.cn/media_file/rm/dongshi2005/liangzilixue/E_index5.htm
选定一个力学量
 表象时,就相当于选定这个希尔伯特空间的一个坐标系
表象时,就相当于选定这个希尔伯特空间的一个坐标系"POVM举例——单qubit两维态空间中的POVM 选择N个3维单位矢量 和N个正实数 ,使它们满足: 由此便可构造一组N个元素的POVM: 这里 是态的极化矢量。 自旋态的投影算符和 关系为 共计N个,都是非负的、厄密的,并且 。 这N个 就在此qubit二维态空间中定义了一个POVM。 注意,在两维态空间中作单位算符POVM分解时,若是两个分 解,分解虽有无穷多种,但必定都是正交的: 只有多于所在空间维数的分解,即 的分解,才必定是非正 交分解。比如N=3,若取任意三角形的三个边作为(首尾相接 的)三个矢量 ,有 ,再选比如 ,便 得到一组三个如下POVM, 。由乘积知, 它们已不再是正交投影,各自迹也不是1。 α α α F = λ 1+n σ 1 2 α α λ = 1 n 0 n α α α α 1 E = n n = 1+ n σ 2 I n I F α α α F = 2λ E F 2 1 F F n n n n I ) 3 , 2 , 1 ( n 0 3 2 1 n n n 3 1 3 2 1 3 , 2 , 1 ; 3 2 1 3 1 n E n F 3 N n α α F E α 0 < λ < 1 24 另一个在三维执行正交投影在两维观察的POVM例子。 设有Descartes坐标架转动 这里 。其中 为三个Euler角, 为矢 量表示的三个角。于是有 现执行一个向二维空间的投影,即以投影算符P 作用,得三 个POVM如下"
§5。3 狄拉克符号
 。 (5.3.1)
。 (5.3.1)
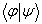 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 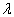 为任一复数,由上式得到
为任一复数,由上式得到
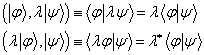 。 (5.3.2)
。 (5.3.2)
 , 当且仅当
, 当且仅当
 ,
, 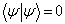 。 (5.3.3)
。 (5.3.3)
 (5.3.4)
(5.3.4)
倒三角是一个算符,意思是分别对ψ(x,y,z)的x,y,z坐标求偏导的平方和, ▽2ψ(x,y,z)+(8π2m/h2)[E-U(x,y,z)]ψ(x,y,z)=0
http://quantway.lofter.com/post/42866f_179de26
如果我们利用某个关系函数,比如Y=F(X),代入一个X算出一个Y,又将Y作为新的X再次计算下一个Y………如此不断,这种方法在数学上称为迭代,
Clifford 几何代数的基本观点
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
http://media.open.com.cn/media_file/rm/dongshi2005/liangzilixue/E_index5.htm
选定一个力学量 表象时,就相当于选定这个希尔伯特空间的一个坐标系
表象时,就相当于选定这个希尔伯特空间的一个坐标系
§5.3.1 左矢(bra)和右矢(ket)
我们知道,矢量之间的内在关系,例如两个矢量的内积或叉乘,不是必须用坐标系才能表达。很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中,一个体系的任一个状态波函数  都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基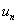 上的分量
上的分量  就是这个基相应的本征值
就是这个基相应的本征值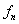 出现的概率幅,
出现的概率幅,  是
是  与
与 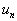 的内积
的内积 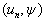 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
 都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基 就是这个基相应的本征值
就是这个基相应的本征值 是
是  与
与 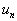 的内积
的内积 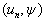 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
实际上,在讨论表象理论时,一开始用狄拉克符号方法就能够很方便简洁地导出态矢量、算符的表象及表象的变换,而不是必须从坐标表象开始。前面从坐标表象开始,仅仅是为了理解方便。
狄拉克符号是将一个体系中的任一个态矢量  用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
 用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积, 。 (5.3.1)
。 (5.3.1)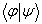 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 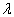 为任一复数,由上式得到
为任一复数,由上式得到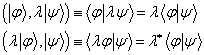 。 (5.3.2)
。 (5.3.2) , 当且仅当
, 当且仅当  ,
, 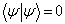 。 (5.3.3)
。 (5.3.3) (5.3.4)
(5.3.4)
式中, 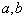 为任意常数; 若
为任意常数; 若 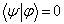 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。
[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
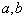 为任意常数; 若
为任意常数; 若 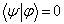 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
jpk.cust.edu.cn/lzlx/uploadimg/20075192111534.pdf
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过 ... 在数学中,一个矢量,在选定坐标系后,可. 以用它在该坐标 ... 为表述态和算符,需要在希尔轉為繁體網頁
[FLASH]体系的任何一个状态体系的任何一个状态所描写的态中测量
web.zzuli.edu.cn/picture/.../8143fe17-4886-4338-9956-f4516100b6e2.swf
这正是本章要讨论的内容,这个空间就是希尔伯特空间。 ... 选定了Q 表象就相当于选量子力学中,表象变换问题,求助- 物理- 小木虫- 学术科研第一站
emuch.net/html/201308/6207603.html
轉為繁體網頁
轉為繁體網頁
2013年8月6日 - 20 篇文章 - 4 位作者
说简单一些,即是选定了表象,就选中了希尔伯特空间的一组基底,就是选择 ... 但是物理在不同表象中的数学形式不同,动量表象和坐标表象之间的变换是一个 ... 表示这个向量时,既可以采取直角坐标系,也可以采取极坐标系。 ... F表象中的波函数它们实际上是态矢量在力学量算符F的各个本征态矢量上的投影分量。[PPT]下载 - 欢迎来到重庆邮电大学理学院
slxy.cqupt.edu.cn/lzlx/admin/.../20101110163630581.ppt
轉為繁體網頁
前面所使用的波函数及力学量算符是以坐标这个力学量算符的本征值为变量写出它们的具体形式的。那么,是否 .... 在三维矢量空间选一组正交归一完备基 ... 选定轉為繁體網頁
[PDF]第三章量子力学中的力学量
wldz.ldxy.edu.cn/lzlx/dzja3.pdf
轉為繁體網頁
在选定了一定的“坐标系”或. 称表象后,算符 ... 状态时,它的力学量,如坐标、动量、轉為繁體網頁
量子力学表象及其互换_百度文库
wenku.baidu.com/view/9cc8e3f9fab069dc502201ac.html - 轉為繁體網頁
2011年10月8日 - 在数学中,一个矢量,在选定坐标系后,可以用它在该坐标系中的一组分量来表示 ... 学中, 在量子力学中,态和力学量的具体表达方式称为表象。 ... 描述同一个状态, 是这个状态在坐范围内测量粒子动量的几率。ψ ( x, ..... 基矢上的投影即矢在希尔伯特第1章 量子理论的实验基础 从17世纪到19世纪末
media.open.com.cn/media_file/rm/.../chapter5/5_6.htm
轉為繁體網頁
很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中, ... 在选定一个力学量 表象时,就相当于选定这个希尔伯特空间的一个坐标系。轉為繁體網頁
第四章矩阵力学基础(Ⅱ)——表象理论_0x94文档库
www.0x94.com/doc/0NWp2ug3OLXjs67Zx.html
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过将正则 ... 在给定表象,即给定希尔伯特空间的一组基底后,算符用矩阵表示。 ... 在数学中,轉為繁體網頁
倒三角是一个算符,意思是分别对ψ(x,y,z)的x,y,z坐标求偏导的平方和, ▽2ψ(x,y,z)+(8π2m/h2)[E-U(x,y,z)]ψ(x,y,z)=0
http://quantway.lofter.com/post/42866f_179de26
如果我们利用某个关系函数,比如Y=F(X),代入一个X算出一个Y,又将Y作为新的X再次计算下一个Y………如此不断,这种方法在数学上称为迭代,
Clifford 几何代数的基本观点
||
高斯认为:曲面上的曲线微分长度平方、曲面上曲线的弯曲量度(曲率)是曲面上的任意曲线的基本度量量,具客观性。这是物理性的,为整个曲面几何理论的要素。这里,最小的几何单位是微元曲线、及两条正交微元曲线所形成的微元面。这个几何是没有点概念的。因为点是空(0长度,0面积)。
Clifford 几何代数的基本观点就是:物理上有意义的流形变换是保证上面的两类量的客观不变性。
音乐快递:"投影取值测度" - 由marketreflections发表- 文学城
bbs.wenxuecity.com › 论坛 › 音乐快递
轉為繁體網頁
2010年6月12日 - Von Neumann的那个年代,而是从传统“投影取值测度”(PV,又称“谱测度”)推广到“轉為繁體網頁
http://media.open.com.cn/media_file/rm/dongshi2005/liangzilixue/E_index5.htm
选定一个力学量
 表象时,就相当于选定这个希尔伯特空间的一个坐标系
表象时,就相当于选定这个希尔伯特空间的一个坐标系
§5。3 狄拉克符号
 。 (5.3.1)
。 (5.3.1)
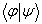 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 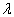 为任一复数,由上式得到
为任一复数,由上式得到
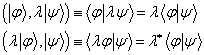 。 (5.3.2)
。 (5.3.2)
 , 当且仅当
, 当且仅当
 ,
, 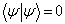 。 (5.3.3)
。 (5.3.3)
 (5.3.4)
(5.3.4)
§5.3.1 左矢(bra)和右矢(ket)
我们知道,矢量之间的内在关系,例如两个矢量的内积或叉乘,不是必须用坐标系才能表达。很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中,一个体系的任一个状态波函数  都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基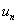 上的分量
上的分量  就是这个基相应的本征值
就是这个基相应的本征值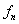 出现的概率幅,
出现的概率幅,  是
是  与
与 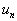 的内积
的内积 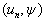 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
 都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量
都可以看作相应的希尔伯特空间中的一个矢量。在选定一个力学量  表象时,就相当于选定这个希尔伯特空间的一个坐标系。
表象时,就相当于选定这个希尔伯特空间的一个坐标系。  的本征矢
的本征矢  就是这个希尔伯特空间的基。态矢量在各个基上的分量
就是这个希尔伯特空间的基。态矢量在各个基上的分量  就组成了这个状态在
就组成了这个状态在  表象时的状态波函数(一个列矩阵)。态矢量在一个基
表象时的状态波函数(一个列矩阵)。态矢量在一个基 就是这个基相应的本征值
就是这个基相应的本征值 是
是  与
与 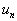 的内积
的内积 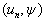 。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
。由这些可见,作为希尔伯特空间元素的态矢量的性质与传统矢量的性质是一样的。因此就可以如同一般矢量那样,用与具体表象无关的方式描述态矢量。通用的方法就是狄拉克(Dirac)构造的狄拉克符号方法(bra及ket是单词bracket的分拆)。其优点是,由于与具体表象无关,所以运算简洁。
实际上,在讨论表象理论时,一开始用狄拉克符号方法就能够很方便简洁地导出态矢量、算符的表象及表象的变换,而不是必须从坐标表象开始。前面从坐标表象开始,仅仅是为了理解方便。
狄拉克符号是将一个体系中的任一个态矢量  用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
 用相应的一个所谓右矢
用相应的一个所谓右矢  来表示。这里
来表示。这里  应理解为与具体表象有关的波函数,而写为
应理解为与具体表象有关的波函数,而写为  时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为
时就是与具体表象无关的右矢量,二者有对应关系,但绝不相等,因为  是一个与具体表象无关的抽象的态矢量,而
是一个与具体表象无关的抽象的态矢量,而  是与具体表象有关的态矢量,是
是与具体表象有关的态矢量,是  的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积,
的具体表达式。由于态矢量满足叠加原理,相应的右矢也满足叠加原理,因而右矢的线性组合仍是一个右矢。所有的右矢及零右矢形成了一个右矢空间。对任两个右矢可定义它们的内积, 。 (5.3.1)
。 (5.3.1)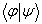 是一个复数。对于归一化的右矢,
是一个复数。对于归一化的右矢,  。设
。设 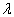 为任一复数,由上式得到
为任一复数,由上式得到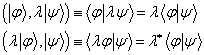 。 (5.3.2)
。 (5.3.2) , 当且仅当
, 当且仅当  ,
, 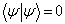 。 (5.3.3)
。 (5.3.3) (5.3.4)
(5.3.4)
式中, 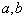 为任意常数; 若
为任意常数; 若 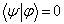 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。
[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
【精品文档】量子理论基础中的疑难问题及open问题
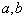 为任意常数; 若
为任意常数; 若 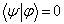 ,则称
,则称  与
与  两个态矢是相互正交的。
两个态矢是相互正交的。[PDF]第四章矩阵力学基础(Ⅱ)——表象理论
jpk.cust.edu.cn/lzlx/uploadimg/20075192111534.pdf
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过 ... 在数学中,一个矢量,在选定坐标系后,可. 以用它在该坐标 ... 为表述态和算符,需要在希尔轉為繁體網頁
[FLASH]体系的任何一个状态体系的任何一个状态所描写的态中测量
web.zzuli.edu.cn/picture/.../8143fe17-4886-4338-9956-f4516100b6e2.swf
这正是本章要讨论的内容,这个空间就是希尔伯特空间。 ... 选定了Q 表象就相当于选量子力学中,表象变换问题,求助- 物理- 小木虫- 学术科研第一站
emuch.net/html/201308/6207603.html
轉為繁體網頁
轉為繁體網頁
2013年8月6日 - 20 篇文章 - 4 位作者
说简单一些,即是选定了表象,就选中了希尔伯特空间的一组基底,就是选择 ... 但是物理在不同表象中的数学形式不同,动量表象和坐标表象之间的变换是一个 ... 表示这个向量时,既可以采取直角坐标系,也可以采取极坐标系。 ... F表象中的波函数它们实际上是态矢量在力学量算符F的各个本征态矢量上的投影分量。[PPT]下载 - 欢迎来到重庆邮电大学理学院
slxy.cqupt.edu.cn/lzlx/admin/.../20101110163630581.ppt
轉為繁體網頁
前面所使用的波函数及力学量算符是以坐标这个力学量算符的本征值为变量写出它们的具体形式的。那么,是否 .... 在三维矢量空间选一组正交归一完备基 ... 选定轉為繁體網頁
[PDF]第三章量子力学中的力学量
wldz.ldxy.edu.cn/lzlx/dzja3.pdf
轉為繁體網頁
在选定了一定的“坐标系”或. 称表象后,算符 ... 状态时,它的力学量,如坐标、动量、轉為繁體網頁
量子力学表象及其互换_百度文库
wenku.baidu.com/view/9cc8e3f9fab069dc502201ac.html - 轉為繁體網頁
2011年10月8日 - 在数学中,一个矢量,在选定坐标系后,可以用它在该坐标系中的一组分量来表示 ... 学中, 在量子力学中,态和力学量的具体表达方式称为表象。 ... 描述同一个状态, 是这个状态在坐范围内测量粒子动量的几率。ψ ( x, ..... 基矢上的投影即矢在希尔伯特第1章 量子理论的实验基础 从17世纪到19世纪末
media.open.com.cn/media_file/rm/.../chapter5/5_6.htm
轉為繁體網頁
很多情况下,不用坐标系表达两个矢量之间的内在关系可能是更方便的。在量子力学中, ... 在选定一个力学量 表象时,就相当于选定这个希尔伯特空间的一个坐标系。轉為繁體網頁
第四章矩阵力学基础(Ⅱ)——表象理论_0x94文档库
www.0x94.com/doc/0NWp2ug3OLXjs67Zx.html
轉為繁體網頁
引言: 在上一章中我们讨论了力学量的算符表示以及算符的运动方程。通过将正则 ... 在给定表象,即给定希尔伯特空间的一组基底后,算符用矩阵表示。 ... 在数学中,轉為繁體網頁
【精品文档】量子理论基础中的疑难问题及open问题
1 [ ] 2 量子测量理论是量子理论的基础支柱。它联系着理论计 算和实验测量,是两者之间的必经桥樑。按现在文献情况 可以说,不熟习量子测量理论就难以很好地理解许多近代 重要的实验工作。更何况,量子测量理论本身就蕴含着量 子理论几乎全部的未解决重大基本问题。这些问题都如此基 本,以致于它们的解答必定会从根本上纠正我们现有的时空 观念和某些基本概念,导致我们对世界有一个崭新的再认 识。 鉴于我国量子力学教材中很少谈及测量问题,所以这里 全面简要地介绍了量子测量理论。共分4讲:包括扼要介绍 测 量公设,阐述量子测量的基本要义,介绍量子光学的实验基 础,广义量子测量和POVM,测量带来的量子效应,无破坏 测量,退相干的测量模型,最后指明一些未解决问题。讲解 重点在于阐述和分析物理概念,以及明确近代量子测量理论 的认知边界。 3 目 录 一,量子力学的第三公设——测量公设 五大公设中的测量公设,初步分析 二,测量理论的三个阶段──姑娘出嫁: 纠缠分解 波包塌缩 初态制备 三,深邃的塌缩阶段——具有四大特征: 随机性 斩断相干性 不可逆性 空间非定域性 四,Von Neumann正交测量模型 模型 一个典型例算——Stern-Gerlach装置 4 五,广义测量——POVM 1, 开放系统与不完备描述 2,广义测量的物理概念 3,局域测量——POVM(正值算符测度) 1)直和子空间解释 2)直积子空间解释 3)POVM举例 六,量子测量分类 局域测量、关联测量、联合测量 开放系统测量 七,量子测量的物理效应之一——量子Zeno效应 参考文献 5 一,量子力学的第三公设 一,量子力学的第三公设—— ——测量公设 测量公设 非相对论量子力学的五大公设 量子状态公设 量子算符公设 量子测量公设(平均值公设) 量子运动方程公设 全同性原理公设(?) 6 第三公设——测量公设 “对状态 进行力学量A 的测量,总是将 按A 所 对应算符 的正交归一本征函数族 展开: 单次测量所得A 的数值必随机的属于 本征值中的某一个 (除非 是它的某个本征态);测量完毕, 即相应 突变(塌缩)为该本征值 的本征态 。对大量同样态构 成的量子系综多次重复实验时,某本征值 出现的概率是 此展式中对应项系数的模平方 。即有 对系综多次重复测量的统计平均值为 ” ψ x ˆ A ˆ i i i i A = a , i i i i ψ x = c x k a k a k x 2 k c ˆ A k a ψ x i x ψ x ψ x 2 2 2 , , , 1 1 2 2 i i 1 1 1 2 2 2 i i i ψ x a , x , a , x , , a , x , ψ x a , x c , a , x c , , a , x c , 2 2 2 1 1 1 1 1 1 2 2 2 1 1 1 c a + c a + + c a + A= c + c + + c + 7 注意1:单次测量所得力学量的数值必为本征值。单次 测量不可能得到本征值之外的数值。 量子测量必为本征值测量! 注意2:单次测量所得力学量的数值究竟为哪个本征值, 是或然的,理论事先无法预测。迄今无任何迹象显示, 测量过程的或然性是由某种隐变数所决定。量子测 量过程体现了“上帝玩掷骰子”! 注意3:除非本征态,否则,测量完毕后,态即不可逆 地塌缩(投影)到相应本征态上!多次测量时,不同塌 缩之间互相不干涉。 注意4:若对同一个态进行不同种类的测量,将会导致 不同种类的塌缩,从而表现出不同样的实验现象! 注意5:(测量导致的)量子塌缩,以及(体现在量子 干涉中的)量子叠加都是“概率幅的塌缩”和“概率幅 的叠加”!不同于宏观的概率叠加。 8 这种“概率幅的塌缩”和“概率幅的叠加”完全不同于经 典 的概率叠加。它们在测量中所表现出的或然性也完全不 同于经典概率叠加在测量中所表现出的或然性。 比如 按量子力学,沿Z轴测此态自旋,肯定发现自旋在+Z方向,并 且右边的分解是振幅叠加、相干叠加;但按经典力学,右边应 理解为以或然的方式(各有1/2概率)处在态 和 态。 由 此接着进行下面分解 又可知,如进一步测 态可得自旋朝上、朝下各1/2概率, 测 也如此。综合起来,经典力学认为:沿Z轴测得自旋朝 上朝下的概率应当各占1/2!这与上面量子力学结果完全不同! 1 + z = +x + -x 2 1 +x = +z + -z 2 1 -x = +z - -z 2 +x -x + x -x 9 二,测量理论的三个阶段─ 姑娘出嫁: 纠缠分解;波包塌缩;初态制备 量子体系状态改变的两种方式──量子理论的两种因果观: U 过程──决定论的、可逆的、保持相干性的 R 过程──随机的、不可逆的、斩断相干性的 有人用U 过程代替R 过程。这种思路是不正确的。 理想的完全测量的三个阶段──姑娘出嫁 纠缠分解 波包塌缩 初态制备 “纠缠分解”:ψ(r)按被测A本征态分解并和测量指示器可区分态纠缠; “波包坍缩”:ψ(r)以A展式系数模方为概率向本征态之一随机突变; “初态制备”:坍缩后态作为初态在新环境哈密顿量下开始新一轮演化。 实验经常对大量相同量子态所组成的量子系综进行同类重复测量并读出 结果。多次重复测量将制备出一个混态──不同塌缩得到的φ i (x)之间不存 在任何位相关联,彼此是非相干的。这个混态也称做纯态系综──一个纯态 系列:{出现纯态φ 1 (x)的概率为p 1 ; 等等} 10 三,深邃的塌缩阶段─具有四大特征 随机性 斩断相干性 不可逆性 空间非定域性 状态塌缩过程是一个极其深邃的、尚未了解清楚 的过程。 其中存在一系列根本性的open问题。 塌缩过程的四大特征 按测量公设,每次测量并读出结果之后,态ψ(r)即受严重干扰,并 且总是向该次测量所得本征值的本征态突变(塌缩)过去,使波函数约化 到它的一个成分(一个分枝)上。这种由单次测量造成的塌缩称为第一类 波包塌缩。除非ψ(r)已是该被测力学量的某一本征态,否则在单次测量 后,被测态ψ(r)究竟向哪个本征态塌缩,就象测得的本征值一样,是随机 的、不能事先预计的。 随机的──原则上就无法预见和控制的 不可逆的──有人说,测量是熵增加过程 切断相干性的──切断被测态原有的一切相干性 非定域的──波函数的塌缩总是非定域的 11 塌缩中,表现出是粒子状态的突变,实质 上是体系演化时空的塌缩! 近来实验表明:塌缩与关联塌缩是同一个 事件,其间不存在因果关联! 塌缩中存在的未解决的问题: 塌缩随机性的根源是什么?──或者有根源吗?! 为什么(不论自旋态或空间态、单粒子或多粒子) 所 有塌缩过程总是非定域的? 塌缩过程中微观体系的熵真的增加了? 塌缩——关联塌缩和相对论性定域因果律有没有深 刻 的矛盾?!认为是同一个事件就能解决问题吗? 相互作用过程和测量过程的明确界线? 12 Von Neumann 为了测量子系统可观测量A,要建立“测量哈密顿 量 ”。办法是接通子系统可观测量A 和(作为测 量仪器的)指示器X 。在A-X 之间存在某种耦合, 它在可观测量本征态和指示器的可区分态之间建立起 量子纠缠。正是这种量子纠缠,使我们能够通过测量 指示器变数x 去制备可观测量a 的本征态。 设初始时刻子系统处于A的一个叠加态 , 而指示器波包有关变量的状态为 。合成的大系统 处于尚未纠缠的可分离态, i i i a c i H x x a c x i i i 13 由于 中A 和X 的耦合项存在,在t 时刻 后,这个量子态将从可分离态演化成为纠缠 态, 所造成的量子纠缠使X 和A 的测量值x (和a)关联起来。如果位置变量x 的观测 精度足以分辨的全部本征值a ,就实现了通 过测量,造成可区分态塌缩并得到 造成 可观测量态的关联塌缩并得到相应本征态 和数值 。 t a x x t a x a c x a c t U i i i i i i i i i , i H i x i a i a i H 14 ——Stern-Gerlach 测 自旋粒子的 ,使它通过z 轴方向为非 均匀磁场 。粒子磁矩 ,它和磁场之间的耦 合项(“测量哈密顿量”)为 这里是可观测量 和位置 相耦合。由于 中 含 ,不同 值处附加能数值不同,这产生一个 力沿 轴,正负视 而定。在测量(穿过磁场) 时间 内给粒子冲量 1 2 z z B = λz μσ z H = -λμzσ z z z H z H F = - = λμσ z z σ = 1 z P = F t z t z 15 这就是说,耦合使指示器(z方向的位置)偏 转。通过观察粒子向 z 轴正向、反向的偏转 距离,投影出粒子自旋态 或 。 这里 。注意,此处仍有 1 1 1 1 0 i i i i i h i i t U 位置指示 位置指示 z z exp exp exp z z i i i U t z t F t z P z m t F t m P z z i 2 2 z p z p m p m p t E z z z z 16 五,广义测量——POVM 1, 开放系统与不完备描述 这时的量子力学出现三个新特点: a)量子态可能是混的; b)量子演化可能是非幺正的、不可逆的; c)量子测量造成的投影分解可能是非正交的分解— POVM 2,广义测量的物理概念 孤立系正交投影测量 子体系的广义测量 广义测量,又称为局部测量。它是指,在一个由若干子系统 组成的大系统上进行正交测量时,在某个子系统上所实现的 片面性测量。由于子系统是个开放系统,广义测量也可说成 是对开放系统的量子测量。 一般在大系统上进行的正交投影测量,折射到子系统上 就成为对子系统的片面观测、局部观测、局域观测。 17 如果计入所有与此子系统有相互作用的外部系 统,构成足够大的系统,总能以足够好的近似将这 个大复合系统看作孤立系。对此大系统中某组相互 对易力学量完备组进行量子测量,必定是正交投影 测量。测量所得必是这个完备组共同本征态的量子 数,测量所实现的也必定是向这个完备组共同的相 互正交本征态族的随机投影。 但是,大系统相互正交本征态族在子系统所属 子空间的对应态未必仍然相互正交!设想根本就不 知道(或是不想知道,或是难以知道)大系统、只 知道子系统的观察者,会认为:普遍的量子测量将 投影出一组非正交态,而不是一组正交态。这就是 常说的“广义测量不一定是正交投影”的原故。 3, 局域测量——POVM(正值算符测度) 18 1)直和子空间解释 假设考虑的态空间 是一个更大的直和空间 的一部分。设 是 的一个可观察量,有正交分解关系 注意,虽然不同 值的 彼此正交,但它们在子空间中投影 部分 却不一定彼此正交,也不一定归一。但由于 记 。注意 均不会为负值。于是可令 由此,这里态 已归一。现在假设,在大空间中对子空间 的态 执行正交投影测量 。这些测量从“生活” 在 中的观察者来看,只得到以概率( 不属 ,作用为零) 获得测量结果 和态 。特别是,塌缩投影过去的这些测量 末态 不见得彼此正交。 A H A H = H H A H A M 0 A A M M ~ ~ u α u ~ 1 u u ~ ~ 1 α λ ~ α α α E = u u A H A ρ A ρ H α A α α A α α α A α Prob α = u ρ u = ψ ρ ψ = λ ψ ρ ψ α ψ ; ; : : : A α H i H μ i μ = 0, i, μ H u α ψ 19 设 是子空间 的单位算符,它也是大空间 向子空间 的投影算符。于是利用它可将中的正交投影算符系列向投 影。即定义 中的一组算符 利用此定义式,可以把上面观察所得结果为的概率重新写为 这些 是厄密的、非负的,但迹却不一定为1( ) 而且也不一定彼此正交,所以不能算是正交投影算符系列。 然而它们总和等于子空间的单位算符 因此,这些在子空间中执行着类似于在大空间中的投影分解 任务,但它们却不是正交投影。于是推广开来看,引入 定义:系统A的一组POVM{positive operator valued mesure}是 一组能对A的单位算符进行分解的非负厄密算符系列: 这里态 是系统A的任意态。 A H A A E = I A H H ~ ~ E E E F A A A A A F tr ob ~ ~ Pr F 0 1 TrF A A A A I E E E E F n A A A I F F F F n F 1 ; , 0 ; ; , , 2 , 1 , A F 20 根据这里的广义测量理论,当对中态作广义测量时,相应每 个测量结果 的概率由上式表示。特别是,有 为保证概率正定和总概率为1, 的正定性和 都是必需 的。由于任何投影算符的平方等与它自己,所以开根也是它 自己。于是对投影算符 ,广义测量前后态的改变 此式是正交投影情况 向POVM情况的推广。注意,由于“ 等于大空间的 向子 空间 的投影”,所以有 的维数目 数目 数目= 维数和 个数可能少于 个数的原因是:可以有这样的 ,它只向 正交子空间 投影,于是与这种 相应的 便是零。 F F Pr A ob tr F 1 F α α α F = ψ ψ F F A A A A A A α A α α ρ ρ = E ρ E A H α F α E A H = H + H F α E α E H F α E F α E A H 21 2)直积子空间解释 考虑一个 维系统A,处在态 上。并假设另有一个辅 助系统B(常称为“附属系统”,其维数这里并不重要,予 以 略去)处在已知态 上。设这两个系统组成一个“未关联” 的 张量积大系统,初态为 。现在对这个张量积系统 进行某种正交投影测量 。在单次测量中得到测量 结果为 中的某一个,相应概率为 简单直接地说,即有 这里 这一组算符 就被称作为一组POVM——正值算符测度。这 里, 既是张量积大系统在正交测量中得到结果 的概 率,也是在子系统A中执行相应POVM并得到 的概率。 A B B A AB AB I E E ; E N N n m A A nm A mn N n m s r sr B nm A ns mr B A AB F Tr F E E Tr ob 0 , 0 , , , Pr A A B A AB F Tr E Tr ob Pr mn B A B s r sr B ns mr mn I E Tr E F , , F ob Pr E F 22 由于 ,以及 任意和非负的,可知全体 都是非负的,有时就简单称它们为正的。按上式,它们 也是厄米的、总和为1。后者为对 求和即得,分量形式 为 这正是对 的单位分解。但对于直积情况,POVM中 个 数的上限与直和情况不同。这时有 维数积 当对大系统 测量之后,塌缩结果为 时,大系统的 态相应塌缩到下面状态, 但与此同时,对于只知道子系统A的观察者而言,当测量 塌缩到 时,密度矩阵变化为 A I 0 Pr ob A F mn A mn B B mn s r s r sr B rs mn sr B ns mr mn mn I Tr E F F , , , μ F B A A H H E Number F Number H dim dim B A E B A AB B A AB E Tr E E F B A B A A AB A B Tr E E Tr E 23 3)POVM举例——单qubit两维态空间中的POVM 选择N个3维单位矢量 和N个正实数 ,使它们满足: 由此便可构造一组N个元素的POVM: 这里 是态的极化矢量。 自旋态的投影算符和 关系为 共计N个,都是非负的、厄密的,并且 。 这N个 就在此qubit二维态空间中定义了一个POVM。 注意,在两维态空间中作单位算符POVM分解时,若是两个分 解,分解虽有无穷多种,但必定都是正交的: 只有多于所在空间维数的分解,即 的分解,才必定是非正 交分解。比如N=3,若取任意三角形的三个边作为(首尾相接 的)三个矢量 ,有 ,再选比如 ,便 得到一组三个如下POVM, 。由乘积知, 它们已不再是正交投影,各自迹也不是1。 α α α F = λ 1+n σ 1 2 α α λ = 1 n 0 n α α α α 1 E = n n = 1+ n σ 2 I n I F α α α F = 2λ E F 2 1 F F n n n n I ) 3 , 2 , 1 ( n 0 3 2 1 n n n 3 1 3 2 1 3 , 2 , 1 ; 3 2 1 3 1 n E n F 3 N n α α F E α 0 < λ < 1 24 另一个在三维执行正交投影在两维观察的POVM例子。 设有Descartes坐标架转动 这里 。其中 为三个Euler角, 为矢 量表示的三个角。于是有 现执行一个向二维空间的投影,即以投影算符P 作用,得三 个POVM如下 R αβγ 1 , 2 , 3 = 1 , 2 , 3 R R 3 2 1 2 3 i i =1 1 2 3 Φ = c 1 + c 2 + c 3 , c = 1 1 0 0 1 1 2 2 3 3 = I = 0 1 0 0 0 1 E = 1 1 , E = 2 2 , E = 3 3 , i i F = PE P = P i i P , i = 1,2,3 25 六,量子测量分类 ■ 以往量子力学常只研究 孤立、封闭量子体系 此时量子测量都是 von Neumann 正交投影——按测量 公设,是向被测力学量的本征函数族投影: i.e., ■ 量子测量,按不同情况和不同分类标准,有不同分类: i) 封闭系统的量子测量与开放系统的量子测量; ii) 两体及多体有局域测量、关联测量、联合测量; iii) 完全测量与不完全测量。 。 1 , , , , i j ij j i i i i i trE E E E I E i i E E , , , , 1, 2, 3, i i ij E E i i i j i j 26 ■ 两体局域测量、关联测量、联合测量 1)局域测量:只对两体中的某一方作测量,比如只对A 测量。相应力学量是 所有测量结果只和约化密度矩阵ρ A 有关。 2)关联测量:同时对A 和B 作局域测量(并比较相应 的结果): 此时只对未纠缠态——可分离态,有 3)联合测量:测量不是局域进行的,类似于下面不可 分离类型的力学量测量 B A I A A A r A AB B r A r B A AB B r A r AB r T T T I T T T B A B A 2 , i i i B i A 27 ■ 开放系统测量 出现三个新特点: 1)态可能是混的; 2)演化可能是非幺正的、不可逆的; 3)测量可能是非正交投影分解—POVM POVM ──正算符取值测度 POVM是(针对封闭系统的von Neumann正交投影理论) 向开放系统的推广,是完全测量向非完全测量的推广。 大系统进行正交测量时,在子系统上实现的测量称为广 义测量。 1 , , , a a trF F I F F F F 之间不一定正交, 不同 28 七,量子测量的物理效应之一——量子Zeno效应 11))原以为是量子Zeno佯谬 初始以为是个量子力学的佯谬——Zeno佯谬; 2)量子Zeno效应——“量子水壶效应” 现为一个地道的纯量子效应——量子Zeno效应, 理论研究发现,频繁地对一个不稳定系统进行量子测量 会抑制或阻止它的衰变(跃迁)。极端而言,连续的量子测 量将使不稳定系统稳定的保持在他的初态上,完全不发生衰 变或跃迁。这种不稳定初态的存活几率随测量频度的增加而 增加的现象就是量子Zeno效应。 “量子水壶效应”——越看越烧不开的的““量子水壶 量子水壶””。。 3)量子Zeno效应存在性的理论论证 ii))分两步证明。先证: 任何含时量子系统初始的衰变速率必为零。 含时量子系统问题的类型和相关计算尽管都很复杂,但此结 论却是一个共同的结论。 29 含时系统问题可普遍化地提为 定义: 定义:任意不稳定量子系统,演化到t时刻,初态仍存活着而不衰变(不 跃迁)的几率为 P(t)=|<ψ(0)|ψ(t)>| 2 命题:任何不稳定量子系统的初始衰变(跃迁)速率必定为零。 证明(1):由于 于是 令t→0,取极限,即得 这是量子力学中具有普遍性的结论之一, 当然也是各类含时微扰论的共同特征。 t =0 d | ψ(t) > i = H(t) | ψ(t) > dt | ψ(t) >| =| ψ(0) > d | ψ(t) > 1 d < ψ(t) | 1 = H(t) | ψ(t) >, = - < ψ(t) | H(t) dt i dt i dP(t) d = ψ(0) ψ(t) ψ t ψ 0 + h.c. dt dt 1 1 = ψ(0) H(t) ψ(t) ψ t ψ 0 - ψ 0 ψ t ψ(t) H(t) ψ(0) i i t =0 dP t = 0 dt 30 ii) 第二步论证。用测量公设中测量必将制备初态。 设一个含时量子系统初态为|ψ(0)>。由一般分析可以知 道,随着这个不稳定系统的演化,其初态的存活几率 将越来越小。 当然,这个P(t)按其物理含义应当只适用于:自t=0开始 演化之后,直到t 时刻才执行初态存活与否的量子测量(假 设测量是理想的瞬间完成的,以下同此),在(0,t)时间间隔 内不再另行插入这类测量。 现在问:如果在(0,t)之间再插入N 次这类量子测量,相 应的初态存活几率P N (t)实测值会不会发生变化?下面根据量 子测量理论所作的分析表明: P N (t) 的数值随N 增加而增加。 证明(2):将[0,t]区间等分成N份,在每一时刻t n =nt/N进行一 次量子测量,以确认体系是否仍在|ψ(0)>上。按上面关于P(t) 含义的叙述,在t/N时刻的第一次测量时,初态存活概率为 P(t/N) 2 P t = ψ 0 ψ t 31 按测量理论,除衰变或跃迁的已经不予记入了以外, 剩下的这P(t/N)部分将塌缩成为初态|ψ(0)〉,并以此时刻 t/N 为初始时刻,再次重新开始演化。演化到2t/N时刻,再 次作类似测量。于是,经上一次测量后,到2t/N 时刻又作 第二次测量时,初态存活几率为 P 2 (t/N) 如此继续,在[0,t]内经受(N-1)次测量后,到t 时刻作第N 次 测量时,初态|ψ(0) 〉的存活几率将成为 P N (t)=[P(t/N)] N 。 当N 足够大时t/N 足够小,可将P N (t) 展开: t t t N N N P = P 0 + P 0 + = 1+ P 0 + 32 令N —>∞,就过渡到在[ 0, t ]内连续测量极限情况 ——理想的连续测量情况。设这时存活几率为P c , 注意 ,最后得到 P c =1 即: 当不稳定体系经受连续量子测量时,将会 一直呆在它的初态上,而不发生(本应发 生的)衰变或跃迁。 *Zeno效应的原来证明见:B. Misra and E. C. G. Sudarshan, J. Math. Phys., 18(1977)756, 但证明十分繁复;这里简洁普适证明取自:Y. D. Zhang,et.al., Some studies about quantumZeno effects, included in 〈Fundamental problems in quantumtheory〉, edited. by D. M. Greenberger and A. Zeilinger, Annals of the New York Academy of Sciences, Vol. 755, 353(1995). 实验证实之一:W. M. Itano, et.al., PRA,41(1990)2295; 1989年美国家标准和技术所, 〈时间之箭〉, p.130;稳定核内的中子不衰变,至少有此因素。
No comments:
Post a Comment