廣義相對論入門[编辑]

维基百科，自由的百科全书
跳转至： 导航、 搜索
由卡西尼-惠更斯号空间探测器完成的对广义相对论的高精度的演证：在地球和探测器之间传输的无线电信号（绿色的波）因为太阳的质量造成的时空（蓝色的线）弯曲而延迟。
广义相对论是一个关于引力的理论，它在1907年到1915年由爱因斯坦完成。根据广义相对论，物质之间的引力来自于时空的弯曲。
在广义相对论出现之前的200多年间，牛顿万有引力定律被广泛接受，它成功地解释了物质之间的引力作用。牛顿的定律中，引力来自大质量物质之间的相互吸引。虽然牛顿也不知道这个力的本质，但它在描述运动时却非常成功。
但是，实验和观测都显示，爱因斯坦对引力的描述能够解释多个由牛顿定律无法解释的现象，比如水星和其他行星轨道的反常的进动。广义相对论还预言了一些关于引力的显著效应，比如引力波和引力透镜，还有引力场引发的时间膨胀。很多预言都已经被实验所证实，还有一些正在探索中。比如，引力波存在的直接证据仍然没有找到，有一些科学家正在为此做实验，如LIGO和GEO 600项目。
广义相对论已经成为现代天体物理学的重要工具。它提供了现在理解黑洞（一个引力强大到使光都无法逃逸的空间区域）的基础。其强大的引力也使一些天体发出强烈的辐射（比如活动星系核和X射线双星）。广义相对论也是宇宙学的大爆炸模型的一部分。
然而，到现在仍然有大量的问题没有解决，其中最根本的是广义相对论如何和量子力学结合而产生一个完整一致的量子引力理论。

目录

 [隐藏] 

从狭义到广义[编辑]

1905年，阿尔伯特·爱因斯坦发布了他的狭义相对论，描述了物体在惯性参考系下的行为，使得牛顿运动定律能够和电动力学（电荷載子之間的相互作用）相结合。狭义相对论为物理学制造了一个全新的框架，它完全改变了时间和空间的概念。然而，当时被广泛接受的一些物理学理论与那个框架不兼容，其中最重要的是描述了物体之间由于质量而相互吸引的牛顿万有引力定律。
那时候包括爱因斯坦在内的一些物理学家都在寻找一个能够将牛顿的引力理论和狭义相对论相结合的新理论。但是众多理论中，只有爱因斯坦的理论最终被实验和观测所证明。为了理解理论的核心概念，最好沿着爱因斯坦在1907年到1915年的思路一起思考，从他的思想实验到几何化的引力理论。 [註 1]

失重和惯性参考系[编辑]

设想一个处在自由下落的电梯中的人，在下落过程中人处于失重状态，他周围的物体也将漂浮在空中，或者作匀速直线运动。然而，在太空中没有引力的地方（即一个惯性参考系；惯性参考系里的现象能够用狭义相对论解释），他周围的物体也会是同样的现象——静止，或者匀速直线运动。显然，一个观察者不能区分自己是在自由下落的电梯中，还是在太空中没有引力的地方。[註 2]
处于失重状态的观察者和在惯性参考系中的观察者所观测到的现象是相同的，爱因斯坦认为这是引力的基本原理，并称它为等效原理。这就是广义相对论的基础。粗略地讲，这个原理规定一个自由下落的电梯中的观察者无法说明他们正在自由下落，因为在这里做的任何实验都和在远离所有引力场的太空中有相同的结果。[註 3]

引力和加速度[编辑]

在一个加速上升的火箭中(左)和在地球上(右)小球掉落的情况
就像大部分由引力产生的现象可以通过做自由落体运动而消除（即失重），由引力产生的现象也可以通过让物体处于加速运动的参考系而产生，任何由加速运动而产生的现象同样可以用等价的引力场来解释。一个在封闭房间中的观察者无法区分下列现象哪一个是正确的：
  • 物体会掉到地上是因为这个房间处于地球表面，物体被地球的引力拉到地上。
  • 物体会掉到地上是因为这个房间在一个远离其他星球的火箭中，火箭正在以9.81米/秒2的加速度上升，物体因为惯性力而掉到地上。
爱因斯坦利用等效原理预言了一些关于引力的物理现象，这将在下一部分解释。
一个处于加速运动的参考系中的观察者可以用惯性力来解释他所感觉到的加速度。例如，有一个力作用在加速运动的汽车的司机身上，将他推向他的座位；当你旋转你的手臂使它做圆周运动时能够感觉到一个力将你的手臂向外拉。爱因斯坦认为：来自地球的引力场的力在根本上是和惯性力等价的。[註 4]因为在加速度不变时，惯性力和质量是成正比的，所以引力场中的物体也应该感受到一个正比于它的质量的力，这个力就是牛顿万有引力定律所描述的引力。
总结一下，以上两节中提到了爱因斯坦的假设等效原理，十分简略地讲：
  1. 处于失重状态下，和处于惯性参考系中，是等价的。
  2. 参考系拥有加速度，和受到引力，是等价的。

等效原理的推论[编辑]

1907年，爱因斯坦距离完成他的广义相对论还有8年时间。但是现在他已经能够根据他的理论的基础——等效原理，作出大量可以验证的预言。[註 5]
光波在向上远离下面的黄色恒星的引力场时的引力红移现象。
第一个新现象是光波的引力红移。请考虑在一个加速运动的宇宙飞船上的两个观察者。在这样的飞船上，一定有一个自然的“上”和“下”的概念：飞船加速度的方向是“上”，与之相反的物体掉落的方向是“下”。假定其中一个观察者处在另一个的正上方。当下方的观察者向上方的观察者发送了一段光信号，加速度会使光红移，上面的观察者将收到一段频率低一些的光信号。相反地，当上方的观察者向下方的观察者发送了一段光信号，加速度会使光蓝移，即频率更高。并且在已知发出频率和接收频率的情况下，可以通过狭义相对论计算出加速度。[註 6]根据等效原理，爱因斯坦认为这样的红移现象一定也可以在引力场中观察到，即，若引力场方向竖直向下，则下方的观察者收到的来自上方的光信号频率偏高，上方的观察者收到的来自下方的光信号频率偏低。左图显示了一段光波在远离引力场时的红移。这个现象已经被实验验证。
与引力红移现象对应的现象是引力时间膨胀。在一个竖直向下的引力场中，上方的观察者（处于较高的引力势）测量到的频率更低，时间也流逝得更快。相反地，更靠近引力场源的观察者处于较低的引力势，时间流逝得稍慢。其原因，极为简化地说，是我们使用光子钟作为计量标准，即测量一段时间的结果表示为光子的周期的倍数，那么当上方观察者测量到频率变低时，光子周期变大，对于同样一段时间，上方观察者所认为的这个时间相比光子周期的倍数数值，比下方所得到的数值小，那么在下方看来，对于同样一段时间，上方观察者的钟就走得慢了。然而上方观察者所得到的1秒所代表的时间，实际上比下方观察者认为的1秒要长，是所谓上方观察着的时间流逝得更快了。[1]
很重要的一点是，对于每一个观察者自身的参考系，将不会观察到时间的变慢。“五分钟”这个数值所表示的时间对于不同的观察者都是一样的；当时钟显示一年过去时，观察者的年龄也确实增长了一岁；原来处在下方的观察者，当其与上方观察者换位置后，他不会觉得两边时间流逝有什么差别。简而言之，每个钟对紧挨着它发生的事情的测量都是准确的。只有当这个钟与處於不同地方的另一個观察者的鐘比较时，才会发现靠近引力场的观察者的时间流逝得更慢。[2]
爱因斯坦还预言了光在引力场中将偏折：在引力场中，光会向下偏折。要解释这个预言需要一个更加复杂的广义相对论方程，而不仅仅是等效原理。[註 7]

潮汐现象[编辑]

两个向地球中心加速坠落的物体也在朝着对方加速靠近。
引力现象和惯性现象的等价關係并没有构成完整的引力理论。值得注意的是，它無法回答接下来的简单问题：是什么防止了世界另一边的人们掉下来？当我们回到我们在地球表面的视角解释引力时，我们注意到我们的参照系并没有自由下落。我們期待惯性力能夠提供一个合理的解释，但是在地球这边的自由下落的参照系不能解释地球另一边的人们感受到的引力方向為什麼與我们感受到的相反。
再想像两个物体肩并肩地自由下落，在一个自由下落的参照系中，两个物体应该是漂浮着处于失重状态，但是事实并非如此。这两个物体并非精确地朝向同一个方向；他们的方向是同一个点：地球的重心。所以，两个物体实际上在相互靠近。在一个小环境中（比如一个自由下落的电梯），两者之间相对运动的加速度是非常小的；但是对于地球两边的跳伞运动员来说，这个现象非常明显。力在方向上的差别造成了海洋中的潮汐，所以这被称为潮汐现象。
惯性和引力等价并不能解释潮汐现象——它不能解释引力场的变化。[註 8] 所以，我们需要一个理论来描述物质（比如地球这样大质量的物质）如何影响它周围的惯性环境。

从加速度到几何解释[编辑]

在探索等效原理和潮汐现象时，爱因斯坦发现了几个和曲面几何的类比。举例来说，从惯性参考系（自由粒子在这种参照系中总是做匀速直线运动）到转动参考系（在这种情况下必须引入惯性力来解释一些现象），这就类似于从直角坐标系到曲线坐标系（这种坐标系中坐标轴不需要是直线）的变化。
还有一个潮汐力和曲面的曲率之间的更加深入的类比。对于引力场，潮汐力的存在与否决定了引力的现象是否可以通过选择一个自由下落的坐标系来消除。相似地，曲率的存在与否决定了曲面是否等同于平面。1912年夏天，在思考了这些类比之后，爱因斯坦找到了能够描述引力的公式化几何解释。[註 9]
几何的基本对象是点、线、三角形，它们通常定义在三维空间里或者二维的曲面上。1907年，数学家赫尔曼·闵可夫斯基为狭义相对论创造了一种新的公式化的几何，因为狭义相对论中的几何不仅包括空间，还包括时间。这个新的几何的一个基本实体是四维时空。移动物体的轨迹是四维时空中的线；物体的轨迹总是做匀速直线运动。[註 10]
曲面是从平面（平整的面）到普通的弯曲的面的推广，曲面几何在19世纪已经被卡尔·高斯所描述。这种描述已经被波恩哈德·黎曼在19世纪50年代推广到更高维的空间。在黎曼几何的帮助下，爱因斯坦发现了引力的公式化几何解释，其中闵可夫斯基时空被弯曲的时空所替代，这就像从平面到曲面的推广。[註 11]
在他意识到这个几何类比的正确性之后，爱因斯坦又用了3年时间来寻找他的理论中还没有被发现的要素：描述了物质如何使时空弯曲的公式。在发现了爱因斯坦场方程后，他于1915年下半年在普鲁士科学院发表了他关于引力的新理论。[註 12]

引力和几何[编辑]

美国相对论研究的首席专家，約翰·惠勒解释，爱因斯坦的引力的几何理论可以这样概述：时空告诉物质如何运动，物质告诉时空如何弯曲。[註 13] 这句话的意思将在接下来的章节解释，接下来将要研究测试粒子的运动，调查物质的什么属性导致了引力，最后，介绍爱因斯坦的方程，它将物质的属性和时空的弯曲联系到一起。

探索引力场[编辑]

相交的测地线：两条经线（绿色）在赤道（红色）处是平行的，但却相交于极点。
为了理解一个物体的引力，我们需要先理解物理学家所说的探测器或者测试粒子：一个粒子被引力影响，但却足够小、足够轻，因而我们可以忽视它自己的引力现象。在没有其他作用力的情况下，一个测试粒子做匀速直线运动。在时空中，这意味着这个测试粒子正沿着时空中笔直的世界线移动。但是考虑了引力之后，时空就不再是欧几里得几何了，或者说是弯曲了。在这样的时空中，笔直的世界线可能并不存在。相反，测试粒子沿着测地线运动。
在大地测量学（测量地球的尺寸和形状的科学）中，测地线是连接地球表面两点的最短距离。近似地，这条线是一个大圆上的弧，比如经线和赤道。这些路径显然不是直的，因为它们沿着地球的弯曲的表面。
测地线的性质和直线是不一样的。例如，在平面中，平行线没有交点，但是地球表面的测地线却有交点，在赤道处平行的经线在极点处相交。类似地，自由下落的测试粒子的世界线是时空中的测地线。它们和狭义相对论的没有引力的时空中真正的直线之间有着决定性的区别。在狭义相对论中，平行线永远保持平行，但在有潮汐现象的引力场中，通常是不正确的。例如，如果两个物体刚开始是相对静止的，然后坠落向地球的引力场，它们会一边落向地球中心，一边相互靠近。[註 14]
与行星和其他天体相比，我们日常生活中见到的物体（人、汽车、房子、甚至山）的质量都非常小。所以我们完全可以用来描述测试粒子的定律来描述关于这些物体在地球引力场中的现象。注意，为了将一个测试粒子从测地线上移开，必须施加一个额外的力。一个坐在椅子上的人正尝试着沿着测地线运动，就是朝地球中心自由下落。但是椅子给他施加了一个额外的向上的力阻止他落下。这样，广义相对论解释了我们日常生活中在地球表面感受到的引力并非由于地球给我们的向下的力，而是由于一个额外的支持力，这些力使地球上的物体没有沿着它们的测地线运动，而是在地面保持静止。[註 15]对于那些质量很大而不能忽视它们的引力的物体，它们的运动定律要比测试粒子复杂些，虽然时空告诉物质如何运动这个定律仍然是正确的。[註 16]

引力的来源[编辑]

在牛顿万有引力定律中，引力来自于物质。更精确地说，引力来自于物质的特定属性：质量。在爱因斯坦的理论以及基于相对论的其他引力理论中，物质的存在还导致了时空的弯曲。这里，质量也是一个决定引力的重要属性，但是在相对论中，质量不是引力的唯一来源。相对论将质量和能量联系起来，而能量和动量又联系在一起。
质量和能量的等价已经通过E = mc2表示出来，这也许是狭义相对论中最著名的公式。在相对论中，质量和能量是描述同一个物理量的两种不同方法。如果一个物理系统有能量，那么它也有与之等价的质量，反之亦然。一个物体的所有属性都能联系到它的能量，比如温度或者原子、分子等系统中的结合能。所以这些属性又通过能量同质量联系在一起，综合起来形成引力。[註 17]
在狭义相对论中，能量和动量紧密联系在一起。就像时间和空间通过相对论联系在一起形成一个同一的整体，叫做时空；能量和动量联系在一起形成一个同一的四维的物理量，物理学家称它为四维动量。于是，如果能量是引力的来源，那么动量也是。对于那些直接联系到能量和动量的物理量，比如压强和张力，也影响到引力。综上所述，在广义相对论中，质量、能量、动量、压强、张力都是引力的来源。它们解释了物质如何让时空弯曲。在理论的数学方程中，这些量都是但又只是一个范围更广的物理量的一部分，它叫做应力-能量张量。[註 18]

爱因斯坦场方程[编辑]

爱因斯坦场方程是广义相对论的核心，它使用数学语言精确地描述了物质的性质和时空之间的联系。更具体地，它使用了黎曼几何中的概念和方法。在黎曼几何中，空间（或者时空）的几何性质被一个叫做度量张量的量描述。度量张量将需要的信息组织起来，并计算出弯曲的空间（或者时空）中角和距离的基本的几何概念。
不同纬度上相隔30度的经线之间的距离。
一个简单的例子是像地球表面这样的球面，球面上的任何一点可以表示成两个坐标：地理学的经度和纬度。不像平面上的笛卡尔坐标系，两点之间的距离不仅和它们坐标的差有关，还和它们的位置有关，就像右图：在赤道处（品红色线段）的人向西移动30经度经过的路程大约是3300千米，但是在纬度是55度的地方（蓝色线段）的人向西移动30经度经过的距离大约是1900千米。坐标不能提供足够的信息来描述球面上，或者说是任何更加复杂的空间和时空的几何。这些信息正是度量张量所提供的。度量张量是定义在曲面（或者空间、时空）上的所有点上的函数，并将坐标的差别于距离的差别联系起来。所有其他的和几何相关的量，比如曲线的长度，或者两条曲线相交的角度都能够通过度量张量计算出来。[註 19]
度量张量函数和它的变化率可以用来定义另一个几何量：黎曼曲率张量，它描述了空间（或者时空）在每一点处如何弯曲。在广义相对论中，度量张量和黎曼曲率张量是定义在时空的每一点上的量。就像我们已经提到的，时空中的物质定义了另一个量：能量-动量张量T，“时空告诉物质如何运动，物质告诉时空如何弯曲”的原理意味着这些量必须互相联系。爱因斯坦通过用黎曼曲率张量和度量张量来定义另一个量G来表示这种联系，这个量G现在被叫做爱因斯坦张量，它描述了时空弯曲的方式。于是，爱因斯坦场方程可以表示成：
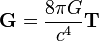
\mathbf{G}=\frac{8\pi G}{c^4}\mathbf{T}
通过几个常量，G（描述曲率）可以换算成T（描述物质的含量）。在这个方程中的常数反应了不同的理论的结合：G是在牛顿的引力理论中就已经出现的引力常数；c是光速，狭义相对论的关键；π是圆周率，最基本的几何常数之一。
方程中的G和T 又各自被几个关于时空中的坐标的函数决定，而这个方程与这些函数是等同的。[註 20]这些方程的一个解描述了一个特定的时空，例如，史瓦西解描述了像恒星和黑洞等球形的不旋转的大质量物体附近的时空，克尔解描述了旋转的黑洞。还有其他的解能够描述引力波，弗里德曼-勒梅特-罗伯逊-沃尔克解描述了膨胀的宇宙。最简单的解是狭义相对论中平直的闵可夫斯基时空。[註 21]

实验验证[编辑]

主条目：广义相对论的实验验证
没有科学理论是必然正确的；它们必须被实验验证。只要有一个实验和理论不相符，这个理论就是错误的。牛顿万有引力定律是因为它对太阳系内的行星和卫星的运动的预测都非常准确，因而被人们接受。但是，随着测量精度的不断提高，一些不符合理论预测的现象逐渐被发现了。这些不一致被广义相对论所解释了，但是广义相对论的预言依然需要被实验所检验。其中三个实验是爱因斯坦自己想出来的，现在已经成为了广义相对论的经典的验证：
行星绕恒星作公转的牛顿引力定律轨道（红）和广义相对论轨道（蓝）。
  • 牛顿的引力理论预言了单个行星绕着球形的恒星运动的轨道是椭圆，而爱因斯坦的理论预言这是一个更加复杂的曲线：行星在沿着椭圆轨道运动的同时，这个轨道本身也在绕着恒星缓慢旋转。在右图中，牛顿定律预言的椭圆轨道是红色的，爱因斯坦预言的轨道是蓝色的。对于绕太阳旋转的行星，广义相对论对此的预言和牛顿定律的偏差叫做行星轨道的进动。对水星轨道的这一现象的第一次测量早在1859就做过。到目前为止对水星和其他行星的最精确的测量是1966年到1990年使用射电望远镜进行的。[註 22]广义相对论对于所有能够精确测量的行星（水星、金星、地球）的轨道进动都预测地非常准确。
  • 根据广义相对论，光在引力场中不沿直线传播，它被大质量物体的引力场弯曲了。星光在经过太阳附近时将被弯曲，星星在夜空中的位置偏折了大约1.75角秒（一角秒是1/3600度）。我们可以在日食时观测离太阳系较近（在天空中的位置，不是实际距离）的恒星来验证这一现象。1919年，一个英国考察队由亚瑟·爱丁顿带领着去了巴西和西非进行观测，验证了爱因斯坦的预测是正确的，而牛顿的理论是错误的。爱丁顿的观测结果并非十分准确，后来用射电天文学的高精度的仪器对遥远的类星体的光线被太阳偏折的观测结果更加精确地证明了爱丁顿的结果（第一次测量是在1967年，最近的一次是2004年）。[註 23]
在这些实验中，只有水星近日点的进动出现在爱因斯坦最终于1916年出版的广义相对论中。后来对他的其他预言的实验验证，尤其是对光线的弯折的测量，使爱因斯坦成名。[註 25]这三个实验使得人们接受了广义相对论，不经意间，很多广义相对论的替代理论出现了。
引力探测器B，太阳能电池板折叠着。
广义相对论的更多的验证包括引力时间延迟效应，最近在2002年由卡西尼号空间探测器测量。一系列实验针对广义相对论对陀螺仪穿越空间时所作的运动的预言。在这些现象中，测地岁差被月球激光测距实验所验证（对月球轨道进行的高精度测量）。另一个关系到旋转的质量的叫做参考系拖拽的预言在2004年被引力探测器B实验，在2008年底得到结果。[註 26]
在宇宙中，太阳系之外的引力是微弱的。因为牛顿的引力定律和爱因斯坦的广义相对论的差别只有在引力很强的时候才能明显地观察到，物理学家一直在一个引力场很强的系统中测试相对论现象。由于对双星的精确观测，我们发现，在这样的恒星系统中，两个致密的中子星互相绕对方旋转。它们之中至少有一个是脉冲星（一个不断辐射出无线电波的天体），就像旋转的灯箱使观察者看到的是闪烁的灯光，这些电波以一定间隔一束一束地到达地球，看上去就像是一系列的脉冲。广义相对论预言了它的电波脉冲和一般的脉冲有区别，例如当电波经过另一个中子星时将受到它的引力场的影响。实际观察到的脉冲信号与广义相对论的预言非常接近</ref> Kramer（2004年）</ref>。
个别项目的观测结果在实际应用中有着突出的贡献，比如需要精确定位和计时的卫星导航系统：全球定位系统。这样的系统中需要两套原子钟：一套放在绕地球旋转的卫星上，一套在地球上。广义相对论预言这两套钟的时间流逝速度是不一样的，取决于它们不同的运动状态（狭义相对论的预言）和它们在地球引力场中的位置。为了保证系统的准确，防止相对论现象造成的两套系统的时间不一致，使用了一个模拟算法来调整钟的时间。系统准确性的试验，尤其是UTC的定义中的非常完整的测量方法，都是对相对论的预言的验证。[註 27]
大量的其他测试都表明了不同版本的等效原理的正确性：严格地讲，所有对引力时间膨胀的测量都验证了弱等效原理，而不是广义相对论本身。到目前为止，广义相对论通过了所有可观测的测试。[註 28]

在天体物理学中的应用[编辑]

基于广义相对论的模型在天体物理学中扮演着重要的角色，这些模型的成功也更加证明了广义相对论的正确性。

引力透镜[编辑]

爱因斯坦十字: 由引力透镜而产生的四个相同天体的图像
因为光在引力场中向下偏转，一个遥远物体的光线可能会有2个或者更多个路线到达地球。比如，类星体的光线可以通过引力透镜星系（lensing galaxy）的一边，然后到达地球上的观察者，或者通过引力透镜星系的另一边到达地球上的同一个观察者。所以，那个观察者将在天空中的两个位置看到同一个天体。这种聚焦现象在透镜中很常见，因此由引力引起的类似现象就叫做引力透镜。[註 29]
观测天文学使用引力透镜现象来研究使引力透镜现象发生的天体的性质，甚至当那个物体不能被直接观察到时，引力透镜现象导致的光线弯曲程度能够帮助我们推断那个天体的质量。引力透镜现象还提供了一个寻找暗物质的方法，暗物质无法被观测到，我们只能通过它造成的引力现象推断它的存在。当产生透镜作用的物质集中在可观测宇宙的重要部分时，我们可以通过它获得关于宇宙的大量信息和它的演化过程。[註 30]

引力波[编辑]

Ambox outdated serious.svg
当前條目或章節需要更新。
請更新本文以反映近況和新增内容。完成修改時，請移除本模板。
引力波是广义相对论的直接推论，它们在时空中以光速传播。（不要与流体动力学中的重力波混淆）
引力波的现象在对一些双星的观测中被间接地探测到。在双星中，两个恒星互相绕着旋转，但它们旋转时，会因为引力波而损失能量。对于像我们的太阳这样的单星来说，这种能量损失太小了而不足以探测到。在1974年，引力波的现象在对叫做PSR B1913+16的双星的观测中探测到了。在这样的一个双星系统中，其中一个是一个脉冲星。脉冲星是非常致密的中子星，对它们而言引力波产生的现象要比单星大的多。同时，脉冲星还会从它的磁极辐射出电磁波。当脉冲星旋转时，它们辐射出的电磁波会经过地球，并以有规则的脉冲的形式被观测到，就像在航海中的船上观测来自灯塔上旋转着的灯，看上去就像是在闪烁。这种脉冲就像是高度准确的时钟，它可以用来衡量双星的旋转周期，并且它对邻近天体造成的时空扭曲反应十分灵敏。
PSR B1913+16的发现者，拉塞尔·赫尔斯和约瑟夫·泰勒，获得了1993年的诺贝尔奖。从那以后，又发现了几个其他的双星。其中最有用的是那些两个恒星都是脉冲星的，因为它们提供了对广义相对论的最精确的测试。[註 31]
现在，对广义相对论主要研究目标就是找到引力波的直接证据。为此，大量地面的引力波探测器正在工作。而空间引力波探测器LISA也正在建造中，首先要完成的任务——LISA航向指示器将在2009年底升空。如果引力波被直接探测到了，它可以被用来获取一些高密度天体的信息，比如中子星和黑洞，也可以用来探测大爆炸后1秒以内的早期宇宙的状态。[註 32]
在M87星系中心区域由黑洞造成的喷流

黑洞[编辑]

广义相对论预言：当物质的质量集中在一个足够小的空间里，将会产生一个引力太过于强大以至于连光都无法逃逸的天体，叫做黑洞。一些类型的黑洞是大质量恒星演化的最终状态。另外，质量达到上千万或者几十亿倍太阳质量的超大质量黑洞被认为是大多数星系的核心，它们在现在关于过去几十亿年间星系的形成过程的理论模型中扮演了重要的角色。[註 33]
物质掉落向高密度的物体会以辐射的形式释放出大量能量，物质落入黑洞可能造成了宇宙中我们能够想象到的最耀眼的现象。天文学家非常感兴趣的例子是类星体和其他形式的活动星系核。掉落向黑洞的物体在黑洞周围吸积可以造成喷流，其中物质以接近光速的速度喷射出来。[註 34]
黑洞的一些性质使得它最有希望帮助科学家找到引力波。其中一个原因是黑洞是双星系统中可能存在的最致密的天体，由这样的系统造成的引力波特别强。另一个原因来自黑洞的无毛定理：随着时间的流逝，黑洞的性质始终只由最少的物理量决定（因为不同人不同的发型使他们有不同的外表，所以这个定理叫做无毛定理）。比如，一个假想的立方体形状的物质的坍缩不会形成一个立方体的黑洞，事实上，它所形成的黑洞和球形物体形成的黑洞没有明显差别，但是仍然有一个很重要的区别：在立方体形状的物质变成球形时将释放出引力波。[註 35]

宇宙学[编辑]

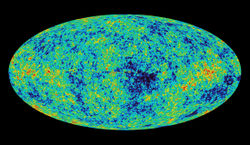
大爆炸后几百万年发出的辐射，由威尔金森微波各向异性探测器摄制
广义相对论的一个重要的观点是：它对于整个宇宙都有效。关键在于，在大尺度下，我们的宇宙的构造似乎非常简单：目前所有的观测表明，平均而言，宇宙的每一个部分都几乎是一样的，无论观察者的位置和观测方向如何，宇宙都近似均匀性和各向同性。像这样比较简单的宇宙可以被爱因斯坦场方程的非常简单的解来解释。现在的宇宙模型是通过结合广义相对论和描述宇宙的物质总体的属性的热力学、原子核物理学以及粒子物理学。根据这些模型，我们现在的宇宙产生于大约140亿年前的一种非常致密、温度非常高的状态（见大爆炸），并且从那以后开始了膨胀。[註 36]
爱因斯坦的场方程可以通过增加一个宇宙常数来一般化。当宇宙常数存在时，真空本身具有相互吸引或者更不寻常的相互排斥的引力。爱因斯坦最初在他1917年关于宇宙学的论文中因为一个特定的目的提到这个方法：当时的宇宙学观点认为宇宙是静态的，在广义相对论的框架内，必须增加一个宇宙常数才能构建一个静态的宇宙。当知道了宇宙不是静态的而是在膨胀，爱因斯坦马上在相对论中去掉了宇宙常数；但是，据我们目前所知道的：从1998年到现在，越来越多的天文观测证据表明，宇宙正在加速膨胀，这就意味着宇宙常数确实存在，或者，与之等价的，有着特定属性的暗能量充满了整个空间。[註 37]

现代的研究[编辑]

广义相对论成功地为一些物理模型提供了一个框架，这些模型解释了很多令人印象深刻的现象。不过，现在仍然有很多悬而未决的有趣问题，在一些情况下，这整个理论几乎一定是不完整的。[註 38]
与其它描述基本相互作用的现代理论相比，广义相对论是一个经典理论：它没有包括量子物理的现象。对于量子化的广义相对论的研究是现代物理学最基本的未解决的问题。现在虽然有一些量子引力理论的候选者，比如弦理论和圈量子引力论，但到目前还没有一个完整的理论出现。人们一直希望量子引力理论能够解决广义相对论的另一个问题：时空中存在引力奇点。这些奇点是时空的边界，在奇点处的几何是定义不明确的，使得广义相对论在这里失效。另外，现在有一个彭罗斯-霍金奇点理论的理论预言如果广义相对论不进行任何量子化，那么这样的奇点一定存在。最有名的例子是宇宙模型中黑洞和宇宙开端的奇点。[註 39]
在宇宙学中，曾经尝试过去修改广义相对论。在现代的宇宙模型中，宇宙中大部分的能量以一种还没有被发现的形式存在，叫做暗能量和暗物质。有一些有争议的观点认为应该通过修改描述宇宙膨胀引力和动力学定律来除去这些神秘的暗物质和暗能量，比如Modified Newtonian dynamics（英文）。[註 40]
在先驱者10号和先驱者11号空间探测器的先驱者异常现象被发现之后，就有了另一个修改爱因斯坦的理论的理由。考虑了所有已知的现象之后，就应该可以准确预言探测器的轨道，但是观测显示理论的预言和探测器的实际位置之间有这微小的差别。虽然正在寻找一个更加传统的解释，又一次物理学革命的可能性仍然没有被排除。[3]
越过了量子现象和宇宙学的挑战之后，对广义相对论的研究就又有可能有进一步的发现：科学家将探索奇点的本质和爱因斯坦场方程的基本性质[4]，甚至对于特定的时空的计算机模拟也将诞生。（比如正在合并的黑洞）[註 41]而对于首先直接探测到引力波的竞赛也在紧张得进行着。[註 42] 在广义相对论诞生的九十多年后，相关的研究比以往更活跃了。[註 43]

注释[编辑]

  1. ^ 这些理论的发展记录在 Renn（2005年），p. 110ff.， Pais（1982年）第9到15章，以及 Janssen（2005年）。 牛顿引力理论的大意可以在 Schutz（2003年），chapters 2–4。我们无法知道爱因斯坦在1907年之前是否想到牛顿的引力理论和狭义相对论的问题，但是根据他自己的说法，他第一次尝试结合牛顿引力理论和狭义相对论是在那一年。 Pais（1982年），p. 178
  2. ^ 这在 Wheeler（1990年）第二章详细描述。
  3. ^ 等效原理在现在对广义相对论的解释中仍然很重要，但是现代的版本跟爱因斯坦的原始版本有些不同。 Norton（1985年）
  4. ^ 例如， Janssen（2005年），p. 64f。爱因斯坦自己也说这在他的非技术书籍《Einstein 1961》中有解释。沿着恩斯特·馬赫的早期想法，爱因斯坦还解释了惯性力和它对应的引力， Stachel（1989年）
  5. ^ 爱因斯坦的计算在 Pais（1982年）的第11b章发表，使用了等效原理，以及狭义相对论关于光的传播和加速的观察者的结果 (考虑每一刻的惯性参考系与加速的观察者一起加速。
  6. ^ 这个现象可以通过狭义相对论计算出，也可以多普勒效应中直接得到。两个理论所的适用范围都是惯性参考系。简单的解释见 Harrison（2002年）
  7. ^ Cf. Ehlers & Rindler（1997年）；非技术性的描述见 Pössel（2007年）。
  8. ^ 这些现象在 Wheeler（1990年），第83–91頁中有詳細的描述。
  9. ^ 潮汐和它们的几何解释请见 Wheeler（1990年）第五章，这部分研究请见 Pais（1982年），第12b章.
  10. ^ 关于时空中的基本对象的介绍，见 Thorne（1994年）第二章第一节以及 Greene（2004年），p. 47–61。更完整的介绍见 Mermin（2005年）、 Wheeler（1990年），第八、九章。
  11. ^ 对于弯曲时空的实证见 Wheeler（1990年），第八、九章 。
  12. ^ 爱因斯坦的发现场方程的奋斗过程见 Pais（1982年）13到15章。
  13. ^ E.g. p. xi in Wheeler（1990年）.
  14. ^ 如果想知道广义相对论中的几何的完整的并且容易理解的介绍和它的应用，参见 Geroch（1978年）。
  15. ^ 见 Wheeler（1990年）第十章。
  16. ^ 事实上，从这个完整的理论开始，爱因斯坦的方程已经可以通过几何来描述这些更加复杂的运动定律 。但是，从理想化的测试粒子得到这些结果是非常复杂的，见 Poisson（2004年）。
  17. ^ 关于质能等价的一个简单解释在 Giulini（2005年）的3.8、3.9节。
  18. ^ 见 Wheeler（1990年）第六章.
  19. ^ 对于度量张量的更详细但更不正规的定义见 Penrose（2004年）14章4节。
  20. ^ 爱因斯坦场方程的几何意义见 Wheeler（1990年）第七第八章；cf. box 2.6 in Thorne（1994年）。一个只需要非常简单的数学的介绍见 Schutz（2003年）第十九章。
  21. ^ 爱因斯坦场方程最重要的解列举在每一本广义相对论的教科书上；在我们现在的理解能力基础上的技术性小结见 Friedrich（2005年）。
  22. ^ 更加准确地说，这些是行星位置的VLBI测量，见 Will（1993年）第五章 Will（2006年）的Section 3.5
  23. ^ 对于历史上的多次测量，见 Hartl（2005年）、 Kennefick（2005年）和 Kennefick（2007年）；Soldner's original derivation in the framework of Newton's theory is Soldner（1804年）. 目前最准确的测量见 Bertotti（2005年）。
  24. ^ 见 Kennefick（2005年）和 Will（1993年）第三章。对天狼星B的测量见 Trimble & Barstow（2007年）。
  25. ^ Pais（1982年）, 水星的近日点进动见pp. 253–254, 爱因斯坦的成名见sections 16b and 16c.
  26. ^ 卡西尼号关于引力时间延迟效应的测量见see Bertotti（2005年）。更多关于引力探测器B的信息见 Gravity Probe B website [2007-06-13] 
  27. ^ 全球定位系统中的相对论现象见 Ashby（2002年），更详细的见 Ashby（2003年）。
  28. ^ 对这些测试的介绍见 Will（1993年）；更加技术性的、前沿的见 Will（2006年）。
  29. ^ 这种情况的几何解释在 Schutz（2003年）第23章中说明。
  30. ^ 对于引力透镜的介绍和它的应用可以在 Newbury（1997年）和 Lochner（2007年）网页上找到。
  31. ^ Schutz（2003年），pp. 317–321; Bartusiak（2000年），pp. 70–86.
  32. ^ 目前正在进行的对引力波的研究见 Bartusiak（2000年）和 Blair & McNamara（1997年）。
  33. ^ 对于从二十世纪初黑洞物理学诞生到现在的发展历史的易懂的概述，见 Thorne（1994年）。对于当今关于黑洞在星系结构的形成过程中的重要角色见 Springel等作者（2005年）；相关的小结见 Gnedin（2005年）。
  34. ^ 见 Sparke & Gallagher（2007年）第8章和 Disney（1998年）。更完整并且只需要简单数学的解释见 Robson（1996年）。
  35. ^ 对黑洞无毛定理的基本介绍见 Chrusciel（2006年）和 Thorne（1994年），pp. 272–286.
  36. ^ 更加详细的信息见 Wright（2007年）中Ned Wright Wright（2007年）的宇宙学教程和FAQ；一个易懂的介绍见 Hogan（1999年）。 Berry（1989年）使用了初等数学但是避免了广义相对论中的高等数学工具，提供了一个更加完整的解释。
  37. ^ 爱因斯坦的原始论文在 Einstein（1917年）；对更多现代的研究介绍见 Cowen（2001年）和 Caldwell（2004年）。
  38. ^ Cf. Maddox（1998年），pp. 52–59 and 98–122; Penrose（2004年），section 34.1 and chapter 30.
  39. ^ 关于弦理论，以及对于量子引力的研究见 Greene（1999年）；对于圈量子引力论的观点，见 Smolin（2001年）.
  40. ^ 对于暗物质，见 Milgrom（2002年）；对于暗能量，见 Caldwell（2004年）.
  41. ^ 要回顾技术的发展和遇到的问题，并展望未来，见 Lehner（2002年）。
  42. ^ 最新的新闻可以在主要探测器的网站，比如GEO 600和LIGO。
  43. ^ 要简要了解对于相对论的现在的研究的，见Living Reviews in Relativity.

参考文献[编辑]

引用[编辑]

  1. ^ 第31届国际中学生奥林匹克物理竞赛，第3题，2009年8月8日查阅。
  2. ^ Mermin（2005年）第12章。
  3. ^ Nieto（2006年）
  4. ^ Friedrich（2005年）

书目[编辑]

外部链接[编辑]

Wikibooks-logo.svg
您可以在維基教科書中查找此百科条目的相關電子教程：

参见[编辑]



隐藏▲
入門、數學表述、验证
基礎概念
现象
方程
進階理論
方程解答
科學家

来自“http://zh.wikipedia.org/w/index.php?title=廣義相對論入門&oldid=26465293”
查看条目评分
给本文评分
这是什么？
可信度
客观性
完整性
可读性
我们将向您发送确认电子邮件。基于反馈隐私政策，我们不会与任何人共享您的地址。
保存成功
你的评分尚未提交
你的评分已过期
请重新评估本条目并重新评分。
发生了一个错误。请稍后重试。
谢谢！你的评分已保存。
您要创建帐户吗？
帐户将帮助您跟踪您所做的编辑，参与讨论，并成为社群的一分子。
或者
谢谢！你的评分已保存。
您知道您可以编辑这个页面吗？