gr01 度量张量是定义在曲面（或者空间、时空）上的所有点上的函数，并将坐标的差别于距离的差别联系起来。所有其他的和几何相关的量，比如曲线的长度，或者两条曲线相交的角度都能够通过度量张量计算出来。

度量张量是定义在曲面（或者空间、时空）上的所有点上的函数，并将坐标的差别于距离的差别联系起来。所有其他的和几何相关的量，比如曲线的长度，或者两条曲线相交的角度都能够通过度量张量计算出来。

https://zh.wikipedia.org/wiki/%E5%BB%A3%E7%BE%A9%E7%9B%B8%E5%B0%8D%E8%AB%96%E5%85%A5%E9%96%80

爱因斯坦场方程[编辑]

爱因斯坦场方程是广义相对论的核心，它使用数学语言精确地描述了物质的性质和时空之间的联系。更具体地，它使用了黎曼几何中的概念和方法。在黎曼几何中，空间（或者时空）的几何性质被一个叫做度量张量的量描述。度量张量将需要的信息组织起来，并计算出弯曲的空间（或者时空）中角和距离的基本的几何概念。

不同纬度上相隔30度的经线之间的距离。

一个简单的例子是像地球表面这样的球面，球面上的任何一点可以表示成两个坐标：地理学的经度和纬度。不像平面上的笛卡尔坐标系，两点之间的距离不仅和它们坐标的差有关，还和它们的位置有关，就像右图：在赤道处（品红色线段）的人向西移动30经度经过的路程大约是3300千米，但是在纬度是55度的地方（蓝色线段）的人向西移动30经度经过的距离大约是1900千米。坐标不能提供足够的信息来描述球面上，或者说是任何更加复杂的空间和时空的几何。这些信息正是度量张量所提供的。度量张量是定义在曲面（或者空间、时空）上的所有点上的函数，并将坐标的差别于距离的差别联系起来。所有其他的和几何相关的量，比如曲线的长度，或者两条曲线相交的角度都能够通过度量张量计算出来。^{[註 19]}

度量张量函数和它的变化率可以用来定义另一个几何量：黎曼曲率张量，它描述了空间（或者时空）在每一点处如何弯曲。在广义相对论中，度量张量和黎曼曲率张量是定义在时空的每一点上的量。就像我们已经提到的，时空中的物质定义了另一个量：能量-动量张量T，“时空告诉物质如何运动，物质告诉时空如何弯曲”的原理意味着这些量必须互相联系。爱因斯坦通过用黎曼曲率张量和度量张量来定义另一个量G来表示这种联系，这个量G现在被叫做爱因斯坦张量，它描述了时空弯曲的方式。于是，爱因斯坦场方程可以表示成：
通过几个常量，G（描述曲率）可以换算成T（描述物质的含量）。在这个方程中的常数反应了不同的理论的结合：G是在牛顿的引力理论中就已经出现的引力常数；c是光速，狭义相对论的关键；π是圆周率，最基本的几何常数之一。
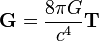
方程中的G和T 又各自被几个关于时空中的坐标的函数决定，而这个方程与这些函数是等同的。^{[註 20]}这些方程的一个解描述了一个特定的时空，例如，史瓦西解描述了像恒星和黑洞等球形的不旋转的大质量物体附近的时空，克尔解描述了旋转的黑洞。还有其他的解能够描述引力波，弗里德曼-勒梅特-罗伯逊-沃尔克解描述了膨胀的宇宙。最简单的解是狭义相对论中平直的闵可夫斯基时空。^{[註 21]}