前两项是经典力学的结果:第一项是牛顿引力势能(负值表示吸引),第二项是具有排斥效应的离心势能;而第三项仅在广义相对论中存在,它代表的是一个与距离立方成反比的吸引势能。从后文或其他文献中可以看到,这种立方反比势能造成了粒子运动周期中椭圆轨道的逐渐相对论进动
一个质量为
 的粒子在一个一维势阱中运动
的粒子在一个一维势阱中运动拉普拉斯-龍格-冷次向量- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/拉普拉斯-龍格-冷次向量
广义相对论中的开普勒问题- 维基百科,自由的百科全书
https://zh.wikipedia.org/zh-hk/广义相对论中的开普勒问题
广义相对论中的开普勒问题[编辑]
维基百科,自由的百科全书
 和另一个物体的质量
和另一个物体的质量 相比可忽略,这种近似对应着实际情形中地球绕太阳公转,以及一个光子在一颗恒星的引力场中的运动等问题。在这些情形下,可以认为大质量
相比可忽略,这种近似对应着实际情形中地球绕太阳公转,以及一个光子在一颗恒星的引力场中的运动等问题。在这些情形下,可以认为大质量 的位置在空间中是固定的,并且只有大质量的引力场对周围时空曲率变化有贡献。这时的时空曲率可由爱因斯坦场方程的史瓦西解来描述;而小质量
的位置在空间中是固定的,并且只有大质量的引力场对周围时空曲率变化有贡献。这时的时空曲率可由爱因斯坦场方程的史瓦西解来描述;而小质量 (以下简称“粒子”)的运动可由史瓦西解的测地线方程来描述。由于假设小质量
(以下简称“粒子”)的运动可由史瓦西解的测地线方程来描述。由于假设小质量 是点状的无尺寸粒子,两者之间的潮汐力可忽略。
是点状的无尺寸粒子,两者之间的潮汐力可忽略。从测地线方程可以推出广义相对论的关键性实验证据,著名的水星近日点的进动,以及光线在太阳引力场中的偏折。对于前者,广义相对论为观测到的这一现象提供了漂亮的解释,而后者则是广义相对论的著名预言,其正确性被亚瑟·爱丁顿爵士的实验观测所证实。
广义相对论的两体问题中还涉及了引力辐射造成的轨道衰减,这是一个纯粹的相对论效应,没有对应的经典力学版本。这个问题并不包含在史瓦西解中,请参见引力辐射和引力波天文学。
目录[隐藏] |
历史背景-爱因斯坦的直觉[编辑]

没有其他外力存在时,一个粒子在牛顿有心力的作用下绕着另一个粒子公转的轨道永远是一个不变的椭圆稳定轨道。当有其他外力存在(例如来自其他行星的引力)时,这样的轨道会逐渐发生转动,这种转动(被称作轨道进动)的速率可以被测量得非常精确。如果知道了这些外力的大小和方向,通过牛顿力学也可以对这种轨道进动的速率进行理论预测。不过在1859年对水星轨道进动的观测中,牛顿力学没有给出和实验观察相一致的预言。
1905年,爱因斯坦提出了狭义相对论,这一理论否决了任何超过光速传播的效应的可能性;不过同时,这也暗示了相对论的基本假设和牛顿天体力学的矛盾。拉普拉斯早先在其研究中证明,如果引力相互作用不是超距的(即传播是瞬时的),行星的运动将不再严格满足动量守恒定律(类似于电磁相互作用中一部分动量要传递给电磁相互作用的媒介子,引力相互作用中也需要携带动量的媒介子)。从牛顿力学的观点来看,如果引力相互作用只能以有限速度传播,那么在任意时刻,行星受到的来自太阳的引力将不会指向太阳所在的即时位置,而是在若干时间之前的位置。在经典力学的基础上,拉普拉斯推导出当引力以光速传播时太阳系是不稳定的,并只能维持并不太长时间的存在。而对太阳系的实际观测表明,如果引力的传播速度确实存在一个上限,根据经典力学这个上限将比光速高出好几个数量级。
这种矛盾引出了建立一个替代牛顿引力理论的新理论的需求,这个新理论需要满足狭义相对论的基本假设,并且在相对论效应可忽略时能够和牛顿的引力理论相容。1907年爱因斯坦确认了建立一个狭义相对论的后继理论的必要性,这个理论能够同时包含狭义相对论的基本假设和万有引力相互作用。在1907年至1915年间,爱因斯坦在等效原理的基础上逐渐发展了他的新理论。根据等效原理,一个均一的引力场对在其内所有物体的作用都是相同的,因此这个引力场将不能被一个处于自由落体状态的观察者观测到。归纳而言,所有局部的引力效应都可以在一个直线加速的非惯性参考系中体现出来,这个原理反过来也成立,即加速参考系等效于一个局部的引力场。这样看来,引力和离心力以及科里奥利力等惯性力这样的“虚力”有相类似的效应:惯性力都来源于一个加速的非惯性系,并且和物体的惯性质量成正比,引力亦然(由于惯性质量和引力质量等价)。想要在等效原理的基础上将万有引力和狭义相对论的基本假设统一起来,需要牺牲的是经典力学中习以为常的基本假设:我们所处的时空是一个符合欧几里得几何的平直时空。爱因斯坦使用的是一种更一般的几何学:黎曼几何,在黎曼几何描述下的时空可以是弯曲的。经过八年的研究,他成功得到了一个能够包含引力理论的更一般的相对论性理论:广义相对论。广义相对论要求时空是弯曲的,这种时空的弯曲性是引力的体现,也是一种物理上的实在,这和惯性力不过是假想的“虚力”完全不同。广义相对论首先成功解释了水星近日点的进动误差并预言了光线在太阳引力场中的偏折,这个预言在广义相对论发表之后得到了实验证实。
几何基础-度规[编辑]
在经典的欧几里得几何中,三角形满足勾股定理(毕达哥拉斯定理),这意味着空间中两点间的距离平方等于空间中所有完备正交分量平方和: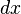 、
、 、
、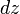 表示在笛卡尔坐标系下三个坐标轴
表示在笛卡尔坐标系下三个坐标轴 、
、 、
、 上各自两点间的无穷小距离。
上各自两点间的无穷小距离。现在想象存在一个笛卡尔坐标不适用的世界,其间两点的距离由下式描述:
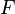 、
、 、
、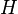 是坐标
是坐标 、
、 、
、 的任意函数。想象一个这样的世界其实并不困难,我们就生活在这样一个表面是弯曲的世界上,这也是无法精确描绘出一个平面的世界地图的原因。想要简明地描述这个世界的表面几何不适合采用笛卡尔坐标,比较简单的做法是球坐标系
的任意函数。想象一个这样的世界其实并不困难,我们就生活在这样一个表面是弯曲的世界上,这也是无法精确描绘出一个平面的世界地图的原因。想要简明地描述这个世界的表面几何不适合采用笛卡尔坐标,比较简单的做法是球坐标系 ,这时的欧几里得几何中的距离表示为:
,这时的欧几里得几何中的距离表示为: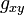 等构成了空间的度规张量,它定义了黎曼几何框架下的空间几何。在球坐标系下交叉项不存在,它只包含有三个非零的张量元素:
等构成了空间的度规张量,它定义了黎曼几何框架下的空间几何。在球坐标系下交叉项不存在,它只包含有三个非零的张量元素:在狭义相对论中,爱因斯坦就已经指出空间中两点的距离并不是恒量,而与观察者的运动(即惯性参考系)有关。狭义相对论指出在任何惯性系下观测到的恒量是两点间的时空间隔,这个间隔被称作固有时。固有时是一个相对论不变量,它与惯性参考系无关。
 取决于时空中发出引力的质量、动量和能量,描述这一关系的是爱因斯坦的引力场方程。爱因斯坦的引力理论不仅和当时已知的物理定律相容,它还成功预言了很多从未观测到的物理现象,这些现象至今仍然不断被实验观测所证实。
取决于时空中发出引力的质量、动量和能量,描述这一关系的是爱因斯坦的引力场方程。爱因斯坦的引力理论不仅和当时已知的物理定律相容,它还成功预言了很多从未观测到的物理现象,这些现象至今仍然不断被实验观测所证实。史瓦西几何[编辑]
爱因斯坦场方程的解的最简单形式是史瓦西度规,它对应着一个不带电荷和角动量的球对称的质量 的引力场,其形式为:
的引力场,其形式为: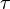 是固有时;
是固有时;  是光速;
是光速;  是时间坐标;
是时间坐标;  是球面的径向坐标;
是球面的径向坐标;  是球面的纬度坐标;
是球面的纬度坐标;  是球面的经度坐标;
是球面的经度坐标;  是中心质量
是中心质量 的史瓦西半径,其关系为
的史瓦西半径,其关系为测地线方程[编辑]
根据广义相对论,质量可忽略的粒子在引力场中沿着测地线运动。在无引力的平直时空中,测地线是直线;但当时空存在弯曲时,测地线由下面的测地线方程描述[3]: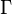 是克里斯托费尔符号而变量
是克里斯托费尔符号而变量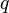 是一个将粒子在时空中的轨迹即世界线参数化的参量。克里斯托费尔符号只和度规对坐标的一阶偏导数有关(即描述了度规如何随坐标变化)。对于类时的轨迹(有质量的粒子,速度小于光速)而言,参数
是一个将粒子在时空中的轨迹即世界线参数化的参量。克里斯托费尔符号只和度规对坐标的一阶偏导数有关(即描述了度规如何随坐标变化)。对于类时的轨迹(有质量的粒子,速度小于光速)而言,参数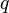 一般取作固有时;而对于类光的轨迹(无质量的粒子,速度为光速)固有时为零,因此严格来讲不能将固有时用作参数;不过类光可以看作是类时的极端相对论情形,有时从而可以通过取极限的方法,从类时的轨迹导出粒子质量为零时类光的轨迹,并保持总能量不变。
一般取作固有时;而对于类光的轨迹(无质量的粒子,速度为光速)固有时为零,因此严格来讲不能将固有时用作参数;不过类光可以看作是类时的极端相对论情形,有时从而可以通过取极限的方法,从类时的轨迹导出粒子质量为零时类光的轨迹,并保持总能量不变。在度规具有对称性的场合下我们往往可以将问题简化。例如史瓦西度规是关于平面
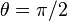 对称的,任何起始于这一平面上测地线的粒子将保持在这一平面上运动。因此我们总可以认为粒子的轨道保持在这一平面上,即纬度坐标
对称的,任何起始于这一平面上测地线的粒子将保持在这一平面上运动。因此我们总可以认为粒子的轨道保持在这一平面上,即纬度坐标 恒等于
恒等于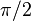 ,这时的史瓦西度规简化为
,这时的史瓦西度规简化为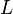 的定义,得到如下替换关系可消去式中的固有时
的定义,得到如下替换关系可消去式中的固有时 、
、 的定义为
的定义为光线在太阳引力场中偏折的近似公式[编辑]
 趋于无穷大)时,轨道方程的解变为如下形式:
趋于无穷大)时,轨道方程的解变为如下形式: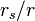 的幂指数展开,得到的领导项给出了一个来自无穷远处的无质量粒子在史瓦西引力场中的运动角度近似偏移量(其后这个粒子仍然向无穷远处运动)
的幂指数展开,得到的领导项给出了一个来自无穷远处的无质量粒子在史瓦西引力场中的运动角度近似偏移量(其后这个粒子仍然向无穷远处运动) 可理解为粒子在运动过程中距中心质量的最近距离。尽管这个公式是通过相当的近似得到的,在大多数有关引力透镜的测量中它都相当精确,这是因为对大多数星体而言
可理解为粒子在运动过程中距中心质量的最近距离。尽管这个公式是通过相当的近似得到的,在大多数有关引力透镜的测量中它都相当精确,这是因为对大多数星体而言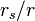 都很小。对于掠过太阳表面的光子,其角偏移量大约只有1.75角秒。
都很小。对于掠过太阳表面的光子,其角偏移量大约只有1.75角秒。和经典力学的关系[编辑]
从上面得到的史瓦西度规中的粒子运动方程 的粒子在一个一维势阱中运动,其有效势能为
的粒子在一个一维势阱中运动,其有效势能为 是椭圆的半长轴,
是椭圆的半长轴, 是偏心率。
是偏心率。在
 很小时,由于是立方反比关系第三项起主导作用,这决定了一个关键性的最内稳定圆半径
很小时,由于是立方反比关系第三项起主导作用,这决定了一个关键性的最内稳定圆半径 ,如果粒子一旦处于小于这个半径的范围内,它最终会不可避免地向内坠入。这个最内半径是单位质量的角动量的函数,即上面定义的长度参数
,如果粒子一旦处于小于这个半径的范围内,它最终会不可避免地向内坠入。这个最内半径是单位质量的角动量的函数,即上面定义的长度参数 。
。圆轨道和其稳定性[编辑]
 ,有效势能
,有效势能 可写成如下形式:
可写成如下形式: 和
和
 对应的圆规道是不稳定的,这个原因在上面已经提到:由于当
对应的圆规道是不稳定的,这个原因在上面已经提到:由于当 很小时,立方反比项增长速度远大于其他两项,这个引力将把粒子强烈地吸引到引力场中心处。而靠外的半径
很小时,立方反比项增长速度远大于其他两项,这个引力将把粒子强烈地吸引到引力场中心处。而靠外的半径 对应的圆规道是稳定的,这是因为在那附近立方反比项并不显著,系统基本可近似为一个非相对论的开普勒系统。
对应的圆规道是稳定的,这是因为在那附近立方反比项并不显著,系统基本可近似为一个非相对论的开普勒系统。当长度参数
 远大于史瓦西半径
远大于史瓦西半径 时(经典极限),这两个圆轨道半径公式近似为
时(经典极限),这两个圆轨道半径公式近似为 和
和 的定义代入
的定义代入 ,就得到了粒子围绕中心质量
,就得到了粒子围绕中心质量 公转的有心力问题
公转的有心力问题 是粒子的角速度。这个公式可以直接在经典理论下让惯性离心力等于牛顿万有引力得到
是粒子的角速度。这个公式可以直接在经典理论下让惯性离心力等于牛顿万有引力得到 由上逐渐逼近
由上逐渐逼近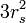 时,这两个圆轨道半径重合为一个值:
时,这两个圆轨道半径重合为一个值: 和
和 的二项式解保证了
的二项式解保证了 总是大于
总是大于 的,而
的,而 总是在
总是在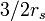 和
和 的范围内。半径小于
的范围内。半径小于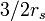 的圆轨道是不能存在的。对于无质量的粒子,长度参数
的圆轨道是不能存在的。对于无质量的粒子,长度参数 为无穷大,例如对于光子可以存在一个
为无穷大,例如对于光子可以存在一个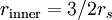 的圆轨道,这个半径所构成的球有时被称作光子球。
的圆轨道,这个半径所构成的球有时被称作光子球。椭圆轨道进动的推导[编辑]
 可以推出轨道的进动速度。首先,圆轨道
可以推出轨道的进动速度。首先,圆轨道 的一个微小的半径变化会造成在
的一个微小的半径变化会造成在 上的稳定的谐振动,其振动的角频率为
上的稳定的谐振动,其振动的角频率为 的形式代入并求二阶导数,
的形式代入并求二阶导数,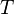 就得到了在一个周期内的轨道进动的角位移
就得到了在一个周期内的轨道进动的角位移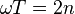 以及长度参数
以及长度参数 的定义。代入史瓦西半径
的定义。代入史瓦西半径 的定义得到
的定义得到 和偏心率
和偏心率 可以简化这个公式,开普勒第三定律在这里可以写为
可以简化这个公式,开普勒第三定律在这里可以写为使用椭圆函数的圆轨道的解[编辑]
轨道方程 、
、 由下式给出
由下式给出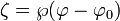 ,这里
,这里 是参数为
是参数为 和
和 的魏尔施特拉斯椭圆函数,
的魏尔施特拉斯椭圆函数, 是一个积分常数(可以是复数)。
是一个积分常数(可以是复数)。可能轨道的定性分析[编辑]
对于轨道方程 大于零,则三次方程
大于零,则三次方程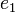 、
、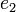 、
、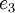 ,将它们按从大到小排列
,将它们按从大到小排列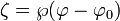 是一个具有两个半周期的椭圆函数,其中一个完全是实的:
是一个具有两个半周期的椭圆函数,其中一个完全是实的: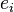 相联系,方程中
相联系,方程中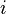 可以等于1、2、3。因此如果
可以等于1、2、3。因此如果 被设置为等于其中任何一个半周期,
被设置为等于其中任何一个半周期,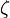 的导数就为零,这对应着一个近星点或远星点:
的导数就为零,这对应着一个近星点或远星点: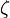 等于根
等于根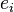 时,导数的值为零。
时,导数的值为零。不同轨道的定性性质取决于
 的选取。
的选取。 等于
等于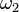 的解对应着在
的解对应着在 和
和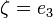 之间周期性变化的轨道,或者是散射到无穷远处的轨道(
之间周期性变化的轨道,或者是散射到无穷远处的轨道( )。而
)。而 等于
等于 或任何其他实数对应着衰减至半径等于零的轨道,这是由于
或任何其他实数对应着衰减至半径等于零的轨道,这是由于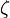 作为一个实数时不能小于
作为一个实数时不能小于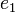 ,结果就不可避免地增长至无穷大。
,结果就不可避免地增长至无穷大。准椭圆轨道[编辑]
在系统能量满足不等式E2 < m2 c4的前提下, 等于
等于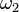 时方程的解
时方程的解 给出了一个实数的
给出了一个实数的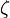 值。对于这类解,变量
值。对于这类解,变量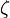 的值被限制在
的值被限制在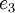 和
和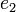 之间。如果这两个根都大于-1/12,
之间。如果这两个根都大于-1/12,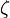 将不会等于-1/12,也就不会产生半径趋于无穷大的散射轨道。因此这类解对应着一个逐渐进动的椭圆轨道,当粒子(或行星)从起始状态开始演化时,其半径在最小半径
将不会等于-1/12,也就不会产生半径趋于无穷大的散射轨道。因此这类解对应着一个逐渐进动的椭圆轨道,当粒子(或行星)从起始状态开始演化时,其半径在最小半径 和最大半径
和最大半径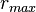 之间振荡,分别为
之间振荡,分别为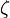 的两个极值。魏尔施特拉斯椭圆函数的实数周期为
的两个极值。魏尔施特拉斯椭圆函数的实数周期为 ,因此当粒子进动了
,因此当粒子进动了 的角位移后将回到与先前相同的半径,椭圆轨道处于进动状态(注意
的角位移后将回到与先前相同的半径,椭圆轨道处于进动状态(注意 一般来说不等于
一般来说不等于 ,但两者的差值即每个轨道周期内进动的角位移很小)。
,但两者的差值即每个轨道周期内进动的角位移很小)。稳定圆轨道[编辑]
这是2e2 = 2e3 = −e1的特殊情形,即方程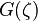 有两个根相等并且是负值,而第三个根是正值。在这种情况下
有两个根相等并且是负值,而第三个根是正值。在这种情况下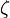 有两个相同的实根e = e2 = e4,这个解对应着经典的圆轨道,即上面得到的半径为
有两个相同的实根e = e2 = e4,这个解对应着经典的圆轨道,即上面得到的半径为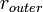 的轨道,并且我们看到
的轨道,并且我们看到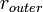 一定大于
一定大于 。这样的圆轨道之所以稳定,是因为对方程参数的一个微扰只会让这两个实根略微不等,从而得到准椭圆轨道解。例如对处于稳定圆轨道上粒子的一个微小扰动会将它推到准椭圆轨道上去并逐渐开始进动。
。这样的圆轨道之所以稳定,是因为对方程参数的一个微扰只会让这两个实根略微不等,从而得到准椭圆轨道解。例如对处于稳定圆轨道上粒子的一个微小扰动会将它推到准椭圆轨道上去并逐渐开始进动。非束缚(散射)轨道[编辑]
轨道半径趋于无穷大对应着粒子飞向无限远处,这时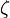 等于-1/12。这样的非束缚轨道对应着两个实根的值分别落在-1/12两侧,即 e2 ≤ −1/12 ≤ ζ ≤ e3。
等于-1/12。这样的非束缚轨道对应着两个实根的值分别落在-1/12两侧,即 e2 ≤ −1/12 ≤ ζ ≤ e3。渐近圆轨道[编辑]
当-e3 = 2e2 = 2e1,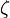 有两个正的且相同的实根,而第三个根e3是负值。将重根代换为
有两个正的且相同的实根,而第三个根e3是负值。将重根代换为 ,在
,在 等于正负无穷时粒子具有渐近的圆轨道:
等于正负无穷时粒子具有渐近的圆轨道: 等于正负无穷时,粒子渐近地接近这个圆轨道:
等于正负无穷时,粒子渐近地接近这个圆轨道: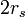 和
和 之间。
之间。渐近的圆轨道也可以通过用雅可比椭圆函数来表示魏尔施特拉斯椭圆函数得到:
 ,并且椭圆积分的模数为
,并且椭圆积分的模数为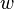 趋于
趋于 。这样选择
。这样选择 的值为
的值为 (四分之一周期)就可以得到上面的渐近圆轨道。
(四分之一周期)就可以得到上面的渐近圆轨道。衰减轨道[编辑]
当 等于
等于 (或其他实数)时,
(或其他实数)时,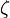 的实根有性质
的实根有性质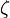 总不小于e1,这使得轨道方程
总不小于e1,这使得轨道方程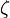 值都是正的,并且
值都是正的,并且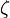 可以无限制增长,这对应着粒子轨道逐渐向
可以无限制增长,这对应着粒子轨道逐渐向 处衰减。
处衰减。对测地线方程解的修正[编辑]
根据广义相对论,两个互相绕转的质量例如双星系统会发出引力辐射,由引力辐射携带的能量会让它们的轨道稍微偏离测地线方程所得到的结果。关于这一问题的最著名间接验证是由拉塞尔·赫尔斯和约瑟夫·泰勒对一个脉冲双星PSR B1913+16的观测,两人因此获得1993年的诺贝尔物理学奖。系统内的两颗中子星距离非常接近,且绕转速度非常之快,测量到的一个周期时长大约仅为465分钟。两颗中子星的轨道是高度椭圆的,偏心率达到0.62。按照广义相对论的预言,这样短的轨道周期和高度的偏心轨道使得这个双星系统成为一个非常好的引力波源,通过引力辐射损失的能量使轨道逐渐衰减,轨道周期逐渐变短。通过长达三十年的实验观测,即使是在可以达到的最精确的测量下轨道周期的降低和广义相对论的预言仍符合得相当好。广义相对论还预言,再过三亿年后这两颗恒星最终会碰撞到一起。开普勒问题中因引力辐射导致的能量和角动量的损耗公式已经通过计算得到[6],在一个完整的轨道周期内取平均下的能量变化率为[7]
轨道方程的理论力学推导[编辑]
哈密顿-雅可比方法[编辑]
开普勒运动的轨道方程也可以通过哈密顿-雅可比方程推导出。这种方法的好处是它可以将一个粒子的运动等价于一束波的传播,这就很容易进而通过费马原理推导出光线在引力场中的偏折公式。这种方法的解释是,由于引力场的延时效应,一束波的波前靠近中心质量 的部分要比远离中心质量的部分运动得慢,这就导致了波前传播方向的改变。
的部分要比远离中心质量的部分运动得慢,这就导致了波前传播方向的改变。使用一般的协变性,一个粒子在任意坐标下的哈密顿-雅可比方程可以表示为
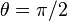 的球坐标系。假设哈密顿主函数
的球坐标系。假设哈密顿主函数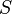 是可分离变量的,则其应具有如下形式:
是可分离变量的,则其应具有如下形式: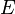 和
和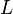 分别是粒子的能量和角动量。从哈密顿-雅可比方程可以得到哈密顿主函数径向分量
分别是粒子的能量和角动量。从哈密顿-雅可比方程可以得到哈密顿主函数径向分量 的积分解:
的积分解:在质量趋于零(或
 趋于无穷大)时,哈密顿主函数简化作下面的形式:
趋于无穷大)时,哈密顿主函数简化作下面的形式:拉格朗日方法[编辑]
在广义相对论中,无质量粒子在时空中的运动轨迹是测地线,这是等效原理的要求。从最小作用量原理的观点来看,测地线长度的变分为零,即: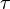 是固有时,
是固有时, 是测地线在时空中的弧长。
是测地线在时空中的弧长。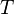 在这里的定义是
在这里的定义是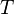 可以写成
可以写成 和
和 应用,可得到两个守恒量:
应用,可得到两个守恒量: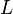 和
和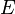 的方程:
的方程:哈密顿原理[编辑]
只受到引力作用的粒子的作用量为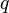 是任意能够将粒子的世界线可微化的参数,对这个作用量使用变分法就可以得到测地线方程。不过如果我们对被积函数的平方求变分过程会更简单,根据度规这个平方的形式为
是任意能够将粒子的世界线可微化的参数,对这个作用量使用变分法就可以得到测地线方程。不过如果我们对被积函数的平方求变分过程会更简单,根据度规这个平方的形式为 取变分可得
取变分可得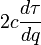 就得到了被积函数的变分:
就得到了被积函数的变分: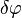 可以任意取值,只有当被积函数的另一部分处处为零时才能保证等式右边为零,因此得到运动方程:
可以任意取值,只有当被积函数的另一部分处处为零时才能保证等式右边为零,因此得到运动方程: 取变分可得
取变分可得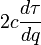 得到被积函数的变分:
得到被积函数的变分:参考文献[编辑]
引用[编辑]
- ^ Le Verrier, UJJ. Unknown title. Comptes Revues d'Academie de la Science de Paris. 1859, 49: 379–?.
- ^ 2.0 2.1 Pais, A. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press. 1982: pp. 253–256. ISBN 0-19-520438-7.
- ^ Weinberg 1972.
- ^ Whittaker 1937.
- ^ Landau and Lifshitz (1975), pp. 306–309.
- ^ Peters PC, Mathews J. Unknown title. Physical Review. 1963, 131: 435–?.
- ^ Landau and Lifshitz, p. 356–357.
- ^ Landau and Lifshitz (1975), pp. 307–308.
书籍[编辑]
- Adler, R; Bazin M, and Schiffer M. Introduction to General Relativity. New York: McGraw-Hill Book Company. 1965: pp. 177–193. ISBN 978-0-07-000420-7.
- Einstein, A. The Meaning of Relativity 5th. ed. Princeton, NJ: Princeton University Press. 1956: pp. 92–97. ISBN 978-0-691-02352-6.
- Lanczos, C. The Variational Principles of Mechanics 4th ed. New York: Dover Publications. : pp. 330–338. ISBN 978-0-486-65067-8.
- Landau, LD; Lifshitz, EM. The Classical Theory of Fields (Course of Theoretical Physics, Vol. 2) revised 4th English ed. New York: Pergamon Press. 1975: pp. 299–309. ISBN 978-0-08-018176-9.
- Misner, CW; Thorne, K, and Wheeler, JA. Gravitation. San Francisco: W. H. Freeman. 1973: Chapter 25 (pp. 636–687), §33.5 (pp. 897–901), and §40.5 (pp. 1110–1116). ISBN 978-0-7167-0344-0.
- Pauli, W. Theory of Relativity translated by G. Field. New York: Dover Publications. 1958: pp. 40–41, 166–169. ISBN 978-0-486-64152-2.
- Rindler, W. Essential Relativity: Special, General, and Cosmological revised 2nd ed. New York: Springer Verlag. 1977: pp. 143–149. ISBN 978-0-387-10090-6.
- Synge, JL. Relativity: The General Theory. Amsterdam: North-Holland Publishing. 1960: pp. 289–298. ISBN 978-0-7204-0066-3.
- Wald, RM. General Relativity. Chicago: The University of Chicago Press. 1984: pp. 136–146. ISBN 978-0-226-87032-8.
- Weinberg, S. Gravitation and Cosmology. New York: John Wiley and Sons. 1972: pp. 185–201. ISBN 978-0-471-92567-5.
- Whittaker, ET. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, with an Introduction to the Problem of Three Bodies 4th ed. New York: Dover Publications. 1937: pp. 389–393. ISBN 978-1-114-28944-4.
期刊文章[编辑]
- Hagihara, Y. Theory of the relativistic trajectories in a gravitational field of Schwarzschild. Japanese Journal of Astronomy and Geophysics. 1931, 8: 67–176. ISSN 0368-346X.
参见[编辑]
| |||||||||||||||||||||||


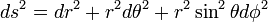

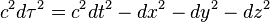



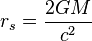
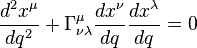
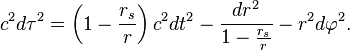
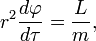
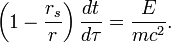

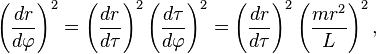



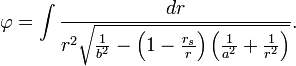

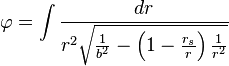
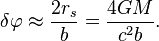
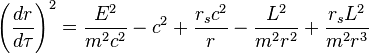
![\frac{1}{2} m \left( \frac{dr}{d\tau} \right)^{2} =
\left[ \frac{E^{2}}{2mc^{2}} - \frac{1}{2} mc^{2} \right]
+ \frac{GMm}{r} - \frac{L^{2}}{2m r^{2}} + \frac{GM L^{2}}{c^{2} m r^{3}}](https://upload.wikimedia.org/math/9/9/8/998f134e80762205885a618eca5b0543.png)



 等于
等于 时,一个处于亚稳态的圆规道是可能的,在图中用绿圈标记。对于更高的角动量,由于离心势能的存在会有不稳定的圆规道出现,在图中用红圈标记。
时,一个处于亚稳态的圆规道是可能的,在图中用绿圈标记。对于更高的角动量,由于离心势能的存在会有不稳定的圆规道出现,在图中用红圈标记。![V(r) = \frac{mc^{2}}{2} \left[ - \frac{r_{s}}{r} + \frac{a^{2}}{r^{2}} - \frac{r_{s} a^{2}}{r^{3}} \right]](https://upload.wikimedia.org/math/0/0/6/0069f6312c1e8648428fc6acdeb8d22c.png)
![F = -\frac{dV}{dr} = -\frac{mc^{2}}{2r^{4}} \left[ r_{s} r^{2} - 2a^{2} r + 3r_{s} a^{2} \right] = 0](https://upload.wikimedia.org/math/8/c/1/8c1a8419a45cbed79799280b0bb1ff35.png)
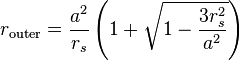

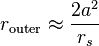
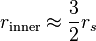



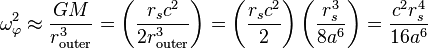
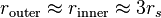

![\omega_{r}^{2} = \frac{1}{m} \left[ \frac{d^{2}V}{dr^{2}} \right]_{r=r_{\mathrm{outer}}}](https://upload.wikimedia.org/math/6/f/f/6ffa699f239d2cf49c8cf9691cc1d9aa.png)
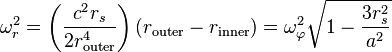
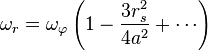


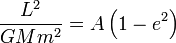

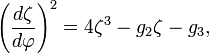
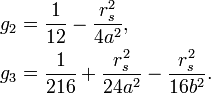


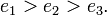

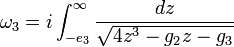
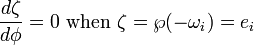
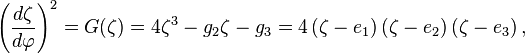
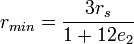
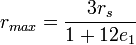
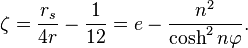


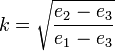
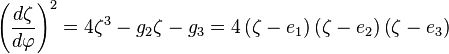

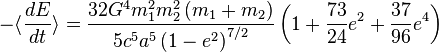
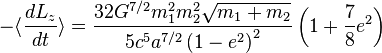


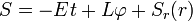
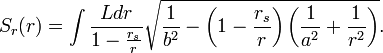
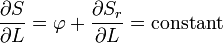

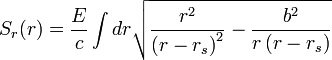
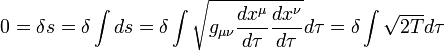
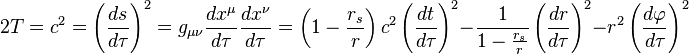
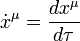

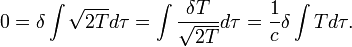

![\frac{d}{d\tau} \left[ r^{2} \frac{d\varphi}{d\tau} \right] = 0,](https://upload.wikimedia.org/math/b/d/b/bdb34bc8975d6a2db57c920ea817aa7a.png)
![\frac{d}{d\tau} \left[ \left( 1 - \frac{r_{s}}{r} \right) \frac{dt}{d\tau} \right] = 0,](https://upload.wikimedia.org/math/d/a/4/da4c33d90493039313734fe1da39a88e.png)
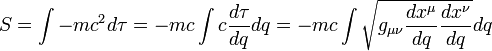
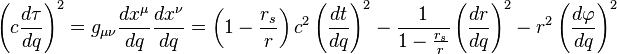
![\delta \left(c \frac{d\tau}{dq}\right)^2 = 2 c^{2} \frac{d\tau}{dq} \delta \frac{d\tau}{dq} =
\delta \left[ \left( 1 - \frac{r_{s}}{r} \right) c^{2} \left( \frac{dt}{dq} \right)^{2} -
\frac{1}{1 - \frac{r_{s}}{r}} \left( \frac{dr}{dq} \right)^{2} -
r^{2} \left( \frac{d\varphi}{dq} \right)^{2} \right]](https://upload.wikimedia.org/math/f/c/3/fc310a1d30f2a716203953702c1eb9e0.png)
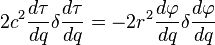


![0 = - \frac{r^{2}}{c} \frac{d\varphi}{d\tau} \delta \varphi
- \int { \frac{d}{dq} \left[ - \frac{r^{2}}{c} \frac{d\varphi}{d\tau} \right] \delta \varphi dq }](https://upload.wikimedia.org/math/6/f/5/6f5b2e6689c3d482ee5e6e172da6904a.png)
![\frac{d}{dq} \left[ - \frac{r^{2}}{c} \frac{d\varphi}{d\tau} \right] = 0](https://upload.wikimedia.org/math/1/6/e/16ed97b28f7f3aac3a4b7928feed41f8.png)



![0 = c \left( 1 - \frac{r_{s}}{r} \right) \frac{dt}{d\tau} \delta t
- \int { \frac{d}{dq} \left[ c \left( 1 - \frac{r_{s}}{r} \right) \frac{dt}{d\tau} \right] \delta t dq }](https://upload.wikimedia.org/math/3/8/0/380a7401b4f0f6a0866229274066db50.png)
![\frac{d}{dq} \left[ c \left( 1 - \frac{r_{s}}{r} \right) \frac{dt}{d\tau} \right] = 0](https://upload.wikimedia.org/math/6/0/7/607e6cdc0463ec57670ae0ec66deb220.png)

No comments:
Post a Comment