
Mathephysician
This is a field of Mathematics and Physics.Just for fun.But the beauty of God will be seen by us.
RSS 归档
509人关注
可解群
在数学的历史中,群论原本起源于对五次方程及更高次方程无一般的公式解之证明的找寻,最终随着伽罗瓦理论的提出而确立。可解群的概念产生于描述其根可以只用根式(平方根、立方根等等及其和与积)表示的多项式所对应的自同构群所拥有的性质。
对于有限群,有一个等价的定义为:一可解群为一有着其商群皆为质数目的循环群之合成列的群。此一定义会等价是因为每一个简单阿贝尔群都是有质数目的循环群。若尔当-赫尔德定理表示若一个合成列有此性质,则其循环群即会对应到某个体上的n个根。但此一定义的等价性并不必然于无限群中亦会成立:例如,因为每一个在加法下的整数群Z的非当然子群皆同构于Z本身,它不会有合成列,但是其有着唯一同构于Z的商群之正规列{0,Z},证明了其确实是可解的。
和乔治·波里亚的格言“若有一个你无法算出的问题,则会有的你可以算出的较简单的问题”相一致的,可解群通常在简化有关一复杂的群的推测至一系列有着简单结构-阿贝尔群的群的推测有着很有用的功用。
例子
所有的阿贝尔群都是可解的-其商群A/B总会是可交换的,若A为可交换的。但非阿贝尔群则不一定都是可解的。
群S5不是可解的-它有一合成列{E,A5,S5}(且若尔当-赫尔德定理表示每个其他的合成列都会等价于此一合成列),给出了同构于A5及C2的商群;而A5为非可换的。广义化此一论述,结合An在n > 4时为Sn的正规、最大且非阿贝尔简单子群的事实,可知n > 4的所有Sn皆不可解,此亦为证明每一个n > 4的n次多项式都不可以以方根得解的关键步骤。
著名的范特-汤普逊定理叙述著,每一个奇数目的有限群皆是可解的。特别地是,此定理表示,若一有限群为简单的,其必为质数循环或有偶数目。
性质
可解性的性质在某一意义上是可继承的,如下:
- 若G为可解的,且H为G的子群,则H也是可解的。
- 若G是可解的,且H为G的正规子群,则G/H也是可解的。
- 若G是可解的,且存在一G满射至H的同态,则H也是可解的。
- 若H及G/H为可解的,则G也是可解的。
- 若G及H为可解的,则其直积G×H也是可解的。
做为可解性的加强版,一个群G被称为超可解的,若它有一其商群皆为循环群的不变正规列;换句话说,if it is solvable with each Ai also being a normal subgroup of G,且每个Ai+1/Ai都不只是可交换而已,且也是循环的(可能为无限目)。因为一正规列在定义中有有限的长度,所以不可数阿贝尔群不会是超可解的。实际上,所有的超可解群皆为有限产生群,且一个阿贝尔群为超可解的当且仅当其为有限产生的。
若限制在有限产生群中,将可以有下列的排序:
规范场论
规范场论(Gauge Theory)是基于对称变换可以局部也可以全局地施行这一思想的一类物理理论。非交换对称群的规范场论最常见的例子为杨-米尔斯理论。物理系统往往用在某种变换下不变的拉格朗日量表述,当变换在每一时空点同时施行,它们有全局对称性。规范场论推广了这一思想,它要求拉格朗日量必须也有局部对称性—应该可以在时空的特定区域施行这些对称变换而不影响到另外一个区域。这个要求是广义相对论的等价原理的一个推广。
简史
最早包含规范对称性的物理理论是麦克斯韦的电动力学。但是,该对称性的重要性在早期的表述中没有被注意到。在爱因斯坦发展广义相对论之后,赫尔曼·外尔在试图统一广义相对论和电磁学的尝试中,猜想Eichinvarianz或者说尺度(“规范”)变换下的不变性可能也是广义相对论的局部对称性。后来发现该猜想将导致某些非物理的结果。但是在量子力学发展以后,魏尔、Vladimir Fock和Fritz London实现了该思想,但作了一些修改(把缩放因子用一个复数代替,并把尺度变化变成了相位变化—一个U(1)规范对称性),这对一个相应于带电荷的量子粒子其波函数受到电磁场的影响,给定了一个漂亮的解释。这是第一个规范场论。泡利在1940年推动了该理论的传播。
简史
最早包含规范对称性的物理理论是麦克斯韦的电动力学。但是,该对称性的重要性在早期的表述中没有被注意到。在爱因斯坦发展广义相对论之后,赫尔曼·外尔在试图统一广义相对论和电磁学的尝试中,猜想Eichinvarianz或者说尺度(“规范”)变换下的不变性可能也是广义相对论的局部对称性。后来发现该猜想将导致某些非物理的结果。但是在量子力学发展以后,魏尔、Vladimir Fock和Fritz London实现了该思想,但作了一些修改(把缩放因子用一个复数代替,并把尺度变化变成了相位变化—一个U(1)规范对称性),这对一个相应于带电荷的量子粒子其波函数受到电磁场的影响,给定了一个漂亮的解释。这是第一个规范场论。泡利在1940年推动了该理论的传播。
1950年代,为了解决一些基本粒子物理中的巨大混乱,杨振宁和罗伯特·米尔斯引入非交换规范场论作为理解将核子绑在原子核中的强相互作用的模型。(Ronald Shaw,和Abdus Salam一起工作,在他的博士论文中独立地引入了相同的概念。)通过推广电磁学中的规范不变性,他们试图构造基于(非交换的)SU(2)对称群在同位旋质子和中子对上的作用的理论,类似于U(1)群在量子电动力学的旋量场上的作用。在粒子物理中,重点是使用量子化规范场论。
该思想后来被发现能够用于弱相互作用的量子场论,以及它和电磁学的统一在电弱理论中。当人们意识到非交换规范场论能够导出一个称为渐进自由的特色的时候,规范场论变得更有吸引力,因为渐进自由被认为是强相互作用的一个重要特点—因而推动了寻找强相互作用的规范场论的研究。这个理论现在称为量子色动力学,是一个SU(3)群作用在夸克的色荷上的规范场论。标准模型用规范场论的语言统一了电磁力、弱相互作用和强相互作用的表述。
1970年代迈克尔·阿蒂亚爵士提出了研究经典杨-米尔斯方程的数学解的计划。1983年,Atiyah的学生Simon Donaldson 在这个工作之上证明了光滑4-流形的可微分类和它们只差一个同胚的分类非常不同。Michael Freedman采用Donaldson的工作证明伪R4的存在,也就是,欧几里得4维空间上的奇异微分结构。这导致对于规范场论本身的兴趣,独立于它在基础物理中的成功。1994年,爱德华·威滕和Nathan Seiberg发明了基于超对称的规范场技术,使得特定拓扑不变量的计算成为可能。这些从规范场论来的对数学的贡献导致了对该领域的新兴趣。
一个例子:标量O(n)规范场论
下面解释了局域规范不变性可以从整体对称性质启发式地“导出”,并且解释了它如何导向原来不相互作用的场之间的相互作用。
拉格朗日量可以简明的写作
这是通过引入一个场的矢量
现在很明显地,拉格朗日量在下面的变换中不变
其中Ta矩阵是SO(n)群的生成元。每个生成元有一个守恒流。
不幸的是,G矩阵无法“传递”给导数。当G = G(x),
这意味着定义一个有如下属性的“导数”D
可以验证这样一个“导数”(称为协变导数)是
其中规范场 A(x)定义为有如下变换律的场
而g为耦合常数 - 定义一个相互作用强度的量。
规范场在一点的取值是李代数的一个元素,因此可以展开为
所以相互独立的测度场取值和李代数的生成元一样多。
最后,我们有了一个局域规范不变拉格朗日量

- 泡利把应用到象
 这样的场上的变换称为第一类规范变换,而把
这样的场上的变换称为第一类规范变换,而把 中的补偿变换称为第二类规范变换。
中的补偿变换称为第二类规范变换。

费曼的标量玻色子通过规范玻色子相互作用的示意图
这个拉格朗日量和初始的全局规范不变的拉格朗日量的区别可以视为相互作用拉格朗日量这个项作为要求局部规范不变性的结果而引入了n个标量场之间的相互作用。在这个经典场论的量子化版本中,规范场A(x)的量子称为规范玻色子。相互作用拉格朗日量在量子场论中的解释是标量玻色子通过交换这些规范玻色子来相互作用。规范场的拉格朗日量我们关于经典规范理论的图像基本完成了,还剩协变导数D的定义,为此我们必须知道规范场 A(x) 在所有时空点的值。它可以通过一个场方程的解给出,而不是手工的设置这个场的值。进一步要求产生这个场方程的拉格朗日量也是局部规范不变的,规范场拉格朗日量的最一般的形式可以(传统地)写作其中注意在这个拉格朗日量中,没有一个场 其变换抵消
其变换抵消 的变换。该项在规范变换中的不变性是前面经典(或者说几何,如果喜欢的话)对称性的特殊情况。该对称性必须被限制以施行量子化,这个过程被称为规范固定,但是即使在限制之后,规范变换还是可能的(参看Sakurai, 高等量子力学,1-4节)。O(n)规范场论的拉格朗日量现在成了
的变换。该项在规范变换中的不变性是前面经典(或者说几何,如果喜欢的话)对称性的特殊情况。该对称性必须被限制以施行量子化,这个过程被称为规范固定,但是即使在限制之后,规范变换还是可能的(参看Sakurai, 高等量子力学,1-4节)。O(n)规范场论的拉格朗日量现在成了
- 数学形式化
-
注意,虽然规范理论被联络的研究占据了大部分(主要是因为它主要在高能物理中研究),联络的思想一般不是规范理论的基本或者中心概念。事实上,一般规范理论的一个结果表明规范变换的仿射表示(也就是仿射模)可以分类到一种满足特定属性的节丛的截面。有些表示在每一点共变(物理学家称其为第一类规范变换),有些表示象联络形式一样变换(物理学家称其为第二类规范变换)(注意这是一种仿射表示),还有其它更一般的表示,例如BF理论中的B场。当然,我们可以考虑更一般的表示(实现),但那很复杂。但是,非线性σ模型非线性地变换,所以它们也有用处。我们可以在该主丛上定义一个联络(规范联络),这可以在每个相伴矢量丛上产生一个共变导数∇。若我们选择一个局部标架(截面的局部基),我们就可以用联络形式A表示这个共变导数,A是一个李代数-值的1-形式,在物理学中称为规范势,它显然不是内在的量,而是一个依赖于标架的选择的量。从这个联络形式,我们可以构造曲率形式F,这是一个李代数-值的2-形式,这是一个内在量,定义为其中
 是李括号。一个有趣的结果是,若
是李括号。一个有趣的结果是,若 ,则
,则 其中D是共变导数而且,
其中D是共变导数而且, ,这意味着F共变地变换。杨-米尔斯作用现在可以如下给出
,这意味着F共变地变换。杨-米尔斯作用现在可以如下给出
李群及其代数
数学中,李群是具有群结构的流形或者复流形,并且群中的加法运算和逆元运算是流形中的解析映射。李群在数学分析、物理和几何中都有非常重要的作用。它以索菲斯·李命名。

定义
 均为李群,二者之间的一个同态:
均为李群,二者之间的一个同态: 为群同态并且是解析映射(事实上,可以证明这里解析的条件只需满足连续即可)。显然,两个同态的复合是同态。所有李群的类加上同态构成一个范畴。 两个李群之间存在一个双射,这个双射及其逆射均为同态,就称之为同构。
为群同态并且是解析映射(事实上,可以证明这里解析的条件只需满足连续即可)。显然,两个同态的复合是同态。所有李群的类加上同态构成一个范畴。 两个李群之间存在一个双射,这个双射及其逆射均为同态,就称之为同构。
李代数

定义
 为有限维实解析流形
为有限维实解析流形- 两个解析映射,乘法运算
 ,和逆映射
,和逆映射 满足群公理,从而具有群结构。
满足群公理,从而具有群结构。
 均为李群,二者之间的一个同态:
均为李群,二者之间的一个同态: 为群同态并且是解析映射(事实上,可以证明这里解析的条件只需满足连续即可)。显然,两个同态的复合是同态。所有李群的类加上同态构成一个范畴。 两个李群之间存在一个双射,这个双射及其逆射均为同态,就称之为同构。
为群同态并且是解析映射(事实上,可以证明这里解析的条件只需满足连续即可)。显然,两个同态的复合是同态。所有李群的类加上同态构成一个范畴。 两个李群之间存在一个双射,这个双射及其逆射均为同态,就称之为同构。李代数
- 定义
 对自身的伴随作用 为
对自身的伴随作用 为  ,
, 。
。 - 取 Ad 对变元
 在单位元上的微分,得到李代数上的伴随作用,通常记为
在单位元上的微分,得到李代数上的伴随作用,通常记为  ,
, 。
。 - 再对变元
 微分,得到映射
微分,得到映射  。定义李括积为
。定义李括积为  。
。
不难验证  满足李代数的抽象定义。李括积蕴含了群乘法的无穷小性质,例如:连通李群
满足李代数的抽象定义。李括积蕴含了群乘法的无穷小性质,例如:连通李群  是交换群当且仅当
是交换群当且仅当  是交换李代数。
是交换李代数。
 满足李代数的抽象定义。李括积蕴含了群乘法的无穷小性质,例如:连通李群
满足李代数的抽象定义。李括积蕴含了群乘法的无穷小性质,例如:连通李群  是交换群当且仅当
是交换群当且仅当  是交换李代数。
是交换李代数。
李群对应李代数
若  是李群,
是李群, 是其子群,并带有李群结构,使得包含映射
是其子群,并带有李群结构,使得包含映射  为浸入(不一定是闭的),则可得到子李代数
为浸入(不一定是闭的),则可得到子李代数  。反之,任意子李代数
。反之,任意子李代数  透过左平移定义了
透过左平移定义了  上的叶状结构,取含单位元的极大积分流形,便得到满足前述条件的子群
上的叶状结构,取含单位元的极大积分流形,便得到满足前述条件的子群  。此子群未必是闭子群,它可能是
。此子群未必是闭子群,它可能是  的稠密子集(考虑环面的例子)。
的稠密子集(考虑环面的例子)。
 是李群,
是李群, 是其子群,并带有李群结构,使得包含映射
是其子群,并带有李群结构,使得包含映射  为浸入(不一定是闭的),则可得到子李代数
为浸入(不一定是闭的),则可得到子李代数  。反之,任意子李代数
。反之,任意子李代数  透过左平移定义了
透过左平移定义了  上的叶状结构,取含单位元的极大积分流形,便得到满足前述条件的子群
上的叶状结构,取含单位元的极大积分流形,便得到满足前述条件的子群  。此子群未必是闭子群,它可能是
。此子群未必是闭子群,它可能是  的稠密子集(考虑环面的例子)。
的稠密子集(考虑环面的例子)。
指数映射
对于任意矢量  ,根据常微分方程式的基本理论,存在
,根据常微分方程式的基本理论,存在  中的单参数子群
中的单参数子群  使得
使得  。由此得到的映射
。由此得到的映射
 ,根据常微分方程式的基本理论,存在
,根据常微分方程式的基本理论,存在  中的单参数子群
中的单参数子群  使得
使得  。由此得到的映射
。由此得到的映射
称为指数映射。它总是解析映射。
若  为
为 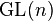 的子群,则
的子群,则  ,这是指数映射一词的缘由。
,这是指数映射一词的缘由。
 为
为 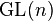 的子群,则
的子群,则  ,这是指数映射一词的缘由。
,这是指数映射一词的缘由。
当  连通且非交换时,指数映射
连通且非交换时,指数映射  并非同态;局部上,
并非同态;局部上, 可以由 Campbell-Baker-Hausdorff 公式表成涉及括积的无穷级数。
可以由 Campbell-Baker-Hausdorff 公式表成涉及括积的无穷级数。
 连通且非交换时,指数映射
连通且非交换时,指数映射  并非同态;局部上,
并非同态;局部上, 可以由 Campbell-Baker-Hausdorff 公式表成涉及括积的无穷级数。
可以由 Campbell-Baker-Hausdorff 公式表成涉及括积的无穷级数。
一般域上的李群
(FromWikipedia)
模形式——五种代数基本运算之一
模形式理论是更广泛的自守形式理论的特例。自守形式理论的发展大致可分成三期:
作为格的函数- 若考虑形如
 之格,其中
之格,其中  为常数而
为常数而  为变量,则
为变量,则  是
是  的全纯函数。
的全纯函数。 - 存在常数
 (通常取正整数),使得对任何
(通常取正整数),使得对任何  ,有
,有  。常数 k 称为此模形式之权。
。常数 k 称为此模形式之权。 - 对于最小非零元与原点距离大于一定值之格
 ,
, 有上界。
有上界。
当 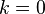 ,条件二表明
,条件二表明  仅决定于
仅决定于  在相似变换下的等价类。这是重要的特例,但是权为零的模形式必为常数函数。若去掉条件三,并容许函数有极点,则存在非常数的例子,称作模函数。
在相似变换下的等价类。这是重要的特例,但是权为零的模形式必为常数函数。若去掉条件三,并容许函数有极点,则存在非常数的例子,称作模函数。
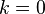 ,条件二表明
,条件二表明  仅决定于
仅决定于  在相似变换下的等价类。这是重要的特例,但是权为零的模形式必为常数函数。若去掉条件三,并容许函数有极点,则存在非常数的例子,称作模函数。
在相似变换下的等价类。这是重要的特例,但是权为零的模形式必为常数函数。若去掉条件三,并容许函数有极点,则存在非常数的例子,称作模函数。
这个状况可以与射影空间  作类比:对于射影空间,我们欲寻找向量空间
作类比:对于射影空间,我们欲寻找向量空间  上对座标的多项式函数
上对座标的多项式函数  ,并满足
,并满足  ;不幸的是,这种函数必为常数。一种办法是容许有分母(即考虑有理函数),则满足条件的是分子、分母为同次数齐次多项式的有理函数。另一种办法则是修改条件
;不幸的是,这种函数必为常数。一种办法是容许有分母(即考虑有理函数),则满足条件的是分子、分母为同次数齐次多项式的有理函数。另一种办法则是修改条件  为
为  ,则满足此条件的函数为
,则满足此条件的函数为  次齐次多项式,对每个固定的
次齐次多项式,对每个固定的  ,这些函数构成有限维向量空间。借着考虑所有可能的
,这些函数构成有限维向量空间。借着考虑所有可能的  ,我们可以找出构造
,我们可以找出构造  上的有理函数所需之分子与分母。
上的有理函数所需之分子与分母。
 作类比:对于射影空间,我们欲寻找向量空间
作类比:对于射影空间,我们欲寻找向量空间  上对座标的多项式函数
上对座标的多项式函数  ,并满足
,并满足  ;不幸的是,这种函数必为常数。一种办法是容许有分母(即考虑有理函数),则满足条件的是分子、分母为同次数齐次多项式的有理函数。另一种办法则是修改条件
;不幸的是,这种函数必为常数。一种办法是容许有分母(即考虑有理函数),则满足条件的是分子、分母为同次数齐次多项式的有理函数。另一种办法则是修改条件  为
为  ,则满足此条件的函数为
,则满足此条件的函数为  次齐次多项式,对每个固定的
次齐次多项式,对每个固定的  ,这些函数构成有限维向量空间。借着考虑所有可能的
,这些函数构成有限维向量空间。借着考虑所有可能的  ,我们可以找出构造
,我们可以找出构造  上的有理函数所需之分子与分母。
上的有理函数所需之分子与分母。
作为椭圆曲线模空间上的函数
每个格  都决定一条复椭圆曲线
都决定一条复椭圆曲线  ;两个格给出的椭圆曲线同构的充要条件是两个格之间差一个非零复数的倍数。因此模函数可以看作是复椭圆曲线的模空间上的函数。例如椭圆曲线的j-不变量就是模函数。模形式可视作模空间上某些线丛的截面。
;两个格给出的椭圆曲线同构的充要条件是两个格之间差一个非零复数的倍数。因此模函数可以看作是复椭圆曲线的模空间上的函数。例如椭圆曲线的j-不变量就是模函数。模形式可视作模空间上某些线丛的截面。
 都决定一条复椭圆曲线
都决定一条复椭圆曲线  ;两个格给出的椭圆曲线同构的充要条件是两个格之间差一个非零复数的倍数。因此模函数可以看作是复椭圆曲线的模空间上的函数。例如椭圆曲线的j-不变量就是模函数。模形式可视作模空间上某些线丛的截面。
;两个格给出的椭圆曲线同构的充要条件是两个格之间差一个非零复数的倍数。因此模函数可以看作是复椭圆曲线的模空间上的函数。例如椭圆曲线的j-不变量就是模函数。模形式可视作模空间上某些线丛的截面。
例如,取  :
:
 :
:
如果上述方程仅对  内的某个有限指数子群
内的某个有限指数子群  成立,则称
成立,则称  为对
为对  的模形式。最常见的例子是同余子群
的模形式。最常见的例子是同余子群  ,以下将详述。
,以下将详述。
 内的某个有限指数子群
内的某个有限指数子群  成立,则称
成立,则称  为对
为对  的模形式。最常见的例子是同余子群
的模形式。最常见的例子是同余子群  ,以下将详述。
,以下将详述。
广义定义
及任何属于上半平面的  ,有
,有
 ,有
,有
而且  在尖点全纯。所谓尖点,是
在尖点全纯。所谓尖点,是  在
在  作用下的轨道。例如当
作用下的轨道。例如当  时,
时, 代表了唯一的尖点。模形式在尖点
代表了唯一的尖点。模形式在尖点  全纯,意谓
全纯,意谓  时
时  有界。当此尖点为
有界。当此尖点为  时,这等价于
时,这等价于  有傅立叶展开式
有傅立叶展开式
 在尖点全纯。所谓尖点,是
在尖点全纯。所谓尖点,是  在
在  作用下的轨道。例如当
作用下的轨道。例如当  时,
时, 代表了唯一的尖点。模形式在尖点
代表了唯一的尖点。模形式在尖点  全纯,意谓
全纯,意谓  时
时  有界。当此尖点为
有界。当此尖点为  时,这等价于
时,这等价于  有傅立叶展开式
有傅立叶展开式
其中  。对于其它尖点,同样可藉座标变换得到傅立叶展开。
。对于其它尖点,同样可藉座标变换得到傅立叶展开。
 。对于其它尖点,同样可藉座标变换得到傅立叶展开。
。对于其它尖点,同样可藉座标变换得到傅立叶展开。
另一种的推广是考虑某类函数  ,并将函数方程改写为
,并将函数方程改写为
 ,并将函数方程改写为
,并将函数方程改写为
上式所取的  称为自守因子。若另取适当的
称为自守因子。若另取适当的  ,则在此框架下亦可探讨戴德金η函数,这是权等于 1/2 的模形式。例如:一个权等于
,则在此框架下亦可探讨戴德金η函数,这是权等于 1/2 的模形式。例如:一个权等于  、
、 级、nebentypus 为
级、nebentypus 为  (
( 是模
是模  的一个狄利克雷特征)是定义于上半平面,并具下述性质的全纯函数:对任意
的一个狄利克雷特征)是定义于上半平面,并具下述性质的全纯函数:对任意
 称为自守因子。若另取适当的
称为自守因子。若另取适当的  ,则在此框架下亦可探讨戴德金η函数,这是权等于 1/2 的模形式。例如:一个权等于
,则在此框架下亦可探讨戴德金η函数,这是权等于 1/2 的模形式。例如:一个权等于  、
、 级、nebentypus 为
级、nebentypus 为  (
( 是模
是模  的一个狄利克雷特征)是定义于上半平面,并具下述性质的全纯函数:对任意
的一个狄利克雷特征)是定义于上半平面,并具下述性质的全纯函数:对任意
及属于上半平面的  ,有函数方程
,有函数方程
 ,有函数方程
,有函数方程
此外, 必须在尖点全纯。
必须在尖点全纯。
 必须在尖点全纯。
必须在尖点全纯。
例子
艾森斯坦级数
模形式最简单的例子是艾森斯坦级数:对每个偶数  2">,定义
2">,定义
 2">,定义
2">,定义
(条件  2"> 用于确立收敛性
2"> 用于确立收敛性
 2"> 用于确立收敛性
2"> 用于确立收敛性
theta函数
是权  的模形式。偶单位模格的构造并不容易,以下是方法之一:令
的模形式。偶单位模格的构造并不容易,以下是方法之一:令  为 8 的倍数,并考虑所有向量
为 8 的倍数,并考虑所有向量  ,使得
,使得  的座标均为奇数或均为偶数,且
的座标均为奇数或均为偶数,且  的各座标总和为奇数。由此构成的格写作
的各座标总和为奇数。由此构成的格写作  。当
。当 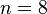 ,此格由根系
,此格由根系  的根生成。虽然
的根生成。虽然  与
与  并不相似,由于权
并不相似,由于权  的模形式只有一个(至多差一个常数倍),遂得到
的模形式只有一个(至多差一个常数倍),遂得到
 的模形式。偶单位模格的构造并不容易,以下是方法之一:令
的模形式。偶单位模格的构造并不容易,以下是方法之一:令  为 8 的倍数,并考虑所有向量
为 8 的倍数,并考虑所有向量  ,使得
,使得  的座标均为奇数或均为偶数,且
的座标均为奇数或均为偶数,且  的各座标总和为奇数。由此构成的格写作
的各座标总和为奇数。由此构成的格写作  。当
。当 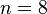 ,此格由根系
,此格由根系  的根生成。虽然
的根生成。虽然  与
与  并不相似,由于权
并不相似,由于权  的模形式只有一个(至多差一个常数倍),遂得到
的模形式只有一个(至多差一个常数倍),遂得到
戴德金伊塔函数
戴德金η函数定义为
数学物理中的一类重要函数——贝塞尔函数(From Wikipedia)
贝塞尔函数(Bessel functions),是数学上的一类特殊函数的总称。通常单说的贝塞尔函数指第一类贝塞尔函数(Bessel function of the first kind)。一般贝塞尔函数是下列常微分方程(一般称为贝塞尔方程)的标准解函数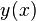 :
:
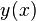 :
:
这类方程的解是无法用初等函数系统地表示。
贝塞尔函数的具体形式随上述方程中任意实数或复数α变化而变化(相应地,α被称为其对应贝塞尔函数的阶数)。实际应用中最常见的情形为α是整数n,对应解称为n 阶贝塞尔函数。
尽管在上述微分方程中,α本身的正负号不改变方程的形式,但实际应用中仍习惯针对α和−α定义两种不同的贝塞尔函数(这样做能带来好处,比如消除了函数在α=0 点的不光滑性)。
贝塞尔方程是在圆柱坐标或球坐标下使用分离变量法求解拉普拉斯方程和亥姆霍兹方程时得到的(在圆柱域问题中得到的是整阶形式 α = n;在球形域问题中得到的是半奇数阶形式 α = n+½),因此贝塞尔函数在波动问题以及各种涉及有势场的问题中占有非常重要的地位,最典型的问题有:
第一类贝塞尔函数
第一类贝塞尔函数(Bessel function of the first kind),又称贝塞尔函数(Bessel function),下文中有时会简称为J函数,记作Jα。
第一类α阶贝塞尔函数Jα(x)是贝塞尔方程当α为整数或α非负时的解,须满足在x = 0 时有限。这样选取和处理Jα的原因见本主题下面的性质介绍;另一种定义方法是通过它在x = 0 点的泰勒级数展开(或者更一般地通过幂级数展开,这适用于α为非整数):
上式中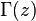 为Γ函数(它可视为阶乘函数向非整型自变量的推广)。第一类贝塞尔函数的形状大致与按
为Γ函数(它可视为阶乘函数向非整型自变量的推广)。第一类贝塞尔函数的形状大致与按 速率衰减的正弦或余弦函数类似(参见本页下面对它们渐进形式的介绍),但它们的零点并不是周期性的,另外随着x的增加,零点的间隔会越来越接近周期性。图2所示为0阶、1阶和2阶第一类贝塞尔函数
速率衰减的正弦或余弦函数类似(参见本页下面对它们渐进形式的介绍),但它们的零点并不是周期性的,另外随着x的增加,零点的间隔会越来越接近周期性。图2所示为0阶、1阶和2阶第一类贝塞尔函数 的曲线(
的曲线( )。
)。
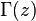 为Γ函数(它可视为阶乘函数向非整型自变量的推广)。第一类贝塞尔函数的形状大致与按
为Γ函数(它可视为阶乘函数向非整型自变量的推广)。第一类贝塞尔函数的形状大致与按 速率衰减的正弦或余弦函数类似(参见本页下面对它们渐进形式的介绍),但它们的零点并不是周期性的,另外随着x的增加,零点的间隔会越来越接近周期性。图2所示为0阶、1阶和2阶第一类贝塞尔函数
速率衰减的正弦或余弦函数类似(参见本页下面对它们渐进形式的介绍),但它们的零点并不是周期性的,另外随着x的增加,零点的间隔会越来越接近周期性。图2所示为0阶、1阶和2阶第一类贝塞尔函数 的曲线(
的曲线( )。
)。
如果α不为整数,则 和
和 线性无关,可以构成微分方程的一个解系。反之若
线性无关,可以构成微分方程的一个解系。反之若 是整数,那么上面两个函数之间满足如下关系:
是整数,那么上面两个函数之间满足如下关系:
 和
和 线性无关,可以构成微分方程的一个解系。反之若
线性无关,可以构成微分方程的一个解系。反之若 是整数,那么上面两个函数之间满足如下关系:
是整数,那么上面两个函数之间满足如下关系:
于是两函数之间已不满足线性无关条件。为寻找在此情况下微分方程与 线性无关的另一解,需要定义第二类贝塞尔函数,定义过程将在后面的小节中给出。
线性无关的另一解,需要定义第二类贝塞尔函数,定义过程将在后面的小节中给出。
 线性无关的另一解,需要定义第二类贝塞尔函数,定义过程将在后面的小节中给出。
线性无关的另一解,需要定义第二类贝塞尔函数,定义过程将在后面的小节中给出。
贝塞尔积分
 为整数时贝塞尔函数的另一种定义方法由下面的积分给出:
为整数时贝塞尔函数的另一种定义方法由下面的积分给出:
( 为任意实数时的表达式见参考文献[2]第360页)
为任意实数时的表达式见参考文献[2]第360页)
 为任意实数时的表达式见参考文献[2]第360页)
为任意实数时的表达式见参考文献[2]第360页)
这个积分式就是贝塞尔当年提出的定义,而且他还从该定义中推出了函数的一些性质。另一种积分表达式为:

- 和超几何函数的关系
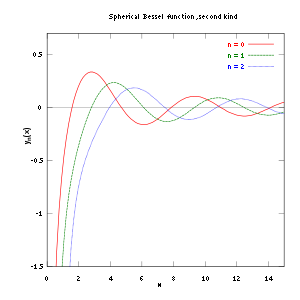
- 贝塞尔函数可以用超几何级数表示成下面的形式:ɑ为整数。由于函数线性相关的特性(用了一个就少了一个,所以要再构造一个),才需定义如下详细介绍的第二类贝塞尔函数。第二类贝塞尔函数(诺依曼函数)第二类贝塞尔函数(Bessel function of the second kind),又称诺伊曼函数(Neumann function),下文中有时会简称为Y函数,记作Yα。第二类贝塞尔函数也许比第一类更为常用。 这种函数通常用Yα(x)表示,它们是贝塞尔方程的另一类解。x = 0 点是第二类贝塞尔函数的(无穷)奇点。Yα(x)又被称为诺依曼函数(Neumann function),有时也记作Nα(x)。它和Jα(x)存在如下关系:从前面对Jα(x)的定义可以知道,若α不为整数时,定义Yα是多余的(因为贝塞尔方程的两个线性无关解都已经用J函数表示出来了)。另一方面,若α为整数,Yα便可以和Jα构成贝塞尔方程的一个解系。与J函数类似,Y函数正负整数阶之间也存在如下关系:Jα(x)和Yα(x)均为沿负实半轴割开的复平面内关于x的全纯函数。当α为整数时,复平面内不存在贝塞尔函数的支点,所以J 和Y 均为x 的整函数。若将x 固定,则贝塞尔函数是α的整函数。图3所示为0阶、1阶和2阶第二类贝塞尔函数
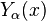 的曲线(
的曲线( ):
): 第三类贝塞尔函数(汉克尔函数)第三类贝塞尔函数(Bessel function of the third kind),又称汉克尔函数(Hankel function)。贝塞尔方程的另外一对重要的线性无关解称为汉克尔函数(Hankel functions)Hα(1)(x)和Hα(2)(x),分别定义为:利用前面推出的关系可将汉克尔函数表示成:若α为整数,则须对等号右边取极限值。另外,无论α是不是整数,下面的关系都成立:
第三类贝塞尔函数(汉克尔函数)第三类贝塞尔函数(Bessel function of the third kind),又称汉克尔函数(Hankel function)。贝塞尔方程的另外一对重要的线性无关解称为汉克尔函数(Hankel functions)Hα(1)(x)和Hα(2)(x),分别定义为:利用前面推出的关系可将汉克尔函数表示成:若α为整数,则须对等号右边取极限值。另外,无论α是不是整数,下面的关系都成立:
- 变形贝塞尔函数
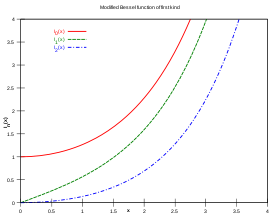
- 贝塞尔函数当变量x 为复数时同样成立,并且当x 为纯虚数时能得到一类重要情形——它们被称为变形第一类贝塞尔函数(modified Bessel function of the first kind)和变形第二类贝塞尔函数(modified Bessel function of the second kind),或虚变量的贝塞尔函数(有时还称为双曲型贝塞尔函数),定义为:以上形式保证了当变量x 为实数时,函数值亦为实数。这两个函数构成了下列变形贝塞尔方程(与一般贝塞尔方程的差别仅在两个正负号)的一个相互线性无关的解系:变形贝塞尔函数与一般贝塞尔函数的差别在于:一般贝塞尔函数随实变量是振荡型的,而变形贝塞尔函数Iα 和Kα则分别是指数增长和指数衰减型的。和第一类贝塞尔函数Jα一样,函数Iα当α > 0 时在x=0 点等于0,当α=0时在x=0 点趋于有限值。类似地,Kα在x=0 点发散(趋于无穷)。
 球形贝塞尔函数关于上述方程的一对线性无关解称为球贝塞尔函数,分别用jn和yn表示(有时也记为nn)。这两个函数与一般贝塞尔函数Jn和Yn 存在关系:球贝塞尔函数也可写成:0阶第一类球贝塞尔函数
球形贝塞尔函数关于上述方程的一对线性无关解称为球贝塞尔函数,分别用jn和yn表示(有时也记为nn)。这两个函数与一般贝塞尔函数Jn和Yn 存在关系:球贝塞尔函数也可写成:0阶第一类球贝塞尔函数 又称为sinc函数。头几阶整阶球贝塞尔函数的表达式分别为:第一类:第二类:还可以依照前面构造汉克尔函数相同的步骤构造所谓 球汉克尔函数:事实上,所有半奇数阶贝塞尔函数都可以写成由三角函数组成的封闭形式的表达式,球贝塞尔函数也同样可以。特别地,对所有非负整数n,存在:而对实自变量x,hn(2)是上面hn(1)的复共轭(!! 表示双阶乘)。由此我们可以通过得到h,再分离实部虚部,求出相应阶j 和h 的表达式,譬如j0(x) = sin(x)/x,y0(x) = -cos(x)/x,等等。
又称为sinc函数。头几阶整阶球贝塞尔函数的表达式分别为:第一类:第二类:还可以依照前面构造汉克尔函数相同的步骤构造所谓 球汉克尔函数:事实上,所有半奇数阶贝塞尔函数都可以写成由三角函数组成的封闭形式的表达式,球贝塞尔函数也同样可以。特别地,对所有非负整数n,存在:而对实自变量x,hn(2)是上面hn(1)的复共轭(!! 表示双阶乘)。由此我们可以通过得到h,再分离实部虚部,求出相应阶j 和h 的表达式,譬如j0(x) = sin(x)/x,y0(x) = -cos(x)/x,等等。
 渐进形式贝塞尔函数在α非负时具有下面的渐近形式。当自变量x 为小量,即
渐进形式贝塞尔函数在α非负时具有下面的渐近形式。当自变量x 为小量,即 时,有:(α=1/2 时渐近号两边严格相等;参见前面对球贝塞尔函数的介绍)。其他形式贝塞尔函数的渐近形式可以从上面的式子直接推得。譬如,对大自变量
时,有:(α=1/2 时渐近号两边严格相等;参见前面对球贝塞尔函数的介绍)。其他形式贝塞尔函数的渐近形式可以从上面的式子直接推得。譬如,对大自变量 ,修正贝塞尔函数的渐近形式为:对小自变量
,修正贝塞尔函数的渐近形式为:对小自变量 :
:- 性质
-
上式得左边即为整阶第一类贝塞尔函数的母函数,这是丹麦天文学家汉森于1843年提出的。(这种定义也可以通过路径积分或其他方法推广到非整数阶)。整阶函数的另一个重要性质是下列雅可比-安格尔恒等式(Jacobi-Anger identity):函数Jα、Yα、Hα(1)和Hα(2)均满足递推关系:其中α > -1,δm,n为克罗内克δ,uα,m表示Jα(x)的第m 级零点。这个正交性关系可用于计算傅里叶-贝塞尔级数中各项的系数,以利用该级数将任意函数写成α固定、m 变化的函数Jα(x uα,m)的无穷叠加形式。(可以立即得到球贝塞尔函数相应的关系)。另一个正交性关系是下列在α > -1/2时成立的“封闭方程”(closure equation):其中δ为狄拉克δ函数。球贝塞尔函数的正交性条件为(当α > 0):其中Aα 和Bα是贝塞尔方程的任意两个解,Cα是与x 无关的常数(由α和贝塞尔函数的种类决定)。譬如,若Aα = Jα、Bα = Yα,则Cα is 2/π。该性质在修正贝塞尔函数中同样适用,譬如,若Aα = Iα、Bα = Kα,则Cα为-1。
我国科学家率先证明引力场以光速传播

汤克云2011年在中科院演讲(资料图)
前天下午,“引力场以光速传播的观测证据”新闻发布会在京举行,汤克云等宣布成功获得全球首个“引力场以光速传播”的观测证据。相关论文已发表于最新一期的《Chinese Science Bulletin》(中国科学通报)上。
牛顿认为引力传播是一种超距作用,也就是说引力可以在瞬间传播至任意远处,这种认识非常符合日常生活中引力无处不在的个人体验。但爱因斯坦1918年提出的广义相对论预言,引力不存在超距作用,而是以光速传播的波,并形成引力场。通俗地讲,引力场与引力波有些类似电磁场与电磁波的关系。
引力波探测,除了能够验证爱因斯坦广义相对论的正确性外,还有助于证明其他各种引力理论的正确与否,推动引力场量子化的理论研究。这些都是现代物理学的重要课题,如果出现与预期不符的结果,将有可能导致物理学的又一次大发展。
中国科学家的这项创新突破,实现了物理学界多年来对通过实验或观测获得引力场传播速度的期待。中科院院士滕吉文说:“这项原创成果是中国科学家在引力物理研究领域的重要突破。”
十年漫漫探索路
由中国科学院地质与地球物理研究所的汤克云研究员领衔、中国地震局和中国科学院大学有关科研人员组成的科学团队,经过10多年的持续探索,在实施多次日食期间的重力固体潮观测后,发现地球固体潮公式实际上暗含着引力场以光速传播的假定,从而提出用固体潮测量引力传播速度的方法。
该团队先后利用的日食是:1997年漠河日全食、2001年赞比亚日全食、2002年澳大利亚日全食、2008年嘉峪关日全食、2009年上海—杭州—湖州日全食和2010年云南大理日环食。

2009年杭州日食景观
汤克云科学团组随后选择远离太平洋、大西洋、印度洋和北冰洋的西藏狮泉河站和新疆乌什站的固体潮数据,以避免海洋潮汐的影响。他们滤去了数据的扰动,再把数据代入引力传播速度方程,证明方程成立。也就是说,最终获得了全球第一个能证明“引力场以光速传播”的观测证据。数据显示引力波的传播速度为0.93至1.05倍光速,误差为5%。

日全食期间测量用的真空摆,安置于上海佘山
相关知识介绍:
引力场与引力波的探测
最常见的探测引力波的方法是观测大质量天体,因为它们的运动会发射出较大的引力波辐射。例如白矮星、中子星或黑洞等组成的双星系统,河外星系内合并形成的超大质量黑洞,自转的脉冲星的自转,超新星的引力坍缩等。

正在融合的两个黑洞是强大的引力波源(模拟图)
科学家通常用激光干涉仪来探测。但引力本身非常微小,比电磁力小三四十个量级。据估计,引力波使激光光程差产生的变化,大约只有一个质子的大小。因此,即使在真空和隔离振动的环境下,也极难探测到。汤克云团队曾于2004年筹划建立低频的中国爱因斯坦引力波探测站(CEGO),作为国际上高频探测的补充,《科学》杂志曾予以报道。
2011年8月,科学家在德国汉诺威的GEO600引力波观测站和意大利比萨的处女座引力波探测器获得了引力波存在的证据,但未证实“引力波以光速传播”。
固体潮
通常指在日、月引潮力的作用下,固体地球产生的周期性形变的现象。月球和太阳对地球的引力不但可以引起地球表面流体的潮汐,还能引起地球固体部分的周期性形变。由于其他天体距地球甚远,对地球的引力甚微,在固体潮的研究中一般可略而不计。

测量重力异常用的部分实验设备
转自 PLASS|科学|发布
统一理论中的数论——圈量子引力理论
圈量子引力论(loop quantum gravity,LQG),又译回圈量子重力论,英文别名圈引力(loop gravity)及量子几何学(quantum geometry);由阿贝·阿希提卡(Ahbay Ashtekar)、李·施莫林(Lee Smolin)、卡洛·洛华利(Carlo Rovelli)等人发展出来的量子引力理论,与弦理论一并是目前为止将引力论量子化最成功的理论。
利用量子场论的微扰理论来实现引力论的量子化的理论是不能被重整化的。如果主张时空只有四维,从广义相对论下手,结果可以把广义相对论转变成类似规范场论的理论,基本正则变量为阿希提卡-巴贝罗联络(Ashtekar-Barbero Connection)而非度规张量,再以联络定义的平移算子(holonomy)以及通量变数(flux variable)为基本变量实现量子化。
在此理论下,时空描述是呈背景独立,由关系性循环织成的自旋网络铺成时空几何。网络中每条边及每个节点分别为一普朗克长度及普朗克体积。循环并不存在于时空中,循环扭结的方式定义时空几何。在普朗克尺度下,时空几何充满随机的量子涨落,因此自旋网络又称为自旋泡沫(Spin foam)。在此理论下,时空是离散的。
圈量子引力通论及目标
多数弦论学家相信无法在3+1维时空中,将引力量子化而不产生物质与能量有关的人工产物。然而弦论所预测的物质有关的人工产物也未被证明是否真的与实际观测到的物质不相同。不过若圈量子引力成功地成为引力的量子理论,则已知的物质场必须“事后”再加到此一理论中,而不是从理论中自然而然地出现。圈量子引力论的创始者之一李·施莫林已思索过弦论与圈量子引力两者可能分别是一个终极理论两相不同的近似这样的可能性。

圈量子理论中使用的简单的自旋网络形态
目前圈量子引力声称具有的成功之处有:
然而,这样的声称尚未被完全接受。虽然许多圈量子引力的核心成果都是来自于严谨的数学物理,不过它们的物理诠释仍多为推敲性质。圈量子引力是有可能成为引力或者是几何的改进方案;举例来说,(2)中的熵计算事实上是针对一种形式的“洞”来做的,这个洞可能是,也可能不是黑洞。
量子引力的其他方案,比如自旋泡沫模型,与圈量子引力密切相关。
圈量子引力的假设
圈量子引力的两个最重要的假设为
圈量子引力也假设量子论的基本原理是正确的。举例广义协变的理论有广义相对论,非广义协变的理论有狭义相对论(狭义协变),非背景独立的理论有牛顿力学(假设存在一条独立不变的时间轴),狭义相对论(其背景为闵可夫斯基空间,背景度规为闵可夫斯基度规),在背景电磁场中运动的电子的方程等,背景独立的理论有广义相对论,度规张量的值完全由理论决定。
量子力学与广义相对论的不相容
量子力学与广义相对论是20世纪最具革命性的两大理论,但两者却互不兼容。广义相对论研究大尺度的物体,而量子力学则掌管着亚原子粒子的微观世界,一个具有定域性,而另一个则不具备。所以我们需要一个完备的量子引力理论来统一广义相对论与量子力学,就像电弱统一理论很好地把电磁力与弱相互作用力合并在一起那样。目前有许多的候选理论,如弦论,圈量子引力论,标度相对论。
圈量子引力理论的基本内容
阿西提卡—巴贝罗联络
此时用卡当的几何法,用三足(triad)一次型来表示度规张量,


即阿希提卡-巴贝罗联络。其正则动量为 。使用狄拉克约束处理方法可得三个第一类约束:
。使用狄拉克约束处理方法可得三个第一类约束:
 。使用狄拉克约束处理方法可得三个第一类约束:
。使用狄拉克约束处理方法可得三个第一类约束:Riemann ζ Function——素数的音乐
在区域{s : Re(s) > 1}上, 此无穷级数收敛并为一全纯函数。(上式中Re表示复数的实部。)。欧拉在1740考虑过s为正整数的情况,后来切比雪夫拓展到s>1。[1] 波恩哈德·黎曼认识到:ζ函数可以通过解析开拓来扩展到一个定义在复数域(s, s≠ 1)上的全纯函数ζ(s)。这也是黎曼猜想所研究的函数。
虽然黎曼的ζ函数被数学家认为主要和“最纯”的数学领域数论相关,它也出现在应用统计学中(参看齐夫定律(Zipf's Law)和齐夫-曼德尔布罗特定律(Zipf-Mandelbrot Law)),还有物理,以及调音的数学理论中。
和素数的关系
我们可以用莫比乌斯函数μ(n)表达ζ函数的倒数如下
对于所有实部>1的复数s。这和上面ζ(2)的表达式一起可以用来证明两个随机整数互质的概率是6/π2。
函数值
ζ函数满足如下函数方程:
当s为正整数
欧拉也能计算ζ(2k),对于偶整数2k,他使用公式
其中B2k是伯努利数。从这个,我们可以看到ζ(2) = π2/6, ζ(4) = π4/90, ζ(6) = π6/945等等。(序列A046988/A002432列在OEIS)。这些给出了著名的π的无穷级数。奇整数的情况没有这么简单。拉马努金在这上面做了很多了不起的工作。  为正偶数时的函数值公式已经由欧拉计算出。但当
为正偶数时的函数值公式已经由欧拉计算出。但当 为正奇数时,尚未找到封闭式。
为正奇数时,尚未找到封闭式。
 为正偶数时的函数值公式已经由欧拉计算出。但当
为正偶数时的函数值公式已经由欧拉计算出。但当 为正奇数时,尚未找到封闭式。
为正奇数时,尚未找到封闭式。
- 这是调和级数。
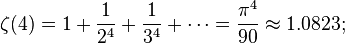 (OEIS中的数列A0013662)
(OEIS中的数列A0013662)
- 黑体辐射里的斯特藩-玻尔兹曼定律和维恩近似。
负整数
同样由欧拉发现,ζ函数在负整数点的值是有理数,这在模形式中发挥着重要作用。
复数值
 ,x>1。
,x>1。
幅角
![\arg[\zeta(x+{\rm{i}}y)]=-\arctan\frac{\sum_{k=1}^{\infty}\frac{\sin(y\ln k)}{k^x}}{\sum_{k=1}^{\infty}\frac{\cos(y\ln k)}{k^x}}](http://upload.wikimedia.org/math/9/9/f/99f102a1d32372cb38a49acbfbf69cb5.png)
函数值表
 ,
, ,
, ,
,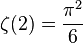 ,
,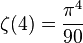 ,
, ,
, ,
,
当代最伟大的物理学家——爱德华威腾(From Wikipedia)
爱德华·威滕(Edward Witten,姓氏亦译为维腾、维敦或惠滕,1951年8月26日-)是犹太裔美国数学物理学家、菲尔兹奖得主,也是普林斯顿高等研究院教授。他是弦理论和量子场论的顶尖专家,创立了M理论。爱德华·威滕被视为当代最伟大的物理学家之一,他的一些同行甚至认为他是爱因斯坦的后继者之一。国际数学联盟于1990年授予他菲尔兹奖,是数学界的最高荣誉,相当于数学界的诺贝尔奖。爱德华·威滕也是唯一获得这项荣誉的物理学家 。
生平
生平
威滕生于美国马里兰州巴尔的摩。父亲路易斯·威滕(Louis Witten)是研究广义相对论的理论物理学家,母亲是洛兰·沃拉克·威滕(Lorraine W. Witten)。威滕原先就读于约翰·霍普金斯大学,在转学布兰代斯大学获得历史学学士学位后(辅修新闻学),曾参与民主党候选人乔治·麦戈文(George McGovern)的总统竞选工作一段短时间,后来乔治·麦戈文败给理查德·尼克松。
他于1976年获得普林斯顿大学应用数学博士学位,导师是戴维·格娄斯。在此之后,威滕先后任职于哈佛大学初级研究员(Junior Fellow)和普林斯顿大学教授。他现在是普林斯顿高等研究院的查尔斯·希莫尼数学物理学教授。
研究
威滕对理论物理学做出广泛的贡献,也促进大量重要的数学进展。他已经出版超过350部著作,主要是量子场论、弦理论、拓扑和几何形状的相关领域。威滕被他的同行们广泛认为是20世纪最重要的理论物理学家之一。虽然在某些方面很难将他的深刻贡献加以归类,威滕于物理方面的贡献侧重于超对称,于数学方面则是拓扑结构。
威滕在物理学的早期贡献之一是所谓级列问题(hierarchy problem)的解决方案。粒子物理学的标准模型预言一种被称为希格斯玻色子的存在。然而它的质量似乎比模型预测的数字还要轻得多。威滕认为,超对称破坏的机制提供了级列问题一种的自然解释。在超对称理论中,威滕指数(Witten index)用来判断超对称是否遭到破坏。威滕在超对称规范理论仍然继续做出开创性的贡献。他与普林斯顿高等研究院内森·塞伯格(Nathan Seiberg)发展出塞伯格-威滕理论。
威滕显然是弦理论的代表人物,这是一个用来说明所有自然力的理论。甚至早在1984年,威滕引力异常做出重要贡献,为为第一次弦理论革命铺平了道路。1990年代中期在南加州大学弦理论会议中,威滕推测存在一个统一的理论还没有被发现,称之为M理论。M理论可能是宇宙物理理论最根本的理论。英国物理学家斯蒂芬·霍金在他的著作《大设计》(The Grand Design)中,认为M理论可能是宇宙的终极理论。
爱德华·威滕其他重要物理学的贡献包括引力二重性。1997年,阿根廷理论物理学家胡安·马尔达西那首先提出了在反德希特空间背景下某些超引力理论和边界上共形场论的对偶关系,即AdS/CFT对应猜想。这一革命性的发现为过去15年中占据了理论物理的主导地位,对于威滕的研究产生非常重要的影响。
国际数学联盟在1990年授予威滕菲尔兹奖,成为第一位获得该奖项的物理学家(也是唯一一位)。他对纯数学方面的研究影响深远,例如他使用琼斯多项式(Jones Polynomial)来解释陈-西门斯理论”(Chern-Simons theory)。这项研究对于低维拓扑结构有深远影响,并推导出量子不变量。
威滕被认为是他的世代中最优秀的物理学家,也被认为是世界上最伟大的物理学家之一,也许甚至是爱因斯坦的后继者。在1995年,他在南加州大学会议中提出M理论,并用它来解释一些以前观察到的现象,在弦论中引发所谓的第二次超弦革命。
评价
威滕具有深刻的物理直觉和高超的数学能力。他专长量子场论、弦理论和拓扑与几何相关的范围。他的主要贡献包括广义相对论的正能定理证明、超对称和莫尔斯理论、拓扑量子场论、超弦紧化、镜像对称、超对称规范场论和对M理论存在性的猜想。
威滕受到许多同行的广泛赞赏,数学家迈克尔·阿蒂亚曾说:
| “ |
虽然他肯定是物理学家,不过他对数学的掌握很少数学家能比得上……他一次又一次超越了数学界,以巧妙的物理直觉导出新颖深刻的数学定理……他对现代数学影响巨大……凭着他物理再次成为数学的丰富灵感和直觉源头。
| ” |
智者的游戏——博弈论
博弈论(Game theory),有时也称为对策论,或者赛局理论,应用数学的一个分支,目前在生物学、经济学、国际关系、计算机科学、政治学、军事战略和其他很多学科都有广泛的应用。主要研究公式化了的激励结构(游戏或者博弈)间的相互作用。是研究具有斗争或竞争性质现象的数学理论和方法。也是运筹学的一个重要学科。
概述
概述
博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。表面上不同的相互作用可能表现出相似的激励结构(incentive structure),所以他们是同一个游戏的特例。其中一个有名有趣的应用例子是囚徒困境。
具有竞争或对抗性质的行为成为博弈行为。在这类行为中,参加斗争或竞争的各方各自具有不同的目标或利益。为了达到各自的目标和利益,各方必须考虑对手的各种可能的行动方案,并力图选取对自己最为有利或最为合理的方案。比如日常生活中的下棋,打牌等。博弈论就是研究博弈行为中斗争各方是否存在着最合理的行为方案,以及如何找到这个合理的行为方案的数学理论和方法。
生物学家使用博弈理论来理解和预测进化(论)的某些结果。例如,John Maynard Smith 和George R. Price 在1973年发表于《自然》杂志上的论文中提出的“evolutionarily stable strategy”的这个概念就是使用了博弈理论。还可以参见进化博弈理论(evolutionary game theory)和行为生态学(behavioral ecology)。
数学定义
范式博弈
范式博弈又被译为正则形式的博弈、策略型赛局或标准型赛局。
也就是说,如果我们知道了参与者的策略集合是什么,那么就可以有一个实数值与之对应。 我们可以把上面的方程拆成两个方程来进一步把它一般化。一个方程是正则形式(Normal form game)的参与者程,描述策略规定结果的方式。 另外一个方程描写参与者对于结果(outcome)集合的偏好(preference)。也就是:
这里  是游戏(博弈)的结果集合(outcome set)。对于每一个参与者
是游戏(博弈)的结果集合(outcome set)。对于每一个参与者 都有一个偏好函数( preference function)
都有一个偏好函数( preference function)
 是游戏(博弈)的结果集合(outcome set)。对于每一个参与者
是游戏(博弈)的结果集合(outcome set)。对于每一个参与者 都有一个偏好函数( preference function)
都有一个偏好函数( preference function) .
.- 展开形式的博弈
- 展开形式的博弈又可译为扩展形式的博弈、扩展式赛局或扩展型赛局。正则形式的定义为数学家们提供了“均衡”(equilibria)问题的研究一个容易使用的表达式。因为它避免了怎么计算“策略”的问题,也就是说游戏是怎么进行的问题。若要考虑游戏是如何进行的,展开形式的博弈是一个比较方便的表达式。这个形式与组合博弈论关系密切。这个定义通过一个树的形式给定。在树的每一个节点(vertex),不同的参与者选择一个边(edge)。纳什均衡如果某情况下无一参与者可以独自行动而增加收益,则此策略组合被称为纳什均衡点。例子其经典的例子就是囚徒困境。囚徒困境是一个非零和博弈。 大意是:一个案子的两个嫌疑犯被分开审讯,警官分别告诉两个囚犯,如果你招供,而对方不招供,则你将被立即释放,而对方将被判刑十年;如果两人均招供,将均被判刑两年。如果两人均不招供,将最有利,只被判刑半年。 于是,两人同时陷入招供还是不招供的两难处境。 但两人无法沟通,于是从各自的利益角度出发,都依据各自的理性而选择了招供, 这种情况就称为纳氏均衡点。 这时,个体的理性利益选择是与整体的理性利益选择不一致的。
囚犯甲的博弈矩阵 囚犯甲 招供 不招供 囚犯乙 招供 各判刑两年 甲判刑十年,乙立即释放 不招供 甲立即释放,乙判刑十年 各判刑半年 基于经济学中“理性经济人”的前提假设,两个囚犯符合自己利益的选择是坦白招供,原本对双方都有利的策略不招供从而均被判刑半年就不会出现。事实上,这样两人都选择坦白的策略以及因此被判两年的结局被称作是“纳什均衡”(也叫非合作均衡),换言之,在此情况下,无一参与者可以“独自行动”(即单方面改变决定)而增加收获。
对称性与守恒的完美统一——诺特定理
诺特定理是理论物理的中心结果之一,它表达了连续对称性和守恒定律的一一对应。例如,物理定律不随着时间而改变,这表示它们有关于时间的某种对称性。如果我们想象一下,譬如重力的强度每天都有所改变,我们就会违反能量守恒定律,因为我们可以在重力弱的那天把重物举起,然后在重力强的时候放下来,这样就得到了比我们开始输入的能量更多的能量。
表述
解释
定理的形式化命题仅从不变性条件就导出和一个守恒的物理量相应的流的表达式。该守恒量称为诺特荷,而该流称为诺特流。诺特流至多相差一个无散度向量场。
应用
诺特定理的应用帮助物理学家在物理的任何一般理论中通过分析各种使得所涉及的定律的形式保持不变的变换而获得深刻的洞察力。例如:
证明
物理学中这样的"M"的例子包括:
- 经典力学上,哈密顿表述中,M是一个一维流形R,代表时间而目标空间是广义位置的空间的余切丛。
- 场论中,M是时空流形,而目标空间是场在任何给定可取的值的集合。例如,如果有m个实值标量场,φ1,...,φm,则目标流形是Rm。若流形是一个实向量场,则目标流形同构于R3。
现在设有一个泛函
要得到通常版本的诺特定理,我们需要对作用量作额外的限制。我们假设S[φ]是M上的如下函数的积分
其二是φ满足给定边界条件。(参看稳定作用量原理)
对于所有紧致子流形N成立,换句话讲(散度定理),
对于所有x成立,其中我们令![\mathcal{L}(x)=\mathcal{L}[\phi(x), \partial_\mu \phi(x),x]](http://upload.wikimedia.org/math/f/6/c/f6cf2354eecd50f484db2c72990779b8.png) 。
。
![\mathcal{L}(x)=\mathcal{L}[\phi(x), \partial_\mu \phi(x),x]](http://upload.wikimedia.org/math/f/6/c/f6cf2354eecd50f484db2c72990779b8.png) 。
。
因为这对于所有N成立,我们有
但这无非就是对于如下的流的连续性方程
这被称为和该对称性相关的诺特流(Noether current)。该连续性方程说明如果对这个流在空间式切片上积分,就可以得到称为诺特荷的守恒量(当然,必须假定M非紧致时,该流趋向无穷远处时下降足够快)。
评论
诺特定理实际上是边界条件和变分原理的关系的反映。假设作用量没有边界项,诺特定理意味着
假定我们有两个对称性求导Q1和Q2。则[Q1,Q2]也是一个对称性求导。显式德来看
及
其中f12=Q1[f2μ]-Q2[f1μ]。所以,
这表明我们可以(简单地)将诺特定理扩张到更大的李代数上。
证明的一般化
这个推理可以应用到任何求导过程Q,不只是对称性求导,也可以是更一般的泛函微分作用,包括拉格朗日量依赖于场的更高阶的导数以及非局部作用量的情况。令ε为任意时空(或时间)流形的光滑函数,满足其支撑的闭包和边界不交。ε是一个测试函数。则根据变分原理(附带说一下,它不适用于边界),由q[ε][φ(x)]=ε(x)Q[φ(x)]生成的求导分布q满足q[ε][S]=0对于任何在壳的ε成立,或者可以简写为q(x)[S]对于所有不在边界上的x(注意q(x)是求导分布的简写,通常不是用x参数化的求导)。这就是诺特定理的一般化。
要看出这个一般化和上面的版本如何对应,我们可以假设作用量就是只依赖于φ及其一阶导数的时空积分。并且,假设
(离壳或仅仅在壳都可以)。则,
对于所有ε成立。
更一般地讲,如果拉格朗日量依赖于高阶导数,则
![\partial_\mu\left[f^\mu-\left[\frac{\partial}{\partial (\partial_\mu\phi)}\mathcal{L}\right]Q[\phi]-2\left[\frac{\partial}{\partial (\partial_\mu \partial_\nu \phi)}\right]\partial_\nu Q[\phi]+\partial_\nu\left[\left[\frac{\partial}{\partial (\partial_\mu \partial_\nu \phi)}\mathcal{L}\right] Q[\phi]\right]-\,\cdots\right]=0.](http://upload.wikimedia.org/math/b/f/5/bf54e40fd9c3efa55bbec6f7d990967e.png)
- 例子
例1:能量守恒
我们来看一个特殊情况。假设有一个1维流形其拓扑结构为R (时间),坐标用t。设(也即,在一个弯曲黎曼空间(但不是弯曲时空)中运动的一个牛顿质点,该空间度量为g,质点势能为V)。取Q为时间平移的生成元。换句话说,![Q[x(t)]=\dot{x}(t)](http://upload.wikimedia.org/math/f/9/7/f974556db0dab99880bb67049ce3b681.png) 。 [量子场理论学家经常在方程右边加上一个因子i]。 注意这有如下形式所以我们可以置则,可以认出右边就是能量,而诺特定理就是说
。 [量子场理论学家经常在方程右边加上一个因子i]。 注意这有如下形式所以我们可以置则,可以认出右边就是能量,而诺特定理就是说 (也即,能量守恒就是时间平移的不变性的结果)。更一般的来讲,若拉格朗日量不显式依赖于时间,如下物理量(称为哈密顿量)是守恒的。例子2:线性动量守恒继续使用一维时间。这次,令也即N个势能只依赖于两两相对位移的牛顿质点。对于
(也即,能量守恒就是时间平移的不变性的结果)。更一般的来讲,若拉格朗日量不显式依赖于时间,如下物理量(称为哈密顿量)是守恒的。例子2:线性动量守恒继续使用一维时间。这次,令也即N个势能只依赖于两两相对位移的牛顿质点。对于 ,考虑平移变换的生成元(也即坐标系的变换)。换句话说,注意所以我们置则,
,考虑平移变换的生成元(也即坐标系的变换)。换句话说,注意所以我们置则,-

- 诺特定理表明
 (说明每个方向上的总动量守恒来自该方向上的平移不变性).
(说明每个方向上的总动量守恒来自该方向上的平移不变性).
美丽的扩展——辛空间
数学上,一个辛流形是一个装备了一个闭、非退化2-形式ω的光滑流形,ω称为辛形式。辛流形的研究称为辛拓扑。辛流形作为经典力学和分析力学的抽象表述中的流形的余切丛自然的出现,例如在经典力学的哈密顿表述中,该领域的一个主要原因之一:一个系统的所有组态的空间可以用一个流形建模,而该流形的余切丛描述了该系统的相空间。
一个辛流形上的任何实值可微函数H可以用作一个能量函数或者叫哈密顿量。和任何一个哈密顿量相关有一个哈密顿向量场;该哈密顿向量场的积分曲线是哈密顿-雅可比方程的解。哈密顿向量场定义了辛流形上的一个流场,称为哈密顿流场或者叫辛同胚。根据刘维尔定理,哈密顿流保持相空间的体积形式不变。
线性辛流形
有一个标准“局部”模型,也就是R2n,其中ωi,n+i = 1; ωn+i,i = -1; ωj,k = 0 对于所有 i = 0,...,n-1; j,k=0,...,2n-1 (k ≠ j+n and j ≠ k+n)。这是一个线性辛空间的例子。参看辛向量空间。一个称为达布定理的命题表明局部来看每个辛流形都和这个简单的辛流形相似
体积形式
切触流形
和辛流形紧密相关的有一个奇数维流形,称为切触流形。每个2n+1-维切触流形(M, α)给出一个2n+2-维辛流形(M × R, d(et α)).
拉格朗日子流形
辛流形的子流形有两个自然的几何概念,它们是辛子流形(可以是任何偶数维)和拉格朗日子流形(一半维度),其中辛流形要导出该子流形上的一个辛形式,而辛流形限制到拉格朗日子流形的切空间上时为0。拉格朗日子流形自然地出现在很多物理和几何的情况中;例如,辛同胚的图像在乘积辛流形(M × M, ω × −ω)上是拉格朗日子流形。
辛矢量空间
确切地说,一个辛形式是一个双线性形式 ω :V × V → R 满足:
- 斜对称:ω(u, v) = −ω(v, u),对所有 u, v ∈ V 成立;
- 非退化:如果 ω(u, v) = 0 对所有 v ∈ V 成立,那么 u = 0 。
非退化斜对称双线性形式和非退化“对称”双线性形式,比如欧几里得矢量空间的内积,的表现非常不同。欧几里得内积 g,对任何非零矢量 v,均有 g(v,v) > 0 成立;但是一个辛形式 ω 满足 ω(v,v) = 0 。
标准辛空间
这里 In 是 n × n 单位矩阵。用基矢量表示
 :
:

有另外一种方式理解标准辛形式。因上面所使用的带有标准结构的模型空间 Rn 容易导致误会,我们用一个“匿名”空间替代之。设 V 是一个 n-维实矢量空间,V∗ 为其对偶空间。现在考虑直和 W := V ⊕ V∗,带有如下形式:
选取 V 的任何一组基 (v1, …, vn) ,考虑其对偶基
我们能将基理解成在 W 中的矢量。若记 xi = (vi, 0) 和 yi = (0, vi∗),将它们放在一块,组成了 W 一组完整的基,
这里定义的形式  可以证明具有本节最初的那些性质,换句话说,每一个辛结构都同构于一个形如V ⊕ V∗的形式。
可以证明具有本节最初的那些性质,换句话说,每一个辛结构都同构于一个形如V ⊕ V∗的形式。
 可以证明具有本节最初的那些性质,换句话说,每一个辛结构都同构于一个形如V ⊕ V∗的形式。
可以证明具有本节最初的那些性质,换句话说,每一个辛结构都同构于一个形如V ⊕ V∗的形式。
对子空间V的选择不是唯一的,对V选择的过程称为极化. 给出了一个这样的同构的子空间称为一个拉格朗日子空间或简称拉氏子空间.
更加明确的说,给定一个拉氏子空间(如之前定义), 那么对基  的选择,通过性质
的选择,通过性质 决定了对应的一组对偶基.
决定了对应的一组对偶基.
 的选择,通过性质
的选择,通过性质 决定了对应的一组对偶基.
决定了对应的一组对偶基.
辛群
如果 V = W,则一个辛映射称为 V 上的线性辛变换。特别的,在这种情形我们有:
子空间
设 W 是 V 的一个线性子空间,定义 W 的辛补(空间)为子空间:
 对所有
对所有 
辛补满足
和
但是,不像正交补, W⊥ ∩ W 不一定为 {0}。我们讨论四种情形:
- W 是辛子空间,如果 W⊥ ∩ W = {0}。当且仅当 ω 在 W 上的限制是非退化时成立。带有限制形式的一个辛子空间本身也是一个辛矢量空间。
- W 是迷向子空间,如果 W ⊆ W⊥。当且仅当 ω 限制在 W 上为 0 时成立。任何 1-维子空间都是迷向的。
- W 是余迷向子空间,如果 W⊥ ⊆ W。 W 是余迷向的当且仅当ω 在商空间 W/W⊥ 上非退化。等价地 W 是余迷向的当且仅当 W⊥ 是迷向的。任何余维数为 1 的子空间都是余迷向的。
- W 是拉格朗日子空间,如果 W = W⊥。一个子空间是拉格朗日的当且仅当它既是迷向又是余迷向的。在有限维矢量空间,一个拉格朗日子空间是维数为 V 之一半的迷向子空间。任何迷向子空间可以扩充为一个拉格朗日子空间。
对上面的标准矢量空间 R2n,
- 由 {x1, y1} 生成的子空间是辛子空间;
- 由 {x1, x2} 生成的子空间是迷向子空间;
- 由 {x1, x2, …, xn, y1} 生成的子空间是余迷向子空间;
- 由 {x1, x2, …, xn} 生成的子空间是拉格朗日子空间。
几个非常优美的关于圆周率的公式
下面给出几个关于圆周率的公式(非弱智型),这几个公式的神奇之处在于它们和整数,素数,无限的结构有着深刻的联系。这也说明了圆周率不仅仅是一个几何意义的常数,而包含着数学中众多分支的精华。
1.这是韦达(Francois Viete,1540~1603)给出的史上第一个关于π的公式

注意到它的无穷的根式结构以及整个公式只用到了数字2!!!
2.沃利斯(John Wallis,1616~1703)π方程

毫无疑问这个公式非常漂亮,因为这是一个无穷乘积,形式上很简洁。沃利斯通过计算两个积分(这两个积分是正弦函数的2n+1次幂与2n-1次幂,从0积到π/2)得到两个关于n的分式,再用两边夹方法得到了这个公式。
3.这个公式是拉马努金发现的

整个公式充满了拉马努金的风格,他发挥自己在无穷级数与无穷连分式方面深刻的洞察力将两大数学常数完美地融合在了一起
4.斯特林(String)公式的变形

其实这个公式是斯特林公式变形,但好处在于,有极限,有指数,有阶乘,有e,有π。信息量相当大
5.貌似是一个当官的导出来的

貌似是外国一个伯爵看到了沃利斯公式,就将其化成了无穷连分式。虽是变形,可美感更深一层了。可以清晰地看到圆周率和奇数,平方数之间神秘的关系。
6.欧拉(Euler)发现的公式

欧拉是个巧匠,他运用各种巧妙而又简单的方法发现了大量美丽的公式和定理,以上便是一例。在这里,圆周率跟质数联系到了一起(注意,貌似应该是负一的n次方。)
7.高精度计算π的公式

高精度不是吹的,这个简单而又优美的公式居然不是π的精确公式,却可以将π精确到小数点后420亿位!!!纯造化~~~
1.这是韦达(Francois Viete,1540~1603)给出的史上第一个关于π的公式

注意到它的无穷的根式结构以及整个公式只用到了数字2!!!
2.沃利斯(John Wallis,1616~1703)π方程

毫无疑问这个公式非常漂亮,因为这是一个无穷乘积,形式上很简洁。沃利斯通过计算两个积分(这两个积分是正弦函数的2n+1次幂与2n-1次幂,从0积到π/2)得到两个关于n的分式,再用两边夹方法得到了这个公式。
3.这个公式是拉马努金发现的

整个公式充满了拉马努金的风格,他发挥自己在无穷级数与无穷连分式方面深刻的洞察力将两大数学常数完美地融合在了一起
4.斯特林(String)公式的变形

其实这个公式是斯特林公式变形,但好处在于,有极限,有指数,有阶乘,有e,有π。信息量相当大
5.貌似是一个当官的导出来的

貌似是外国一个伯爵看到了沃利斯公式,就将其化成了无穷连分式。虽是变形,可美感更深一层了。可以清晰地看到圆周率和奇数,平方数之间神秘的关系。
6.欧拉(Euler)发现的公式

欧拉是个巧匠,他运用各种巧妙而又简单的方法发现了大量美丽的公式和定理,以上便是一例。在这里,圆周率跟质数联系到了一起(注意,貌似应该是负一的n次方。)
7.高精度计算π的公式

高精度不是吹的,这个简单而又优美的公式居然不是π的精确公式,却可以将π精确到小数点后420亿位!!!纯造化~~~
天才数学家拉马努金(来自wikipedia)
拉马努金(泰米尔文:ஸ்ரீநிவாச ராமானுஜன்,拉丁字母转写:Srinivasa Aiyangar Ramanujan)(1887年12月22日-1920年4月26日),印度数学家。没受过正规的高等数学教育,沉迷数论,尤爱牵涉π、质数等数学常数的求和公式,以及整数分拆。惯以直觉(或者是跳步)导出公式,不喜作证明(事后往往证明他是对的)。他留下的那些没有证明的公式,引发了后来的大量研究。1997年,《拉马努金期刊》(Ramanujan Journal)创刊,用以发表有关“受到拉马努金影响的数学领域”的研究论文。
在11岁时,他已经掌握了住在他家的房客的数学知识,他们是政府大学的学生,到13岁,他就掌握了借来的高等三角学的书里的知识。他的传记作家称他的天才在14岁时开始显露。他不仅在他的学生岁月里不断获得荣誉证书和奖学金,他还帮学校处理把1200个学生(各有不同需要)分配给35个教师的后勤事务,他甚至在一半的给定时间内完成测验,还已经显示出对无穷级数的熟练掌握;他那时的同校的人后来回忆说:“我们,包括老师,很少可以理解他,并对他‘敬而远之’”。但是,拉马努金在其他科目无法集中注意力,并在高中考试中不合格。在他生活的这个时段,他也相当穷困,经常到了挨饿的地步。




哈代这样评论拉马努金:
在11岁时,他已经掌握了住在他家的房客的数学知识,他们是政府大学的学生,到13岁,他就掌握了借来的高等三角学的书里的知识。他的传记作家称他的天才在14岁时开始显露。他不仅在他的学生岁月里不断获得荣誉证书和奖学金,他还帮学校处理把1200个学生(各有不同需要)分配给35个教师的后勤事务,他甚至在一半的给定时间内完成测验,还已经显示出对无穷级数的熟练掌握;他那时的同校的人后来回忆说:“我们,包括老师,很少可以理解他,并对他‘敬而远之’”。但是,拉马努金在其他科目无法集中注意力,并在高中考试中不合格。在他生活的这个时段,他也相当穷困,经常到了挨饿的地步。
在1913年拉马努金发了一长串复杂的定理给三个剑桥的学术界人士贝克(H. F. Baker)、霍布森(E. W. Hobson)、哈代(G. H. Hardy),只有三一学院的院士哈代注意到了拉马努金定理中所展示的天才。
读着不知名和未经训练的印度数学家的突然来信,哈代和他的同事利特尔伍德(J.E. Littlewood)评论道:“没有一个定理可以放到世界上最高等的数学测试中。”虽然哈代是当时著名的数学家而且是拉马努金所写的其中几个领域中的专家,他还是说很多定理:“完全打败了我”、“我从没见过任何像这样的东西。”
作为他的成果的一个例子,拉马努金给出了漂亮的连分数:

其中fai是黄金分割比
在数学上,有洞察力和有一个证明是很不相同的。拉马努金的天才给出了大量的公式,可以再深入研究,开启了新的研究方向。这些公式的例子有圆周率的一些引人入胜的无穷级数,其中一个是:

这和如下事实相关:

他提出对所有 θ

此处Γ(z)代表伽傌函数。
比较恒等式两边θ之不同幂的系数,就可以得出双曲正割的许多恒等式。
哈代这样评论拉马努金:
| 他的知识的缺陷和它的深刻一样令人吃惊。这是一个能够发现模方程和定理的人……直到前所未闻的地步,他对连分数的掌握……超出了世界上任何一个数学家,他自己发现了ζ函数的泛函方程和解析数论中的很多著名问题的主导项;但他却没有听说过双周期函数或者柯西定理,对复变函数只有最模糊的概念…… |
盯着结论看,直到它变得显然成立为止 (转自MATRIX67)
很多看上去很显然的结论,其实是需要严格证明的,并且有时候证明相当困难。比方说算术基本定理,每一个数分解质因数的方法都是唯一的。这看上去几乎是显然的,但证明过程需要很多深刻的数论知识。更极端的例子则是 Jordan 曲线定理,即平面上每一条不与自身相交的封闭曲线都把平面分成了里外两部分。这几乎就是一句废话,但要想严格证明起来相当不容易, Camille Jordan 本人的证明最后发现竟然也是错误的。
最近 MathOverflow上有人提了一个非常有趣的问题:有那么多结论很显然但证明很困难的定理,那有没有什么结论很不可思议但证明过程却不言而喻的定理呢?
最近 MathOverflow上有人提了一个非常有趣的问题:有那么多结论很显然但证明很困难的定理,那有没有什么结论很不可思议但证明过程却不言而喻的定理呢?
在众人的回答中,呼声最高的就是 Desargues 定理:若三角形 ABC 和 A'B'C' 中, AA' 、 BB' 、 CC' 所在直线交于一点,则两个三角形中每一组对应边的交点(即 BC 和 B'C' 的交点 D 、 AC 和 A'C' 的交点 E 、 AB 和 A'B' 的交点 F )是共线的。
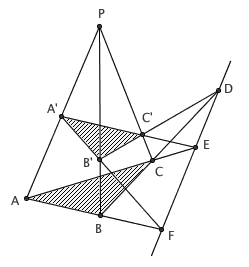
这个定理看上去太神奇了,大家一定会以为证明很难吧。但事实上,这个定理根本不需要证明,它显然是成立的。现在,把 P-ABC 看成一个三棱锥,而 A'B'C' 则是一个不平行于底面的截面。由于 AB 、 A'B' 在同一平面内,因此这两条线会相交;这个交点既在平面 ABC 上,也在平面 A'B'C' 上,因而也就在两平面的交线上。同理,另外两个交点也都在平面 ABC 和 A'B'C' 的交线上,因此三个交点共线。当然,画在纸上的也好,照相机照出来的也好,人眼看到的也好,其实都是一个二维图形罢了。因此,命题在平面上也是成立的(这背后的逻辑是,在立体图形的平面投影中,直线仍然是直的,共线的仍然共线,共点的仍然共点;借助射影几何的思想,我们能给出一个更严格的证明)。
这个证明神就神在,当你悟到之后,整个证明过程不但不需要一个字,而且连图形说明都可以不用,只需要盯着原图看,结论自己就跳出来了。看来,我们又多了一种证明问题的思路:盯着问题看,直到它突然一下变得显然成立了为止。
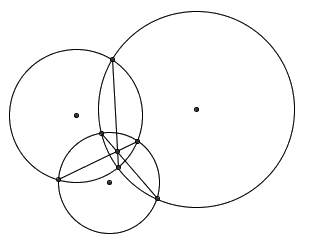
问题很帅:平面上三个圆两两相交。试证明三条公共弦共点。

利用根轴的相关性质,我们有一个非常漂亮的证明。不过,要想看出定理的正确性,远不用那么复杂。用一种新的方式解读原图后,定理几乎是显然成立的。想象以这三个圆为“赤道面”的三个球体。我们把这三个球的球心(也就是原问题中的三个圆心)所确定的平面(也就是原问题的图形所在的平面)记作 α 。注意到,每两个球面将会相交于一个圆圈,他们在 α 上的投影就是那三条公共弦。而三个球面将会交于两个点(这两个点一上一下,关于 α 对称),并且这两个点都同时属于空间中的三个圆圈。从投影的角度来看,这就是说,在平面 α 上存在一个点,它同时属于那三条公共弦。
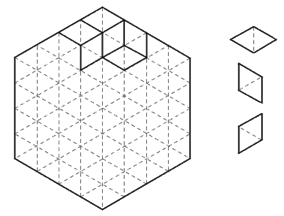
说到直观的证明,不得不提到下面这个经典例子。 1989 年的 American Mathematical Monthly 上有一个貌似非常困难的数学问题:考虑由一个个小三角形组成的正六边形棋盘,现在请你用右边的三种(仅朝向不同的)菱形把整个棋盘全部摆满(图中只摆了其中一部分),证明当你摆满整个棋盘后,你所使用的每种菱形数量一定相同。
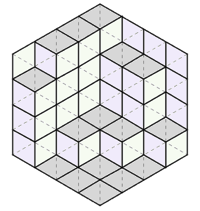
文章末尾提供了一个非常帅的“证明”。把每种菱形涂上一种颜色,整个图形瞬间有了立体感,看上去就成了一个个立方体在墙角堆叠起来的样子。三种菱形分别是从左侧、右侧、上方观察整个立体图形能够看到的面,它们的数目显然应该相等。这个证明虽然并不严格,但却深受数学家喜爱,甚至还收录进了《Proofs Without Words》一书中。
《Proofs Without Words》一书的第 109 页则给出了另外一个例子:六边形数 hn 可以写成 n3 - (n - 1)3 。其实这也是显然的,结论根本不用证明。你只需要盯着排列成六边形的圆点阵,不断看不断看,一直看一直看,直到看出它显然就是 n3 - (n - 1)3 ,结论就证到了。
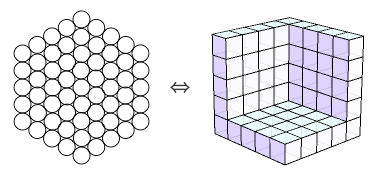
由此还能立刻可知, h1 + h2 + … + hn = n3 ,从图形的角度看上去,这也是显然的。
大家还有什么好的例子吗?
Trackback: http://www.matrix67.com/blog/archives/4480/trackback


































































































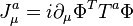









 代表
代表

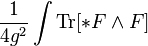

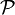 表示路径排序算子。(From Wikipedia)
表示路径排序算子。(From Wikipedia)
 定义如下:
定义如下: 未必能提升至李群的映射
未必能提升至李群的映射  ,但可提升至映射
,但可提升至映射  ,其中
,其中  是
是  的万有
的万有

 ;至于数论方面,特别涉及
;至于数论方面,特别涉及
 中的离散加法子群,使得其商群
中的离散加法子群,使得其商群 的截面。模形式的情形也类似,但考虑的不是
的截面。模形式的情形也类似,但考虑的不是  0)">。对一模形式
0)">。对一模形式  。模形式的第二个条件可改写成函数方程:对所有
。模形式的第二个条件可改写成函数方程:对所有 且
且  (即
(即 之定义),有
之定义),有



 ,则称之为
,则称之为 的最小
的最小 
 中的偶
中的偶 ,是指由一个
,是指由一个

 对这两个格的商空间给出两个 16 维环面,彼此不相
对这两个格的商空间给出两个 16 维环面,彼此不相
 是权
是权  的模形式。
的模形式。 的傅立叶展开式中,对任一素数
的傅立叶展开式中,对任一素数  的系数的绝对值恒
的系数的绝对值恒  。此猜想最后由
。此猜想最后由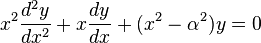

 必须为0时,才能获得有物理意义的结果。
必须为0时,才能获得有物理意义的结果。




 型
型

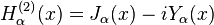
 。以上的线性组合也成为第三类贝塞尔函数;它们描述了二维
。以上的线性组合也成为第三类贝塞尔函数;它们描述了二维

















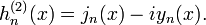




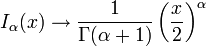





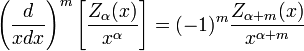

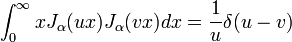














 以及其
以及其 。使用
。使用

 (称为
(称为 ,
, 为任何实数,定义一个新的联络
为任何实数,定义一个新的联络


 为阿希提卡-巴贝罗联络定义的
为阿希提卡-巴贝罗联络定义的 为阿希提卡-巴贝罗联络定义的
为阿希提卡-巴贝罗联络定义的




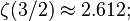 (
(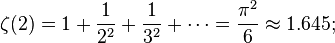 (
(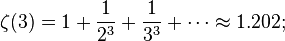 (
(
 是一个“参与者”(players)的集合。对于每一个“参与者”
是一个“参与者”(players)的集合。对于每一个“参与者” . 博弈(游戏)是一个
. 博弈(游戏)是一个
 为从M到T的
为从M到T的
 中而非
中而非 中取值;这是有物理原因的,并且并不影响本证明。)
中取值;这是有物理原因的,并且并不影响本证明。)
![S[\varphi]\equiv\int_M d^nx \mathcal{L}[\varphi(x),\partial_\mu\varphi(x),x].](http://upload.wikimedia.org/math/9/2/a/92a8f9638585e577dcd78833618e69bd.png)
![\frac{\delta}{\delta \phi(x)}S[\phi]=0](http://upload.wikimedia.org/math/f/5/e/f5ea4995e008bf79f9bb122278dbbb64.png)
![Q\left[\int_N d^nx\mathcal{L}\right]=\int_{\partial N}ds_\mu f^\mu[\phi(x),\partial\phi,\partial\partial\phi,...]](http://upload.wikimedia.org/math/1/b/0/1b03d16c1105e239dda6cc7049ca216c.png)
![Q[\mathcal{L}(x)]=\partial_\mu f^\mu(x)](http://upload.wikimedia.org/math/b/1/1/b111fc1897dd8f9005f0bae86620429d.png)
![Q\left[\int_Nd^nx\mathcal{L}\right]](http://upload.wikimedia.org/math/c/1/a/c1a17f6e910a3f4d4b0350fb7840f704.png)

![Q_1[\mathcal{L}]=\partial_\mu f_1^\mu](http://upload.wikimedia.org/math/4/6/1/461751f05d1cc026beba630d60e7707f.png)
![Q_2[\mathcal{L}]=\partial_\mu f_2^\mu](http://upload.wikimedia.org/math/8/9/9/89920be675101486c5690b943dc19033.png)
![[Q_1,Q_2][\mathcal{L}]=Q_1[Q_2[\mathcal{L}]]-Q_2[Q_1[\mathcal{L}]]=\partial_\mu f_{12}^\mu](http://upload.wikimedia.org/math/1/b/c/1bca2fd14657ef892000d70f06de2604.png)
![j_{12}^\mu=\left(\frac{\partial}{\partial (\partial_\mu\phi)}\mathcal{L}\right)(Q_1[Q_2[\phi]]-Q_2[Q_1[\phi]])-f_{12}^\mu.](http://upload.wikimedia.org/math/4/4/c/44cb4b9c7a020ef7a37470a7796ac4f5.png)
![Q[\mathcal{L}]=\partial_\mu f^\mu](http://upload.wikimedia.org/math/4/9/5/49540abb169b813a1ddfc5ec5397b303.png)
![q[\epsilon][S]=\int d^dx q[\epsilon][\mathcal{L}]](http://upload.wikimedia.org/math/7/f/3/7f378bc1077ab52b4156e6750fd6d900.png)
![=\int d^dx \epsilon \partial_\mu \Bigg\{f^\mu-\left[\frac{\partial}{\partial (\partial_\mu\phi)}\mathcal{L}\right]Q[\phi]\Bigg\}](http://upload.wikimedia.org/math/8/2/4/824b9c339d250e3e9c513d840e93ed86.png)
![S[x]\,](http://upload.wikimedia.org/math/1/8/a/18ac05fe094f54a001f095768810e2ff.png)
![=\int dt \mathcal{L}[x(t),\dot{x}(t)]](http://upload.wikimedia.org/math/9/b/b/9bb6ccfc272047203048dbc0dc10ec3c.png)
![=\int dt \left\{\frac{m}{2}g_{ij}\dot{x}^i(t)\dot{x}^j(t)-V[x(t)]\right\}](http://upload.wikimedia.org/math/c/d/0/cd08180e8ee8c6a8ceec331befc358a1.png)
![Q[\mathcal{L}]=m g_{ij}\dot{x}^i\ddot{x}^j-\frac{\partial}{\partial x^i}V(x)\dot{x}^i.](http://upload.wikimedia.org/math/5/e/9/5e92baee6f02b30d556a4b8fd6485570.png)
![\frac{d}{dt}\left[\frac{m}{2} g_{ij}\dot{x}^i\dot{x}^j-V(x)\right]](http://upload.wikimedia.org/math/b/8/3/b839b97f3ef02026dda6cdf8641c02cc.png)

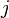
![=m g_{ij}\dot{x}^j\dot{x}^i-\left[\frac{m}{2} g_{ij}\dot{x}^i\dot{x}^j-V(x)\right]](http://upload.wikimedia.org/math/0/d/1/0d132b4e32e61d9754cdc07660be66f9.png)


![S[\vec{x}]\,](http://upload.wikimedia.org/math/2/7/b/27babdea2c39feac8409870b2c0470db.png)
![=\int dt \mathcal{L}[\vec{x}(t),\dot{\vec{x}}(t)]](http://upload.wikimedia.org/math/6/d/9/6d9c0815a27f102117c29f199ea6329b.png)
![=\int dt \left [\sum^N_{\alpha=1} \frac{m_\alpha}{2}(\dot{\vec{x}}_\alpha)^2 -\sum_{\alpha<\beta} V_{\alpha\beta}(\vec{x}_\beta-\vec{x}_\alpha)\right]](http://upload.wikimedia.org/math/7/9/1/7916d18aa27ccd58b0790ba536ba8bb8.png)
![Q_i[x^j_\alpha(t)]= \delta^j_i.](http://upload.wikimedia.org/math/9/e/0/9e09cf5e96b3403c17fc03f3f38eccc0.png)
![Q_i[\mathcal{L}]=0](http://upload.wikimedia.org/math/e/9/6/e96bb5dd26799ef3cc3ca201f7eb8728.png)

![\vec{J_i}=\sum_\alpha \left(\frac{\partial}{\partial \dot{\vec{x}}_\alpha}\mathcal{L}\right)\cdot\vec{Q}[\vec{x}_\alpha]-\vec{f}](http://upload.wikimedia.org/math/9/1/2/9122f14e12cbd265483612686afa9431.png)







 (详细的说法是可列可加的正测度)是个函数。设
(详细的说法是可列可加的正测度)是个函数。设 是集合
是集合 上的一个
上的一个 中取值,并且满足以下性质:
中取值,并且满足以下性质: 。
。 可加性:若
可加性:若 为
为 的
的 。
。 称为一个测度空间,而
称为一个测度空间,而 为可测集(不必是两两不交的),则集合
为可测集(不必是两两不交的),则集合 的并集是可测的,且有如下不等式(“
的并集是可测的,且有如下不等式(“
 ,
, ,则如下
,则如下

 ,令
,令
 。
。 中的盒子是形如
中的盒子是形如![B=\prod_{i=1}^n [a_i,b_i]](http://upload.wikimedia.org/wikipedia/zh/math/5/0/e/50e5bfd0c4a1e22caa1dcc727ac9885c.png) 的集合,其中
的集合,其中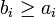 。这个盒子的体积
。这个盒子的体积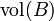 定义为
定义为
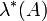 :
: 是可数个盒子的集合,它的并集覆盖了
是可数个盒子的集合,它的并集覆盖了
 ,都有:
,都有: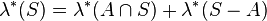
















No comments:
Post a Comment