Wednesday, February 19, 2014

有限元 将一个连续区域转化为一族离散的有限个三角形的子区域

有限元分析[编辑]
维基百科，自由的百科全书
（重定向自有限元方法）
跳转至： 导航、 搜索
本條目存在如下問題，請協助改善本條目或在討論頁針對議題發表看法。
本条目離題。
掛模板者須於討論頁闡明文章離題之處以便其他編者討論及修改。請參閱討論頁的意見。
本条目需要精通或熟悉本主题的编者参与及协助编辑。
請邀請適合的人士改善这篇条目。更多的細節與詳情請參见條目討論頁。您可以关注您所擅长领域的专家关注分类。
有限元分析，即有限元方法（冯康首次发现时称为基于变分原理的差分方法），是一种用于求解微分方程组或积分方程组数值解的数值技术. 这一解法基于完全消除微分方程, 即将微分方程转化为代数方程组(稳定情形); 或将偏微分方程(组)改写为常微分方程(组)的逼近, 这样可以用标准的数值技术(例如欧拉法,龙格－库塔法等)求解.
在解偏微分方程的过程中, 主要的难点是如何构造一个方程来逼近原本研究的方程, 并且该过程还需要保持数值稳定性.目前有许多处理的方法， 他们各有利弊. 当区域改变时(就像一个边界可变的固体), 当需要的精确度在整个区域上变化, 或者当解缺少光滑性时, 有限元方法是在复杂区域(像汽车和输油管道)上解偏微分方程的一个很好的选择. 例如, 在正面碰撞仿真时, 有可能在"重要"区域(例如汽车的前部)增加预先设定的精确度并在车辆的末尾减少精度(如此可以减少仿真所需消耗); 另一个例子是模拟地球的气候模式, 预先设定陆地部分的精确度高于广阔海洋部分的精确度是非常重要的.


历史[编辑]

有限元法最初起源于土木工程和航空工程中的弹性和结构分析问题的研究. 它的发展可以追溯到Alexander Hrennikoff(1941)和Richard Courant(1942)的工作. 这些先驱者使用的方法具有很大的差异, 但是他们具有共同的本质特征: 利用网格离散化将一个连续区域转化为一族离散的子区域, 通常叫做元.Hrennikoff 的工作离散用类似于格子的网格离散区域; Courant 的方法将区域分解为有限个三角形的子区域, 用于求解来源于圆柱体转矩问题的二阶橢圓偏微分方程. Courant 的贡献推动了有限元的发展, 绘制了早期偏微分方程的研究结果.
有限元方法的发展开始于五十年代中后期使用在机身框架和结构分析上，并于六十年代通过斯图加特大学的en:John Argyris和柏克萊加州大學的en:Ray W. Clough在土木工程中的应用工作中积累经验。
1965年，冯康将其成果发表成论文。[1][2]

技术讨论[编辑]

以下用有限元分析解决两个简单问题, 更一般的问题可以类似的推导出来. 现假设读者已经熟悉微积分和线性代数.
P1 是一个较简单的一维问题
{\mbox{ P1 }}:{\begin{cases}u''(x)=f(x){\mbox{ in }}(0,1),\\u(0)=u(1)=0,\end{cases}}
其中f是已知函数, u是关于x的未知函数, u''是u对x的二阶导数.
二维比较简单的问题是狄利克雷问题
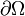{\mbox{P2 }}:{\begin{cases}u_{{xx}}(x,y)+u_{{yy}}(x,y)=f(x,y)&{\mbox{ in }}\Omega ,\\u=0&{\mbox{ on }}\partial \Omega ,\end{cases}}
其中\Omega 是 (x,y) 平面上的连通开区域, 它的边界 \partial \Omega 是良性的(例如, 光滑流形或多边形), u_{{xx}} 和 u_{{yy}} 分别表示 x 和 y 的二阶导数.问题 P1 能够通过计算不定积分而直接解决. 然而, 解决边值问题的这一方法只有在空间维数为1时才可用, 并且不能推广到高维问题以及形如 u+u''=f 的问题. 出于这种考虑,我们将用有限元方法解决 P1 并将其推广至问题 P2.
我们的描述分为两步, 每步都反映了用有限元解决边值问题的本质.
  • 将原问题描述为它的弱形式, 或变分形式. 这一步很少或不需要计算.
  • 离散化, 将弱形式在有限维空间离散化.
这两步之后, 我们可以构造一个大型有限维线性方程, 线性方程的解就是原边值问题的逼近解. 然后, 这一有限维问题由计算机求解.

变分形式[编辑]

第一步是将问题 P1 和 P2 转化为他的等价变分形式, 或弱解形式. 如果 u 是问题 P1 的解, 那么对任何满足边界条件的光滑函数 v , 有
(1) \int _{0}^{1}f(x)v(x)\,{\mathrm {d}}x=\int _{0}^{1}u''(x)v(x)\,{\mathrm {d}}x.
相反如果 u 对任何光滑函数 v(x) 满足 v(0)=v(1)=0 和 (1) 那么 u 是P1的解. 对于二次可导函数 u 证明这一点是非常容易的(利用中值定理).
通过对 (1) 的右侧使用分部积分, 可以得到
(2){\begin{aligned}\int _{0}^{1}f(x)v(x)\,{\mathrm {d}}x&=\int _{0}^{1}u''(x)v(x)\,{\mathrm {d}}x\\&=u'(x)v(x)|_{0}^{1}-\int _{0}^{1}u'(x)v'(x)\,{\mathrm {d}}x\\&=-\int _{0}^{1}u'(x)v'(x)\,{\mathrm {d}}x=-\phi (u,v).\end{aligned}}
其中使用了 v(0)=v(1)=0 的假设.

参考文献[编辑]

  1. ^ 冯, 康. 基于变分原理的差分格式. 应用数学与计算数学. 1965. 
  2. ^ http://www.amss.cas.cn/wh/cxwk/200908/t20090807_2352477.html
Posted by at

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)