搜尋結果
用正弦函数调制位势图显示平面矢量磁场的英文翻译_英语怎么说_海 ...
海词词典,最权威的学习词典,专业出版用正弦函数调制位势图显示平面矢量磁场的英文,用正弦函数调制位势图显示平面矢量磁场翻译,用正弦函数调制位势图显示 ...[PDF]
用正弦函数调制位势图显示平面矢量磁场
新的灰度纹理图像显示法。该方法用正弦函数对平面磁场的. 位势函数进行调制,从而将磁场矢量的信息映射为纹理图像. 的灰度值。这种新型纹理图像表现了磁通量管 ...[PDF]
篇名sin 勢顯2 函數sin( ) sin( ) y mx nx = + 疊合的極值問題作者李致廷 ...
www.shs.edu.tw/works/essay/2009/11/2009111511434231.pdf
在一年級下學期學到了三角函數,發現三角函數的圖形會進行有規律的變化,週期也會因 sin( ) y mx. = ... 因此我們就想看看,兩個正弦函數疊合,. 改變 sin( ) sin( ).
有限深方形阱- 维基百科,自由的百科全书
zh.wikipedia.org/zh-hk/有限深方形阱
在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函數 \psi \,\! 也不同,標記為:. \psi =\psi ... 是正弦函數與餘弦函數的線性組合:. \psi _{2}=A\sin(kx)+B\ ;.
正弦函数调制位势图的翻译结果 --cnki翻译助手
dict.cnki.net/h_3550990000.html - 轉為繁體網頁正弦函数调制位势图的翻译结果:sinusoidal function modulated potential maps||双语例句|英文例句|相关文摘. [PPT]
14_6一维无限深势阱中的粒子的波函数.ppt
如图所示,有一质量为m的粒子在一维势阱中运动,势函数为. 由于曲线像“井”且 ... 由于势阱无限高,粒子不能运动到势阱之外,所以定态波函数ψ(x) = 0 (x > a,x < 0)。 粒子在阱内定戊 ... 一维无限深势阱中粒子的波函数是正弦函数。 在两壁处,波函数 ...
1.3 量子力学的简单应用 - 结构化学章节内容
图1-6 一维势箱内自由粒子的波函数(左)和几率分布函数(右). 讨论:势箱中自由粒子的波函数是正弦函数,基态时,长度 势箱中只包含正弦函数半个周期,随着能级升 ...[PDF]
三角學的歷史對任意角三角函數的教學啟示 - 中研院數學研究所
w3.math.sinica.edu.tw/math_media/d363/36310.pdf
銳角三角函數是採用“三角比”來定義的, 這正是初高中三角函數知識的銜接點。 高. 中討論的 .... 知值出發, 推出了60◦ 的各倍分角的正弦函數值, 直到3.75◦。 值得一提的 ...
有限深方形阱[编辑]
在量子力學裏,有限深方形阱,又稱為有限深位勢阱,是無限深方形阱的延伸。有限深方形阱是一個阱內位勢為 0 ,阱外位勢為有限值的位勢阱。關於一個或多個粒子,在這種位勢作用中的量子行為的問題,稱為有限深位勢阱問題。與無限深方形阱問題不同的是,在阱外找到粒子的機率大於 0 。
在經典力學裏,假若,粒子的能量小於阱壁的位勢,則粒子只能移動於阱內,無法存在於阱外。截然不同地,在量子力學裏,雖然粒子的能量小於阱壁的位勢,在阱外找到粒子的機率大於 0 。
 ,左邊阱壁與右邊阱壁的位置分別為
,左邊阱壁與右邊阱壁的位置分別為  與
與  。阱內位勢為 0 。在阱壁,位勢突然升高為
。阱內位勢為 0 。在阱壁,位勢突然升高為  。阱外位勢保持為
。阱外位勢保持為  。這一維阱將整個一維空間分為三個區域:阱左邊,阱內,與阱右邊。在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函數
。這一維阱將整個一維空間分為三個區域:阱左邊,阱內,與阱右邊。在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函數 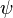 也不同,標記為:
也不同,標記為:
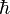 是約化普朗克常數,
是約化普朗克常數,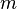 是粒子質量,
是粒子質量, 是粒子位置,
是粒子位置, 是位勢,
是位勢,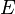 是能量。
是能量。
 ,方程簡化為:
,方程簡化為:
 為
為
 是正弦函數與餘弦函數的線性組合:
是正弦函數與餘弦函數的線性組合:
 與
與  都是複值常數,由邊界條件而決定。
都是複值常數,由邊界條件而決定。
 ,薛丁格方程為:
,薛丁格方程為:
 ,則這粒子束縛於位勢阱內.稱這粒子的量子態為束縛態(bound state)。設定
,則這粒子束縛於位勢阱內.稱這粒子的量子態為束縛態(bound state)。設定
 ,
,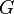 ,
, ,
, 都是常數。
都是常數。
從正確的邊界條件,可以找到常數 ,
, ,
, ,
,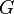 ,
, ,
, 的值。
的值。
總結前面導引出的結果,波函數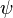 的形式為:
的形式為:
 趨向負無窮,包含
趨向負無窮,包含  的項目趨向無窮。類似地,當
的項目趨向無窮。類似地,當  趨向無窮,包含
趨向無窮,包含  的項目趨向無窮。可是,波函數在任何
的項目趨向無窮。可是,波函數在任何  都必須是有限值。因此,必須設定
都必須是有限值。因此,必須設定  。阱外區域的波函數變為
。阱外區域的波函數變為
 越小,波函數
越小,波函數  呈指數遞減。而在阱右邊,隨著
呈指數遞減。而在阱右邊,隨著  越大,波函數
越大,波函數  呈指數遞減。這是合理的。這樣,波函數才能夠歸一化。
呈指數遞減。這是合理的。這樣,波函數才能夠歸一化。
由於有限深方形阱對稱於 ,可以利用這對稱性來省略計算步驟。波函數不是奇函數就是偶函數。
,可以利用這對稱性來省略計算步驟。波函數不是奇函數就是偶函數。
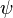 是奇函數,則
是奇函數,則
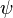 必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
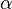 與波數
與波數  的關係:
的關係:
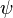 是偶函數,則
是偶函數,則
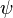 必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
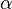 與波數
與波數  的關係:
的關係:
 ,則這粒子不會被束縛於位勢阱內。因此,在這裏,粒子的量子行為主要是由位勢阱造成的散射(scattering)行為。稱這粒子的量子態為散射態。稱這不被束縛的粒子為自由粒子。更強版的定義還要求位勢為常數。假若,一維空間分為幾個區域,只有在每個區域內,位勢為常數;而在區域與區域之間,位勢不相等,則稱此粒子為半自由粒子。自由粒子和半自由粒子的能量大於位勢,
,則這粒子不會被束縛於位勢阱內。因此,在這裏,粒子的量子行為主要是由位勢阱造成的散射(scattering)行為。稱這粒子的量子態為散射態。稱這不被束縛的粒子為自由粒子。更強版的定義還要求位勢為常數。假若,一維空間分為幾個區域,只有在每個區域內,位勢為常數;而在區域與區域之間,位勢不相等,則稱此粒子為半自由粒子。自由粒子和半自由粒子的能量大於位勢, ,不會被束縛於位勢阱內,能量不是離散能量譜的特殊值,而是大於或等於
,不會被束縛於位勢阱內,能量不是離散能量譜的特殊值,而是大於或等於  的任意值。波數
的任意值。波數 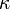 ,用方程式表達為
,用方程式表達為  ,也不是離散量。代入方程 (1) :
,也不是離散量。代入方程 (1) :
 、
、 、
、 、
、 ,都是常數。
,都是常數。
维基百科,自由的百科全书
在經典力學裏,假若,粒子的能量小於阱壁的位勢,則粒子只能移動於阱內,無法存在於阱外。截然不同地,在量子力學裏,雖然粒子的能量小於阱壁的位勢,在阱外找到粒子的機率大於 0 。
一維阱定義[编辑]
一維有限深方形阱的阱寬為 ,左邊阱壁與右邊阱壁的位置分別為
,左邊阱壁與右邊阱壁的位置分別為  與
與  。阱內位勢為 0 。在阱壁,位勢突然升高為
。阱內位勢為 0 。在阱壁,位勢突然升高為  。阱外位勢保持為
。阱外位勢保持為  。這一維阱將整個一維空間分為三個區域:阱左邊,阱內,與阱右邊。在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函數
。這一維阱將整個一維空間分為三個區域:阱左邊,阱內,與阱右邊。在每一個區域內,對應著不同的位勢,描述粒子的量子行為的波函數 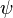 也不同,標記為:
也不同,標記為: :阱左邊,
:阱左邊,  (阱外區域),
(阱外區域), :阱內,
:阱內,  (阱內區域),
(阱內區域), :阱右邊,
:阱右邊, (阱外區域)。
(阱外區域)。
 ;(1)
;(1)
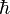 是約化普朗克常數,
是約化普朗克常數,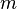 是粒子質量,
是粒子質量, 是粒子位置,
是粒子位置, 是位勢,
是位勢,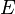 是能量。
是能量。阱內區域[编辑]
在阱內,位勢 ,方程簡化為:
,方程簡化為: 。(2)
。(2)
 為
為 。(3)
。(3)
 。
。
 是正弦函數與餘弦函數的線性組合:
是正弦函數與餘弦函數的線性組合: ;
;
 與
與  都是複值常數,由邊界條件而決定。
都是複值常數,由邊界條件而決定。阱外區域[编辑]
在阱外,位勢 ,薛丁格方程為:
,薛丁格方程為: 。
。
束縛態[编辑]
假若,粒子的能量小於位勢: ,則這粒子束縛於位勢阱內.稱這粒子的量子態為束縛態(bound state)。設定
,則這粒子束縛於位勢阱內.稱這粒子的量子態為束縛態(bound state)。設定 。(4)
。(4)
 。
。
 ,
, ;
;
 ,
,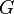 ,
, ,
, 都是常數。
都是常數。從正確的邊界條件,可以找到常數
 ,
, ,
, ,
,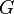 ,
, ,
, 的值。
的值。束縛態的波函數[编辑]
薛丁格方程的解答必須具有連續性與連續可微性。這些要求是前面導引出的微分方程的邊界條件。總結前面導引出的結果,波函數
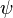 的形式為:
的形式為: :阱左邊,
:阱左邊,  (阱外區域),
(阱外區域), :阱內,
:阱內,  (阱內區域),
(阱內區域), :阱右邊,
:阱右邊, (阱外區域)。
(阱外區域)。
 趨向負無窮,包含
趨向負無窮,包含  的項目趨向無窮。類似地,當
的項目趨向無窮。類似地,當  趨向無窮,包含
趨向無窮,包含  的項目趨向無窮。可是,波函數在任何
的項目趨向無窮。可是,波函數在任何  都必須是有限值。因此,必須設定
都必須是有限值。因此,必須設定  。阱外區域的波函數變為
。阱外區域的波函數變為 ,
, 。
。
 越小,波函數
越小,波函數  呈指數遞減。而在阱右邊,隨著
呈指數遞減。而在阱右邊,隨著  越大,波函數
越大,波函數  呈指數遞減。這是合理的。這樣,波函數才能夠歸一化。
呈指數遞減。這是合理的。這樣,波函數才能夠歸一化。由於有限深方形阱對稱於
 ,可以利用這對稱性來省略計算步驟。波函數不是奇函數就是偶函數。
,可以利用這對稱性來省略計算步驟。波函數不是奇函數就是偶函數。奇的波函數[编辑]
假若,波函數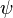 是奇函數,則
是奇函數,則 ,
, ,
, ,
,
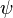 必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配: ,(5)
,(5) 。(6)
。(6)
 。
。
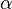 與波數
與波數  的關係:
的關係: 。
。
 。
。
偶的波函數[编辑]
假若,波函數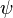 是偶函數,則
是偶函數,則 ,
, ,
, ,
,
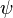 必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配:
必須滿足連續性與連續可微性。在阱壁,兩個波函數的函數值與導數值都必須相配: ,(7)
,(7) 。(8)
。(8)
 。
。
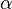 與波數
與波數  的關係:
的關係: 。
。
 。
。
散射態[编辑]
假若,一個粒子的能量大於位勢, ,則這粒子不會被束縛於位勢阱內。因此,在這裏,粒子的量子行為主要是由位勢阱造成的散射(scattering)行為。稱這粒子的量子態為散射態。稱這不被束縛的粒子為自由粒子。更強版的定義還要求位勢為常數。假若,一維空間分為幾個區域,只有在每個區域內,位勢為常數;而在區域與區域之間,位勢不相等,則稱此粒子為半自由粒子。自由粒子和半自由粒子的能量大於位勢,
,則這粒子不會被束縛於位勢阱內。因此,在這裏,粒子的量子行為主要是由位勢阱造成的散射(scattering)行為。稱這粒子的量子態為散射態。稱這不被束縛的粒子為自由粒子。更強版的定義還要求位勢為常數。假若,一維空間分為幾個區域,只有在每個區域內,位勢為常數;而在區域與區域之間,位勢不相等,則稱此粒子為半自由粒子。自由粒子和半自由粒子的能量大於位勢, ,不會被束縛於位勢阱內,能量不是離散能量譜的特殊值,而是大於或等於
,不會被束縛於位勢阱內,能量不是離散能量譜的特殊值,而是大於或等於  的任意值。波數
的任意值。波數 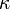 ,用方程式表達為
,用方程式表達為  ,也不是離散量。代入方程 (1) :
,也不是離散量。代入方程 (1) : ,
, 。
。
 ,
, 。
。
 、
、 、
、 、
、 ,都是常數。
,都是常數。


No comments:
Post a Comment