phymath999: tensor01 能量-動量張量(energy-momentum tensor)，在物理學中是一個張量，描述能量與動量在時空中的密度與通量(flux)，其為牛頓物理中應力張量的推廣。在廣義相對論中，其為重力場的源，一如牛頓重力理論中質量是重力場源一般

Tuesday, February 4, 2014

tensor01 能量-動量張量(energy-momentum tensor)，在物理學中是一個張量，描述能量與動量在時空中的密度與通量(flux)，其為牛頓物理中應力張量的推廣。在廣義相對論中，其為重力場的源，一如牛頓重力理論中質量是重力場源一般

能量-動量張量(energy-momentum tensor)，在物理學中是一個張量，描述能量與動量在時空中的密度與通量(flux)，其為牛頓物理中應力張量的推廣。在廣義相對論中，其為重力場的源，一如牛頓重力理論中質量是重力場源一般

應力-能量張量[编辑]

维基百科，自由的百科全书

跳转至：导航、搜索

應力-能量張量(stress-energy tensor)，也稱應力-能量-動量張量(stress-energy-momentum tensor)、能量-應力張量(energy-stress tensor)、能量-動量張量(energy-momentum tensor)，在物理學中是一個張量，描述能量與動量在時空中的密度與通量(flux)，其為牛頓物理中應力張量的推廣。在廣義相對論中，其為重力場的源，一如牛頓重力理論中質量是重力場源一般。應力-能量張量具有重要的應用，尤其是在愛因斯坦場方程式。

定義[编辑]

請注意我們將全程使用到愛因斯坦取和原則。當用到座標表示，x⁰代表時間，其他座標項x¹, x²及x³則為剩下的空間分量。
應力-能量張量為一個二階張量 $T^{ab}$ ，給出四維動量或4-動量之a分量通過一座標為常數x^b之表面的通量。另外要注意的是應力-能量張量是對稱(當自旋張量為零時)，亦即

$T^{ab} = T^{ba} \,$

若自旋張量S非零，則

$\partial_{\alpha}S^{\mu\nu\alpha} = T^{\mu\nu} - T^{\nu\mu}$

例子[编辑]

此處舉出一些特例：

$T^{00}$

代表能量密度。

$T^{0i}$

代表能量通過xⁱ表面之通量，等同於

$T^{i0},$

第i 動量之密度。
分量

$T^{ij}$

代表i 動量通過x^j表面之通量。其中較特別的是：

$T^{ii}$

代表一個類似壓力與張應力的物理量——正向應力(normal stress)，而

$T^{ij}, \quad i \ne j$

代表剪應力(shear stress)。
提醒：在固態物理與流體力學中，應力張量所指為應力-能量張量於共動參考系(comoving frame of reference)的空間分量。換句話說，工程學中的應力-能量張量與此處由動量對流項(momentum convective term)表示的應力-能量張量有所差異。

作為諾特流(Noether current)[编辑]

應力-能量張量滿足連續性方程式(continuity equation)

$\nabla_b T^{ab}=T^{ab}{}_{;b}=0$ .

此一物理量

$\int d^3x T^{a0}$

是對一類空切面積分，得出能量-動量向量。分量 $T^{a0}$ 因此可以詮釋為（非重力的）能量與動量之局域密度，而連續性方程式的第一分量

$\nabla_b T^{0b} = \nabla \cdot \mathbf{p} - \frac{\partial E}{\partial t} = 0$

則單純是能量守恆的表述。空間分量 $T^{ij}$ (i, j = 1, 2, 3)則對應到局域非重力的應力分量，其中包括了壓力。此一張量為與時空移動相應的守恆諾特流(Noether current)。

於廣義相對論中[编辑]

上面所給的關係並不唯一決定此張量。在廣義相對論中，對稱形式的張量，也就是額外滿足

$T^{ab} = T^{ba}$

的關係的張量成為時空曲率的源，並且是與規範变換(gauge transformation)相應的流密度(current density)，在此是以座標变換為例。若有扭率(torsion)，則此張量就不再是對稱的。這對應到非零自旋張量的例子。參見愛因斯坦-嘉當重力。
在廣義相對論中，平直時空所用的偏導數(偏微分，partial derivative)修改為協變導數(covariant derivative)。這表示連續性方程式中用張量表示的能量和動量不是絕對地守恆。在牛頓重力的古典極限，這一點有一個簡單的解釋：與引力位能互相交換的能量，它沒有包含在能動張量中，而動量是通過場傳遞到其他物體。然而在廣義相對論中，無法定義對應「重力場」能量密度與動量密度的物理量；任何意圖要定義這些密度的膺張量(pseudo-tensor)均可以透過一個座標轉換使它們局域地消失為零。一般情況下，對於應力─能量張量只是部分的"協變守恆"，我們必須感到心滿意足。
在彎曲時空中，一般而言類空積分依賴於類空截面。事實上在一般的彎曲時空中是無法定義一個全局的能量─動量張量（原文誤為'vector'）。

愛因斯坦場方程式[编辑]

主条目：愛因斯坦場方程式

在廣義相對論中，應力-能量張量主要出現在愛因斯坦場方程式的研究題材中，方程式常寫為：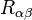

$R_{\alpha \beta} - {1 \over 2}R\,g_{\alpha \beta} = {8 \pi G \over c^4} T_{\alpha \beta},$

其中 $R_{\alpha \beta}$ 為里奇張量, $R$ 為里奇純量（對里奇張量做張量縮併(tensor contraction)而得），以及 $G$ 為宇宙重力常數(universal gravitational constant).

特殊情况下的应力-能量张量[编辑]

孤立粒子[编辑]

在狭义相对论中，质量为m的无相互作用粒子的应力-能量张量为：

$T^{\alpha \beta}[t,x,y,z] = \frac{m \, v^{\alpha}[t] v^{\beta}[t]}{\sqrt{1 - (v/c)^2}} \delta(x - x[t]) \delta(y - y[t]) \delta(z - z[t])$

其中δ是狄拉克δ函数， $v^{\alpha} \!$ 是速度矢量：

$\begin{pmatrix} v^0 [t] \\ v^1 [t] \\ v^2 [t] \\ v^3 [t] \end{pmatrix} = \begin{pmatrix} 1 \\ {d x [t] \over d t} \\ {d y [t] \over d t} \\ {d z [t] \over d t} \end{pmatrix} .$

处于平衡状态下的流体的应力-能量张量[编辑]

对于处于热平衡状态下的流体，应力-能量张量具有一个特别简单的形式：

$T^{\alpha \beta} \, = (\rho + {p \over c^2})u^{\alpha}u^{\beta} + p g^{\alpha \beta}$

其中 $\rho$ 是质量-能量密度（牛顿每立方米）， $p$ 是流体静压力（牛顿每平方米）， $u^{\alpha}$ 是流体的四维速度， $g^{\alpha \beta}$ 是度量张量的逆。
四维速度满足：

$u^{\alpha} u^{\beta} g_{\alpha \beta} = - c^2 \,.$

在随流体一起移动的惯性参考系中，四维速度为：

$u^{\alpha} = (1, 0, 0, 0) \,,$

度量张量的倒数为：

$g^{\alpha \beta} \, = \left( \begin{matrix} - c^{-2} & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right) \,,$

应力-能量张量是一个对角矩阵：

$T^{\alpha \beta} = \left( \begin{matrix} \rho & 0 & 0 & 0 \\ 0 & p & 0 & 0 \\ 0 & 0 & p & 0 \\ 0 & 0 & 0 & p \end{matrix} \right).$

电磁应力-能量张量[编辑]

主条目：电磁应力-能量张量

一个无源电磁场的应力-能量张量为：

$T^{\mu \nu} (x) = \frac{1}{\mu_0} \left( F^{\mu \alpha} g_{\alpha \beta} F^{\nu \beta} - \frac{1}{4} g^{\mu \nu} F_{\delta \gamma} F^{\delta \gamma} \right)$

其中 $F_{\mu \nu}$ 是电磁张量。

标量场[编辑]

主条目：克莱因-戈尔登方程

满足克莱因-戈尔登方程的标量场 $\phi$ 的应力-能量张量为：

$T^{\mu\nu} = \frac{\hbar^2}{m} (g^{\mu \alpha} g^{\nu \beta} + g^{\mu \beta} g^{\nu \alpha} - g^{\mu\nu} g^{\alpha \beta}) \partial_{\alpha}\bar\phi \partial_{\beta}\phi - g^{\mu\nu} m c^2 \bar\phi \phi .$

各式各樣的應力-能量張量[编辑]

存在有一些互不相等的應力-能量張量。

正則(Canonical)應力-能量張量[编辑]

其為與時空平移相關的諾特流。

希爾伯特應力-能量張量[编辑]

應力-能量張量在廣義相對論中僅能以動態度規來定義。其定義成一個泛函導數(functional derivative)

$T^{\mu\nu}(x)=\frac{2}{\sqrt{-g}}\frac{\delta \mathcal{S}_{\mathrm{matter}}}{\delta g_{\mu\nu}(x)}$

其中S_matter是作用量的非重力部份，為對稱的且有規範不變性。

Belinfante-Rosenfeld應力-能量張量[编辑]

赝張量(Pseudotensors)[编辑]

赝張量的例子有愛因斯坦赝張量與藍道-里夫須茲赝張量(Landau-Lifschitz pseudotensor)。

phymath999