聽了今天的課之後,想了一下:
守恆力的大小是否為一個位移的函數(比如說重力為常數mg,彈力為一次函數-kx),故不論運動過程為何,事實上該守恆力與路徑的積分只與初位置與末位置有關,且積分的結果即為該守恆力的位能。
在這樣的前提下,我們以前高中曾說:重力 彈力 靜電力 是保守力 是不是有問題?
我的想法是這樣的:要判斷一個力是否為守恆力應該是要看運動的過程是否力學能守恆,比如說一個帶電粒子以速度v由電位低向電位高前進,當速度為0時,動能全部轉換為電位能,此時力學能守恆。但若此時將外加的電場關閉,剛剛的電位能是否就消失了?此時的靜電力還能稱為"守恆力"嗎?
Show more replies (5 hidden) 守恆力的大小是否為一個位移的函數(比如說重力為常數mg,彈力為一次函數-kx),故不論運動過程為何,事實上該守恆力與路徑的積分只與初位置與末位置有關,且積分的結果即為該守恆力的位能。
在這樣的前提下,我們以前高中曾說:重力 彈力 靜電力 是保守力 是不是有問題?
我的想法是這樣的:要判斷一個力是否為守恆力應該是要看運動的過程是否力學能守恆,比如說一個帶電粒子以速度v由電位低向電位高前進,當速度為0時,動能全部轉換為電位能,此時力學能守恆。但若此時將外加的電場關閉,剛剛的電位能是否就消失了?此時的靜電力還能稱為"守恆力"嗎?
我的意思是:如果在一個運動的過程中,這個力(不管是重力、彈力、或是靜電力)沒辦法再寫成位移的函數,是不是就不能說是保守力了。
比如說在我上面提到的例子裡,一開始有外加電場,因此帶電粒子受到一個不隨位置改變的力可以寫成常數函數F(X)=qE,但我們關閉外加電場後,這個帶電粒子所受的力寫成函數變成F(x)=0,因此在"一整個"過程,把力對位移作圖之後會得出兩條水平線,這樣的圖形不是"函數",在這個情況之下,靜電力是否就不能叫做守恆力。
我的意思是:我們在定義守恆力的時候,應該是要針對"某一個運動的過程"來看"某個力"是不是守恆力,不能因為在大多數的情況下重力 彈力跟靜電力都滿足"力的大小可寫為位移的函數",就說重力 彈力 靜電力是守恆力。
比如說在我上面提到的例子裡,一開始有外加電場,因此帶電粒子受到一個不隨位置改變的力可以寫成常數函數F(X)=qE,但我們關閉外加電場後,這個帶電粒子所受的力寫成函數變成F(x)=0,因此在"一整個"過程,把力對位移作圖之後會得出兩條水平線,這樣的圖形不是"函數",在這個情況之下,靜電力是否就不能叫做守恆力。
我的意思是:我們在定義守恆力的時候,應該是要針對"某一個運動的過程"來看"某個力"是不是守恆力,不能因為在大多數的情況下重力 彈力跟靜電力都滿足"力的大小可寫為位移的函數",就說重力 彈力 靜電力是守恆力。
首先,保守力的定義為環積分:∮Fdx=0
要滿足這個式子的前提是保守力一定要是位移的函數,所以這裡只是要提醒你,可以寫成是位移函數的力未必是保守力。
二者,當我們在探討力學能守恆的時候,我們是在討論”同一個”system下的energy改變。用你的example 來說,假設一個帶電粒子原本是以初速v在均勻電場下運動,又假設這電力的方向相反於原本粒子的運動方向,當粒子v=0時,total energy = potential energy,這時改變電場後,我們已經不是在討論同一個system了,這時total energy的值已經改變,這個觀念其實就在於potential其實是描述場(重力場、電磁場)的方便工具,它並不是一個實際存在的能量(可是動能是,所以才會有功能原理),所以改變場就會改變這個system中的potential分布,這並不代表力學能不守恆,因為這時我們已經在探討兩個不同的system了。
要滿足這個式子的前提是保守力一定要是位移的函數,所以這裡只是要提醒你,可以寫成是位移函數的力未必是保守力。
二者,當我們在探討力學能守恆的時候,我們是在討論”同一個”system下的energy改變。用你的example 來說,假設一個帶電粒子原本是以初速v在均勻電場下運動,又假設這電力的方向相反於原本粒子的運動方向,當粒子v=0時,total energy = potential energy,這時改變電場後,我們已經不是在討論同一個system了,這時total energy的值已經改變,這個觀念其實就在於potential其實是描述場(重力場、電磁場)的方便工具,它並不是一個實際存在的能量(可是動能是,所以才會有功能原理),所以改變場就會改變這個system中的potential分布,這並不代表力學能不守恆,因為這時我們已經在探討兩個不同的system了。
本來并不是很了解守恒力的,但經過昨天的課程后,雖然不知道自己的認知是否正確,但算是有了一些概念~如果要我試著闡述 “一定要有均勻場能量才是守恒” 這個觀念是否正確,我認為一獨立系統,在無非守恆力作用下,其機械能(動能與位能的總和)是守恆的,此稱之為力學能守恆原理;在存在有非守恆力作用下,我們若是把非守恆力作用所產生的熱能、聲能等非力學能都考慮進來的話,總能量還是守恆的。
102023069 黃君平
102023069 黃君平
其實柏翰同學描述的現象,在isolated system中很難發生。電場不會在一瞬間消失,電場消失時一定需要時間,而電場改變的時候會induce磁場,而這個磁場又會再induce一個電場,因而形成電磁波,所以改變場的時候,能量就隨著電磁波傳遞出去了。
均勻場的概念其實就是 在某個固定的位置所受的力永遠不變 就是守恆力的定義耶
所以均勻場一定是守恆力應該是對的吧
但是一定要是均勻場才守恆不知道是不是對的耶??
彈簧也能視為均勻場嗎? 還是彈簧就是一個反例?
isolated system似乎不能和外界有能量和物質交換 改變電場時那個系統是否就不能視為isolated了呢@@?
所以均勻場一定是守恆力應該是對的吧
但是一定要是均勻場才守恆不知道是不是對的耶??
彈簧也能視為均勻場嗎? 還是彈簧就是一個反例?
isolated system似乎不能和外界有能量和物質交換 改變電場時那個系統是否就不能視為isolated了呢@@?
靖雯同學:
從高中場的概念出發(以電場為例),首先假設有一個電荷q在某位置X受到的電力為F,並且假設此電荷不會影響空間中的電場,因此電場便可以定義為F/q,在此定義下場可以說是正比於所受到的力,均勻場顧名思義是各點的場相同,也就是相同物體在各點所受到的力均相同,並不是在某個固定的位置所受的力永遠不變(這是結果不是定義),當然,均勻場為保守力場
在高中應該學過遠地表的重力場,此重力場是不是均勻場呢?它又是不是保守力場呢?
依照剛剛定義的均勻力場,彈簧力場是均勻場嗎?
我不太清楚你提到的那個系統,指的是單單只有粒子本身嗎?還是有包含場呢?
從高中學習場的方式,很容易感覺到場似乎沒什麼用,畢竟是由力來定義場,真的要計算粒子的運動時,還是會回到F=ma來計算,但實際上來說力跟場是以不同的觀點來分析問題,以力的觀點來分析的話,我們必須先寫下系統每個粒子的EOM,接著解出每個粒子的x(t),但是當粒子越來越多的時候,這個方法就會變得非常麻煩且複雜,試想你要處理房間氣體分子的運動狀態,你絕對不會想要寫下全部粒子的運動方程,然後來開始計算的,因此這時就需要一個比較巨觀的看法-場,舉例來說我們可以將房間切成很多尺寸適中的小方格,接著定義每個方格裡面的粒子密度,分析每個方格的密度隨時間的變化,我們就可以知道房間裡的氣體分子平均來說怎麼運動的,這就是場的分析方法。
助教 威廷
势能零点可任意取
势能[编辑]
势能(Potential Energy),亦稱位能,是储存于一物理系统内的一种能量,是一个用来描述物体在保守力场中做功能力大小的物理量。保守力作功与路径无关,故可定义一个仅与位置有关的函数,使得保守力沿任意路径所做的功,可表达为这两点对应函数值的差,这个函数便是势能。
从物理意义上来说,势能表示了物体在特定位置上所储存的能量,描述了作功能力的大小。在适当的情况下,势能可以转化为诸如动能、内能等其他能量。
除此之外,我们还可以将势能的定义从现在的基础上拓展。比如热学中气体分子间的相互作用势能,它是大量分子势能的和,实际不是用相对位置(位形)来描述的,而是用体积、温度、压强等热学参量。又如,在一些特定的约束条件下,某些平时是非保守力的力也成为了保守力[3],或者几种力的合力恰巧成为了一个保守力。如此种种。
广义势能最主要的应用在于带电粒子在电磁场中的运动上。带有电荷q,以速度v移動的粒子在电场E和磁场B中受到洛伦兹力
势能是一个标量函数,当一个物体与多个物体共有势能或共有多种势能时,这个物体所具有的总势能为所有势能的代数和。
由定义可知,势能取决于两个或多个物体的相对位形,是两个或多个物体所共有的。然而,在两物体A、B组成的保守体系中,如果我们以其中一个物体A作为参考系,则势能仅取决于另一物体B的相对位置。这时,在不引起混淆的情况下,我们常把“A、B具有的势能”称作是“B的势能”。比如,在电场中的电荷具有静电势能,或者是在一个天体附近的另一个天体具有引力势能。除此之外,有时候保守体系中只存在一个物体,势能来自于物体内部各部分间的相对位移,这时候我们也说,势能是这个物体所具有的。比如,弹簧,或者是具有体分布电荷的绝缘体球。
需要注意的是,即使在同一保守力场中的同一处,不同物体的势能也一般不同,比如在重力作用范围内,物体的重力势能不仅取决于其高度,还取决于其质量。
具有更多势能的物体有能力对外界作出更多的功,用非保守力对物体做功也可以使之获得更多的势能。[8]故,当物体在保守力的作用下(但不一定仅受保守力)从a处沿任意路径移动到b处时,总势能变化量为保守力作功的相反值,即
势能为保守力关于位移的积分,相对地,保守力为相应势能函数关于位移的负梯度,即
 为外力作功,
为外力作功, 为非保守内力作功。若
为非保守内力作功。若 ,
, ,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。
,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。
在构建理想模型时,机械能守恒定律应用得十分广泛,特别是当一质点处在有心力场时,其机械能守恒;又因为动能Ek>0,在已知总能量的情况下,可以了解到质点理论上的行动范围(满足Ek<E的区域)。
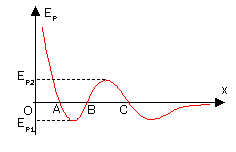
设在x方向上有如图势能曲线,则我们把AB间势能最低处叫作势阱(C右方也有一个势阱),BC间势能最高处叫作势垒,对应的有势阱深度与势垒高度。我们设定粒子机械能守恒,那么:
假設一个粒子从无穷远处靠近,其机械能为E=0,那么在C点处其动能为零,再向左走动能为负,速度将为虚数,经典力学中这是不允许的。因此它最多只能到达C处。随着粒子机械能(即初动能)的增大,其运动范围的左端将会延伸,当其机械能达到或超过Ep2时,它将可以翻过势垒。
再假设一个粒子,初始时在AB间。若它机械能为0,那么它可以在AB间运动,其最大动能为Ek max=Ep1。当其机械能不断增大,达到Ep2时,它将可以翻越势垒,到达B右方空间(当然,其在A左方的空间也会延伸)。
势能图、势垒等概念是讨论单个质点在保守外场中运动的有力工具,在物理学多个领域中的应用都十分广泛。[10]
 ,则称物体处于平衡。右图A、B、C三点皆处于平衡。
,则称物体处于平衡。右图A、B、C三点皆处于平衡。
当物体偏离平衡位置时,若受合力背向平衡位置,则物体有离开平衡位置的趋势,则称物体处于不稳定平衡。势能曲线上,不稳定平衡即满足 的点。右图A点处于不稳定平衡。
的点。右图A点处于不稳定平衡。
当物体偏离平衡位置时,若受合力指向平衡位置,则物体有回到平衡位置的趋势,则称物体处于稳定平衡。势能曲线上,稳定平衡即满足 的点。右图B点处于稳定平衡。
的点。右图B点处于稳定平衡。
当物体在平衡位置附近时合力恒为零,则称物体处于随遇平衡。势能曲线上,随遇平衡即满足 的点。右图C点处于随遇平衡。
的点。右图C点处于随遇平衡。
以上只是一种粗略的分析方法,实际上,在二维或高维空间中情况会更加复杂,比如,在不同的方向上具有不同的平衡种类[11]。一个最简单的例子是,若物体被约束在马鞍形势能曲面上,位于中心时,在x方向上为稳定平衡,在y方向上为不稳定平衡。
需要与势能区分开的是,物体并不一定总是向势更低的地方运动。一个正电荷会趋向于达到电势更低的地方,但一个负电荷会趋向于达到电势更高的地方,但那里都分别是它们势能更低处。
势也包括一些势能所不包括的内容,如磁矢势。
在下面的介绍中,我们常考虑一个两质点组成的保守体系,两质点间受且仅受相应的一种保守力。两质点的势能是一种最简单、最理想的模型,然而也是实际模型的基础。实际的问题理论上都可以由两质点势能的函数加以积分得到。
在这种情况下,重力大致[15]只与星体性质与物体质量有关,而与位置无关,方向铅直向下[16]。将重力加速度定为常数g,则物体重力大小为
重力势能并没有严格的势能零点定义,完全依计算方便而定,不过比较常用的是以地面或桌面为势能零点。
在地球上g的值约为9.8 ms-2,在不同地区稍有不同。这个值已经包括了和地球自转所需的向心力造成的差别。一般计算中g可近似的取作标准重力加速度,即g=gn=9.80665 ms-2 [17]。
对兰纳-琼斯势在排斥力部分简化,成为苏则朗势(Sutherland potential),即
对苏则朗势在引力部分再次简化,成为刚球势,即
從高中場的概念出發(以電場為例),首先假設有一個電荷q在某位置X受到的電力為F,並且假設此電荷不會影響空間中的電場,因此電場便可以定義為F/q,在此定義下場可以說是正比於所受到的力,均勻場顧名思義是各點的場相同,也就是相同物體在各點所受到的力均相同,並不是在某個固定的位置所受的力永遠不變(這是結果不是定義),當然,均勻場為保守力場
在高中應該學過遠地表的重力場,此重力場是不是均勻場呢?它又是不是保守力場呢?
依照剛剛定義的均勻力場,彈簧力場是均勻場嗎?
我不太清楚你提到的那個系統,指的是單單只有粒子本身嗎?還是有包含場呢?
從高中學習場的方式,很容易感覺到場似乎沒什麼用,畢竟是由力來定義場,真的要計算粒子的運動時,還是會回到F=ma來計算,但實際上來說力跟場是以不同的觀點來分析問題,以力的觀點來分析的話,我們必須先寫下系統每個粒子的EOM,接著解出每個粒子的x(t),但是當粒子越來越多的時候,這個方法就會變得非常麻煩且複雜,試想你要處理房間氣體分子的運動狀態,你絕對不會想要寫下全部粒子的運動方程,然後來開始計算的,因此這時就需要一個比較巨觀的看法-場,舉例來說我們可以將房間切成很多尺寸適中的小方格,接著定義每個方格裡面的粒子密度,分析每個方格的密度隨時間的變化,我們就可以知道房間裡的氣體分子平均來說怎麼運動的,這就是場的分析方法。
助教 威廷
势能零点可任意取
势能[编辑]
维基百科,自由的百科全书
从物理意义上来说,势能表示了物体在特定位置上所储存的能量,描述了作功能力的大小。在适当的情况下,势能可以转化为诸如动能、内能等其他能量。
目录
[隐藏]势能[编辑]
势能的保守力定义[编辑]
如果分别作用于两个质点上的作用力与反作用力作功与具体路径无关,只取决于相互作用质点初末位置,那么这样的一对力就叫作保守力。不满足这个条件的则称为非保守力。可以证明保守场的几个等价条件[1],于是我们得到保守力的性质有:- 保守力沿给定两点间作功与路径无关;
- 保守力沿任意环路作功为零;
- 保守力可以表示为一个标量函数的(负)梯度;
除此之外,我们还可以将势能的定义从现在的基础上拓展。比如热学中气体分子间的相互作用势能,它是大量分子势能的和,实际不是用相对位置(位形)来描述的,而是用体积、温度、压强等热学参量。又如,在一些特定的约束条件下,某些平时是非保守力的力也成为了保守力[3],或者几种力的合力恰巧成为了一个保守力。如此种种。
广义势能[编辑]
对于一个理想、完整体系,有拉格朗日方程广义势能最主要的应用在于带电粒子在电磁场中的运动上。带有电荷q,以速度v移動的粒子在电场E和磁场B中受到洛伦兹力
势能的性质[编辑]
势能为能量的一种,具有能量量纲,在国际单位制下的单位是焦耳(J),另外在涉及到粒子物理时常用到电子伏特(eV),高斯单位制下为尔格(erg)。势能一般使用“Ep”[2]表示,也常使用“W”[6]“U”和“V”[7]。势能是一个标量函数,当一个物体与多个物体共有势能或共有多种势能时,这个物体所具有的总势能为所有势能的代数和。
由定义可知,势能取决于两个或多个物体的相对位形,是两个或多个物体所共有的。然而,在两物体A、B组成的保守体系中,如果我们以其中一个物体A作为参考系,则势能仅取决于另一物体B的相对位置。这时,在不引起混淆的情况下,我们常把“A、B具有的势能”称作是“B的势能”。比如,在电场中的电荷具有静电势能,或者是在一个天体附近的另一个天体具有引力势能。除此之外,有时候保守体系中只存在一个物体,势能来自于物体内部各部分间的相对位移,这时候我们也说,势能是这个物体所具有的。比如,弹簧,或者是具有体分布电荷的绝缘体球。
需要注意的是,即使在同一保守力场中的同一处,不同物体的势能也一般不同,比如在重力作用范围内,物体的重力势能不仅取决于其高度,还取决于其质量。
势能物理意义[编辑]
当物体从高势能处来到低势能处时,该物体势能减少,而保守力向外作等量功使其它某种能量增加。从中我们可以发现,势能可以表示一个物体所储存的能量的多少。如,放在高处的物体相比放在放在低处的物体而言具有更多的重力势能,当它从空中向下坠落的时候,重力势能减少,转化为动能;而当它沿粗糙斜面下滑时,重力势能同时转化为动能和内能。具有更多势能的物体有能力对外界作出更多的功,用非保守力对物体做功也可以使之获得更多的势能。[8]故,当物体在保守力的作用下(但不一定仅受保守力)从a处沿任意路径移动到b处时,总势能变化量为保守力作功的相反值,即
势能为保守力关于位移的积分,相对地,保守力为相应势能函数关于位移的负梯度,即
机械能[编辑]
势能Ep与动能Ek之和称为机械能。 为外力作功,
为外力作功, 为非保守内力作功。若
为非保守内力作功。若 ,
, ,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。
,则质点系机械能守恒,这就是机械能守恒定律。这时,质点系与外界无能量交换,内部也无机械能与非机械能的转化,只有动能与势能的相互转换。在构建理想模型时,机械能守恒定律应用得十分广泛,特别是当一质点处在有心力场时,其机械能守恒;又因为动能Ek>0,在已知总能量的情况下,可以了解到质点理论上的行动范围(满足Ek<E的区域)。
设在x方向上有如图势能曲线,则我们把AB间势能最低处叫作势阱(C右方也有一个势阱),BC间势能最高处叫作势垒,对应的有势阱深度与势垒高度。我们设定粒子机械能守恒,那么:
假設一个粒子从无穷远处靠近,其机械能为E=0,那么在C点处其动能为零,再向左走动能为负,速度将为虚数,经典力学中这是不允许的。因此它最多只能到达C处。随着粒子机械能(即初动能)的增大,其运动范围的左端将会延伸,当其机械能达到或超过Ep2时,它将可以翻过势垒。
再假设一个粒子,初始时在AB间。若它机械能为0,那么它可以在AB间运动,其最大动能为Ek max=Ep1。当其机械能不断增大,达到Ep2时,它将可以翻越势垒,到达B右方空间(当然,其在A左方的空间也会延伸)。
势能图、势垒等概念是讨论单个质点在保守外场中运动的有力工具,在物理学多个领域中的应用都十分广泛。[10]
物体在势能场中的平衡[编辑]
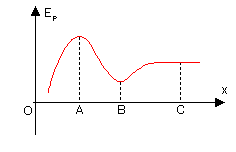
只受保守力作用的物体,总有向总势能更低处运动的趋势。当物体所处位置不受力作用或合力为零时,即 ,则称物体处于平衡。右图A、B、C三点皆处于平衡。
,则称物体处于平衡。右图A、B、C三点皆处于平衡。当物体偏离平衡位置时,若受合力背向平衡位置,则物体有离开平衡位置的趋势,则称物体处于不稳定平衡。势能曲线上,不稳定平衡即满足
 的点。右图A点处于不稳定平衡。
的点。右图A点处于不稳定平衡。当物体偏离平衡位置时,若受合力指向平衡位置,则物体有回到平衡位置的趋势,则称物体处于稳定平衡。势能曲线上,稳定平衡即满足
 的点。右图B点处于稳定平衡。
的点。右图B点处于稳定平衡。当物体在平衡位置附近时合力恒为零,则称物体处于随遇平衡。势能曲线上,随遇平衡即满足
 的点。右图C点处于随遇平衡。
的点。右图C点处于随遇平衡。以上只是一种粗略的分析方法,实际上,在二维或高维空间中情况会更加复杂,比如,在不同的方向上具有不同的平衡种类[11]。一个最简单的例子是,若物体被约束在马鞍形势能曲面上,位于中心时,在x方向上为稳定平衡,在y方向上为不稳定平衡。
势[编辑]
在物理中有时会提到势,请不要与势能相混淆。势通常表述为势能与一个物理量的比值,如电势(一个粒子静电势能与其电荷量的比值),引力势(一个物体引力势能与其质量的比值)。一个确定保守力场中,一个物体的势能与该物体有关,但势的分布与该物体无关[12]。需要与势能区分开的是,物体并不一定总是向势更低的地方运动。一个正电荷会趋向于达到电势更低的地方,但一个负电荷会趋向于达到电势更高的地方,但那里都分别是它们势能更低处。
势也包括一些势能所不包括的内容,如磁矢势。
几种常见势能[编辑]
下面介绍几种常见势能。在下面的介绍中,我们常考虑一个两质点组成的保守体系,两质点间受且仅受相应的一种保守力。两质点的势能是一种最简单、最理想的模型,然而也是实际模型的基础。实际的问题理论上都可以由两质点势能的函数加以积分得到。
引力势能[编辑]
- 注意:在臺湾或其他地区[來源請求]将万有引力统称为“重力”,然而在大陆地区将万有引力称作“引力”,而将“重力”作为万有引力的一种特殊简化情形。这里为了分别介绍两种情况,不致混淆,暂采用大陆命名方法。
重力势能[编辑]
重力势能是引力势能在一种特殊情况下的简化形式。可以证明[13],对一球对称分布物体在其外一质点产生的引力,上面两质点间的作用力公式仍适用,其中m0为该物体总质量,r0为其球心位矢。当 |r-r0| 在不太大范围内变动时,对作用力公式取零级近似,作用力不变,则引力退化为重力。[14]由此可见,重力的近似要求很严格。然而由于在日常生活中这个条件很容易满足,而且极简便,符合人们的日常生活经验,故仍有研究价值,单列一项。在这种情况下,重力大致[15]只与星体性质与物体质量有关,而与位置无关,方向铅直向下[16]。将重力加速度定为常数g,则物体重力大小为
 。
。
重力势能并没有严格的势能零点定义,完全依计算方便而定,不过比较常用的是以地面或桌面为势能零点。
在地球上g的值约为9.8 ms-2,在不同地区稍有不同。这个值已经包括了和地球自转所需的向心力造成的差别。一般计算中g可近似的取作标准重力加速度,即g=gn=9.80665 ms-2 [17]。
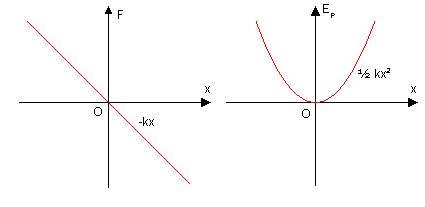
弹性势能[编辑]
弹簧、钢片、金属丝等满足胡克定律的物体,在弹性限度内应力与应变成正比。下面以弹簧为例。在弹性限度内,弹簧弹力与长度变化量的关系为电势能[编辑]
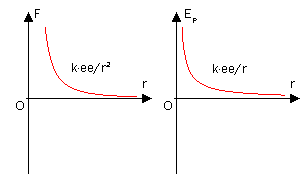
在靜電學裏,根据库伦定律,对于两静止点电荷q、q0,点电荷q受到的静电力为 。
。
分子势能[编辑]
分子力实际上来源于多个方面,精确的计算与各分子内部结构有很大关系,会变得十分复杂。对于无极性分子,两分子间作用力可近似用以下半经验公式表示:[19]- 在某一个值r0以内,分子里表现为排斥力并且随r减小而急剧上升;
- 在r0以外表现为牽引力,分子力逐渐增大,到某最大值后减小;
- 力程短,在r约为r0十倍时已几乎为零。
对兰纳-琼斯势在排斥力部分简化,成为苏则朗势(Sutherland potential),即
对苏则朗势在引力部分再次简化,成为刚球势,即
































![E_p(r)=E_{p0} \left[ \left( \frac{r_0}{r}\right)^{12} - 2\left(\frac{r_0}{r} \right) ^6 \right]](http://upload.wikimedia.org/math/c/1/3/c13ffeb3dc1c6fd6a07711e7aeadd0ad.png)



No comments:
Post a Comment