Sunday, February 9, 2014

Quadratic Equations mathsisfun.com

Quadratic Equations

An example of a Quadratic Equation: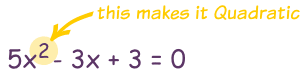

The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x²).
It is also called an "Equation of Degree 2" (because of the "2" on the x)

The Standard Form of a Quadratic Equation looks like this:

a, b and c are known values. a can't be 0.

"x" is the variable or unknown (you don't know it yet).

Here are some more examples:

		In this one a=2, b=5 and c=3

		This one is a little more tricky: Where is a? In fact a=1, as we don't usually write "1x²" b = -3 And where is c? Well, c=0, so is not shown.
		Oops! This one is not a quadratic equation, because it is missing x² (in other words a=0, and that means it can't be quadratic)

Hidden Quadratic Equations!

So the "Standard Form" of a Quadratic Equation is

ax² + bx + c = 0

But sometimes a quadratic equation doesn't look like that! For example:

In disguise	→	In Standard Form	a, b and c
x² = 3x -1	Move all terms to left hand side	x² - 3x + 1 = 0	a=1, b=-3, c=1
2(w² - 2w) = 5	Expand (undo the brackets), and move 5 to left	2w² - 4w - 5 = 0	a=2, b=-4, c=-5
z(z-1) = 3	Expand, and move 3 to left	z² - z - 3 = 0	a=1, b=-1, c=-3
5 + 1/x - 1/x² = 0	Multiply by x²	5x² + x - 1 = 0	a=5, b=1, c=-1

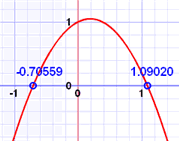Have a Play With It

I have a "Quadratic Equation Explorer" so you can see:

the graph it makes, and
the solutions (called "roots").

How To Solve It?

The "solutions" to the Quadratic Equation are where it is equal to zero. There are usually 2 solutions (as shown in the graph above).
They are also called "roots", or sometimes "zeros"

There are 3 ways to find the solutions:

1. You can Factor the Quadratic (find what to multiply to make the Quadratic Equation)

2. You can Complete the Square, or

3. You can use the special Quadratic Formula:

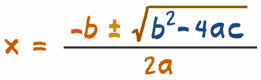
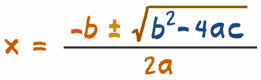
Just plug in the values of a, b and c, and do the calculations.

We will look at this method in more detail now.

About the Quadratic Formula

Plus/Minus

First of all what is that plus/minus thing that looks like ± ?

The ± means there are TWO answers: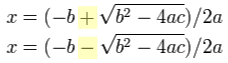

Here you see why you can get two answers:

But sometimes you don't get two real answers, and the "Discriminant" shows why ...

Discriminant

Do you see b² - 4ac in the formula above? It is called the Discriminant, because it can "discriminate" between the possible types of answer:

when b² - 4ac is positive, you get two Real solutions

when it is zero you get just ONE real solution (both answers are the same)

when it is negative you get two Complex solutions

I will explain about Complex solutions after you have seen how to use the formula.

Using the Quadratic Formula

Just put the values of a, b and c into the Quadratic Formula, and do the calculations.

Example: Solve 5x² + 6x + 1 = 0

Coefficients are:		a = 5, b = 6, c = 1

Quadratic Formula:		x = [ -b ± √(b²-4ac) ] / 2a

Put in a, b and c:		x = [ -6 ± √(6²-4×5×1) ] / (2×5)

Solve:		x = [ -6 ± √(36-20) ]/10
		x = [ -6 ± √(16) ]/10
		x = ( -6 ± 4 )/10
		x = -0.2 or -1

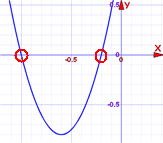Answer: x = -0.2 or x = -1

And you can see them on this graph.

Check -0.2:	5×(-0.2)² + 6×(-0.2) + 1 = 5×(0.04) + 6×(-0.2) + 1 = 0.2 -1.2 + 1 = 0
Check -1:	5×(-1)² + 6×(-1) + 1 = 5×(1) + 6×(-1) + 1 = 5 - 6 + 1 = 0

Remembering The Formula

I don't know of an easy way to remember the Quadratic Formula, but a kind reader suggested singing it to "Pop Goes the Weasel":

♫	"x equals minus b	♫	"All around the mulberry bush
♫	*plus or minus the square root*	♫	The monkey chased the weasel
	*of b-squared minus four a c*		The monkey thought 'twas all in fun
	*all over two a"*		Pop! goes the weasel"

Try singing it a few times and it will get stuck in your head!

Complex Solutions?

When the Discriminant (the value b² - 4ac) is negative you get Complex solutions ... what does that mean?
It means your answer will include Imaginary Numbers. Wow!

Example: Solve 5x² + 2x + 1 = 0

Coefficients are:		a = 5, b = 2, c = 1

Note that The Discriminant is negative:		b² - 4ac = 2² - 4×5×1 = -16

Use the Quadratic Formula:		x = [ -2 ± √(-16) ] / 10

The square root of -16 is 4i (i is √-1, read Imaginary Numbers to find out more)

So:		x = ( -2 ± 4i )/10

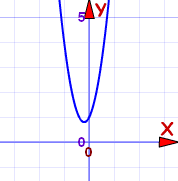Answer: x = -0.2 ± 0.4i

The graph does not cross the x-axis. That is why we ended up with complex numbers.

In some ways it is actually easier ... you don't have to calculate the solutions, just leave it as -0.2 ± 0.4i.

Summary

Quadratic Equation in Standard Form: ax² + bx + c = 0

Quadratic Equations can be factored

Quadratic Formula: x = [ -b ± √(b²-4ac) ] / 2a

When the Discriminant (b²-4ac) is:

positive, there are 2 real solutions
zero, there is one real solution
negative, there are 2 complex solutions

Question 1 Question 2 Question 3 Question 4 Question 5 Question 6 Question 7 Question 8 Question 9 Question 10
(Hard Questions: 1 2 3 4 5 6 7 8 )

phymath999

Sunday, February 9, 2014