维基百科，自由的百科全书
在日常生活中，速率常常和速度混用，但两者在物理学中对应着不同的概念。速率是一个标量，只有大小，没有方向。它的量纲是长度除以时间。速度的量纲和速率相同，但速度是有方向的向量[1]。物体的瞬时速率等于瞬时速度的大小，而平均速率则不一定等于平均速度的大小。在日常生活中，也用“速度”这个词表示速率的意思。
国际单位制中，速率的單位為米每秒（m/s），但日常生活中較常用的單位是千米每小時（km/hr）或是英制系統下的英里每小時（mph）。海上船只或物体的行進速率，一般會使用節作為單位。
依照狭义相对论，能量或信息所能傳遞的最快速率為真空中的光速c = 299,792,458 米每秒，大約是1,079,000,000千米每小时或671,000,000英里每小時。静止质量不为零的物質要加速到此速率，需要無限大的能量。在相對論物理學中，會用快度來取代古典力學中的速度[2]。
定義[编辑]
用数学语言来描述，如果一个物体在一段时间
内移动的路程为
，那么它的平均速率（用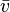
表示）便是与的比，具体可由下式给出：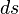
与这段时间长度
的比：
是一个关于时间
的函数，那么物体在某个时刻
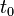的瞬时速率，是以上比值在趋向于0时的极限值。或者说，是在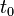时刻对时间的导数。
可能不等于其之后的速率 
：
物体的瞬时速率等于其瞬时速度的大小。然而，物体的平均速率一般不等于其平均速度的大小[3]。盖因路程和位移的概念不同。例如一个物体做匀速圆周运动一周，则其平均速率为一个不为零的定值，但其平均速度是0。
例子[编辑]
瞬時速率[编辑]
車輛上的速度表可以顯示任何时刻的瞬時速率[4]p.42。瞬時速率可能會隨時間而變動，一辆車在某个时刻的瞬時速率50公里/小時，但它維持此速率的時間可以是一秒、一分钟或一小时。不过假若此车連續一小時以50公里/小時的（瞬时）速率行驶，則它所走路程為50公里。平均速率[编辑]
如果一辆車在一小時內行驶了80公里，則它在这一个小时中的平均速率為80公里/小時；若一辆車在第一个小時內行驶了140公里，在接下来的三个小时中行驶了180公里，則它在这四小时内的平均速率也是80公里/小時。但若分别考慮此車第一个小時以及其后三个小時内的平均速率，其數值就不是80公里/小時了。平均速率可能會和過程中的瞬時速率有相當的差異[4]p.42。若已知平均速率和時間，可以求得這段時間所走的路程：
若以圖像的方式，可以利用路程－時間圖来显示速率。路程－時間圖上的曲线表示了物体移动的路程是如何随时间变化的。曲线上任意一點对应着一个时刻和物体在这一时刻移动的路程。曲线在一点上切線的斜率即為此时刻的瞬時速率，而曲线上两點的割线斜率即為对应的二个时刻之間的平均速率。
切線速率[编辑]
物体在单位时间内经历的路程，是为速率或线速率，而如果物体在做圆周运动，那么它的速率也称为切线速率[4]p.131，因为它运动的方向是沿着圆周的切线方向。旋转木马转一圈时，位置靠外的木马走过的路程比位置靠内的木马要多。这说明位置靠外的木马平均速率比位置靠内的木马要大。 對於圓周運動的物體而言，切線速率及線速率二者可互換使用，二者的單位均為m/s或km/h。轉速或角速率是指單位時間内轉的圈數。旋转木马中，不同位置的木马切線速率可能不同，但所有木马在相同時間內都旋轉了相同的圈數，因此其角速率均相同。轉速一般以每分鐘轉速或是以單位時間的弧度作为单位。旋轉一圈的弧度略大於6個弧度（精確值為
弧度）。若將角速率加上方向，則成為角速度，前者為一純量，後者則為一向量。若两片CD每秒都旋轉20圈，一片順時針旋轉，另一片逆時針旋轉，那么二者的角速率相同，但角速度不同。圆周运动的物体（或距旋轉軸固定距離的一點），其切線速率和轉速成正比[4]p.131。不過切線速率和轉速不同，一點的切線速率和距旋轉軸的距離有關，距旋轉軸不同距離的二點，其轉速相等，但切线速率不相等。旋轉軸上的点，其切線速率甚至為零。在一旋轉的物體上，離旋轉軸越遠，會發現线速率越快。若轉速固定，则切線速率和一點距旋轉軸的距離成正比[4]p.132，因此可得下式：
- v為切線速率
- ω為轉速
- r為距旋轉軸的距離
若切線速率、轉速及距離選擇適當的單位（例如切線速率單位選擇m/s，轉速單位選擇弧度/s，距離單位選擇ｍ），上式的比例關係可以變成以下的等式：
No comments:
Post a Comment