Electric quadrupole [edit]

Contour plot of the equipotential surfaces of an electric quadrupole field.

The simplest example of an electric quadrupole consists of alternating positive and negative charges, arranged on the corners of a square. The monopole moment (just the total charge) of this arrangement is zero. Similarly, the dipole moment is zero, regardless to the coordinate origin that has been chosen. But the quadrupole moment of the arrangement in the diagram cannot be reduced to zero, regardless of where we place the coordinate origin. The electric potential of an electric charge quadrupole is given by ^[2]

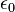$V_q(\mathbf{R})=\frac{1}{4\pi \epsilon_0} \frac{1}{|\mathbf{R}|^3} \sum_{i,j} Q_{ij}\, n_i n_j\ ,$

where $\epsilon_0$ is the electric permittivity.

Electric Quadrupole

A general distribution of electric charge may be characterized by its net charge, by its dipole moment, its quadrupole moment and higher order moments. An elementary quadrupole can be represented as two dipoles oriented antiparallel.

One of the most common uses of the electric quadrupole is in the characterization of nuclei. The nucleus has charge, but not dipole moment since it is all positive. But if the nucleus is not spherically symmetric, it will have a quadrupole moment.
Quadrupole and higher order multipoles are not important for the characteriztion of dielectric materials. Dipole fields are much smaller than the fields of isolated charges, but in dielectrics where there are no free charges, the dipole effects are dominant. There is no such circumstance favoring the quadrupole effects, since they must arise from the same number of molecules as the dipole effects. Scott says that the macroscopic quadrupole effects are smaller than dipole effects by about the ratio of atomic dimensions to the distances of experimental observation.

Field of a linear electric quadrupole

Quadrupole moments of nuclei

Index

Electric dipole concepts

References
Cohen
Concepts of Nuclear Physics, Ch 1

Scott
Sec 3.3

HyperPhysics***** Electricity and Magnetism

R Nave

Go Back

Linear Electric Quadrupole

A linear electric quadrupole can be created by superimposing two electric dipoles of opposite orientation so that their positive charges overlap. This case can be treated analytically and gives some insights into the nature of quadrupole fields. The electric field from any collection of charges can be obtained from Coulomb's law by vector addition of the fields from the individual charge elements.

This has shown that the distant electric field perpendicular to the quadrupole drops off like 1/r⁴. This 1/r⁴ dependence applies to other directions as well. In fact, it is characteristic of quadrupoles in general, although we have not shown that here. It is also a general characteristic of quadrupoles that the electric field depends upon the magnitude of one of the charges times the square of the dimension of the quadrupole, qd².

Binomial expansion

Index

Electric dipole concepts

Reference
Schwarz
Sec 1.4

HyperPhysics***** Electricity and Magnetism

R Nave

Go Back